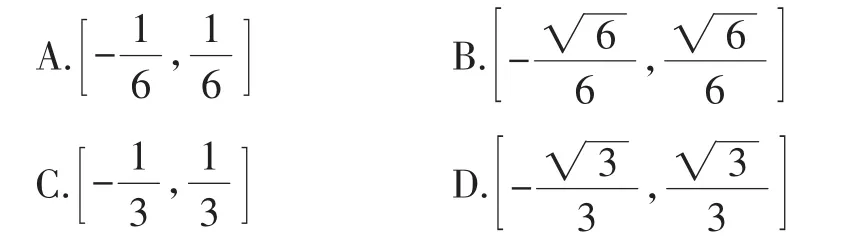正视函数应用中的几个易错问题——以函数的单调性为例

☉浙江省宁波鄞州高级中学 叶琪飞

正视函数应用中的几个易错问题
——以函数的单调性为例

☉浙江省宁波鄞州高级中学 叶琪飞

函数性质是高考对函数考查的主要内容，其中主要涉及函数的单调性、奇偶性、周期性、对称性、零点等.考生在解答此类问题时由于对性质的把握不准确，易陷入解题误区.本文以函数的单调性为例，就其中常见误区举例分析.

一、定义域优先原则

定义域是函数的两个要素之一，函数的性质也是在定义域范围内的性质，因此在涉及单调性相关问题的解答中勿忽视对函数定义域的考虑.

解析：由复合函数的单调性知g（x）=x2-2mx+3在区间（-∞，1）内为减函数，函数g（x）的对称轴为x=m，所以m≥1.又由对数函数的真数大于0，故应有g（1）≥0，即4-2m≥0，解得m≤2，所以实数m的取值范围为［1，2］.

评注：复合函数y=f［g（x）］单调性的处理原则，当f（x）与g（x）的单调性相同时，y=f［g（x）］为增，当f（x）与g（x）的单调性相异时，y=f［g（x）］为减.本题的解答中易忽视对函数定义域的考虑，即函数在区间（-∞，1）上应有x2-2mx+3>0.

A.（0，＋∞）B.（-∞，0）C.（2，＋∞）D.（-∞，-2）

答案：D.

二、准确认识“单调区间”与“在区间上单调”

函数f（x）的“单调区间是D”与“在区间D上单调”的含义，这是两个不同的范围.函数的单调递减区间是I，指的是函数递减的最大范围为区间I，而函数在某一区间上单调递减，则指此区间是相应单调递减区间的子集.

例2若函数f（x）=x2+2（a-1）x+4的单调递减区间是（-∞，4］，则实数a的取值为________.

解析：因为函数的单调递减区间为（-∞，4］，且函数图像的对称轴为直线x＝1-a，所以1-a＝4，即a＝-3.

评注：正确理解“单调区间”和“在区间上单调”的含义，函数的单调区间是函数单调的最大范围，而函数在某一区间上单调，则此区间是相应单调区间的子集.

变式：若函数f（x）=x2+2（a-1）x+4在区间（-∞，4］上单调递减，则实数a的取值范围为________.

答案：（-∞，-3］.

三、函数的单调性是函数的整体性质

函数的单调性是函数的整体性质，若f（x）在区间（-∞，0），［0，+∞）上均为单调增函数，但在（-∞，+∞）内不一定为增.如反比例函数等.

解析：由已知f（x）是（-∞，+∞）上的减函数，应满足如下条件：（1）g1（x）=（3a-1）x+4a在（-∞，1）内单调递减，即3a-1<0，；（2）g2（x）=logax在［1，+∞）内单调递减，所以0

评注：上述解答中易忽视对条件（3）的考虑，即g1（1）≥g2（1），7a-1≥0，a≥

函数的单调性是函数的整体性质，分段函数的单调性问题，在保证左右分支分别满足单调的前提下，应保证在定义域范围内单调性的连续性，即在分段点处的单调性.

A.充分而不必要条件B.必要而不充分条件

C.充分必要条件D.既不充分也不必要条件

答案：B.

四、奇偶函数在对称区间内单调性的异同

偶函数是特殊的对称函数，其关于y轴对称，且在对称两区间内单调性相异.奇函数关于原点对称，且在对称两区间内单调性相同.

例4（2015年新课标卷）设函数f（x）=ln（1+|x|）-则使得f（x）＞f（2x-1）成立的x的取值范围是（）.

评注：若函数f（x）的定义域关于O对称，且在其定义域范围内满足f（-x）=f（x），则f（x）为偶函数，且有f（-x）= f（x）=f（|x|），据此可将不确定区间内的变量范围变换到确定的单调区间内，进而得出变量的范围.

变式：已知函数f（x）是定义在R上的偶函数，且在区间［0，+∞）上单调递增.若实数a满足f（log2a）2f（1），则a的取值范围是_________.

五、f（x+1）>f（x）与f（x）为单调递增函数的关系

图1

若函数f（x）的定义域为R，则“∀x∈R，f（x+ 1）>f（x）”并不能保证“函数f（x）在R内为增函数”，如函数f（x）的图像，如图1，则当a<1时，满足f（x+1）>f（x），但此时f（x）为非单调函数.但当f（x）为单调增函数时，则有f（x+1）>f（x），故“∀x∈R，f（x+1）> f（x）”是“函数f（x）在R内为增函数”的必要非充分条件.

例5（2014年湖北卷）已知函数f（x）是定义在R上的奇函数，当x≥0时（|x-a2|＋|x-2a2|-3a2）.若则实数a的取值范围为（）.

图2

评注：解答本题时需要正确认识“∀x∈R，f（x-1）≤f（x）”，即使f（x）最小时条件成立，进而求出参数的范围.

变式：已知定义域为R的函数f（x）是奇函数，当x≥0时，f（x）=|x-a2|-a2，且对x∈R，恒有f（x+1）≥f（x），则实数a的取值范围为（）.

综上，函数是高中数学的重点和难点，函数性质是函数问题的一条主线，由于这一部分内容具有较强的抽象性，常因缺乏透彻的理解，而出现错解.为了避免错误的重演，错过之后的反思就显得非常重要，因此学习中要善于归纳易错点，分析错因，加强训练，方能取得好的效果.