数学史选修课开课模式与评价标准研究

☉浙江临安天目高级中学 汤丽芬

☉浙江临安天目高级中学 赵国胜

数学史选修课开课模式与评价标准研究

☉浙江临安天目高级中学 汤丽芬

☉浙江临安天目高级中学 赵国胜

“在大多数的学科里，一代人的建筑为下一代人所摧毁，一个人的创造被另一个人所破坏.惟独数学，每一代人都在古老的数学大厦上添加一层楼”，一百多年前，德国数学史家汉克尔就如此形象地指出了数学与其他自然科学的显著差异，形象地指出了数学这门学科的积累特性.从这个意义上说，不了解数学史就不可能全面了解数学科学.

《普通高中数学课程标准（实验）》指出“数学是人类文化的重要组成部分，不同的民族有不同的数学传统.数学课程应适当介绍数学的历史、应用和发展趋势；数学对推动社会发展的作用；数学的社会需求；社会发展对数学发展的推动作用；数学科学的思想体系；数学的美学价值；数学家的创新精神.数学课程应帮助学生了解数学在人类文明发展中的作用；逐步形成正确的数学观”.

一、数学史选修课开课的意义

数学科学作为一种文化，不仅是整个人类文化的重要组成部分，而且始终是推进人类文明的重要力量.在高中开设数学史选修课，能使学生了解到数学知识、方法、思想产生的历史背景，加深对数学概念、方法、思想的理解，把握数学的本质和发展脉络，使学生养成独立思考、积极探索的习惯，培养学生的创造性思维能力和激发学习数学的兴趣.

1.数学史的科学意义

每一门科学都有其发展的历史，数学科学具有悠久的历史，与自然科学相比，数学更是积累性科学，其概念和方法更具有延续性，比如古代文明中形成的十进位制记数法和四则运算法则，我们今天仍在使用，数学传统与数学史材料可以在现实的数学研究中获得发展.国内外许多著名的数学大师都具有深厚的数学史修养或者兼及数学史研究，并善于从历史素材中汲取养分，做到古为今用，推陈出新.

2.数学史的文化意义

美国数学史家m.克莱因曾经说过：“一个时代的总的特征在很大程度上与这个时代的数学活动密切相关.这种关系在我们这个时代尤为明显”“数学不仅是一种方法、一门艺术或一种语言，数学更主要是一门有着丰富内容的知识体系，其内容对自然科学家、社会科学家、哲学家、逻辑学家和艺术家十分有用，同时影响着政治家和神学家的学说”.数学广泛影响着人类的生活和思想，是形成现代文化的主要力量.数学史是从一个侧面反映的人类文化史，又是人类文明史的最重要的组成部分.许多历史学家通过数学这面镜子，了解古代其他主要文化的特征与价值取向，教育人们去进行抽象的推理，激发人们对理想与美的追求.

3.数学史的教育意义

歌德曾经说过：“一门科学的历史就是这门科学本身.”数学的历史也就是数学本身，或者至少也是数学本身不可分割的一部分.数学史不仅可以促进学生对数学的理解，最重要的是，它能使学生对数学的理解更加完整.将数学史适当地应用到数学教学中，发挥数学史料的教育功能，是数学教育改革的一项有力措施.

例1天才数学家欧拉介绍.

图1

欧拉是数学史上著名的数学家，他在数论、几何学、天文数学、微积分等好几个数学的分支领域中都取得了出色的成就.欧拉的一生，是为数学发展而奋斗的一生，他那杰出的智慧，顽强的毅力，孜孜不倦的奋斗精神和高尚的科学道德，永远是值得我们学习的.

通过介绍数学家的感人的历史事例，有助于了解数学的发生和发展；了解历史上中外杰出的数学家的生平和数学成就；有助于感受前辈大师严谨治学、锲而不舍的探索精神；有助于培养兴趣、开阔视野、开拓创新，更深刻体会数学对人类文明发展的作用.

4.数学史的“现实”意义

反映数学的科学和人文价值，是高中数学课程建设的基本理念.自高考实行各省市自主命题以来，开创了百花齐放、百家争鸣的良好局面，也使数学史闪耀出灿烂光芒.

作为高中数学教师，要不断更新教育理念，时刻关注教育发展和改革动向.我们不但可以通过对数学史的研究改进课堂教学，而且还要关注高考数学试题的数学史背景（命题背景、解题背景）.

例2（2014年高考湖北卷文10/理8）《算数书》竹简于上世纪八十年代在湖北省江陵县张家山出土，这是我国现存最早的有系统的数学典籍，其中记载有求“□盖”的术：“置如其周，令相乘也．又以高乘之，三十六成一．”该术相当于给出了由圆锥的底面周长L与高h，计算其体积V的近似公式它实际上是将圆锥体积公式中的圆周率π近似取为3.那么，近似公式相当于将圆锥体积公式中的π近似取为（）.

例3（2014年高考陕西卷理14）观察分析表中的数据：

?

猜想一般凸多面体中F、V、E所满足的等式是________．

上述两个例子均来源于2014年高考试题，一个出自《算数书》，一个需要考生通过推理得出多面体欧拉公式.

二、数学史选修课开课模式

高中阶段数学史主要有两种呈现方式，一是在数学教材中以各种方式渗透，这在高中的数学教材中都有体现；二是在高中阶段开设专门的选修课程.

从课程实施的目的来说，“数学史”希望使学生了解数学发展过程中若干重要事件、重要人物和重要成果，初步了解数学产生和发展的过程，体会数学对人类文明发展的作用，提高学习数学的兴趣，加深对数学的理解，感受数学家严谨的态度和锲而不舍的探索精神，进而提高学生的数学素养.

1.专题呈现

由于课时安排无法满足对数学史系统性和完整性的阐述，因此数学史选修课宜采用专题形式展开，这样更容易体现课程内容的弹性，有重点地突出思想.专题教学，就是按照问题来组织课堂教学，打破原有教材的章节体系限制，选取若干专题作为深入分析讲授的教学方式.在对教材内容全面系统把握的基础上，结合现实需要和学生特点，将教材中的知识点用专题的形式贯穿起来，重在每个专题内知识结构的系统性和严谨性以及回答学生的思想困惑问题.这种教学方式至少存在以下两大优势：第一，专题式教学具有针对性、现实性的特征，能够克服学生内在学习动力不足的问题，有效提高学生学习的兴趣；第二，专题式教学具有开放性特征，能够充分发挥教师的专业所长，有效提高教学质量和科研水平.

专题呈现，内容要反映出数学发展的不同时代的特点，要讲史实，更重要的是通过史实介绍数学的思想方法.内容的安排可以采取多种形式，既可以由古至今，追寻数学发展的历史；也可以从现实的、学生熟悉的数学问题出发，追根溯源，回眸数学发展中的重要事件和人物.

下面是笔者开设的“数学史”选修课的专题设置表.

表1：数学中选修课课程内容安排

?

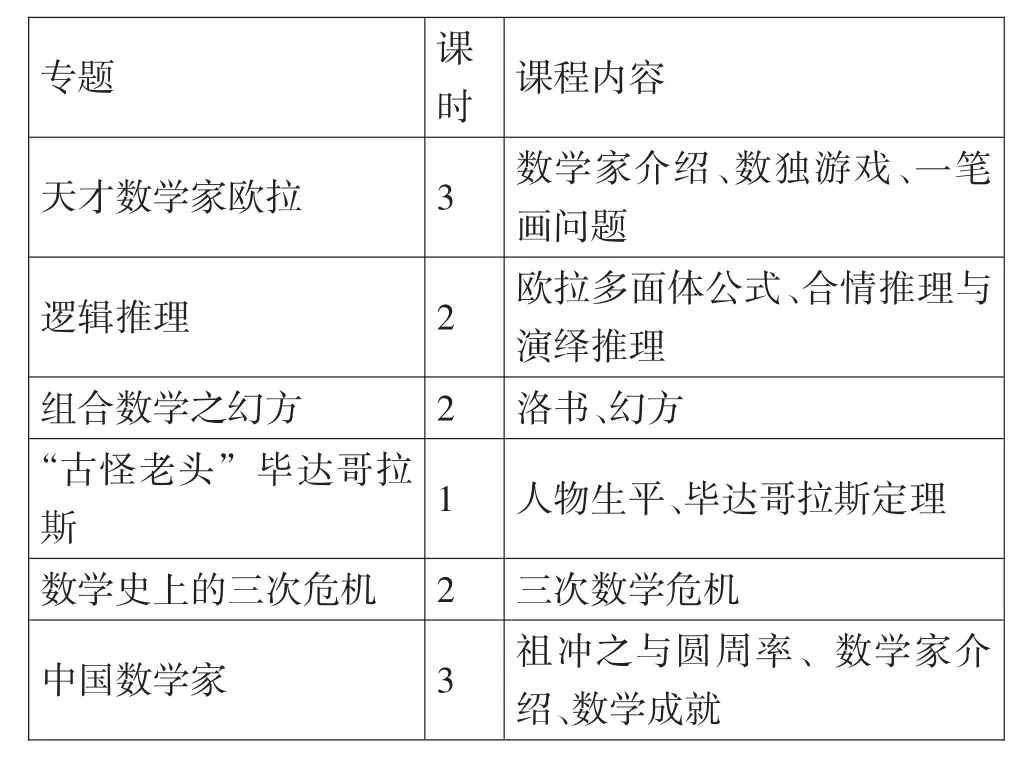
历史上一连串的数学悖论动摇了人们对数学可靠性的信仰，数学史上曾经发生了三次数学危机.数学悖论的产生和危机的出现，不单给数学带来麻烦和失望，更重要的是给数学的发展带来新的生机和希望，促进了数学的繁荣.危机产生、解决、又产生的无穷反复过程，不断推动着数学的发展，这个过程也是数学思想获得重要发展的过程.

例4专题5《数学史上的三次危机》教学过程：危机发生的背景→危机的起源→危机的解决→危机产生的影响.（以第一次数学危机为例）

（1）背景.

第一次危机发生在古希腊，当时人们对于无理数的概念一无所知.数学家毕达哥拉斯建立了带有浓厚宗教色彩的毕达哥拉斯学派.这个学派进行了大量的教学研究，并取得了众多的数学发现，他们还提出了“万物皆数”的论断，指出“万物都可以归结为整数之比”并且相信宇宙的本质就在于这种“数的和谐”.

（2）起源.

①“万物都可以归结为整数之比”.

对于任意两条线段，毕达哥拉斯学派的成员相信上面的操作过程总会在进行了有限步之后结束，他们相信，只要有耐心总能找到那个度量单位.所以任何两个同类量都是可通约的，即万物都归结为整数之比.

②希帕索斯悖论.

古希腊人错误地认为，宇宙间的一切现象都归结为整数或整数之比.希帕索斯根据勾股定理通过逻辑推理发现等腰直角三角形的直角边与斜边不可公度！即有理数并非一切数，存在有理数以外的数，有理数不可以完全填满整条线段.这就是希帕索斯悖论：存在不可公度量！

（3）危机的解决.

①无理数的出现.

毕达哥拉斯学派相信任何两条线段a与b都可公度，用我们现在的语言表述就是指任何两条线段的比是整数或是一个分数.简言之，是一个有理数.而希帕索斯不可公度量的发现就是：等腰直角三角形的直角边与斜边的比既不是一个整数，也不是一个分数，或者简言之，不是一个有理数，而是一个当时人们完全不了解的全新的数，这类数后来被称为无理数.人类历史上诞生的第一个无理数就是希帕索斯发现的

②悖论所引发的问题.

无理数的发现被认为是悖论，动摇了毕达哥拉斯学派的数学与哲学根基，它将推翻毕达哥拉斯学派“万物皆数”的基本哲学信条，摧毁了建立在“任何两条线段都是可通约的”这一观点背后的数学观念.更重要的是，这一发现摧毁了人们通过经验与直觉获得的一些常识.

（4）第一次数学危机的影响.

希帕索斯悖论的出现，导致了第一次数学危机，这一危机的影响是巨大的，它不仅推动了数学及其相关学科的发展，使古希腊数学的基础发生了根本性的变化，而且推动了整个科学的发展，第一次数学危机让人们第一次认识到了无理数的存在，无理数从此诞生了，之后，许多数学家正式研究了无理数，给出了无理数的严格定义，提出了一个含有有理数和无理数的新的数类——实数，并建立了完整的实数理论，为数学分析的发展奠定了基础.在古希腊，数学和哲学是结盟的，哲学使古希腊的数学趋于抽象和真理，正是由于古希腊的哲学背景，使其有可能建立世界上第一个数学公理系统，并最终导致了近代科学的诞生.

2.游戏呈现

游戏“题内有话、话外有话”，教师应该更多地携“数学游戏”进入课堂.皮亚杰认为“智慧自游戏发端，活动是连接主客体的桥梁”.

图2

例5故事发生在18世纪的哥尼斯堡城.流经那里的一条河中有两个小岛，还有七座桥把这两个小岛与河岸联系起来，那里风景优美，游人众多.在这美丽的地方，人们议论着一个有趣的问题：一个游人怎样才能不重复地一次走遍七座桥，最后又回到出发点呢？

直到1836年，瑞士著名的数学家欧拉才证明了这个问题的不可能性.

图3

欧拉解决这个问题的方法非常巧妙.他认为：人们关心的只是一次不重复地走遍这七座桥，而并不关心桥的长短和岛的大小，因此，岛和岸都可以看作一个点，而桥则可以看成是连接这些点的一条线.这样，一个实际问题就转化为一个几何图形（如图3）能否一笔画出的问题了.

所谓图的一笔画，指的就是：从图的一点出发，笔不离纸，遍历每条边恰好一次，即每条边都只画一次，不准重复.易知：能一笔画出的图首先必须是连通图.

欧拉定理：①凡是由偶点组成的连通图，一定可以一笔画成，画时可以任一偶点为起点，最后一定能以这个点为终点画完此图；②凡是只有两个奇点（其余均为偶点）的连通图，一定可以一笔画完，画时必须以一个奇点为起点，另一个奇点为终点；③其他情况的图，都不能一笔画出.

好的数学游戏，不仅可以充实学生的游戏生活，而且可以激发他们学习数学的兴趣，同时丰富他们的思维想象能力，在趣味盎然的气氛中发展他们的智力.正如布鲁纳所说：“游戏活动是生命的自由表现，它是生活乐趣.”

游戏与数学的相似保证了数学游戏有利于数学思想的培养，能使学生更深刻地理解数学的精神.就思想方法讲思想方法，如果直接揭示，学生会感到枯燥无味，是不能真正掌握数学思想方法的.因此数学思想必须融入内容和应用中，而把数学思想融入数学游戏中，更易为学生接受.

3.视频呈现

以学生的学为中心，以符合教学规律和学生的认知规律为前提，通过多媒体信息技术手段的使用，优化课堂设计，可以极大地发挥其优势，有利于素质教育的实施，培养学生的记忆力、思维等多项能力.恰当使用多媒体，能够培养学生主动学习的能力.

多媒体集图、文、声、像多重刺激于一体，使学生大脑的视觉、听觉等中枢都处于兴奋状态，相关知识在大脑中就会留下深刻印象.多媒体符合人类的记忆过程，多媒体展示知识空间的联系，将知识系统化，形成网络，有利于学生对知识进行比较、加工、归纳，形成理解基础上的记忆.多媒体辅助教学，有助于培养学生的分析、归纳思维能力.

图4

例6《“古怪老头”毕达哥拉斯》专题的授课采用PPT与网络视频相结合的形式，介绍了毕达哥拉斯、毕达哥拉斯学派、毕达哥拉斯定理，借助网络视频告诉学生为什么毕达哥拉斯被称为“古怪老头”.

当然在数学史教学中视频的效果也并非越多越好，教师应根据学生的认知规律和特点，恰当地选用多媒体，使多媒体成为启迪学生认知、思维的工具，而不是教学内容的展示工具.

对于“数学史”的教学，《普通高中数学课程标准（实验）》指出，“教学方式应灵活多样，可采取讲故事、讨论交流、查阅资料、撰写报告等方式进行.教师应鼓励学生对数学发展的历史轨迹、自己感兴趣的历史事件和人物，写出自己的研究报告.”教师在教学中恰当运用现代信息技术，将现代化技术与教学有机融合.

选修课教学中教学内容的选择、教学方式的优化更是需要开课教师“精打细算”，“不必追求数学发展历史的系统性和完整性，通过学生生动活泼的语言与喜闻乐见的事例呈现内容，使学生体会数学的重要思想和发展轨迹”.

三、数学史选修课的评价标准

选修课程评价过程是促进学生潜能充分发展的过程，是教师了解和研究学生、关注每一个学生在原有水平基础上主动发展的过程，是建立民主、平等、和谐的师生关系的过程，是学生正确认识自己和教师改进教学的过程.

由于选修课的性质、特点、任务、作用与必修课不完全一样，我们必须根据选修课自身的规律开展课程评价.数学史选修课是为对数学有兴趣并希望进一步提高数学素养的学生而开设的，主要是试图通过数学的历史发展线索帮助学生进一步理解数学方法和一些重要的数学思想，拓宽学生的数学视野.对于选修课的评价应该多样化，对学生评价的主要方法有观察法、调查法、测验法.

1.观察法

观察法主要指教师在课堂教学中通过观察学生行为的具体表现，对知识与能力、学习过程与方法、情感态度价值观三维目标的达成程度进行评价，特别是对学生的学习态度、学习方法以及相关的情意目标的感受程度等进行即时或历时评价，以引导学生更积极投入于学习的一种教学评价法.

教师在边教学边观察的过程中，应该重点观察学生的学习态度和学习方法，并加以正确的引导.使用观察法评价，教师对学生的行为观察不宜集中在那些行为比较突出的学生身上（反应敏捷行为活跃的学生、学习尖子、学有专长的学生、调皮的学生和学习不专心的学生等），而是要客观对待班级每一个学生行为的感受和印象，教师应明确，自己的脑海中若没有某个学生行为的印象，就应该对该学生做观察补偿或重点观察了，或者反思自己对学生的行为观察是否有所偏失.

2.测验法

测验在测评学生的课堂学习效果中扮演着极为重要的角色.测验就是通过让学生回答一系列与教育目标有关的有代表性的问题，从学生对问题的回答中提取信息，并根据一定的标准进行判断的过程.教师在编制测验题目时可根据主观性试题、客观性试题所存在的优缺点，针对检测目的进行选择.在测验编制过程中，应同时制订测验的答案和评分标准，具体包括客观性试题的标准答案、主观性试题的答案要点、评定的记分规则.

例7《数学史》选修课测试题.

（1）公式eix=cosx+isinx中e是自然对数的底，i是虚数单位，它将指数函数的定义域扩大到复数，建立了三角函数和指数函数的关系，在复变函数论里占有非常重要的地位，被誉为“数学中的天桥”.发现这个著名公式的数学家是（）.

A．高斯B.欧拉C.柯西D.牛顿

（2）历史上这个学派任意地把非物质的、抽象的数夸大为宇宙的本原，认为“万物皆数”.以“万物皆数”为信条的古希腊数学学派是（）.

A.爱奥尼亚学派B.伊利亚学派

C.诡辩学派D.毕达哥拉斯学派

（3）1955年希腊发行了一枚邮票，图案是由三个棋盘排列而成，这枚邮票是纪念两千五百年前希腊的一个学派和宗教团体──毕达哥拉斯学派，它的成立以及在文化上的贡献.邮票上的图案是对数学上一个非常重要定理的说明.它是初等几何中最精彩的，也是最著名和最有用的定理，在我国，人们称它为勾股定理或商高定理；在欧洲，人们称它为毕达哥拉斯定理.请你叙述该定理：_________________.

图5

（4）最早使用“函数”（function）这一术语，并引入函数符号y=f（x）的数学家是（），在我国，清代数学家李善兰在1859年和英国传教士伟烈亚力合译的《代微积拾级》中首次将“function”译作“函数”.

A.莱布尼茨B.约翰·伯努利

C.雅各布·伯努利D.欧拉

（5）用圆圈符号“o”表示零，可以说是（）数学的一大发明，有零号的数码和十进位制记数在公元8世纪传入阿拉伯国家，后又通过阿拉伯人传至欧洲.中国古代的筹算数码中开始没有“零”，遇到“零”就空位.数字中没有“零”，是很容易发生错误的.

A.中国B.阿拉伯C.印度D.古希腊

（6）在人类历史的早期，生活在尼罗河畔的古埃及人创造了先进的文化和高度发达的文明.古埃及文明的重要成就之一就是科学技术发明，其中数学成就引人注目.从现今遗留下来的古埃及数学文献可看出，古埃及人的数学知识包括算术、代数和几何三个方面.古埃及的数学知识常常记载在（）.

A.纸草书上B.竹片上C.木板上D.泥板上

（7）从已知的事实出发，不断运用已掌握的（知识库中的）知识推出或归纳出新的事实（包括目标结论）的过程称为推理.请问在这个逻辑思维训练中，问号处的数字是什么？

5，10，17，26，37，（？）

图6

（8）一笔画问题源于哥尼斯堡七桥问题，欧拉通过对七桥问题的研究，不仅圆满地回答了哥尼斯堡居民提出的问题，而且得到并证明了更为广泛的有关一笔画的三条结论，人们通常称之为欧拉定理.图6是一个公园的平面图，要使游人走遍每一条路不重复，请问出口和入口应设在哪儿？

（9）幻方也称纵横图，它是科学的结晶与吉祥的象征，发源于我国古代的洛书——九宫图.把“洛书”用数字表达就是一个“幻方”.下面请将1-7这七个数字填写到如图7所示的小圆圈中，使每条直径上的三个数字之和都为10.

（10）数独前身为“九宫格”，最早起源于中国.1783年，瑞士数学家莱昂哈德·欧拉发明了一种当时称作“拉丁方块”（LatinSquare）的游戏，这个游戏是一个n×n的数字方阵，每一行和每一列都是由不重复的n个数字或者字母组成的.1984年4月，在日本游戏杂志《字谜通讯Nikoil》（《パズル通信ニコリ》）上出现了“数独”游戏，提出了“独立的数字”的概念，意思就是“这个数字只能出现一次”或者“这个数字必须是惟一的”，并将这个游戏命名为“数独”（sudoku）.请完成下面的数独题.

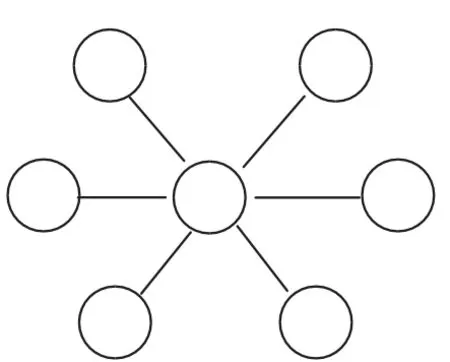
图7

图8

（11）“一个违反万物皆数的理论，葬身了一双发现的眼睛；一次对真理苦苦的追寻，造就了基础数学中最重要的课程；一回回不断地完善理论系统，奠定了数学的基石”指的是数学史上的哪三次重大事件？

（12）简述学习数学史的意义.

3.调查法

选修课程评价要重视学生个性发展、人格完善，重视积极发挥评价结果在促进学生素质全面发展中的作用.在对学生的评价中，学生应成为评价主体，重视学生在学习活动中对师生关系的实际感受，学生的学习兴趣和获得成功的体验等应成为学生评价的重要内容.

问卷调查是一种结构化的调查，其调查问题的表达形式、提问的顺序、答案的方式与方法都是固定的，而且是一种文字交流方式，因此，任何个人，无论是研究者还是调查员都不可能把主观偏见代入调查研究之中.其调查的统计结果一般都能被量化出来.

四、开设“数学史”选修课的思考

数学课程应帮助学生了解数学在人类文明发展中的作用，逐步形成正确的数学观.数学史研究的任务在于弄清数学发展过程中的基本史实，再现其本来面貌，同时透过这些历史现象对数学成就、理论体系与发展模式作出科学、合理的解释、说明与评价，进而探究数学科学发展的规律与文化本质.

在高中阶段开设“数学史”选修课的一个终极目的就是提高学生学习数学的积极性，使学生加深对数学本质的理解，增长知识面，扩大视野.应该说，“数学史”选修课的开设适应高中数学教学需求，适应数学发展现状、社会发展现状和学生心理发展现状.它的产生，会不断激起学生对数学的更大兴趣，满足学生想要深入了解数学的欲望.

当然选修课的开设具有很大的局限性，只能满足少部分学生的学习要求，同时也不能过多地结合课堂教学，对必修部分的促进作用少之又少，因此数学史的选修可以说是杯水车薪，要想更好地更全面地用好数学史，一方面教师首先要具备和不断充实数学素养和数学史知识，另一方面要在教学中恰当安排数学史的学习内容.同时对于课程的开课模式和评价标准有待于进一步的研究和实践，因此我们也相信数学史选修课的开设是一个很好的契机，借此探求数学史教学的新途径.

1.中华人民共和国教育部.普通高中数学课程标准（实验）［M］.人民教育出版社，2003.

2.张小明.HPM视角下的高中数学教学：实践与思考［J］.中学数学教学参考（上），2011（9）.

3.赵国胜.新课改背景下高中“数学史”选修课开设初探［J］.中学数学（上），2014（11）.