抗扰动的捷联惯导系统回溯参数辨识对准法
张朝飞,罗建军,侯永利
(1. 西北工业大学 航天学院,西安 710072;2. 航天飞行动力学技术重点实验室,西安 710072;3. 中国航天第十六研究所,西安 710100)
抗扰动的捷联惯导系统回溯参数辨识对准法
张朝飞1,2,罗建军1,2,侯永利3
(1. 西北工业大学 航天学院,西安 710072;2. 航天飞行动力学技术重点实验室,西安 710072;3. 中国航天第十六研究所,西安 710100)
针对捷联惯导系统参数辨识对准法航向角估计时间长且收敛速度受到计算初值影响大的问题,提出了将对准用的陀螺和加速度计采样数据存储后按时间进行正向和逆向排列,形成正向序列和逆向序列。由正向导航的解算公式推导出逆向导航的解算公式,利用公式的一致性提出了回溯误差参数辨识对准法。利用抗扰动的惯性系对准算法为回溯参数辨识法提供对准初值,应用回溯参数辨识法对误差参数反复进行逆向和正向辨识后对对准结果进行修正,能够有效提高对准精度。实验结果表明,利用相同时间的采样数据,该算法航向角的对准误差仅为改进前算法的25%。
捷联惯导系统;抗扰动;回溯;参数辨识对准
初始对准技术是捷联惯性导航系统中一项重要技术,对准的快速性和高精度是其主要的指标。目前常用的对准方法有多位置对准法和单位置对准法。其中,多位置对准算法能够提高对准参数的可观测性,但是需要增加高精度的转位机构才能实现[1-4]。单位置对准算法有:① 经典三阶调平回路及方位罗经对准法[5-6],该算法收敛缓慢,适用于舰船等长时间对准,不利于快速对准;② 卡尔曼滤波对准算法[7-8],该算法状态方程维数高,计算量大且收敛性受模型参数的影响较大;③ 参数辨识对准法[9],该算法原理简单,易于实现,因此广泛应用于捷联惯导系统的初始对准中,但该算法误差参数收敛速度慢,航向角对准时间受速度误差的影响,辨识精度差。
因此,本文在文献[9]的基础上,改进了将陀螺和加速度计的采样数据按时间顺序先进行粗对准再进行精对准的单向对准方式,提出了一种抗扰动的捷联惯导系统回溯参数辨识对准法。
通常提高对准精度的方法是减少对准时的干扰和增加对准时间,使得初始对准误差在导航误差中的所占的比重随之增加,从而易于被辨识。但对准时的干扰通常难以避免,而增加对准时间也与对准的快速性要求相矛盾。本文通过充分利用对准时间内的采样数据所包含的导航误差信息,而非单纯地增加对准时间,将对准用的采样数据存储起来,按时间顺序进行正向和逆向排序后形成正向序列和逆向序列;然后利用抗扰动的惯性系对准算法对正向序列进行粗对准,得到误差较小的粗对准结果;其次根据回溯参数辨识法对逆向序列和正向序列迭代进行对准,最终达到加快误差参数收敛速度和提高航向角对准精度的目的。
1 惯性系粗对准
载体坐标系(b系)选择前右下坐标系。导航坐标系(n系)为当地地理坐标系,本文中为东北天坐标系。惯性坐标系(ib0系)在粗对准开始时刻t0将b系在惯性空间凝固为ib0系,即。初始对准姿态矩阵为其中:

式中:L和λ分别为当地的纬度和经度,ωie为地球自转角速率,t为对准时间。C利用陀螺的输出利用等效旋转矢量法进行实时更新,因此求解 C的核心问题转换为 C的计算问题。取 t<t ≤ t <t ,其中t为012m0对准起始时刻,tm为对准结束时刻,计算得:
其中:
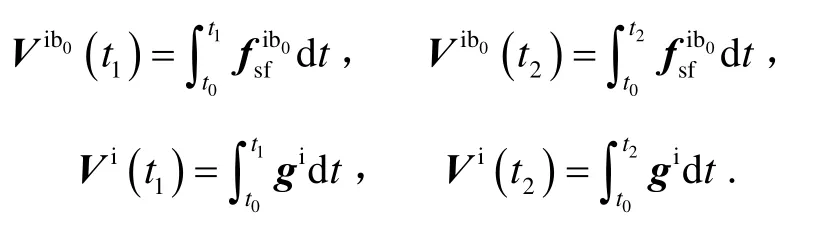
2 回溯参数辨识法精对准
2.1 正向导航算法介绍
等效旋转矢量微分方程的近似形式[10-11]为

式中:Φ为载体系从tk-1时刻到tk时刻角位置变化所对应的等效旋转矢量,ω为该时间段内的旋转角速率。
在静基座或者晃动基座对准时,忽略圆锥误差补偿项,采用单子样算法进行姿态解算,得:
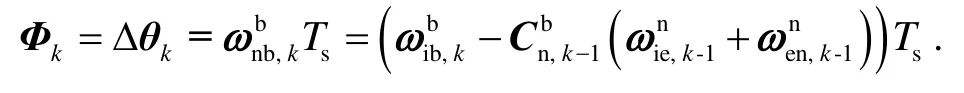
其中:
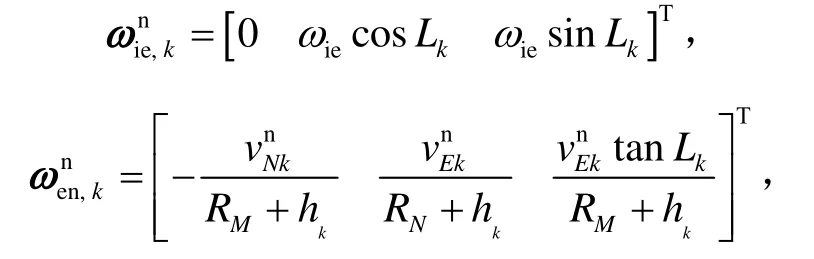
Ts= tk- tk-1为姿态更新周期。

速度微分方程为
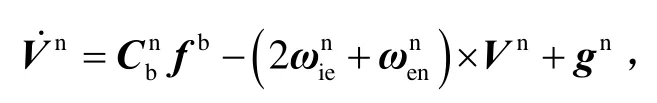
求解得:

位置微分方程为

求解得:
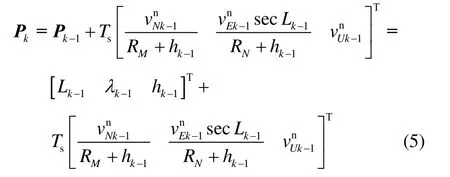
2.2 逆向导航算法推导
若正向导航长度为m,如图1所示。以m时刻的姿态、速度取反和位置作为逆向导航的初始姿态、初始速度和初始位置,将陀螺采样和地球自转角速率取反,并且对陀螺和加速度计的采样数据进行逆序处理,形成逆向数据序列。

图1 逆向导航算法原理图Fig.1 Principle of negative-direction navigation algorithm
由公式(3)可以推导出,在逆向导航过程中:


若不考虑计算误差,逆向导航时各时刻的姿态信息、位置信息与正向导航在对应时刻上的姿态信息、位置信息相同,速度信息大小相同,方向相反。
由上述推导可知,正向导航和逆向导航的解算公式相同,因此其系统误差方程也相同,逆向参数辨识法精对准的方程与正向参数辨识精对准的方程完全相同,仅对准过程中的导航信息不同。
2.3 回溯参数辨识法精对准
完成惯性系粗对准后,捷联数学平台的失准角φE、 φN、 φU均为小角度。考虑陀螺常值漂移ε和加速度计零偏▽,捷联惯导系统的失准角误差方程可以写为[9]

式中,uE、uN、uU为中间控制量:
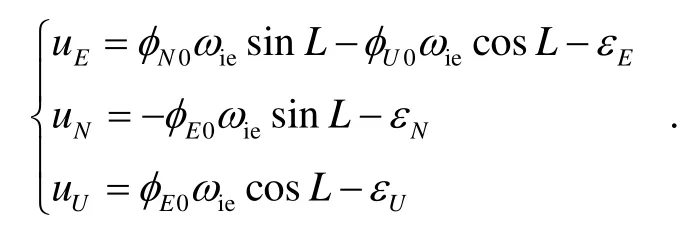
进一步,可求得水平速度误差方程为

式中,VDE、VDN分别为对做简谐波动的等效干扰加速度的积分,没有随时间增长的趋势。可将式(8)改写成:

式(11)中,Ts为采样周期, a1E=▽E- gφN0、
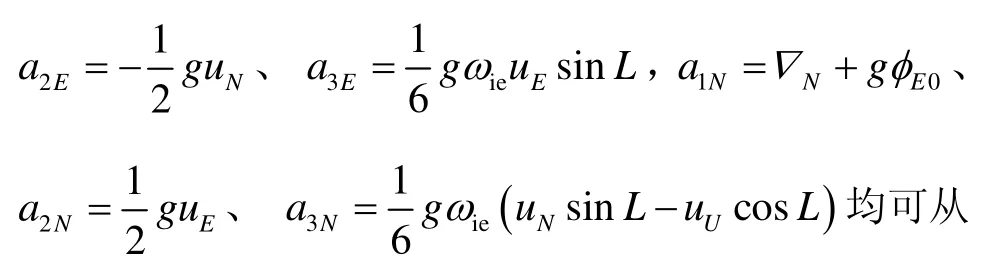
速度误差中辨识出,得:
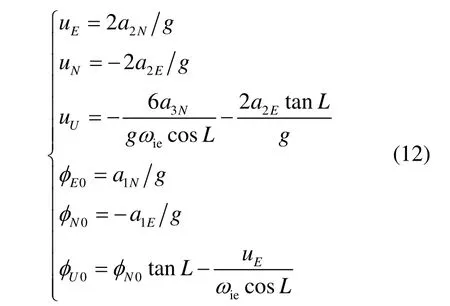
由以上分析可以得出抗扰动的回溯参数辨识对准法的具体步骤如下:
Step 1. 先保存惯组从t0到tm时刻陀螺和加速度计的输出,进行惯性系粗对准,得到逆向对准的初值C,开始进行回溯参数辨识法精对准;
Step 2. 以结束时刻tm为起始时刻,对陀螺和加速度计输出数据进行逆序处理,以惯性系粗对准得到的姿态矩阵 C作为姿态矩阵的初值,根据逆向参数辨识法进行精对准,得到精对准后的姿态矩阵;
Step 4. 执行Step 2和Step 3,即完成一次回溯参数辨识法精对准,可以反复进行多次,直到姿态矩阵解算得到的航向角逐渐收敛。
整个过程如图2所示。

图2 抗扰动回溯参数辨识对准法步骤Fig.2 Alignment approach of anti-interference backtracking parameter identification
3 实验验证
实验选用航天十六所生产的某型激光捷联惯组,激光陀螺仪等效漂移(3σ)为 0.003 (º)/h,加速度计等效零偏(3σ)为5×10-5g0,惯组固定于实验车上,在不同的时间进行6次实验。实验车静止于平坦路面上,发动机处于启动状态,上电30 min后进行数据采集,期间人为进行开关车门及上下车的动作,采集 300 s数据后停止施加干扰并关闭发动机,再静态采集300 s数据。实验结束后用G2000型陀螺经纬仪对激光捷联惯组的航向角进行测量,作为航向角的真值。
分别采用抗扰动的回溯参数辨识法和文献[9]中的参数辨识法对采样数据进行对准,表1为利用不同方法进行对准的实验结果,其中抗扰动回溯参数辨识法为对采样数据进行一次回溯参数辨识精对准的结果。
由表1中可以看出,利用300 s的采样数据进行对准,抗干扰回溯参数辨识法的对准误差为参数辨识法误差的25%,亦小于参数辨识法600 s的对准误差。图3~图5为利抗扰动的回溯参数辨识法和用参数辨识法进行对准时的对准误差,由图中可以看出,抗扰动的回溯参数辨识法的对准误差明显小于参数辨识法。
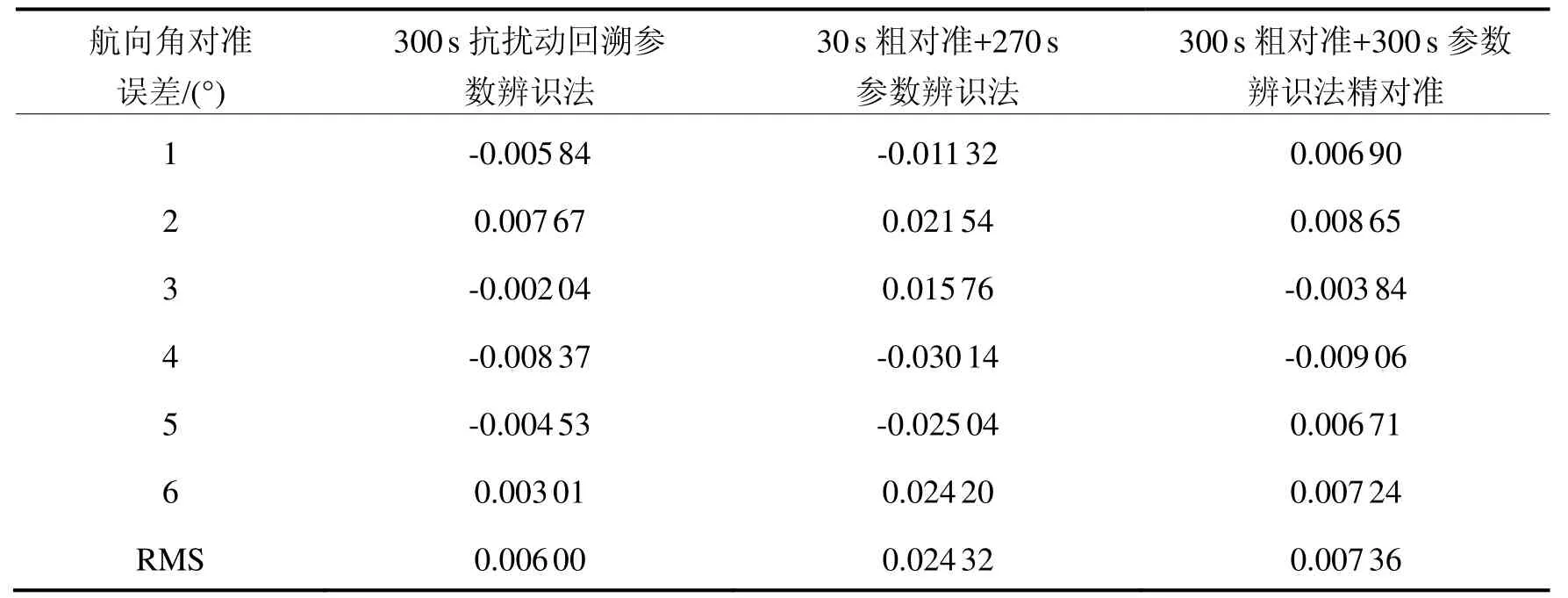
表1 三种对准方法的航向角对准误差Tab.1 Azimuth alignment errors of three alignment algorithms

图3 俯仰角误差对比Fig.3 Comparison on pitch errors
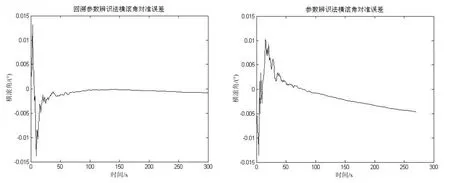
图4 横滚角误差对比Fig.4 Comparison on roll errors
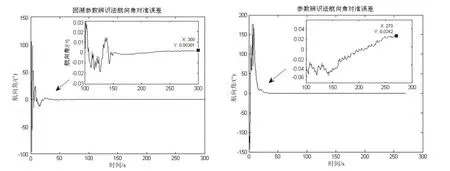
图5 航向角误差对比Fig.5 Comparison on azimuth errors
4 结 论
惯性系的粗对准能够有效地隔离外界扰动对捷联惯导系统初始对准的影响。因此,在有扰动的环境下,利用惯性系粗对准能够为回溯参数辨识精对准提供较好的初始对准值。另外,粗对准的精度与对准时间有很大关系,在一定程度上,对准的时间越长,粗对准的精度越高。抗扰动的回溯参数辨识法将对准用的采样数据按时间进行正向和逆向处理,可以将整个正向的时间序列用于粗对准,单向的参数辨识对准法仅能提供较短时间的采样数据用于粗对准,因此,相对于单向的参数辨识对准法而言,回溯参数辨识法可以有效地提高粗对准的精度。
回溯参数辨识法的本质是提高对准用的采样数据的利用率,反复对采样数据进行逆向和正向导航,然后利用导航过程中产生的速度误差去估计对准失准角。理论分析可得,经过多次的回溯,初始对准可以达到极限精度。但是,根据实验验证,初始对准的精度并不总随着回溯次数增加而提高,当回溯超过一定次数后,导航解算的速度误差不再减小,而对准精度也就不再提高。因此,在实际的应用过程中,可以根据捷联惯导系统的性能进行有限次的回溯,以达到对准精度和计算复杂度的平衡。
本文中的方法不仅适用于静基座对准,对于动基座或行进间对准,也有一定的参考价值,可以将引入的外界参考信息作为导航解算的真值,从导航误差中辨识出初始对准的误差。
(References):
[1] 付强文, 秦永元, 张金红, 等. 捷联惯导系统快速最小二乘精对准方法[J]. 中国惯性技术学报, 2012, 20(3): 278-282. Fu Qiang-wen, Qin Yong-yuan, Zhang Jin-hong, et al. Rapid recursive least-square fine alignment method for SINS[J]. Journal of Chinese Inertial Technology, 2012, 20(3): 278-282.
[2] Ma T, Gao Y. Application and comparison of two methods for alignment of FOG SINS[C]//2010 8th World Congress on Intelligent Control and Automation. IEEE, 2010: 3581-3584.
[3] Shang S T, Gao W S. Application of adaptive Kalman filter technique in initial alignment of single-axial rotation strap-down inertial navigation system[C]//Advanced Materials Research. 2012: 617-621.
[4] 刘永红, 刘明雍, 谢波. 捷联惯导系统双位置快速抗干扰对准方法[J]. 中国惯性技术学报, 2014, 22(3): 296-300. Liu Yong-hong, Liu Ming-yong, Xie Bo. Rapid antiinterference method of two-position alignment of strapdown inertial navigation system[J]. Journal of Chinese Inertial Technology, 2014, 22(3): 296-300.
[5] Silson P M G. Coarse alignment of a ship's strapdown inertial attitude reference system using velocity loci[J]. IEEE Transactions on Instrumentation and Measurement, 2011, 60(6): 1930-1941.
[6] 严恭敏. 捷联惯导系统动基座初始对准及其它相关问题研究[D]. 西安: 西北工业大学, 2008. Yan Gong-min. On SINS in-movement initial alignment and some other problems[D]. Xi’an: Northwestern Polytechnical University, 2008.
[7] Song L, Zhang C, Lu J. Self-alignment of full skewed RSINS: observability analysis and full-observable Kalman filter[J]. Journal of Systems Engineering and Electronics, 2014, 25(1): 104-114.
[8] Ma L H, Wang K L, Li H. Gyrocompass alignment method of sins based on Kalman filtering pretreatment and dynamic gain adjustment on a rocking base[J]. Information Technology Journal, 2013, 12(4): 777-783.
[9] 秦永元. 惯性导航[M]. 第二版. 北京: 科学出版社, 2014: 325-328.
[10] Savage P G. Explicit frequency-shaped coning algorithms for pseudoconing environments[J]. Journal of Guidance, Control, and Dynamics, 2011, 34(3): 774-782.
[11] Savage P G. Coning algorithm design by explicit frequency shaping[J]. Journal of Guidance, Control, and Dynamics, 2010, 33(4): 1123-1132.
Anti-interference backtracking parameter identification alignment approach for strapdown inertial navigation system
ZHANG Zhao-fei1,2, LUO Jian-jun1,2, HOU Yong-li3
(1. School of Astronautics, Northwestern Polytechnical University, Xi’an 710072, China; 2. Science and Technology on Aerospace Flight Dynamics Laboratory, Xi’an 710072, China; 3. The 16th Institute, China Aerospace Science and Technology Corporation, Xi’an 710100, China)
Since the parameter identification alignment approach of strapdown inertial navigation system has such problems as the convergent time is long and the azimuth error is affected by the initial value of recursive calculation, an identification alignment algorithm for backtracking parameters is proposed by the consistency of the formulae, in which the positive and negative direction sequences are obtained by storing and processing the alignment data of gyros and accelerometers. Based on the anti-interference coarse alignment in inertial reference frame, the negative and positive direction identification alignment is used repeatedly in the fine alignment algorithm of backtracking parameter identification alignment. Experiment results confirm that, by the new alignment algorithm, the azimuth error can be reduced by 75% without increasing alignment time.
strapdown inertial navigation system; anti-interference; backtracking; parameter identification alignment
V249.3
:A
2015-07-10;
:2015-11-11
国家自然科学基金(61004124)
张朝飞(1987—),男,博士研究生,从事捷联惯导研究。E-mail: fly060fly@qq.com
联 系 人:罗建军(1965—),男,教授,博士生导师。E-mail: jjluo@nwpu.edu.cn
1005-6734(2015)06-0733-06
10.13695/j.cnki.12-1222/o3.2015.06.007

