利用伪观测取代精密转台的原地旋转调制寻北

牛小骥，王 强，李 由,2，唐 健

（1. 武汉大学 卫星导航定位技术研究中心，武汉 430079；2. 卡尔加里大学，加拿大 卡尔加里 T2N1N4）

利用伪观测取代精密转台的原地旋转调制寻北

牛小骥1，王 强1，李 由1,2，唐 健1

（1. 武汉大学 卫星导航定位技术研究中心，武汉 430079；2. 卡尔加里大学，加拿大 卡尔加里 T2N1N4）

针对传统的多位置（如四位置）及旋转调制寻北法所需精密转位机构（如转台）带来的体积、重量、功耗和成本问题，提出了一种不依赖于精密机械旋转装置的原地寻北方法。借助基于惯性的组合导航算法，并利用惯性测量单元原地旋转（手动或自动）时位置和速度变化范围有限这一假设作为伪观测，实现与四位置法精度和效率相当的寻北。因为对伪观测的使用不需精确已知每一时刻IMU相对于底座的角度，故可从本质上消除对精密角度或角速度测量装置的依赖。大量（近100组）实测实验表明，在采用0.5 (°)/h的光纤惯导时可在4 min内达到优于1°(1 sigma)的寻北精度。因此，可在寻北精度和时间相当的条件下，大大降低传统寻北方法对系统的硬件要求，降低寻北成本。

寻北；卡尔曼滤波；旋转调制技术；伪观测信息；组合导航

陀螺寻北仪可以自主、快速、全天候地提供初始方位基准,在军事和民用工程中显示出日益广阔的应用前景[1]。陀螺寻北仪的两种经典寻北方法是四位置法和旋转调制法[2]。四位置法是基于最小二乘的思路，通过对称位置的测量不但能消除常值漂移的的影响，还能较好地降低标度因数对寻北结果的影响。但是，该方法需要精密的转位机构控制惯性测量单元（IMU）在寻北时段内分别停在不同的精确已知的角位置上，因此造成系统的体积、重量、功耗和成本的增加[3]。相对于四位置法，旋转调制寻北法凭借其对陀螺零偏的调制解调，理论上可以显著缩短寻北时间，提高寻北精度。但是，旋转调制寻北法的连续旋转方案对系统硬件结构和性能，尤其是对转台的旋转精度、转速和转动稳定性有很高的要求，即寻北精度很大程度上取决于转台精度[4-8]。为此，本文提出一种不依赖于精密机械旋转装置的原地旋转调制寻北方法，利用惯导中的陀螺器件经过在线误差补偿后的输出来推算旋转调制过程中的精密转角，然后使用基于伪观测信息[9]的组合导航算法，实现与四位置法精度和效率相当的寻北方法，显著降低了系统的体积、重量、功耗和成本。

1 基于伪观测的旋转调制寻北方案

1.1 算法概述

为了降低寻北对转台精度的依赖，本文使用IMU原地旋转（手动或使用机器）时其位置和线速度变化范围有限这两种假设分别作为伪位置观测和伪速度观测，并使用伪观测/INS组合导航卡尔曼滤波算法实现对航向角的估计。惯导的原地旋转在组合导航算法中很大程度上抵消了陀螺零偏对航向估计的影响，从而提高了航向角的估计精度[10-13]。更重要的是，因为对伪观测信息的使用不需要精确知道每一时刻的 IMU相对于底座的角度，本算法可从根本上消除对精密角度或角速度测量装置的依赖。图1给出了原地寻北算法的结构示意图。

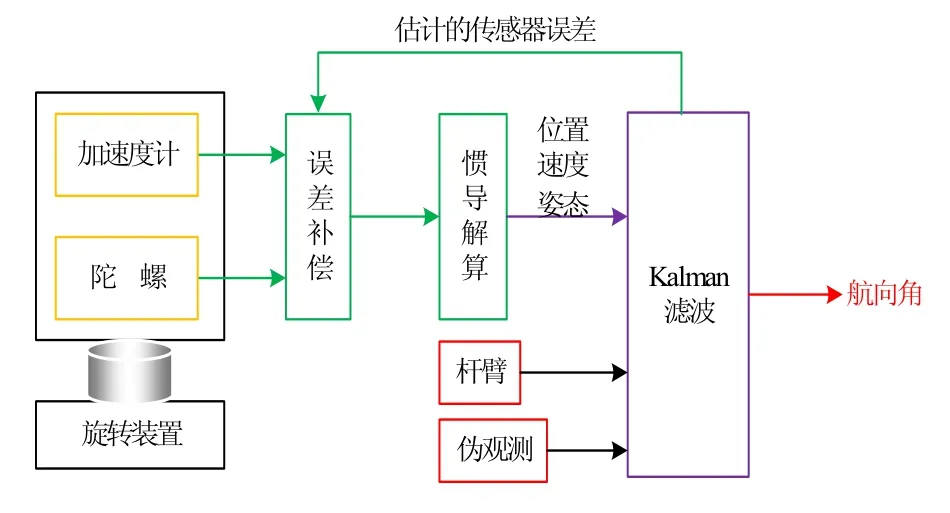
图1 原地寻北算法结构示意图Fig.1 Schematic of the in-situ north-seeking algorithm

如图1所示，本文寻北算法主要包括几个方面：惯导解算、IMU误差建模、伪观测/INS组合导航卡尔曼滤波，以及杆臂的处理。伪观测的引入和其与 INS的组合导航卡尔曼滤波是本文的重点，也是取代精密转位装置为INS提供修正的关键。此外，本研究发现，杆臂的存在将影响寻北性能，并因此提出了存在杆臂情况下的伪观测/INS组合方案。本节接下来将对寻北算法的各主要模块分别进行描述。

1.2 惯导解算

惯导解算主要思想：使用IMU量测的角速度和比力（或角增量和速度增量），结合IMU初始导航状态（位置、速度和姿态），不断预测IMU导航状态。具体来讲，首先使用陀螺测量的角速度向量进行姿态更新；然后，利用姿态信息将加速度计测量的比力向量从IMU坐标系（XYZ坐标系）转换到导航坐标系（北东地坐标系）；之后，在导航坐标系内将重力向量加入比力构成加速度向量；之后，对加速度进行积分并结合上一时刻速度求得当前时刻的速度；在对速度进行积分并结合上一时刻位置求得当前时刻的位置。具体的惯导算法可参考文献[14]。图2为惯导算法示意图，图中 rn和 vn分别为IMU位置和速度，为IMU坐标系到导航坐标系的姿态转换矩阵，为地球坐标系到导航坐标系的方向余弦矩阵， fb和 ω分别为比力和角速度向量在 IMU坐标系内的投影，ω和 ω分别为地球自转角速度和由于 IMU在地球曲面运动造成的角速度，gn为本地重力向量， 符号 “×”表示两个向量的叉乘， 符号“ω” 表示 “β”坐标系相对于“α” 坐标系的角速度在“χ”坐标系内的投影；“b”、“n”、“e”和 “i”依次代表IMU坐标系、导航坐标系、地球坐标系和惯性坐标系。

图2 惯导算法示意图Fig.2 Schematic of the inertial navigation algorithm

1.3 IMU误差建模

仅考虑传感器零偏、标度因数和噪声的情况下，加速度计和陀螺输出误差模型为

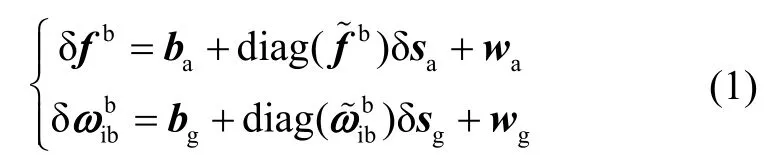
式中：δ fb和 δω分别为比力和角速度误差，ba和bg依次为加速度计和陀螺的零偏，δsa和δsg分别为加速度计和陀螺的标度因数误差，符号“diag(·)”表示一个向量构成的对角阵，wa和wg分别为加速度计和陀螺测量噪声。

1.4 伪观测/INS卡尔曼滤波状态方程

本文在导航坐标系下对惯性导航微分方程进行建模[15]：

式中：δrn、δvn和ψ分别为位置(纬度、经度、高程)误差、速度误差以及姿态角旋转矢量误差在n系中的投影；δgn是重力误差在n系中的投影；δr˙n、δv˙n、ψ˙依次为各量的时间微分；fn为n系中比力向量。

零偏和标度因数误差均建模为一阶高斯马尔科夫过程：

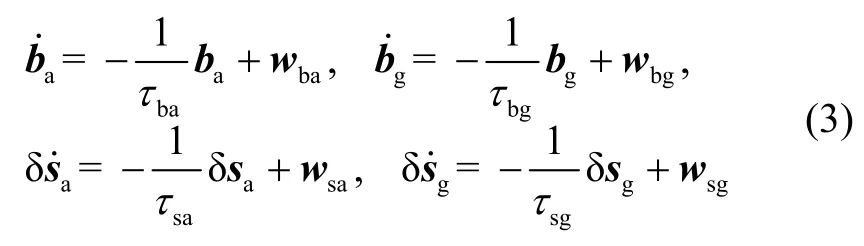
式中：τba、τbg、τsa及τsg分别代表各传感器误差的相关时间，wba、wbg、wsa及wsg为驱动白噪声[16]。

使用上述惯性导航微分方程，卡尔曼滤波连续时间状态方程可建模为

式中：x(t)为状态参数阵，F(t)为系统状态的转移矩阵，w(t)为系统状态的白噪声过程，G(t)为系统状态噪声的驱动阵。其中状态量为21维：

离散状态方程为

式中：xk、xk-1分别为k和k-1时刻的状态向量，Φk,k-1为离散后的状态转移矩阵，Γk-1为系统噪声驱动阵，Wk-1为状态的噪声向量。忽略Φk,k-1中关于Δt=tk-tk-1的二次项，Φk,k-1可表示为如下形式：

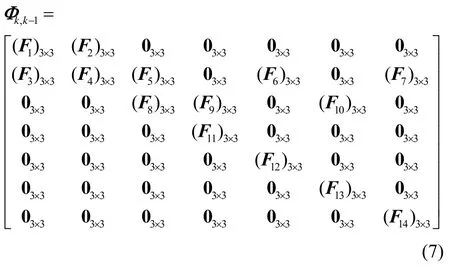
式中：

其中，I为单位阵，0i×j为i×j的零矩阵，i＞0, j＞0。

1.5 伪观测/INS卡尔曼滤波观测方程

本文利用 IMU原地旋转条件下的伪位置和伪速度约束代替GNSS位置和速度信息以完成寻北。具体的伪位置和伪速度模型为

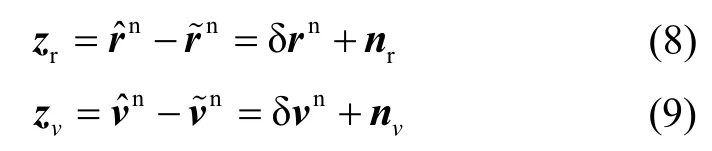
式中：zr和zv分别为位置和速度量测向量，rˆn和vˆn为INS预测的位置和速度向量，n和n分别为伪位置和伪速度向量，n为常值，n=0，nr和nv分别为位置和速度量测噪声。实际操作中IMU的位置和线速度变化在卡尔曼滤波量测噪声阵（R）中体现。

1.6 包含杆臂的伪观测/INS卡尔曼滤波观测方程

由于伪观测是基于 IMU旋转过程中位置和线速度变化范围有限这一假设，因此针对实际使用过程中IMU的位置和速度有可能变化这一现象，本文也给出了相应的解决方案。杆臂包含两部分：系统性部分和随机性部分。系统性部分为常值，如将IMU安装在转台上进行寻北时，杆臂为IMU测量中心到转台面旋转中心的距离；随机性部分多不为常值，如在不使用转台的情况下（如手动旋转IMU），杆臂为IMU测量中心至IMU在惯性坐标系中的旋转中心的距离。本文推导了包含系统性杆臂误差的伪观测量测方程，并将随机性杆臂误差在卡尔曼滤波量测噪声阵(R)中体现。

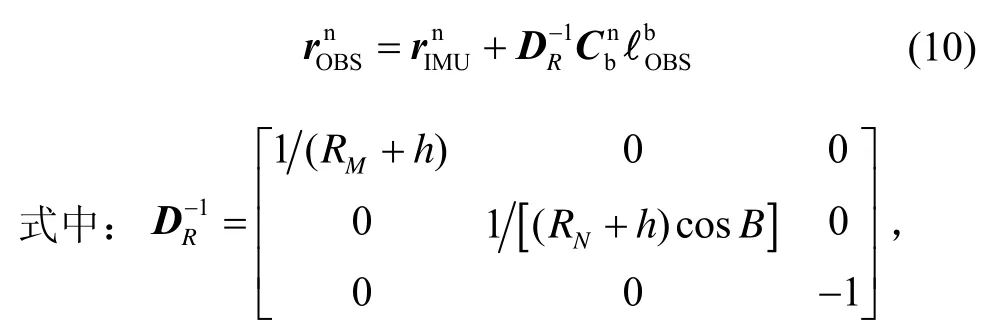
RM和RN为子午圈半径和卯酉圈半径，B表示纬度，h表示高程。对式(10)求导可得：

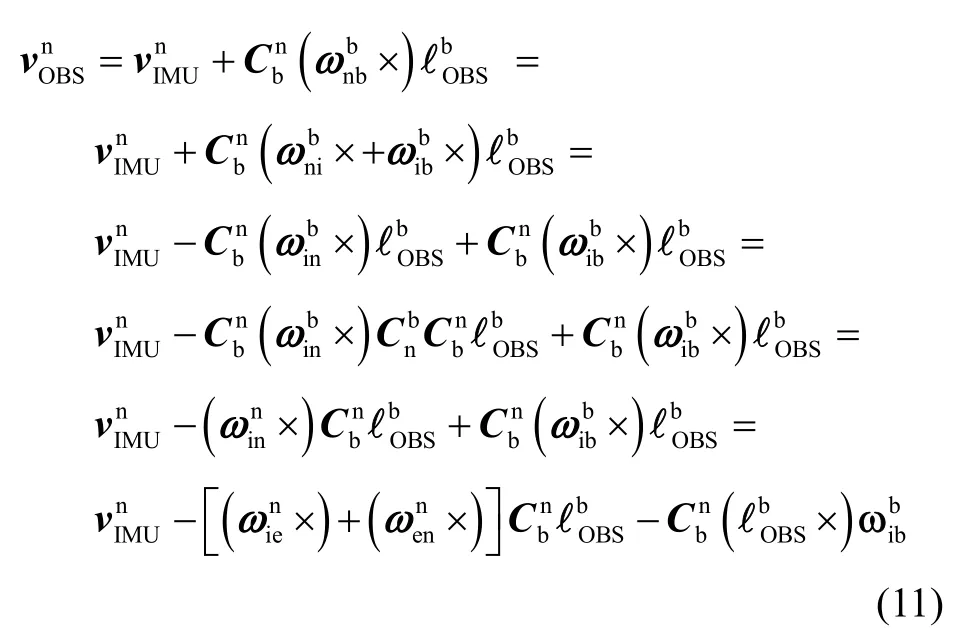
利用式(10)，得伪位置估计为

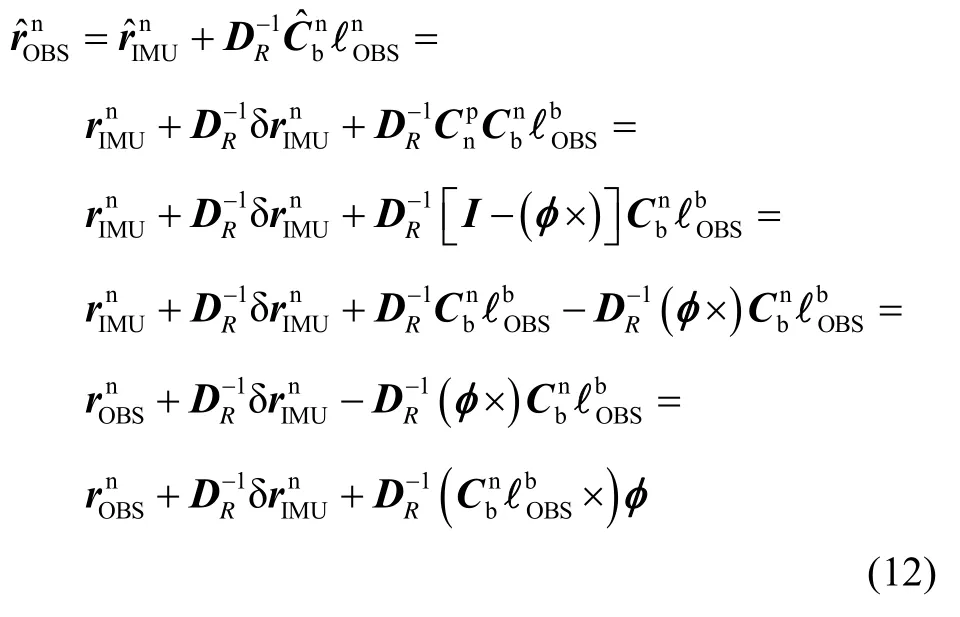
伪位置观测量可以建模为

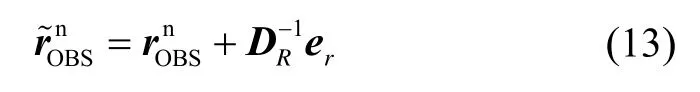
式中：er表示位置误差。则由(12)(13)可得如下松组合位置观测模型：

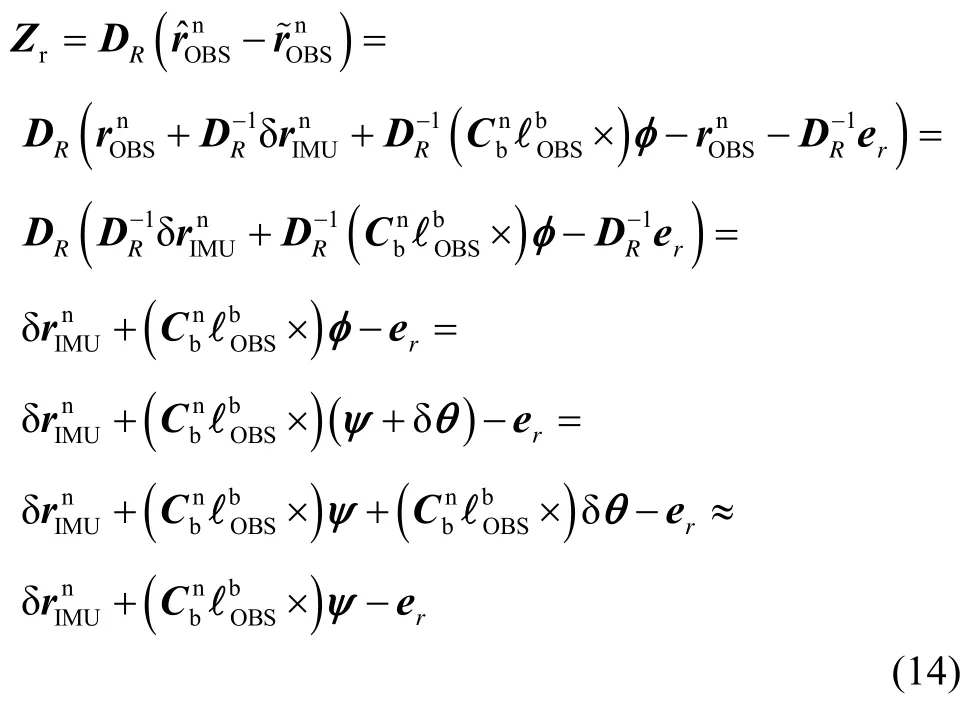
对式(17)做扰动分析，得到伪速度估计：

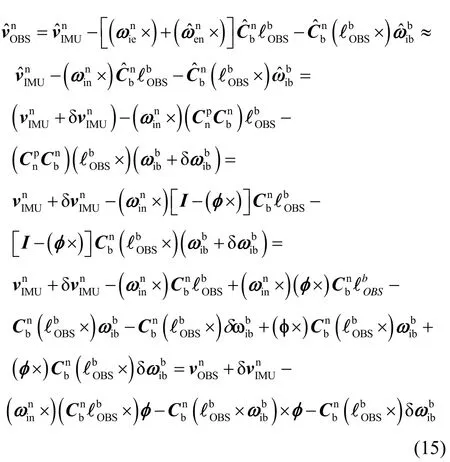
又伪速度测量可以写成：

故根据式(15)(16)，松组合KF速度观测模型为

“伪位置+伪速度”观测模型为

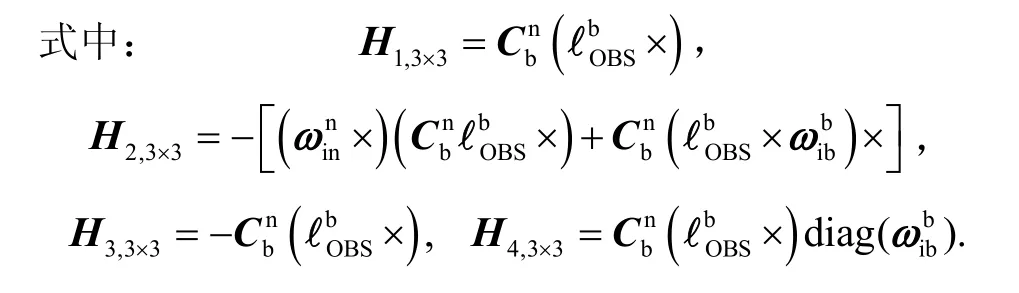
1.7 卡尔曼滤波器参数设置

卡尔曼滤波主要参数包括初始状态协方差矩阵P0、状态噪声阵Q和量测噪声阵R。初始协方差阵P0为对角阵，其值在程序的配置文件中设置，分别对应初始位置、速度和姿态标准差信息、陀螺零偏标准差、加速度计零偏标准差、陀螺标度因数标准差、加速度计标度因数标准差信息。

系统噪声方差阵Q为对角阵，其值根据传感器的角度随机游走、速度随机游走、零偏标准差、标度因数标准差信息计算。

量测噪声方差阵R的值根据实际情况下IMU测量中心可能的位置和速度变化进行设置。若采用机械装置控制旋转，则量测噪声较小；若采用如手动旋转等方式，则量测噪声较大。

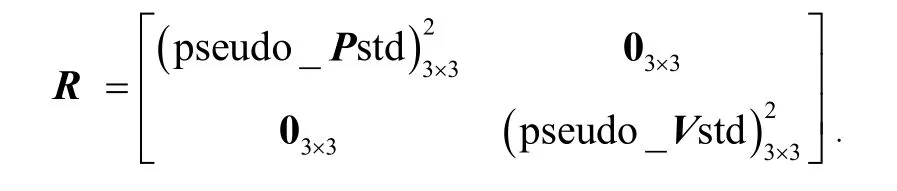
1.8 卡尔曼滤波预测与更新

预测：

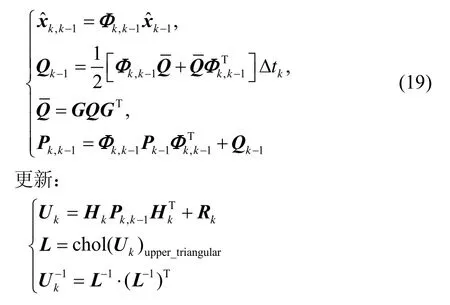
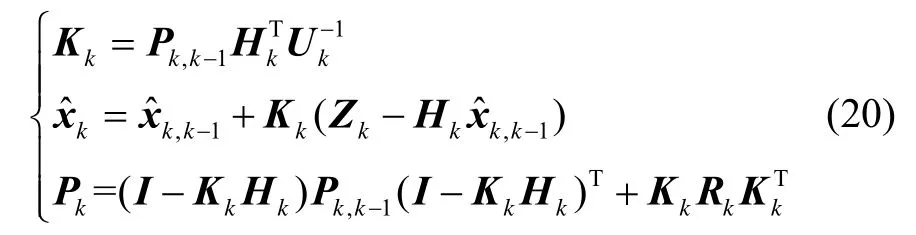
根据上述状态方程和量测方程，通过卡尔曼滤波算法，可估算出航向角，即寻北角度。

2 实验和分析

为了论证本方法寻北的精度，本文使用转台控制IMU旋转，并计算四位置寻北结果作为对比参考，而在寻北计算中不使用任何转台提供的角位置或角速度信息。实测实验在武汉大学转台实验室进行，实验室坐标为纬度φ=30.51667°，经度λ=114.3556°。使用的光纤捷联惯导器件指标如下：陀螺零偏稳定性为0.5 (°)/h，角度随机游走为0.05 (°)/√h；三轴加速度计零偏稳定性为 100 μg，速度随机游走为 0.1 ms/√t。

依据文献[17]中陀螺角度随机游走(ARW)对惯导系统初始对准影响的相关公式，可计算出在实验室位置4 min内ARW对寻北的影响为 0.8563°，陀螺ARW和零偏对三轴单位置寻北精度总的影响为2.3709°。

下面将对四位置法和本文的原地寻北法的实测进行分析：

四位置法寻北基于最小二乘思路，其精度主要受陀螺ARW的影响；原地寻北基于卡尔曼滤波的思路，水平面内常值漂移在旋转过程中被调制，通过积分解调消除，寻北精度也主要受ARW的影响。因此该原地寻北方法在理论上有望达到与四位置法相当的寻北精度。

本次实验四位置寻北法计算航向角采用的是多位置寻北的最小二乘原理[1]。通过统计96个样本的寻北结果，得到其均方根（RMS）为 0.8604°。接下来将会对原地寻北法的实测进行分析。

原地寻北实验数据采集过程描述：先在初始角位置静态20 s，然后进行总时长达3 min 20 s的连续正反交替旋转（交替时长是灵活选择的），最后转回到初始位置静态20 s，寻北总时长4 min。

杆臂效应是影响寻北精度的重要因素，也是工程应用中无法回避的问题。杆臂设置不正确会造成杆臂效应，杆臂效应增大会造成位置误差增大，如此伪观测/INS组合导航算法不能对陀螺零偏、航向角等参数进行很好的估计。图3为不同杆臂条件下，陀螺零偏的估计曲线，该图表明对于高精度寻北必须考虑杆臂的影响。正因为如此，本研究提出了包含杆臂信息的伪观测/INS卡尔曼滤波量测方程。

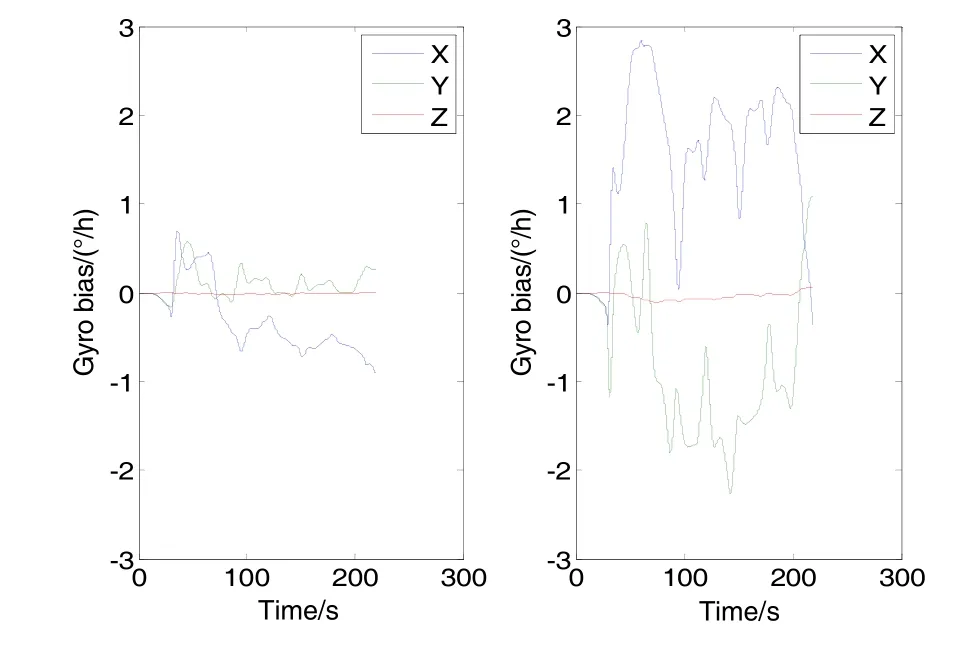
图3 不同杆臂下原地寻北陀螺零偏估计曲线（左图：正确杆臂 右图：错误杆臂）Fig.3 Estimation of gyro bias by the in-situ north-seeking method with different lever arms (Left: correct lever arm Right: wrong lever arm)

图4为一次实验初始航向角给定 -10°（初始航向角真值为0°）时的航向角误差收敛曲线图。寻北1 min后，解算结果趋于稳定，该图说明了本文所提出的原地寻北方法的可行性。

图4 单次实验原地寻北航向角误差输出曲线Fig.4 An example of heading error convergence plot by the in-situ north-seeking

图5为多个样本原地寻北航向角误差输出曲线，呈现了方位角解算过程中误差的变化趋势，可见寻北时间大于2 min后，所有样本结果趋于稳定。该图也说明了原地寻北的结果与初始角位置的选取无关。

图5 原地寻北航向角误差输出曲线Fig.5 Heading error convergence plots by the in-situ north-seeking

图6为原地寻北每次实验结果航向角误差分布图。96个样本解算结果中，除了一个粗差，其余 95样本的解算结果均在白噪声影响的3倍中误差内。仔细观察图6结果会发现：寻北结果偏差普遍偏负，这应该是初始航向角统一设定为比真值小 10°（即初始航向误差为-10°）引起的；多次寻北结果之间没有相关性，与白噪声对寻北结果的影响特征相符。

根据上述96个样本，统计出的RMS为0.8633°。统计结果表明该原地寻北方法能达到优于 0.9°(4 min)的寻北精度。

图6 原地寻北每次实验结果航向角误差分布图Fig.6 Heading errors of the in-situ north-seeking in multiple experiments

3 结 论

本文借助组合导航算法和载体原地旋转条件下的伪位置和伪速度观测，提出了一种不依赖于精密机械旋转装置的原地旋转调制寻北方法。此外，本文发现了杆臂，即IMU测量中心到伪观测中心（IMU相对惯性坐标系的旋转中心）的向量对寻北精度的影响，并推导了包含杆臂的伪观测/INS量测方程。

通过近 100次实验结果验证了其正确性和可行性。实验结果统计表明，中低等级光纤惯导（0.5 (°)/h的零偏稳定性）在 4 min内的寻北精度能够达到0.8633°(RMS)，其精度和效率与四位置法（0.8604° (RMS)）相当。杆臂对比实验表明，该原地旋转调制寻北方法需要考虑伪观测的杆臂的影响。

由于不需要精密转台，而只需要一定程度的旋转运动，该方法与传统多位置法和旋转调制法对比，具有独特的体积、重量、功耗和成本优势。该方法特别适用于载体本身就有连续旋转运动的应用场景，例如做连续方位扫描的雷达、旋转火箭弹等。

（References）：

[1] 段苛苛. 基于光纤陀螺的寻北系统关键技术研究[D].北京交通大学博士学位论文, 2014-07. Du ke-ke. Study on the key technology of north seeking system based on fiber optic gyroscope[D]. Beijing: Beijing Jiaotong University, 2014-07.

[2] 王海明, 李四海. 一种纬度未知的全姿态光纤陀螺寻北方法[J]. 中国惯性技术学报, 2014, 22(1): 63-66. Wang Hai-ming, Li Si-hai. Seeking north method for fiber optic gyroscope north-seeker at all-attitude and unknown latitude[J]. Journal of Chinese Inertial Technology, 2014, 22(1): 63-66.

[3] Duan K K, Li D H, Pei R Z. Study on the error of fourposition north seeking system based on the single axis fiber optic gyroscope[J]. Advanced Materials Research, 2012, 503: 1158-1163.

[4] Ben Y, Chai Y, Gao W, et al. Analysis of error for a rotating strap-down inertial navigation system with fibro gyro[J]. Journal of Marine Science and Application, 2010, 9(4): 419-424.

[5] Lv P, Liu J, Lai J, et al. Decrease in accuracy of a rotational SINS caused by its rotary table’s errors[J]. Int. J. Adv. Robot. Syst, 2014, 11: 1-10.

[6] Sun W, Xu A G, Che L N, et al. Accuracy improvement of SINS based on IMU rotational motion[J]. Aerospace and Electronic Systems Magazine, 2012, 27(8): 4-10.

[7] Gao W, Zhang Y, Wang J. Research on initial alignment and self-calibration of rotary strapdown inertial navigation systems[J]. Sensors, 2015, 15(2): 3154-3171.

[8] Yuan B, Liao D, Han S. Error compensation of an optical gyro INS by multi-axis rotation[J]. Measurement Science and Technology, 2012, 23(2): 025102.

[9] Li Y, Niu X, Zhang Q, et al. An in situ hand calibration method using a pseudo-observation scheme for low-end inertial measurement units[J]. Measurement Science and Technology, 2012, 23(10): 105104.

[10] Hong S, Lee M H, Chun H H, et al. Observability of error states in GPS/INS integration[J]. IEEE Transactions on Vehicular Technology, 2005, 54(2): 731-743.

[11] Li Y, Chen Q, Niu X, et al. Simulation analysis for the influences of vehicle maneuvers to the attitude estimations of GNSS/INS navigation systems[C]//China Satellite Navigation Conference 2012 Proceedings. Springer Berlin Heidelberg, 2012: 679-694.

[12] Li Y, Li Y, Rizos C, et al. Observability analysis of SINS/GPS during in-motion alignment using singular value decomposition[C]//Advanced Materials Research. 2012, 433: 5918-5923.

[13] Wu Y, Zhang H, Wu M, et al. Observability of strapdown INS alignment: A global perspective[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(1): 78-102.

[14] Noureldin A, Karamat T B, Georgy J. Fundamentals of INS, GPS and their integration[M]. Springer Science & Business Media, 2012: 1-312.

[15] Shin E H. Estimation techniques for low-cost inertial navigation[J]. UCGE report, 2005, 20219.

[16] Niu X, Zhang Q, Gong L, et al. Development and evaluation of GNSS/INS data processing software for position and orientation systems[J]. Survey Review, 2015, 47(341): 87-98.

[17] 朱奎宝, 张春熹, 宋凝芳. 光纤陀螺角度随机游走对惯导系统影响[J]. 压电与声光, 2007, 29(3): 292-294. Zhu Kui-bao, Zhang Chun-xi, Song Ning-fang. Effection of angle random walk of fiber optic gyro(FOG) on INS[J]. Piezoelectrics & Acoustooptics, 2007, 29(3): 292-294.

North-seeking based on in-situ rotation-modulation using pseudo-observation scheme without precise turntable

NIU Xiao-ji1, WANG Qiang1, LI You1,2, TANG Jian1
(1. GNSS Center, Wuhan University, Wuhan 430079, China; 2. University of Calgary, Calgary T2N1N4, Canada)

Traditional multi-position (e.g., four-position) and rotation-modulation based north-seeking methods require a sophisticated indexing mechanism (e.g., a precise turntable), which results in high volume, weight, power consumption and costs. In this paper, an in-situ north-seeking method based on rotation-modulation is put forward, which does not rely on any precise mechanical rotation device. With the aid of an integrated inertial navigation algorithm, the proposed north-seeking method can realize such a north-seeking as its accuracy and efficiency are equivalent to those by the four-position method, in which it adopts such a pseudo-observation as the in-situ rotation of IMU is supposed to have limited position and speed variation. Since the pseudoobservation do not require precise IMU angle relative to the base during the whole north-seeking process, the precision angle and angular velocity measurement devices can be essentially eliminated. A large amount of tests (almost 100 groups) indicate that the accuracy can achieve ＜1° within 4 min when using an IMU equipped with fiber optic gyros that have a bias stability of less than 0.5 (°)/h, and the hardware requirement and costs can be significantly reduced compared with that by traditional north-seeking approaches.

north-seeking; Kalman filter; rotation-modulation; pseudo-observation; integrated navigation

U666.1

：A

2015-09-28；

：2015-11-28

中央高校基本科研业务费专项资金资助项目（2042014KF0258）；国家自然科学基金资助项目（41304004，41174028）

牛小骥（1973—），男，教授，博士生导师，从事惯性导航和GNSS/INS组合导航技术研究。E-mail: xjniu@whu.edu.cn

联 系 人：唐健（1981—），男，博士，讲师，从事室内定位与测图研究。E-mail: tangjian@whu.edu.cn

1005-6734(2015)06-0707-07

10.13695/j.cnki.12-1222/o3.2015.06.002