基于Kalman滤波原理对惯导中重力扰动的估计及补偿方法

周 潇，杨功流，王 晶，史 俊，刘元元，李 晶

（1. 北京航空航天大学 仪器科学与光电工程学院，北京 100191；2. 惯性技术国防重点实验室，北京 100191）

基于Kalman滤波原理对惯导中重力扰动的估计及补偿方法

周 潇，杨功流，王 晶，史 俊，刘元元，李 晶

（1. 北京航空航天大学 仪器科学与光电工程学院，北京 100191；2. 惯性技术国防重点实验室，北京 100191）

重力扰动(空间同一点实际重力与正常重力之差，包括垂线偏差和重力异常两部分) 一直是惯性导航系统的重要误差源之一 。随着惯性器件精度的逐步提高，重力扰动所引起的导航误差已成为高精度长航时惯导系统的主要误差之一，不能被忽略，必须对其进行补偿。针对重力扰动误差精确补偿问题，只考虑重力异常的情况，推导并建立了考虑重力异常的惯导误差方程。对误差传播进行了分析，利用Kalman滤波原理设计了带有重力异常状态量的状态方程，并利用GPS和惯导的速度误差作为观测量对重力异常进行滤波并对滤波后得到的重力异常值对惯导重力异常项补偿。进行了2 h的仿真，结果表明：Kalman滤波后可得到当地的重力异常值，重力异常补偿后，速度误差精度可以提高约0.3 m/s，姿态精度提高约0.3′，位置精度提高约150 m。

捷联惯导系统；重力扰动补偿；惯导误差方程；Kalman滤波

惯性导航系统[1]不需要任何外来信息，也不会向外辐射任何信息，仅靠惯性导航系统本身就能在全天侯条件下，在全球范围内和任何介质环境里自主地、隐蔽地进行连续的三维定位和三维定向，具有诸多其他导航系统无法比拟的优点。在惯性导航系统中[2-3]，加速度计组件测量的是比力，比力是载体运动加速度和重力加速度的矢量和。运动加速度是进行导航解算需要知道的加速度，但是，根据 Einstein等价性原理，加速度计是无法区分运动加速度和重力加速度的，需要通过其他手段将比力中的重力加速度扣除，此称为重力补偿。在传统的惯导解算过程中，通常采用通过地球重力场模型得到的正常重力矢量对惯导系统进行重力补偿。正常重力矢量和实际的重力矢量很多情况下是不相等的，二者之差为重力扰动矢量。重力扰动[4]包括正切分量垂直偏差和正交分量重力异常。对于惯性测量传感器而言，一方面它不能辨别重力扰动的垂直偏差和载体实际的水平加速度，使惯性导航系统产生水平速度和位置误差；另一方面，利用包含重力异常的重力数据直接进行惯性导航解算，也将直接引起位置和速度误差。随着惯性器件精度的逐步提高以及高精度捷联惯性导航系统应用需求的提出，重力扰动已经成为高精度捷联惯性导航系统最主要的剩余误差源之一。

本文在只考虑重力异常而不考虑垂线偏差的情况下，对高精度惯性元件的惯性导航系统进行误差分析，推导了带有重力异常作为状态量的Kalman滤波方程[5-6]并进行补偿仿真，分析重力异常引起的系统误差和重力异常补偿后对系统精度的改进效果。

1 考虑重力异常的惯导误差方程

1.1 惯导系统原理图及坐标系定义

惯性导航系统原理图[7]如图1所示。在惯性导航系统中，陀螺仪和加速度计通过稳定平台安装在载体上，分别测量载体相对惯性空间的角运动信息和线运动信息，在给定相关初值和其他必要信息（如重力信息）的情况下，经过一系列运算和控制可以得到载体相对于导航坐标系的位置、速度和姿态等信息。图1中的虚线框表示重力异常对惯性导航系统的补偿，在精度要求不高的传统系统中，这一过程可以忽略。然而，随着惯性器件精度的不断提高和对高精度惯导的需求，讨论和研究惯导的重力扰动补偿越来越具有实际意义。

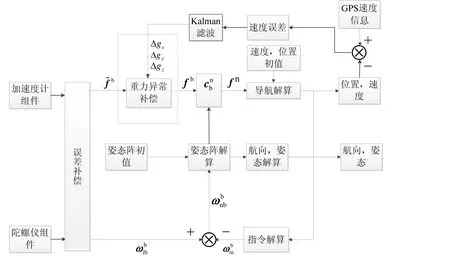
图1 惯性导航系统原理图Fig.1 Principle of inertial navigation system

坐标系定义：b系—载体坐标系，n系—导航坐标系（在本文中取为东-北-天当地水平指北坐标系），e系—地固坐标系，i系—惯性坐标系。

1.2 考虑重力扰动的Kalman滤波方程的推导及建模

捷联惯性导航误差方程[8-9]：姿态误差方程：

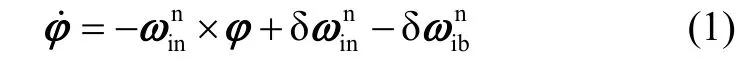
速度误差方程：

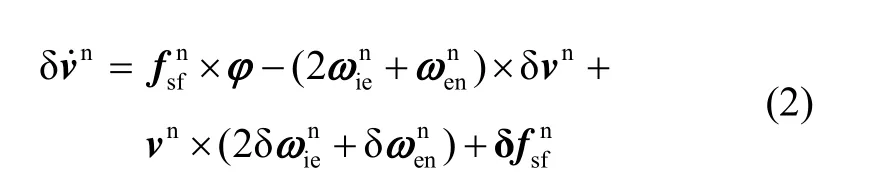
相对位置误差方程：

所以有：

假设陀螺测量误差[10]中包含陀螺标度因数误差δGF、安装误差δGI和陀螺漂移 εb，则有：

同理，假设加速度计测量误差中包含加速度计标度因数误差δAF，安装误差δAI，重力异常 δgn，因为加速度计为高精度加速度计故忽略加速度计零偏▽b，则有：

如果记陀螺误差矩阵δKG为 δKG=δGF+δGI，加速度计误差矩阵δKA为 δKA=δAF+δAI，则有：

顺便指出，陀螺误差矩阵δKG和加速度计误差矩阵δKA可具体展开如下式所示：

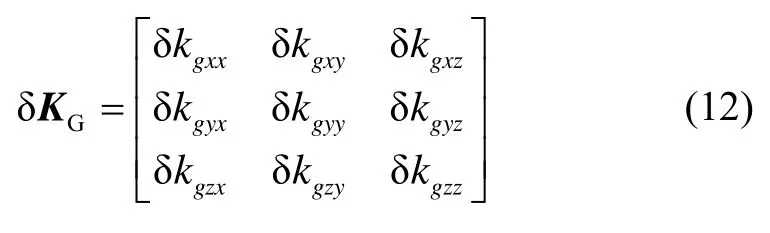
至此，姿态误差方程式(1)经整理改写成：

速度误差方程式(2)经整理改写成：

位置误差方程式(3)经整理改写成：

假设捷联惯组经过严格标定以后陀螺误差矩阵δKG和加速度计误差矩阵δKA均很小，可以忽略它们的影响，建立如下定义15维状态向量[11-12]，其中 φT为姿态角， δvnT为导航坐标系下速度误差， δp为位置误差， εbT载体坐标系下陀螺漂移， δgnT导航坐标系下重力异常。

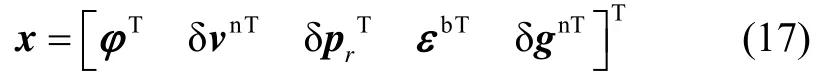
则捷联惯导系统误差方程可表示为

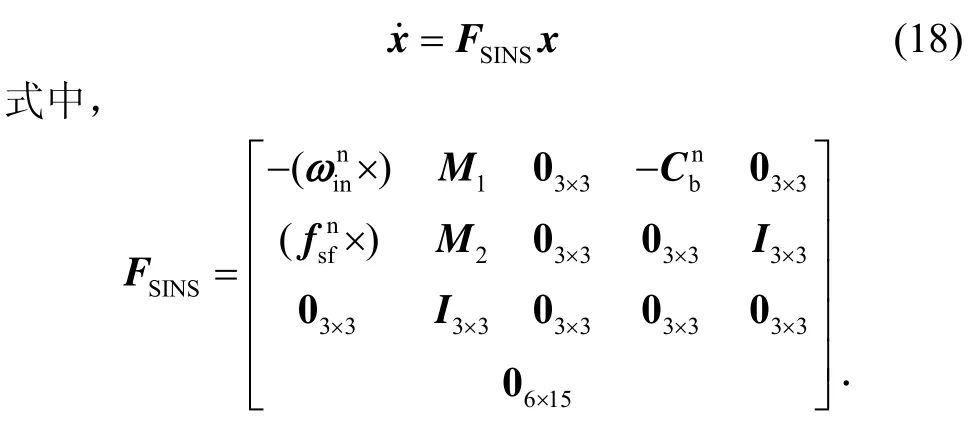
本文中选择GPS和惯导的速度误差作为观测量，有：

2 仿真实验与分析

首先设计飞机飞行轨迹，然后利用飞机运动轨迹发生器模拟飞机运动并产生IMU数据和GPS数据，在所产生的 IMU数据中叠加惯性器件常值漂移。最后，利用本文中所提出的 Kalman滤波方法对轨迹发生器所得出数据进行滤波并将滤波所得重力异常补偿仿真。

2.1 仿真条件

本文在惯导轨迹生成器中引入重力异常，包括重力异常东向分量Δgx、北向分量Δgy、垂直天向分量Δ gz。利用轨迹生成器生成的惯导数据以及GPS数据对系统进行仿真计算。

仿真条件如下：重力扰动东向分量Δgx=10 mGal，北向分量Δgy=20 mGal，垂直天向分量Δgz=30 mGal。三个陀螺的常值漂移均为5×10-5(°)/h，三个加速度计的零偏均为5×10-7g，忽略惯性组件的标度因数误差以及安装误差角。方位初始误差角30′，初始纬度北纬34°，初始经度东经108°，飞机巡航速度50 m/s，巡航时间4 h，先向北飞2 h，转90°再向东飞2 h。仿真步长20 ms。

2.2 仿真结果与分析

使用上述仿真方案的仿真结果如图2至图8所示。

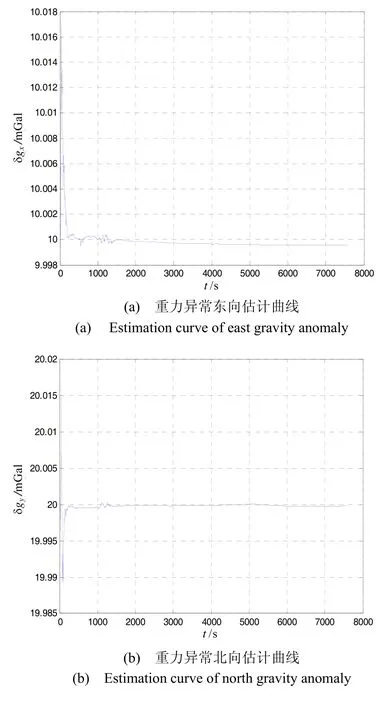
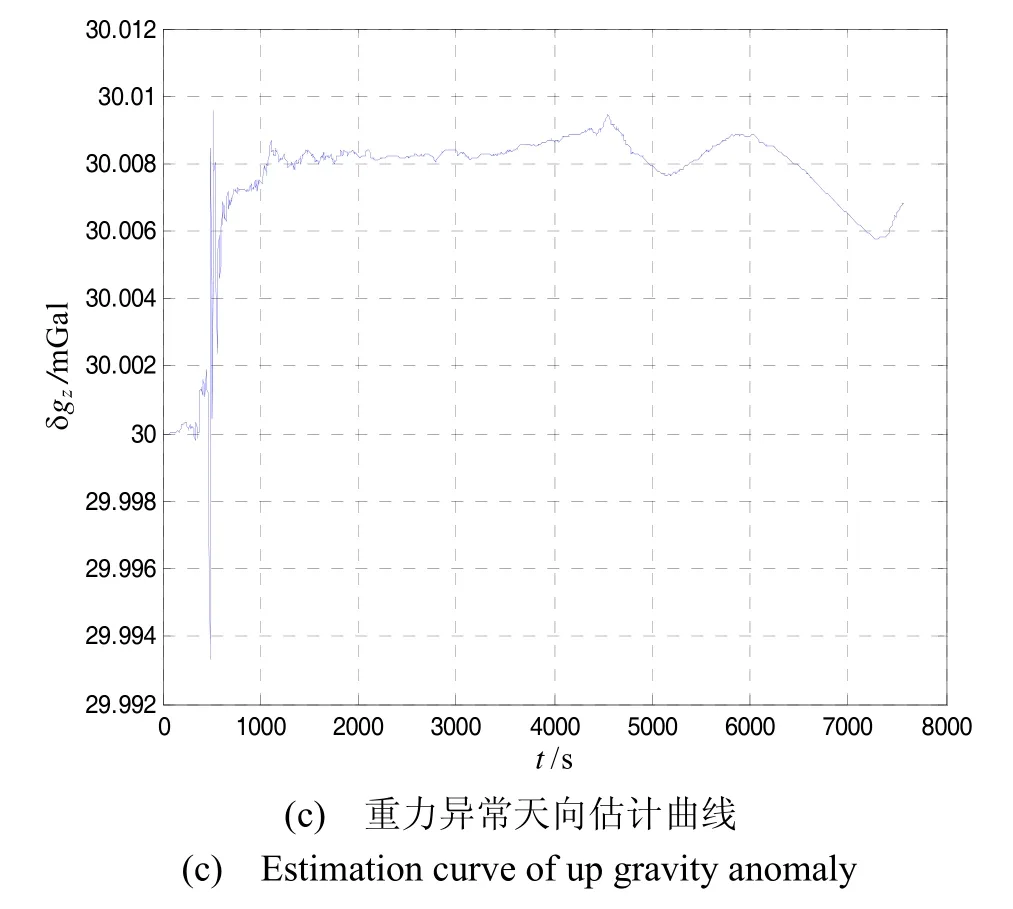
图2 重力异常估计曲线Fig.2 Estimation curve of gravity anomaly

由图2中(a)(b)(c)三图分别可以看出经Kalman滤波后估计出的重力异常东向、北向、天向三个方位的分量值分别为10 mGal、20 mGal、30 mGal。滤波仿真结果与设定值相符，从而验证了Kalman滤波模型的正确性。

对比图3和图4中的姿态误差曲线可以看出在经过重力异常补偿后的惯导系统姿态精度方面有明显提高。经过2 h仿真计算，俯仰角精度能够提高约0.3′，横滚角精度能够提高约0.25′，航向角精度能够提高约0.15′。

对比图5和图6中的速度误差曲线可以看出在经过重力异常补偿后的惯导系统速度精度方面有明显提高。经过2 h的仿真计算，惯导东向速度误差能够提高约0.25 m/s，北向速度误差能够提高约0.06 m/s。

图3 重力异常补偿前姿态误差曲线Fig.3 Error curves of attitude without gravity anomaly compensation

图4 重力异常补偿后姿态误差曲线Fig.4 Error curves of attitude with gravity anomaly compensation

图5 重力异常补偿前速度误差曲线Fig.5 Error curves of velocity without gravity anomaly compensation

图6 重力异常补偿后速度误差曲线Fig.6 Error curves of velocity with gravity anomaly compensation

图7 重力异常补偿前位置误差曲线Fig.7 Error curves of position without gravity anomaly compensation

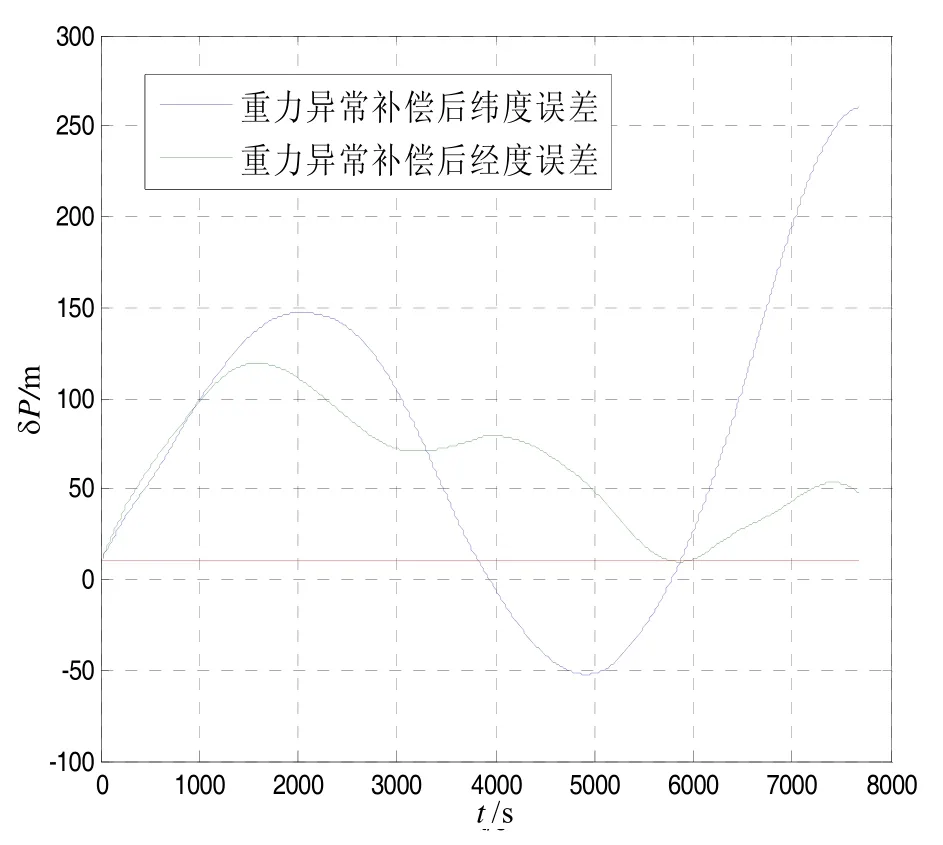
图8 重力异常补偿后位置误差曲线Fig.8 Error curves of position with gravity anomaly compensation

对比图7和图8中的位置误差曲线可以看出在经过重力异常补偿后的惯导系统位置精度方面有明显提高。经过 2 h的仿真计算，惯导纬度误差能够减小约150 m，经度误差能够减小约50 m。

3 结 论

本文基于 Kalman滤波原理对重力扰动关于惯导的误差方程进行推导并建模，用仿真数据对重力异常进行滤波估计并补偿。由上述仿真分析可以形成以下结论：

① 本文所推导设计出的考虑重力异常的 Kalman滤波模型是正确可靠的，经仿真验证可得到实验预期的重力异常值。

② 重力异常补偿后，速度误差精度可以提高约0.3 m/s，姿态精度提高约0.3′，位置精度提高约150 m。

（References）：

[1] 吴太旗, 欧阳永忠, 陆秀平, 等. 重力匹配导航的影响模式分析[J]. 中国惯性技术学报, 2011, 19(5): 559-564. Wu Tai-qi, Ouyang Yong-zhong, Lu Xiu-ping, et al. Analysis on effecting mode of several essential factors to gravity aided navigation[J]. Journal of Chinese Inertial Technology, 2011, 19(5): 559-564.

[2] 卢鑫, 练军想, 吴美平. 高精度舰载惯性导航系统的重力影响研究[J]. 导航与控制, 2010, 9(4): 15-21. Lu Xin, Lian Jun-xiang, Wu Mei-ping. Research on the influence of gravity error compensation on marine inertial navigation system[J]. Navigation and Control, 2010, 9(4): 15-21.

[3] DeGregoria A. Gravity gradiometry and map matching an aid to aircraft inertial navigation systems[D]. Ohio: Air Force Institute of Technology, 2010.

[4] Rummel R, Yi W, Stummer C. GOCE gravitational gradiometry[J]. Journal of Geodesy, 2011, 85: 777-790.

[5] Senobari M. New results in airborne vector gravimetry using strapdown INS/DGPS[J]. Journal of Geodesy, 2010, 84: 277-291.

[6] Li X. Strapdown INS/DGPS airborne gravimetry tests in the Gulf of Mexico[J]. Journal of Geodesy, 2011, 85: 597-605.

[7] 常国宾, 许江宁, 李安, 等. 载体运动对双轴连续旋转调制式惯导方案误差的影响[J]. 中国惯性技术学报, 2011, 19(2): 175-179. Chang Guo-bin, Xu Jiang-ning, Li An, et al. Influence of body dynamics on the error of the scheme of INS with dual-axis continuous autocompensation technique [J]. Journal of Chinese Inertial Technology, 2011, 19(2): 175-179.

[8] Senobari M. New results in airborne vector gravimetry using strapdown INS/DGPS[J]. Journal of Geodesy, 2010, 84: 277-291.

[9] Wang Hu-biao, Wang Yong, Fang Jian. Simulation research on a minimum root-mean-square error rotation-fitting algorithm for gravity matching navigation[J]. Science China: Earth Sciences, 2012, 42(7): 1055-1062.王虎彪, 王勇, 方剑. “最小均方差旋转拟合法”重力辅助导航仿真研究[J]. 中国科学•地球科学, 2012, 42(7): 1055-1062.

[10] Li Shan-shan, Wu Xiao-ping, Ma Biao. Correlative extremum matching algorithm using underwater gravity anomalies[J]. Acta Geodaetica et Cartograpghica Sinica, 2011, 40(4): 464-470.李珊珊, 吴晓平, 马彪. 水下重力异常相关极值匹配算法[J]. 测绘学报, 2011, 40(4): 464-470.

[11] Yuang, Zhang H W, Yuan K F. A Combinational underwater aided navigation algorithm based on TERCOMM/ ICCP and Kalman filter[J]. IEEE Journal of Sciences and Optimization, 2011, 23(1): 952-955.

[12] Man X, Fang J C H, Ning X L. An overview of autonomous navigation for a gravity-assist interplanetary spacecraft[J]. Progress in Aerospace Sciences, 2013, 63: 56-66.

Estimation and compensation for gravity disturbance based on Kalman filtering in inertial navigation

ZHOU Xiao, YANG Gong-liu, WANG Jing, SHI Jun, LIU Yuan-yuan, LI Jing
(1. School of Instrumentation Science and Opto-electronics Engineering, Beihang University, Beijing 100191, China; 2. Science and Technology on Inertial Laboratory, Beijing 100191, China)

The gravity disturbance in inertial navigation system is the difference between the actual gravity and normal gravity on the same point, which includes two parts: deviation of plumb line and gravity anomaly. With the increase of inertial components’ precision, the gravity disturbance becomes one of the major influence factors for the precision of long-time and high-precision inertial navigation system. To compensate this gravity disturbance, we derived and established the inertial navigation error equations by taking into account the gravity anomaly. The propagation of the errors was analyzed, and the state equation considering gravity anomaly is designed based on Kalman filtering. The gravity anomaly of inertial navigation system is compensated by using the velocity difference between GPS and inertial navigation system as view measurement. The simulation is carried out for 2 h, which shows that the gravity anomaly can be correctly calculated by Kalman filtering, and after the compensation, the accuracy of velocity, attitude and position can be improved by about 0.3 m/s and 0.3′ and 150 m, respectively.

SINS; gravity disturbance compensation; inertial navigation error equation; Kalman filter

U666.1

：A

2015-09-05；

：2015-11-29

国家自然科学基金（61340044，11202010）

周潇（1987—），男，博士研究生，从事惯性技术研究。E-mail: Jackzhou002@hotmail.com

联 系 人：杨功流（1967—），男，教授，博士生导师。E-mail: bhu17-yang@139.com

1005-6734(2015)06-0721-06

10.13695/j.cnki.12-1222/o3.2015.06.005