基于逆向导航解算和数据融合的SINS传递对准方法
孙 进,徐晓苏,刘义亭,张 涛,李 瑶
(东南大学 仪器科学与工程学院 微惯性仪表与先进导航技术教育部重点实验室,南京 210096)
基于逆向导航解算和数据融合的SINS传递对准方法
孙 进,徐晓苏,刘义亭,张 涛,李 瑶
(东南大学 仪器科学与工程学院 微惯性仪表与先进导航技术教育部重点实验室,南京 210096)
提出两种观点:1)可以使用一段惯性传感器数据完成捷联惯性导航系统(SINS)的初始对准;2)通过在数据融合中加入逆向—正向SINS解算结果和外部参考数据,可以缩短传感器误差的估计时间。基于以上两观点,旨在不改变卡尔曼滤波器的情况下,短时间内估计陀螺漂移的一种快速传递对准的方法。在一个参考数据更新周期内,储存了惯性传感器数据和参考数据,并且执行了逆向—正向捷联解算。与此同时,当相应的捷联解算结束后,执行数据融合算法。在上述的更新周期内,由于加入逆向—正向捷联解算,陀螺漂移估计操作增加了两次并且缩短了其估计时间。在舰船晃动的情况下,实验表明:与经典的方法相比,当两种方法的数据融合执行次数相等时,提出的方法缩短了对准时间,对准时间从300 s缩短到100 s;当对准时间相等时,方案1的纵摇、横摇和航向对准误差的均值分别为-0.6638、-0.5896、0.3941,其方差分别为1.0736、0.4629、2.1697,而方案2对应的均值和方差分别为-0.4632、-0.5026、0.3375和0.8828、0.3876、1.7289。由此可知,方案2的对准精度高于方案1。
捷联惯性导航系统;传递对准;数据融合;逆向—正向导航解算
初始对准是惯性导航系统的关键技术之一。平台惯性导航系统(GINS)初始对准的基本目的就是使电子机械平台与导航坐标系重合,而 SINS的初始对准是计算载体坐标系与导航坐标系之间的方向余弦矩阵(DCM)。在两种惯性导航系统中,更高的对准精度和更快的对准速度是影响导航精度和武器系统快速反应能力的主要话题。
相比于其他的对准方法而言,传递对准因为其快速性和高精度性而广泛应用于 SINS。1989年,Kain和Cloutier第一个详细阐述了“速度+姿态”的匹配模式[1],正是由于这种匹配模式,传递对准进入了一个快速发展和广泛应用的阶段。他们的测试结果表明:在动基座中,速度+姿态匹配方法在10 s内可以达到1 mrad的精度。
本文在比较GINS和SINS对准过程之后,提出了两种观点。基于这两种观点,设计了一种基于迭代计算的新颖的传递对准方法。仿真实验证明了该方法的有效性,并且在此方法中采用了两种策略来缩短对准时间,提高对准精度和保证对准结果的实时性。
1 基于速度+航向匹配的传递对准方法
1.1 传递对准过程分析
一般情况下,大部分初始对准方法是基于匹配和对比的想法。为了说明这一观点, 以主子惯导之间的传递对准作为一个例子。假设主惯导的导航坐标系为参考导航坐标系:如果平台式惯性导航系统作为子惯导,则电子机械平台作为失准导航坐标系,如图 1(a)所示的坐标系 p;如果捷联式惯性导航系统作为子惯导,则数学平台作为失准导航坐标系,如图1(b)所示的坐标系n′。当失准坐标系与参考坐标系不重合时,将会出现传感器数据(p坐标系的传感器数据或者投影到n′系的传感器数据)和导航解算方案的差异。在惯导解算的过程中,导航坐标系的初始失准角、速度误差和传感器偏差将会导致失准角,并进一步生成传感器数据之间的导航参数的差异。
在传递对准中,状态向量(如失准角和陀螺漂移)基于最优估计理论的 Kalman波器(或其它数据融合滤波器)可以将其估计出 。在此对准方法中,上述的差作为测量向量,误差传播方程作为系统方程,测量向量和状态向量之间的数学关系作为测量方程。当使用校正模式时,上述的估计可以用于随后的导航解算。例如失准角估计和速度误差可以返回重置或修正DCM 和速度,传感器偏差估计可用于补偿传感器数据。当消除上述的差异或者使其足够小时,利用比较、估计和校正,传递对准可以满足条件。

图1 INS对准过程Fig.1 Alignment process for INS
1.2 基于“速度+航向”匹配的传递对准模型
1.2.1 系统方程
选取速度误差、失准角和陀螺漂移作为系统的状态向量:

式中:δVE和δVN分别为东向和北向速度误差;Eφ、Nφ和Uφ为失准角的纵摇、横摇和航向;xε、yε和zε为x、y和z轴的陀螺漂移。对应行驶在海上的船而言,高度和天向速度可以置零。
系统状态方程可以表示如下:

式中:A(t)是状态矩阵;W(t)是系统噪声矩阵。利用系统向量、速度误差和失准角方程,状态矩阵A(t)可以表示如下[2]:

式中,VE和VN为相应的东向和北向速度,ωie和R分别是地球自转角速度和半径,L是舰船位置的纬度,fE、fN和 fU是加速计测量数据 fb在导航坐标系n上的投影,Tij(i, j=1,2,3)是主惯导的方向余弦矩阵。
1.2.2 量测方程
对准过程中主子惯导速度和航向之差作为量测向量:

式中:VE、 VN和Y是子惯导的东向速度、北向速度和航向;VME、 VMN和YM为相应主惯导的东向速度、北向速度和航向。当考虑到传递对准中的主要问题,比如杆臂效应、挠曲变形和时间延迟, VME、 VMN和YM应该作为补偿信息。以杆臂效应补偿为例,当使用速度匹配时,杆臂速度应该加到主惯导速度中去,并且只有该组合的速度可以作为外部参考导航参数。因此,VMi(i= E, N)可以表示如下[2]:

式中:VM0E、VM0N分别为主惯导的东向速度和北向速度;VarmE、VarmN分别为杆臂速度投影到东向和北向的速度。
本文的目的是获得一种相对于传统的传递对准提高对准精度并且缩短对准时间的方法,而不是杆臂效应、挠曲变形和时间延迟的补偿方法。然而,当考虑到上述问题,存储的外部参考导航信息应该作为补偿的参数,如: VME=VM0E+VarmE。
系统的量测方程可以表示如下:

式中:H(t)是量测矩阵;V(t)是量测噪声矩阵。
根据量测矩阵和状态矩阵之间的关系,量测矩阵H (t)可以表示如下:

2 传递对准的进一步分析
2.1 传感器数据与失准角之间的关系
为方便起见,以静基座下加速度测量值和失准角之间的关系为例。在平台惯性导航系统中,惯性传感器是安装在如图 1(a)所示的电子机械平台上的。水平失准角引起的水平重力耦合加速度可以利用水平方向的加速度计来测量,并且传感器数据和失准角之间的关系如下所示:

在上述耦合的过程中,没有考虑到传感器的偏置,传感器数据是由失准角的值决定的。也就是说平台惯性导航系统中的传感器数据和失准角之间没有直接关系。
但是如图1(b)所示,惯性传感器安装在捷联惯性导航系统的载体坐标系上,所以只有当传感器数据投影到数学平台上之后才可以进入初始对准。传感器测量数据和投影的传感器数据的关系如下:


式中,▽E和▽N分别是东向和北向的等效加速度计偏置。
另外,不同于 GINS,数学平台没有质量、阻尼和弹簧,因此导航坐标系的调整可以立即取得效果而无需考虑像GINS中的机械平台的转动。
上述的这些特性为缩短对准时间和提高对准精度提供了一个潜在的方法。
2.2 缩短对准时间和提高对准精度潜在的方法
以图2所示的导航解算和传递对准为例。该例子包括导航解算、传递对准数据融合和闭环校正模式三个子过程,第1.2节已经给出数据融合过程的细节。
2.2.1 SINS导航解算一般算法
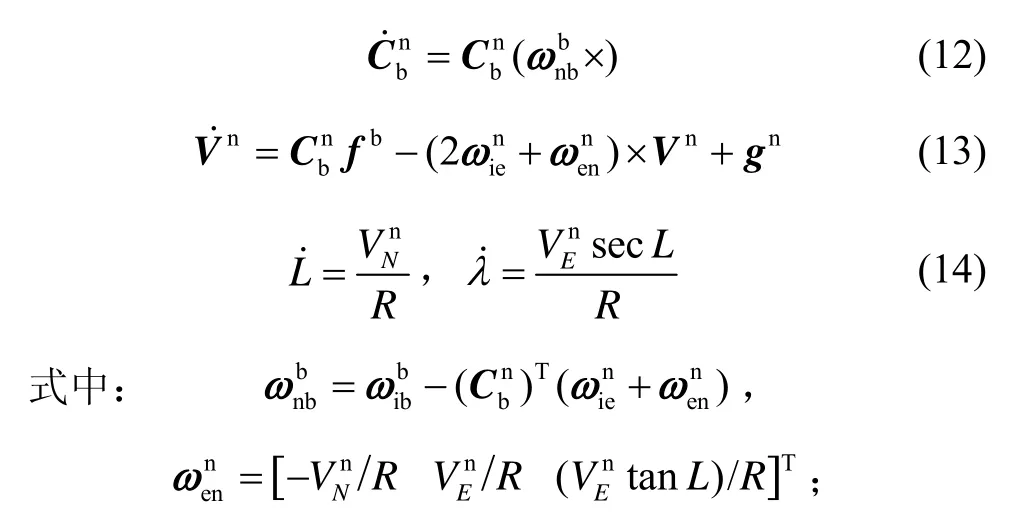
因为计算机的递推更新,在一定得采样周期和导航解算更新周期内,式(12)~(14)的SINS导航解算一般算法要转化为离散形式。对于总是处在低动态的舰船而言,可以采用单一的采样解算算法,也就是每段导航周期都只采用一段采样的传感器数据。假设上述的采样时间都等于Ts,然后导航解算一般算法的离散形式可以表示如下:

式中,k表示递推周期。
2.2.2 SINS逆向解算算法
如图2所示,在逆向解算过程中,舰船需要从终点返回到原点。因此在正常的过程中,所有的传感器数据必须保存。根据导航解算一般算法的离散形式,此逆向解算过程可以表示如下[2-7]:
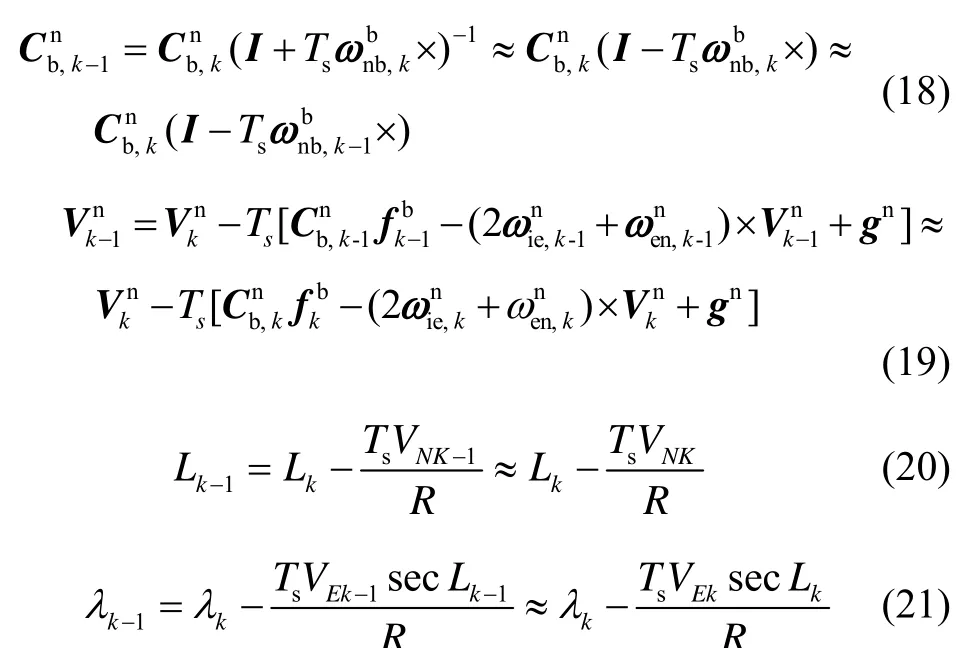
式中,k从n逐渐递减为0。如图2所示,tn1既是时间段tn1~t01的起始点也是时间段t0~tn的终点。以tn时刻的姿态、速度和位置作为tn1时刻的初始姿态、速度和位置,则完全实现逆向解算了。在时间段t0~tn和tn1~t01,相同的递推周期,舰船拥有一样的姿态、速度、位置以及相同的加速度但是不同的方向。在式(18)~(21)求近似解时,一些误差被引入其中。当迭代周期足够短时,所有的这些误差可以忽略。
逆向解算之后,为了使舰船从原点到终点需要进行正向导航解算,导航解算一般算法的离散形式可以作为正向导航解算算法。
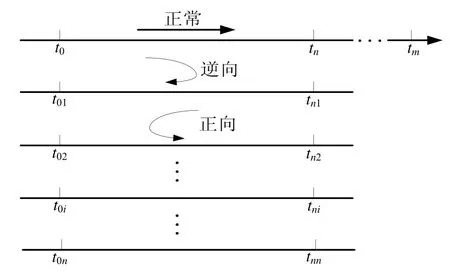
图2 SINS逆向—正向导航解算过程Fig.2 Resolution process of backward-forward SINS
3 基于数据存储与循环解算的快速传递对准
上述步骤表明,SINS对准可以使用一系列数据来完成。在此步骤中,为了缩短对准时间,我们将Kalman滤波器与逆向—正向SINS解算算法相结合。
如图3所示,将基于Kalman滤波传递对准模型和闭环修正方法运用于快速传递对准算法中。闭环修正意味着数据融合之后,速度误差和失准角的重新估计值将会被带入SINS来修正对应的参数,陀螺漂移新估计值将会作为下一步导航解算的新的补偿值。换句话,当数据融合之后,数学平台姿态矩阵C将会得到修正。对舰船而言,主惯导参考数据的更新频率低于子惯导导航解算的频率,Ts和Tn分别作为导航解算和参考数据的更新周期,即令Tn为逆向-正向SINS解算周期。
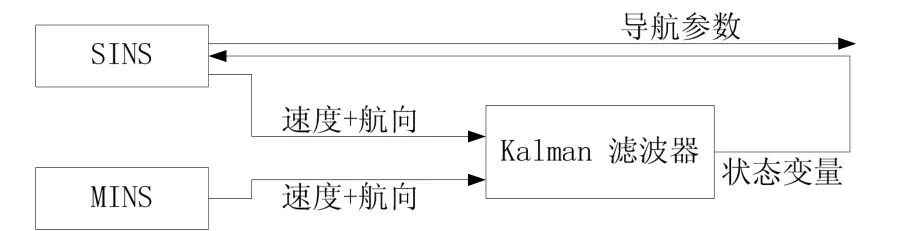
图3 Kalman滤波器Fig.3 Kalman Filter
比较两种传递对准的方式,图4简要介绍了陀螺漂移的估计过程,(a)和(b)分别指两种对准方式对应的陀螺漂移的估计过程,(a)中没有使用逆向—正向SINS解算和数据融合算法,而在(b)中都使用了。图4中虚线指实际的陀螺漂移,实线指陀螺漂移的估计值。运用 Kalman滤波器和上面步骤中介绍的匹配方法,陀螺漂移的估计是一个缓慢的过程,一段长时间后此过程将会收敛于真实的陀螺漂移[8]。
如图 4(a)所示,当参考数据有效时,比如在tn时刻,数据融合被执行。随着对失准角和速度误差的重新估计,初始导航参数将会作为下一阶段的迭代参数,比如tn~t2n,意味着数学平台n′系将会被修正,并且陀螺漂移新的补偿值也将会重置。随着时间的推移,在每个参考数据更新周期,此方法中数据融合会运行。
但是如图4(b)所示,在相同的参考数据更新周期内(比如t0~tn),在tn时刻将会运行数据融合并且产生新的估计,因此新的初始导航参数也随之产生。在t01时刻将会产生新的导航初始参数和对陀螺漂移新的补偿值,这些都是不同于t0时刻的。因此在t01时刻将会产生新的估计,因为t0时刻和t01时刻的Kalman滤波器的量测向量是不同的,所以此估计不同于t0时刻。类似地,tn2时刻获得的新的信息也是不同于tn时刻的。在图4(b)中,因为加入了逆向—正向SINS解算和数据融合,陀螺漂移估计和数学平台n′的调整将会多执行两次。在第二种方法中,尽管与第一种方法有相同的可观测性,但由于增大了估计频率,所以缩短了估计时间。

图4 陀螺漂移的估计过程Fig.4 Estimation process for gyro bias
4 仿真与分析
4.1 仿真参数
假设舰船处在海况比较差的环境下,舰船的晃动参数如表2所示,令舰船的初始姿态为0且假设舰船没有线性运动,所处位置为北纬32°,东经118°。初始姿态角分别设为 1°、-1°和 3°。东向速度、北向速度以及方位的白噪声方差分别为(0.4 m/s)2和(0.3°)2。
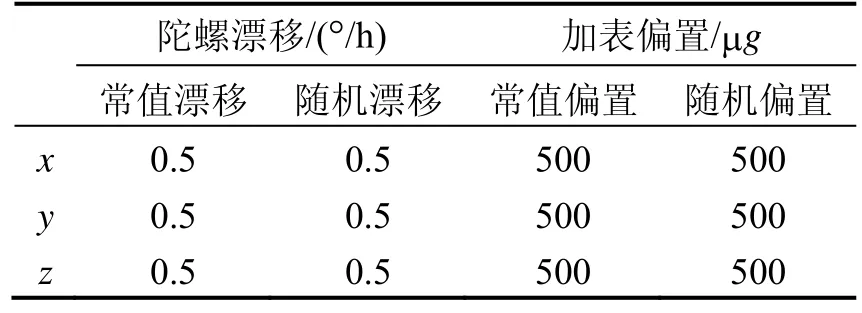
表1 传感器误差Tab.1 Sensor error
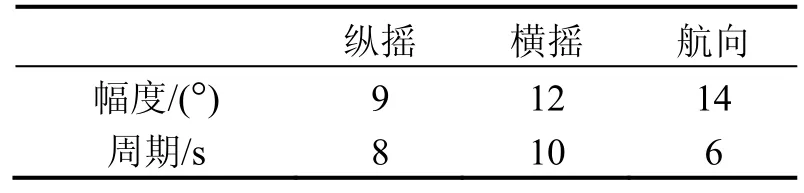
表2 转台晃动参数Tab.2 Swinging parameters of the turntable
Kalman滤波器的参数设置如下:

对两种数据融合方案进行了比较。方案一是经典的传递对准方法,即没有加入循环解算算法;方案二是加入逆向—正向SINS解算和数据融合的传递对准。这两种方案的传递对准模型都是基于速度+航向匹配的。
传感器采样周期和导航解算周期Ts都设置为 10 ms,主惯导参考数据采样周期设为1 s。由第三节分析可知,在每个参考数据周期内,方案2中的导航解算将会被执行300次,数据融合将执行3次,而在方案2中的导航解算将会被执行100次,数据融合只执行1次。
“速度+航向”匹配的方法中,加速度的偏置是不可观测的[9],因此假设传感器误差如表 1所示,纵摇和横摇的对准精度范围在-0.4990 mrad到0.4990 mrad之间,相应地,航向对准精度为0。
4.2 仿真结果及分析
仿真时间为 1100 s,每秒存储一次仿真结果。失准角误差曲线如图5所示,速度误差曲线如图6所示,陀螺漂移估计曲线如图7所示。图5和图6中虚线是失准角和速度对准精度的界限。图7的虚线指的是陀螺常值漂移的设定值。
如图5的曲线所示,船在小幅度的晃动频率下,不管是方案1(scheme1)还是方案2(scheme2),都能快速地估计出失准角。但是从失准角曲线的趋势看,尤其是横摇误差曲线,方案2的估计速度明显高于方案1。图6的曲线表明,方案1和方案2的速度误差估计速度和精度大体相等。
图7所示的曲线表明,方案2的x、y、z方向陀螺漂移估计分别需要80 s、100 s、220 s,而方案1所需时间分别为180 s、200 s、900 s。

图5 失准角误差估计Fig.5 Estimation for misalignment angels
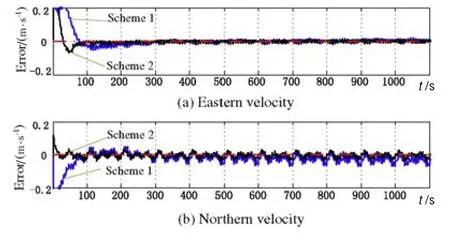
图6 速度误差估计Fig.6 Estimation for velocity errors
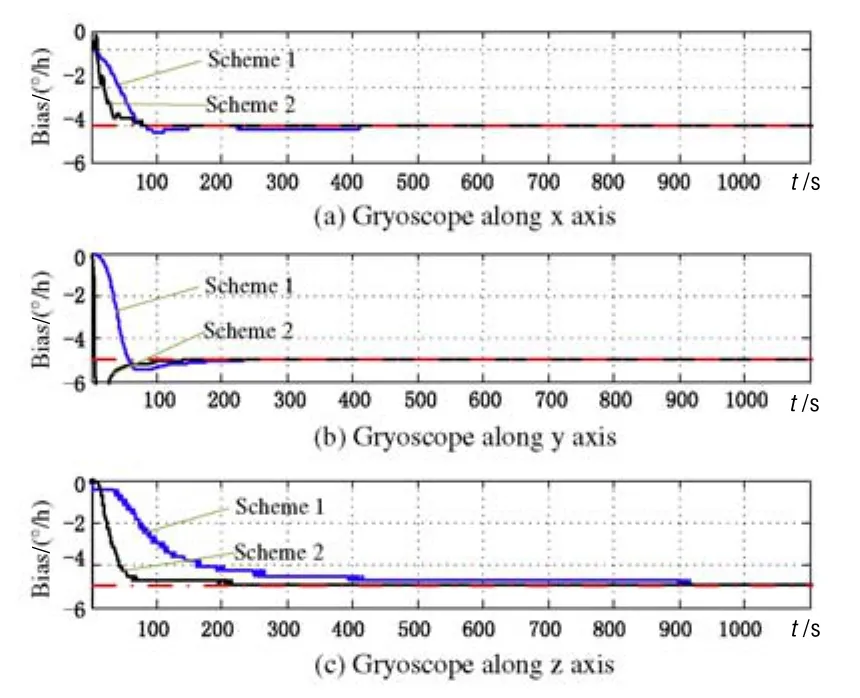
图7 陀螺漂移估计Fig.7 Estimation for gyro drift
5 结束语
本文提出了两种观点。第一种观点是:SINS的数学平台切断了传感器数据和失准角之间的关系,这就意味着可以利用一段相同的传感器数据进行重复解算来完成初始对准。第二种观点是:在相应的解算结果和外部数据中加入逆向—正向捷联解算和数据融合算法,大大地减少了对准时间。
运用上面两种观点,详细设计了逆向—正向捷联解算算法。同时详细设计了快速传递对准算法,在此算法中,将逆向—正向捷联解算和两次陀螺漂移估计加入到一个参考数据更新周期中。仿真结果表明:相比于没有加入逆向—正向捷联解算和数据融合的传递对准而言,本文提出的方法的对准时间从300 s缩短到100 s。
(References):
[1] Kain J E, Cloutier J R. Rapid transfer alignment for tactical weapon applications[C]//AIAA Guidance, Navition and Control Conference. 1989: 1290-1300.
[2] Liu X, Xu X, Liu Y, et al. A fast and high- ccuracy transfer alignment method between M/S INS for ship based on iterative calculation[J]. Measurement, 2014, 51: 297-309.
[3] Liu X, Xu X, Wang L, et al. A fast compass alignment method for SINS based on saved data and repeated navigation solution[J]. Measurement, 2013, 46(10): 3836-3846.
[4] Qin F, Li A, Xu J. Improved fast alignment method of strapdown INS using bidirectional processes and denoising[J]. Journal of Chinese Inertial Technology, 2014, 22(4): 453-458.
[5] He H, Xu J, Li J, et al. Improved fast backtracking alignment approach for strapdown inertial navigation system[J]. Journal of Chinese Inertial Technology, 2015, 23(2): 179-183.
[6] 李京书, 许江宁, 何泓洋, 等. 严格逆向过程的罗经回溯对准方法[J]. 系统工程与电子技术, 2014, 36(2): 348-353. Li Jing-shu, Xu Jiang-ning, He Hong-yang, et al. Backtracking scheme for alignment with strict reverse process based on compass[J]. Systems Engineering and Electronics, 2014, 36(2): 348-353.
[7] 刘锡祥, 徐晓苏, 李天旦, 等. 基于数据存储与循环解算的SINS 快速对准方法[J]. 中国惯性技术学报, 2013, 21(6): 715-720. Liu Xi-xiang, Xu Xiao-su, Li Tian-dan, et al. Fast alignment method for SINS based on stored data and loop calculation[J]. Journal of Chinese Inertial Technology, 2013, 21(6): 715-720.
[8] 朱立华, 程向红, 何应云. 传递对准中滤波器的收敛判据[J]. 中国惯性技术学报, 2011, 19(3): 277-285. Zhu Li-hua, Cheng Xiang-hong, He Ying-yun. Filter convergence criterion in transfer alignment[J]. Journal of Chinese Inertial Technology, 2011, 19(3): 277-285.
[9] 秦永元. 惯性导航[M]. 科学出版社, 2014.
[10] 周本川, 程向红, 刘道静. 基于谱分解的 SINS 传递对准可观测度分析方法[J]. 中国惯性技术学报, 2010, 18(5): 518-522. Zhou B C, Cheng X H, Liu D J. Analysis method of observable degree based on spectral decomposition in SINS transfer alignment[J]. Journal of Chinese Inertial Technology, 2010, 18(5): 518-522.
Transfer alignment method for SINS based on reverse navigation solution and data fusion
SUN Jin, XU Xiao-su, LIU Yi-ting, ZHANG Tao, LI Yao
(Key Laboratory of Micro-inertial Instrument and Advanced Navigation Technology of Ministry of Education, School of Instrument Science and Engineering, Southeast University, Nanjing 210096, China)
Two viewpoints are presented: 1) we can use a set of inertial sensor data to complete the initial alignment of strapdown inertial navigation system (SINS); 2) by adding the results of backward-forward SINS navigation solution and external reference data into data fusion, the estimation time of the sensor error can be shortened. Based on these viewpoints, a rapid transfer alignment method without changing the Kalman filter is introduced to estimate the gyro drift in a short time. In one reference data update cycle, the inertial sensor data and reference data are stored, and the backward-forward SINS solution is executed. Meanwhile, data fusion algorithms are performed after finishing the corresponding SINS solution. In the above update cycle, due to the addition of backward-forward SINS solution, the operation of gyro drift increases twice and its estimation time is shortened. The experiment on a shaking ship shows that the alignment time is shorten to 100 s by the proposed method, which is reduced by 3 times compared with that by the classical method, if the two methods takes equal time for data fusion. In situation that the two schemes take equal alignment time: the mean errors of pitch, yaw and heading alignment by scheme one are -0.6638, -0.5896, and 0.3941, respectively, and the variances are 1.0736, 0.4629, and 2.1697, respectively, while in scheme two, the mean errors are -0.4632, -0.5026, 0.3375, and the variances are 0.8828, 0.3876, 1.7289, showing that the alignment accuracy of the scheme two is higher than that of the scheme one.
SINS; transfer alignment; data fusion; backward-forward navigation solution
U666.1
:A
2015-09-28;
:2015-11-16
国家自然科学基金项目(61473085,51175082,51375088,61273056)
孙进(1988—),男,博士研究生,从事组合导航研究。E-mail: sunjin8607986@126.com
联 系 人:徐晓苏(1961—),男,教授,博士生导师。E-mail: xxs@seu.edu.cn
1005-6734(2015)06-0727-06
10.13695/j.cnki.12-1222/o3.2015.06.006

