基于虚拟样机的弹药装填机械臂动力学分析与仿真

罗建华， 徐 达

(装甲兵工程学院兵器工程系， 北京 100072)

基于虚拟样机的弹药装填机械臂动力学分析与仿真

罗建华， 徐 达

(装甲兵工程学院兵器工程系， 北京 100072)

在新型弹药装填机械臂虚拟样机的基础上，对弹药装填机械臂静力学进行了详细求解，得到其数学解析式；采用拉格朗日能量平衡法构建了弹药装填机械臂系统动力学模型，在ADAMS环境下对其进行了动力学仿真分析，得到了弹药装填机械臂关节的角度、力及力矩参数特性曲线，为弹药装填机械臂实时控制奠定了基础，同时也为其机构设计优化提供了依据。

弹药装填机械臂；动力学分析；虚拟样机

大口径火炮弹药自动装填系统是联系坦克和自行火炮弹药弹仓单元和火炮发射单元的重要环节，能够在计算机控制下有效代替弹药装填手实现弹药的快速装填，是提高坦克和自行火炮战斗力及生存能力的关键技术[1]。目前,世界各国所采用的坦克和自行火炮弹药自动装填系统均是多机构串联式机电系统，部件多，结构复杂，可靠性低，大幅改进的潜力不足，难以满足未来大口径火炮系统对弹药自动装填的需求。弹药装填机械臂具有智能化、自适应性以及在复杂工况下自主工作等优势，能够有效满足顶置炮等未来大口径火炮的弹药自动装填需求，是大口径火炮弹药自动装填系统未来的发展方向。

针对未来大口径火炮的弹药自动装填需求，笔者设计了弹药装填机械臂，通过各臂杆的协调运动实现了弹药供输。要使弹药装填机械臂完成复杂非线性弹药供输工作流程，必须对弹药装填机械臂运动轨迹进行实时准确控制，因此需要对弹药装填机械臂进行动力学仿真分析，得到每个关节的角度、力、力矩及其变化规律。针对当前牛顿-欧拉法、高斯法、凯恩法、拉格朗日法、阿贝尔方法、旋量法等动力学分析方法应用于弹药装填机械臂存在的问题[2-6]，笔者将拉格朗日能量平衡法应用于弹药装填机械臂的动力学分析，较好地解决了弹药装填机械臂的关节控制参量解算问题，为弹药装填机械臂实时控制奠定了基础，同时也为弹药装填机械臂的结构优化提供了依据。

1 弹药装填机械臂静力学分析

1.1 弹药装填机械臂的结构模型

弹药装填机械臂结构及连杆坐标系如图1所示，可见：弹药装填机械臂由腰部、大小臂、腕部及末端执行器4大部分构成，为PRRR-S型结构，其中，P为移动副，R为转动副，S为球面关节[7]。

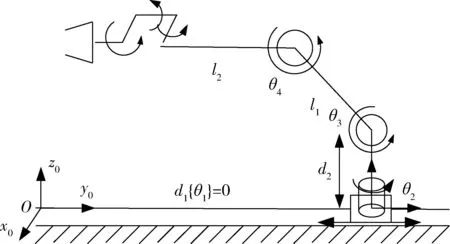
图1 弹药装填机械臂结构及连杆坐标系

1.2 弹药装填机械臂静力学分析

弹药装填机械臂静力学分析是进行动力学仿真的前提。弹药装填机械臂受力分析如图2所示。

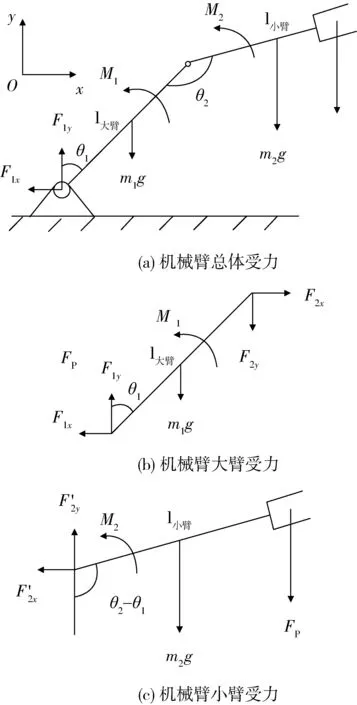
图2 弹药装填机械臂受力分析

静力学平衡方程为

(1)

式中：Fx、Fy分别为x、y方向上的力；Mi为节点i处的力矩。

系统的力和力矩方程为

(2)

式中：m1、m2分别为大、小臂杆件的质量；l2、l1分别为大、小臂杆件的长度；FP为弹药装填机械臂手腕结构上部受力，为弹药与手腕结构所受重力之和；θ1为大臂与竖直方向夹角；θ2为大、小臂之间夹角；M1、M2分别为大、小臂上所受力矩。

小臂杆件的力和力矩方程为

(3)

联立式(2)、(3)可得

(4)

2 弹药装填机械臂动力学模型的建立

多关节的弹药装填机械臂的每一个关节都可以在电机驱动之下独立运动，该系统属于复杂的动力学耦合系统，其数学模型具有明显的非线性和复杂性[8]。笔者在试用动力学分析方法时发现：牛顿-欧拉法需要解决弹药装填机械臂关节处的约束反力，消去形成弹药装填机械臂运动和驱动关系的显式较烦琐，且不能直接获取动力学方程的解析式，得不到弹药装填机械臂动力学分析的整体概念；联合使用凯恩法和旋量法，虽然形式较简单，但存在大量复杂的矩阵运算，对计算机运算速度要求较高；而拉格朗日法能直接获取各关节点的速度和加速度，非常适于描述弹药装填机械臂中不可逆转的混沌现象。因此，本文选用基于能量平衡的拉格朗日方法,来解决弹药装填机械臂的关节控制参量解算问题。

弹药装填机械臂的总动能K与总势能P分别为

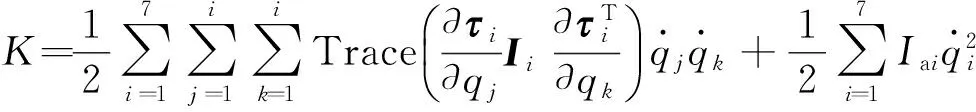
(5)

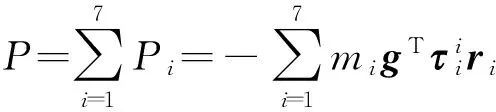
(6)

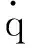
对于弹药装填机械臂连杆系统，拉格朗日函数L定义为系统总动能K与总势能P之差，即

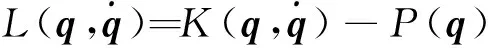
(7)

式中：q=(q1,q2, …,q7)T。

由式(5)-(7)及弹药装填机械臂结构，得到其动力学方程为

式中：Dij为关节i、j之间的相互耦合惯量；Dijk为由关节j、k的速度所造成的作用在关节i上的哥氏力；Di为作用在关节i上的重力负载。

3 弹药装填机械臂动力学仿真

3.1 刚体定义

根据弹药装填机械臂的几何结构和材质属性，确定其各杆件的质量、转动惯量属性如表1所示[9]。其中刚体编号i=1,…,7分别代表弹药装填机械臂的基座、基座横移段、腰部、大臂、小臂、腕部及末端执行器。

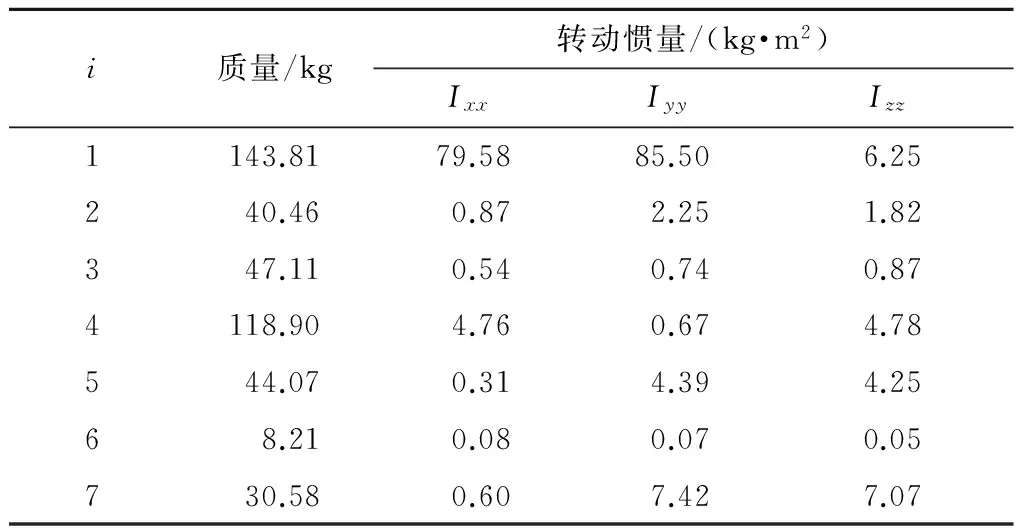
表1 刚体属性

3.2 驱动定义

针对弹药装填机械臂供输弹作业任务，采用step(time,x0,h0,xt,ht)流程函数定义驱动,其中:

x0为初始时间；h0为自变量初始值；xt为终止时间；ht为自变量结束值。弹药装填机械臂轨迹规划流程函数如表2所示。

表2 流程函数

3.3 仿真与分析

在ADAMS中设置仿真参数，利用PostProcessor处理模块，按照弹药装填机械臂动力学方程(8)施加约束和外力[10]，如图3所示。

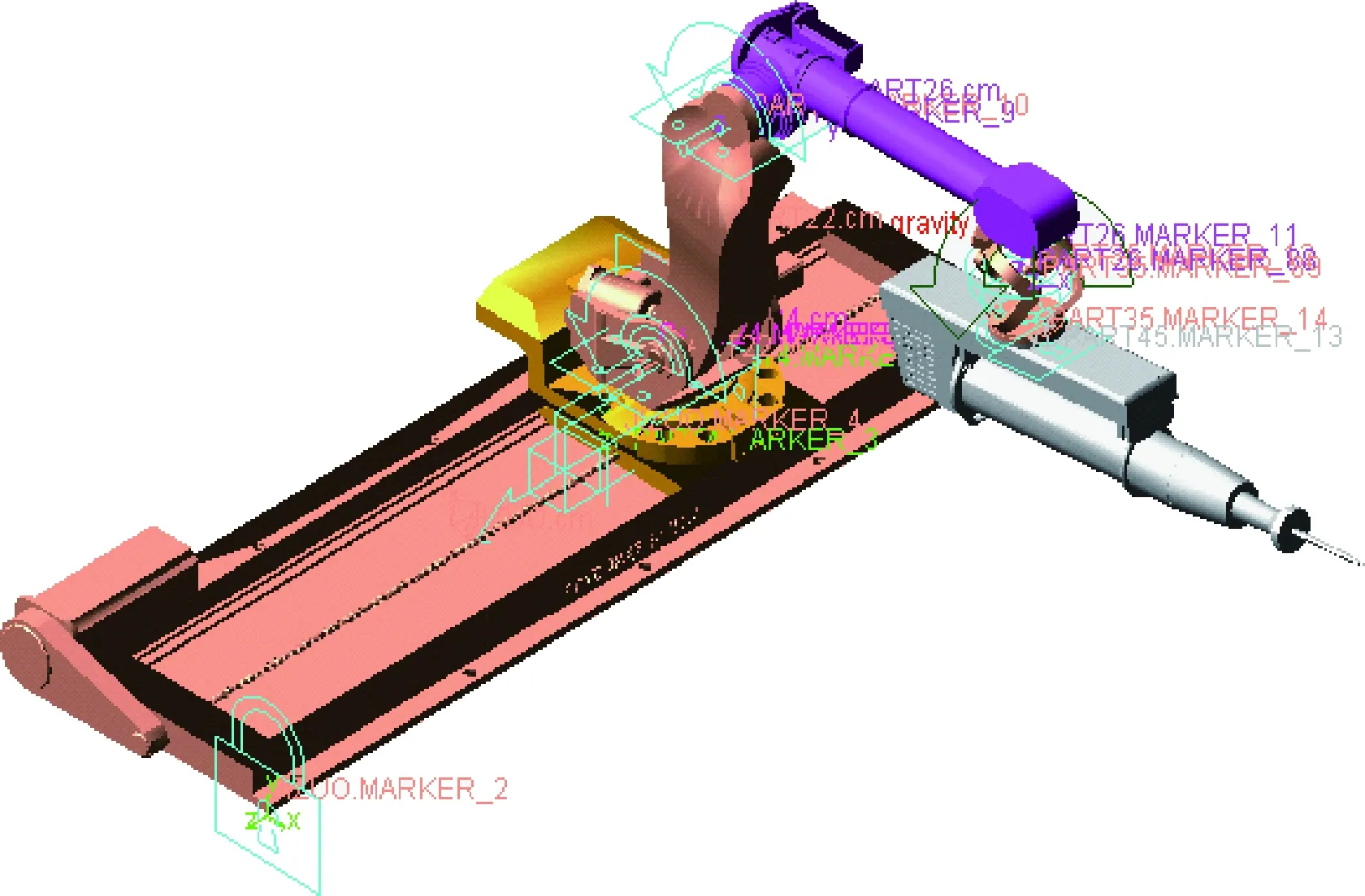
图3 弹药装填机械臂动力学模型

根据已定义的变量和参数，进行动力学仿真分析，得到弹药装填机械臂各关节的角度、力及力矩参数特性曲线，以肩关节θ3为例，仿真结果如图4-6所示。

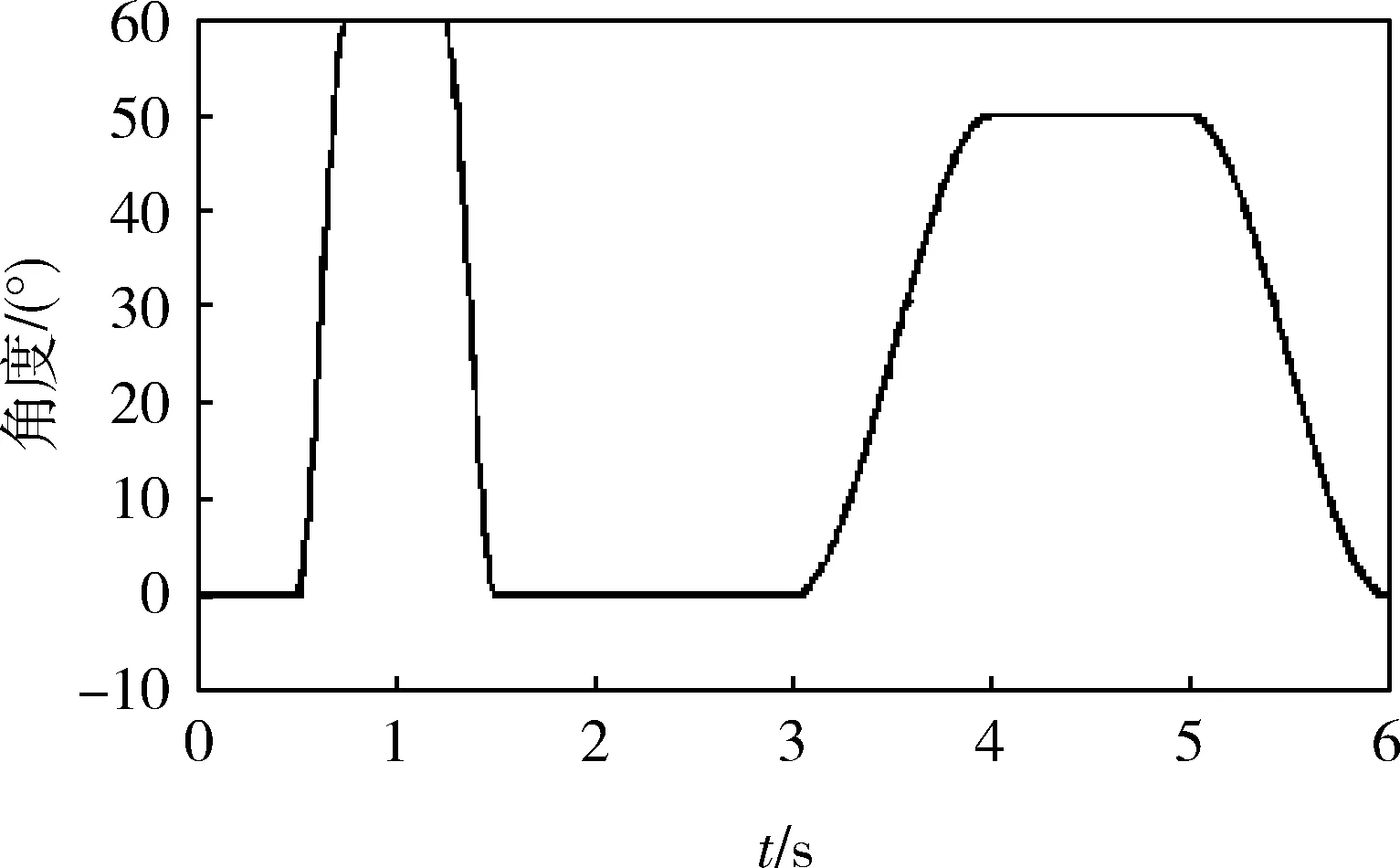
图4 关节3角度测量曲线

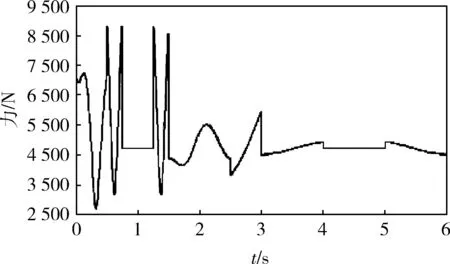
图5 关节3受力曲线

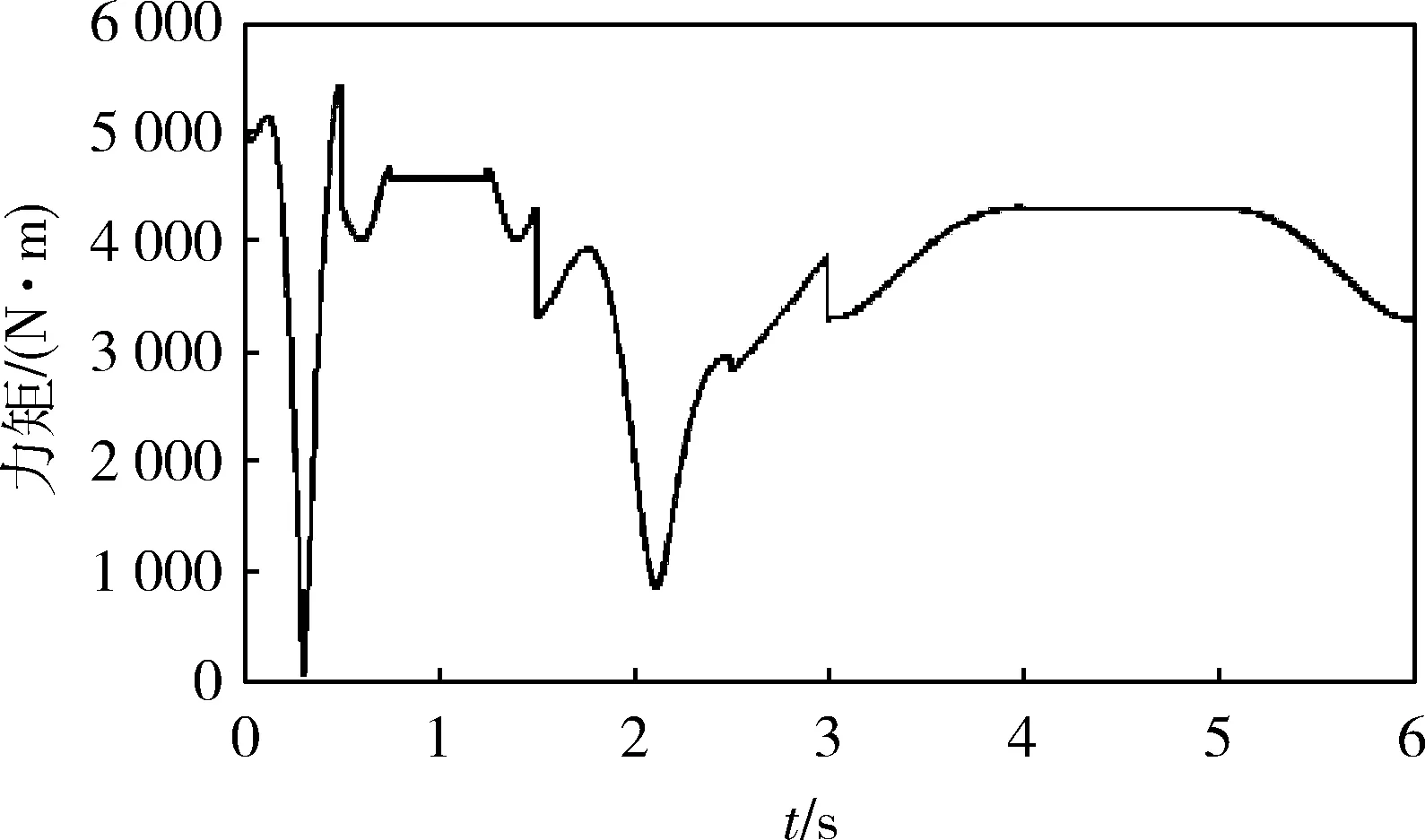
图6 关节3所受力矩曲线

从图4可以看出：肩关节θ3最大转角在关节变量范围内，同时，肩关节处转角曲线在某些时刻左右斜率表现出不一致，这说明此时的角速度、角加速度存在突变，需要通过调整弹药装填轨迹、优化驱动函数进行改善。从图5、6可以看出：力和力矩曲线函数存在许多小的峰刺，且在开始时刻曲线变化较为剧烈，多次达到峰值，这主要是由关节启动时瞬时加减速过大造成的，外在表现就是关节的不必要振动，可在轨迹规划时考虑平滑过渡。

综合图4-6的仿真曲线可知：所得仿真结果符合弹药装填机械臂作业任务要求，同时也表明所构建的动力学模型是正确的。

4 结论

本文对弹药装填机械臂进行了静力学分析，基于能量平衡的拉格朗日法建立了弹药装填机械臂的动力学模型，通过动力学仿真得到了弹药装填机械臂关节的角度、力及力矩参数特性曲线，为弹药装填机械臂实时控制奠定了基础。但弹药装填机械臂的力和力矩曲线存在较大的波动与峰刺，下一步将对弹药装填机械臂的结构优化和装填轨迹规划进行深入研究，以进一步提高弹药装填机械臂的弹药装填作业平稳性，满足未来大口径火炮的弹药自动装填需求。

[1] 徐达, 夏祥, 李华, 等. 弹药装填机器人作业平台仿真系统设计与实现[J]. 装甲兵工程学院学报, 2012, 26(5): 55-58.

[2] 韩佩富, 王常武, 孔令富, 等. 改进的6-DOF并联机器人Newton-Euler动力学模型[J]. 机器人, 2000, 22(4): 315-318.

[3] 宋伟刚．机器人学：运动学、动力学与控制[M]. 北京: 科学出版社, 2007.

[4] 孙树栋. 工业机器人技术基础[M]. 西安：西北工业大学出版社,2006: 92-119.

[5] 罗阿尼．大中口径舰炮敏捷供弹系统设计及虚拟样机研究[D]．哈尔滨: 哈尔滨工业大学, 2005.

[6] 郭希娟, 彭艳敏, 耿清甲. LR-Mate机器人动力学性能分析[J]. 机械工程学报, 2008,44(10): 123-128.

[7] 徐达, 王中盛, 刘广洋, 等. 基于串并联结构的弹药装填机械臂设计[J]. 装甲兵工程学院学报, 2008,22(5): 45-50.

[8] 徐达, 帅元, 郝琢, 等. 弹药装填机械臂自适应PD控制算法[J]． 装甲兵工程学院学报, 2011,25(1): 49-53.

[9] 徐达, 夏祥, 李华, 等. 基于组合函数的弹药装填机器人轨迹规划[J]. 装甲兵工程学院学报, 2013,27(2): 43-46.

[10] 徐达, 夏祥, 李华, 等. 基于图解法与蒙特卡洛法的弹药装填机器人工作空间分析[J]. 火炮发射与控制学报, 2014, 35(2): 16-19.

(责任编辑:尚彩娟)

Dynamics Analysis and Simulation of Ammunition Loading Robotic Arm Based on Virtual Prototype

LUO Jian-hua, XU Da

(Department of Arms Engineering, Academy of Armored Force Engineering, Beijing 100072, China)

The statics of ammunition loading robotic arm is solved in detail on the basis of the virtual prototype of new ammunition loading robotic arm, and the mathematical expression is got. The dynamic model of ammunition loading robotic arm is built by using the Lagrange energy balance method, and the dynamic simulation analysis is realized based on ADAMS. The curve charts of the joint’s angle, force and torque are got, which lays the foundation for real-time control of ammunition loading robotic arm, and also provides the basis for structure design optimization.

ammunition loading robotic arm; dynamics analysis; virtual prototype

1672-1497(2015)03-0071-04

2015-03-06

罗建华(1967-)，男，教授，博士。

TJ203+.3; TP391.9

A

10.3969/j.issn.1672-1497.2015.03.014