基于年检数据的维修器材储存期限预测模型

李志伟， 高 崎， 刘慎洋, 高铁路， 雷 敉

(1. 军械工程学院装备指挥与管理系， 河北 石家庄 050003； 2. 93544部队， 河北 保定 072600)

基于年检数据的维修器材储存期限预测模型

李志伟1, 2， 高 崎1， 刘慎洋1, 高铁路1， 雷 敉1

(1. 军械工程学院装备指挥与管理系， 河北 石家庄 050003； 2. 93544部队， 河北 保定 072600)

利用后方仓库中维修器材技术检查产生的年检数据来估计维修器材的储存期限，分析了年检数据的特点，并将其转化为区间数据；对比分析了3种区间数据处理模型的特点，利用最大似然法建立了基于区间数据的维修器材储存期限回归方程；通过期望最大化(Expectation Maximization, EM)算法给出了回归系数和随机误差的迭代求解式，最后通过模拟实验验证了该方法的稳定性和可行性，为系统解决基于年检数据的维修器材储存期限估计问题提供了一种可行方法。

维修器材；储存期限；年检数据；预测模型

准确预测器材储存期限是实现器材精确化保障的基础，也是合理安排器材轮换周转的先决条件[1-2]。当前，除了油料等在包装上注明保质期外，相当一部分器材只给出了储存期限的保守估计值，甚至一些器材至今都没有储存期限的相关规定，因此储存期限的研究既重要又紧迫。现有维修器材储存期限预测方法主要有2类：1)储存可靠性实验方法[3-4]，该类方法虽然严密，但费用较高；2)基于基层级器材仓库或使用分队数据的预测方法[5]，该类方法虽然费用很小，但数据质量难以保证，错漏情况较多。

仓库年度技术检查数据(简称“年检数据”)产生于正常业务工作，数据收集成本低，数据量相对较大，但维修器材具体失效时间未知。本文针对年检数据特点，建立了一种维修器材储存期限预测模型。该模型较好地规避了具体失效时间未知的问题，并用期望最大化(Expectation Maximization，EM)算法成功求解模型参数，与传统Newton-Raphson算法相比，当应力因子较少时，2种算法均能收敛到要求的精度，但EM算法所需的迭代次数更少。最后通过模拟实验验证了该模型的有效性。

1 年检数据分析与处理

年检数据是通过在后方仓库对储存的维修器材进行技术检查而获得。对某种维修器材实施检测时，要求从不同批次、不同储存年份的库存中抽取一定比例的维修器材进行检测，检测结果如表1所示(实际数据包含多个批次、多组参数测量值)。

表1 某5 Ω电阻的年检数据

设表1中共有k组年检数据，第j年度共检测mj个批次，其中：第l批次的储存时间为tjl，样本量为njl，失效数为fjl，检测年份为Tj，出厂年份为Tp，储存时间为Y,则Y=Tj-Tp。

区间数据处理方法主要有以下3种。

1) 故障内插法[2]。该方法假设时间区间内的多次故障按照相等的时间间隔依次发生，可将区间数据转化为普通的寿命数据，然后进行分布拟合，并检验所选择的分布类型的拟合度是否良好，再进行参数估计，最终得到储存期限估计值。该方法的优点是可简化求解过程，得到一个粗略的估计值; 其不足是故障次数等间距的假设缺乏依据，误差较大。

2) 残存比率法[2，6]。该方法是处理非参数随机截尾区间数据的典型方法。其采用迭代的思想定义维修器材在时刻t(i)的储存可靠度，当前时刻的储存可靠度R(t(i))=R(t(i-1))S(t(i))，其中:S(t(i))为维修器材在时间区间(t(i-1),t(i)]内的残存概率，其含义为在t(i-1)时刻储存状况良好的维修器材继续储存至t(i)时刻依然完好的概率。与故障内插法相比,该方法没有过于苛刻的假设，但库存的维修器材处于动态的收发平衡中，以军区某维修器材仓库为例，平面库房的收发作业年均上百次，造成丢失(删去)观测的维修器材数量较多，测算误差难以控制。

3) 回归方法。维修器材的储存期限是多个因素共同作用的结果，与温度、湿度、微生物、太阳辐射、老炼频率等多种因素相关。回归方法能揭示各个影响因素对储存期限的作用关系。从揭示储存失效规律的深刻程度以及预测准确程度的角度来看，回归模型最适合用来测算器材储存期限。然而，经典回归模型[7-9]要求因变量和自变量的观测值均是一个确定值，而年检数据汇总后得到的是区间数据，因此需要对回归模型进行改进，建立基于区间数据的回归模型。另外，基于区间数据的回归模型应用常规的最大似然估计法确定回归系数时，无显式解，如何寻找合适的求解算法是另一个关键问题。

传统的求解方法是采用Newton-Raphson迭代方法，但该方法需要进行2次微商计算，计算繁琐，且易出错。EM算法是一种求后验分布众数的算法，避免了Newton-Raphson算法繁杂的微商运算。为了优化模型求解，本文应用EM算法[10]来求解模型。又由于年检数据量有限，采用Bayes方法融合先验信息可进一步提高测算精度。

基于以上分析，本文利用基于区间数据的回归模型来描述维修器材储存失效的影响因素与储存期限之间的因果关系，并利用基于Bayes方法的EM算法迭代求解模型。

2 模型的建立

根据年检数据的特点，失效数据分别落入r个(t(i-1),t(i)]区间，1≤i≤r，区间中的失效数为fi。区间数据回归模型为

(1)

式中：εih:i.i.dN(0,σ2),i=1,2,…,r,h=1,2,…,ni。 似然函数为

(2)

根据区间数据随机误差独立同分布假设可知

又由于区间数据汇总了不同年份、不同批次的样本数据，样本量较大，依据大数定律可知随机变量和近似服从正态分布，即

(3)

代入似然函数,整理后可得

对似然函数取对数可得

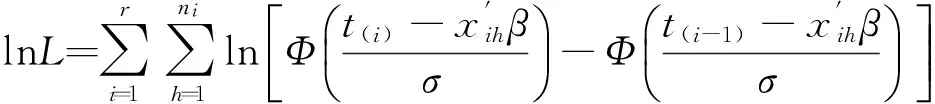
(4)

将对数似然函数分别对β和σ2求导，并令其为0，得到储存期限回归系数及随机误差求解方程组：

(5)

3 模型求解算法

EM算法是一种针对具有状态隐含性的参数估计算法，由于区间数据是一种信息损失型数据，因此该算法非常适合求解当维修器材储存失效具体时间缺失时，储存期限预测模型的参数估计问题，得到维修器材的储存期限预测回归方程。

EM算法是根据年度检测数据汇总后的区间数据来估计未知参数的一种迭代算法，可用来计算后验观测分布的众数。其原理是：根据不断更新的区间数据，在E步通过求条件期望消除潜在数据的影响，在M步求参数的最大似然估计值，更新原参数估计值，且在迭代的过程中参数估计值将逐渐收敛。具体步骤如下。

设Yo为观测数据，Ym为潜在数据，f(θ|Yo)为θ的后验观测分布，f(θ|Yo,Ym)为加入Ym后的添加后验分布，f(Ym|θ,Yo)为在条件θ和Yo下潜在数据Ym的分布密度函数，θ(l)为第l+1次迭代开始时的估计值。

1) E步：求Ym的条件期望

Q(θ|θ(l),Yo)=E[logf(θ|Yo,Ym)|θ(l),Yo]=

∫[logf(θ|Yo,Ym)]f(Ym|θ(l),Yo)dYm。

(6)

2) M步：求Q(θ|θ(l),Yo)的最大值，得到θ的更新值θ(l+1)，并使

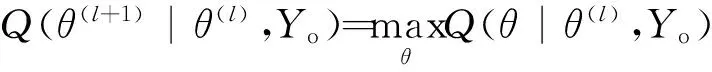
(7)

对于储存期限的求解，由于落入区间(t(i-1),t(i)]的失效数为fi，相当于EM算法中的观测数据Yo，这些失效维修器材的真实寿命Y=(y1,…,yfi)为潜在数据Ym。

由式(6)、(7)可得区间数据回归系数的EM算法求解迭代公式为

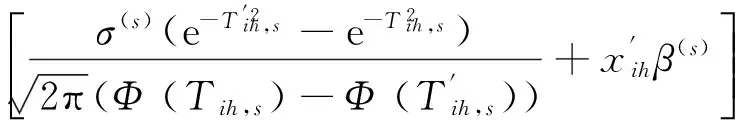
(8)

(σ(s+1))2=

(9)

4 模型验证

由于依据实际年检数据得出的储存期限没有对应的实际值进行比较，因此首先通过仿真方法获得模拟数据，然后利用模拟数据计算模型的预测偏差，验证算法的有效性。

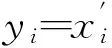
取β=(12,15)，σ=1，t(i)=i,i=0,1,2,…，为储存的年数，n=1 000。当初值β0=(5,10)，σ0=0.5时，回归系数、方差的预测值和偏差如表2所示。

表2 回归系数、方差的预测值和偏差

由表2可以看出:经过反复迭代后，该算法均能以规定的精度收敛到预测模型回归系数和方差的真实值，表明该算法具有较高的稳定性和有效性。Newton-Raphson算法与EM算法的迭代次数对比如图1所示。

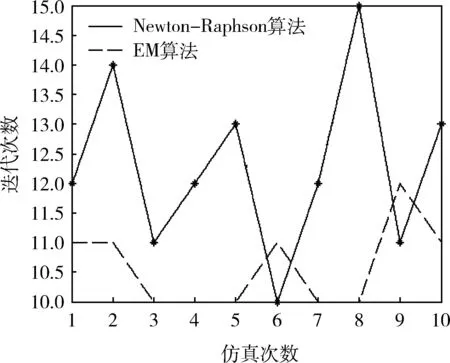
图1 Newton-Raphson算法与EM算法的迭代次数对比

由图1可知：按照本文设定的模拟实验方案进行参数估计，EM算法比Newton-Raphson算法所需的迭代次数少。更重要的是EM算法简单、易操作，当应力因子数量多时，其优势将更加明显。

[1] 高崎.军械维修器材管理学[M].北京：国防工业出版社,2012：115-152.

[2] 郭芳筠，王德润，李海昌,等.军械装备贮存可靠性工程[M].北京:解放军出版社,1999：199-316.

[3] 单永海，张军，王全正，等．机枪身管常温综合寿命实验技术研究[J]．兵工学报，2013，34(1)：1-7.

[4] 刘虎.恒定应力加速寿命实验成组实验数据的Bayes统计分析[J].电子产品可靠性环境实验,1993(2):87-93.

[5] 曹辉，万民侃，陈咏梅.火炮贮存可靠性研究[J].军用标准化,2004(4):46-48.

[6] 张永进，赵明.基于定期检测的贮存可靠性模型及其参数估计[J]. 系统工程理论与实践,2008(10):82-88.

[7] 李鑫，曹显兵.不完全数据下回归模型的参数估计[J]. 数学的实践与认识,2013,43(16):191-196.

[8] Nakagawa T. Optimal Inspection Policies for a Storage System with Degradation at Periodic Tests[J]. Mathematical and Computer Modeling,2000,31(10): 191-195.

[9] 军械工程学院贮存可靠性课题组.地面贮存环境条件分类及贮存环境因子确定方法[R]. 石家庄：军械工程学院, 1994.

[10] 司小胜，胡昌华，李娟.Bayesian更新与EM算法协作下退化数据驱动的剩余寿命估计方法[J]. 模式识别与人工智能，2013,26(4)：357-365.

(责任编辑: 王生凤)

Forecasting Model of Equipment Storage Life Based on Annual Technical Inspection Data

LI Zhi-wei1,2, GAO Qi1, LIU Shen-yang1, GAO Tie-lu1, LEI Mi1

(1. Department of Equipment Command and Administration, Ordnance Engineering College, Shijiazhuang 050003, China；2. Troop No. 93544 of PLA, Baoding 072600, China)

The annual inspection data generated from the technical inspection for maintenance equipment in base warehouse is used to predict the storage life of equipment, the characteristic of annual inspection data is analyzed, and then the inspection data is transformed into grouped data. Characteristics of three kinds of models for processing grouped data are compared and the storage life regression equation for grouped data is built by maximum likelihood method. The regression coefficient and iterative solution with random error are provided by Expectation Maximization (EM) algorithm. Finally, The method is proved to be stable and feasible through simulation, which offers a workable method for the estimation of equipment storage life based on annual inspection data.

maintenance equipment; storage life; annual technical inspection data; forecasting model

1672-1497(2015)03-0014-04

2015-01-21

李志伟(1986-)，男，硕士研究生。

E92

A

10.3969/j.issn.1672-1497.2015.03.004