基于利益博弈的整车物流企业联盟收益分配
杜志平,王 朋
(北京物资学院,北京 101149)
1 引言
随着人们生活水平的不断提高,汽车的需求量越来越大。在巨大的市场需求拉动下,2013 年我国汽车产销双双超过了2000万辆,分别为2211.68万辆和2198.41万辆,并再次刷新全球纪录,连续五年蝉联全球第一。我国汽车业的迅猛发展,对汽车整车物流业的发展提出了更高的要求。整车物流联盟,作为一种有效的物流协作组织形式,在汽车整车运输过程中,其重要作用日益凸显。如何公平合理地对物流联盟进行收益分配,是整车物流企业联盟必须要解决的重要问题。
近年来,许多专家学者对联盟收益问题进行了研究。刘淑婷(2014)[1]通过比较常用的收益分配方法模型,提出各种方法的优缺点,并在此基础上提出了解决虚拟物流企业联盟收益分配的满意度函数模型,综合应用博弈论、概率论、决策理论解决收益分配问题。范海洲,唐德善(2009)[2]利用夏普利值法对物流企业联盟收益分配问题进行了应用仿真。指出在向市场提供同质产品与服务的合作联盟中,当其他影响因子能在成员中均分或可以忽略不计时,利用夏普利值法进行收益分配较为合理、高效;当一些影响因子不可忽略时,对夏普利值法进行一些修正,分配结果也会比较合理。闫黎等(2010)[3]针对多个中小物流企业,综合考虑成员企业的机会收益、贡献及主导企业的影响,利用合作对策理论,探讨联盟的收益分配,构建收益分配模型,并用风险共担思想对分配结果进行修正。李彤,张强(2010)[4]以企业联盟不满意度为出发点,借助合作对策中以超出值来表示企业不满意度的概念,在合作对策的解集Selectope 中筛选出有助于公平原则的解,提出了一种糅合了联盟稳定性的企业联盟收益分配方案。万经花(2013)[5]采用抽象规则即无规则类虚拟变量的改进方法,对物流联盟的收益进行量化分配实证,并通过仿真将改进前后的Shapley 法加以比较分析,实现了对物流联盟收益分配机制理论到实践操作的流程呈现,并为进一步完善物流联盟的利润分配提供了理论与实践的又一实证论据。郭鹏,陈玲丽(2014)[6]在合理地度量与评价盟员在联盟中的贡献,考虑联盟公平的制定及联盟参与程度的前提下,引入合作博弈和模糊理论来研究模糊联盟收益分配问题。在模糊博弈环境下,引入模糊变量的可信性测度,建立了模糊联盟收益分配的模糊期望值规划模型。丁斌等(2012)[7]运用收益分配模型与博弈论的相关方法,设计了基于旁支付的激励机制模型。指出在旁支付激励机制下,成员企业的努力水平与虚拟企业期望总收益均得到了一定的提升;应用博弈论的分配理论与Nash 讨价还价方法设计了利润分配模型,在满足个体理性与集体理性的条件下,将合作博弈产生的合作剩余进行了分配,提出了一个可行的分配方案。
已有的联盟收益分配文献主要研究了几种比较经典的联盟收益分配方式,并且研究的重点多是针对非合作动态博弈问题,而对整车物流企业联盟的收益分配研究较少,本文结合整车物流的特点,根据委托-代理理论和联盟的不同运行阶段,构建了整车物流企业联盟收益分配问题的博弈模型。
2 问题描述
2.1 单一整车物流企业与整车物流企业联盟
整车物流企业联盟是指两个及两个以上的整车物流企业,为了实现资源整合,降低物流成本,提高竞争力等而组成的一个协作性组织,在这个组织中,不同的整车物流企业实现物流网络节点、运输车辆等物流基础设施,甚至是物流任务、信息等资源的共享,以此来提高物流企业的车辆利用率,减少空载,降低物流费用,最终增加整个联盟的收益[8]。
整车物流,简单的说就是指车辆从下线后一直到最终客户手中所进行的物流活动。它是指基于时间竞争的敏捷汽车供应链环境中,以整车作为物流服务标的物,按照客户订单对交货期、交货地点、品质保证等的要求进行快速响应和准时配送。单一的整车物流企业,都是通过自己的物流网络节点及物流设施来提供物流服务,但是随着市场竞争日益激烈及先进技术的应用,企业实现经济扩张的追求明显受阻,很多整车物流企业已经开始尝试通过联盟来追求利润的增长。
由图1和图2可以看出,整车物流联盟的订单处理流程因为有了联盟信息中心的存在,订单和承运车辆可以自行匹配,要比单一物流企业的订单流程更为高效、准确。
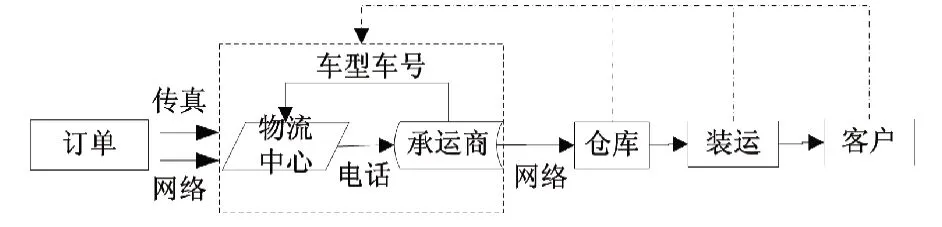
图1 单一整车物流企业订单流程
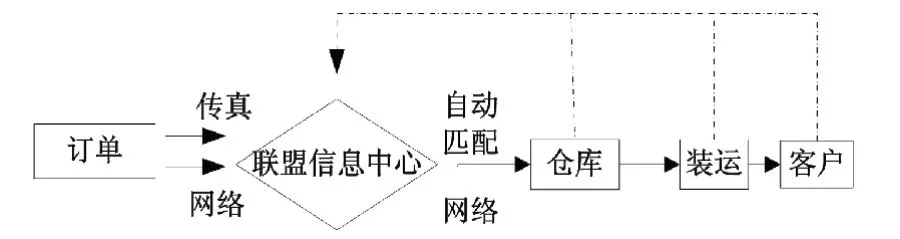
图2 整车物流联盟订单流程
图3表示单一整车物流企业的下游网络节点,图4表示一个整车物流企业联盟的下游网络节点,在该联盟中,A表示物流企业的中转站或中转仓,B表示物流企业的终端营业网点或最终客户,C表示不同企业之间共享的网点。由图3、图4对比可以看出,共享网点的存在,使各个联盟成员的业务范围扩大了,各联盟企业可以共用彼此的运输网络、运输车辆等,从而节省自身的运力。同时,随着各种能够进行优势互补的物流任务的增加,联盟决策者可以整合整个联盟的物流资源及物流任务,这样就实现了全联盟的运力优化,更有利于联盟成员的收益及整个联盟的长远发展。因此,本文所研究的整车物流联盟问题,主要是指整车物流企业间的网络联盟,即信息网络和运输网络。
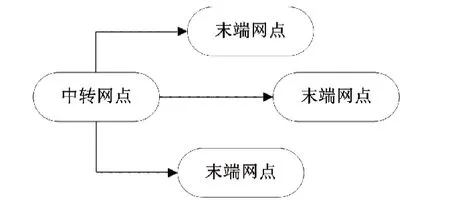
图3 单一整车物流下游网络节点
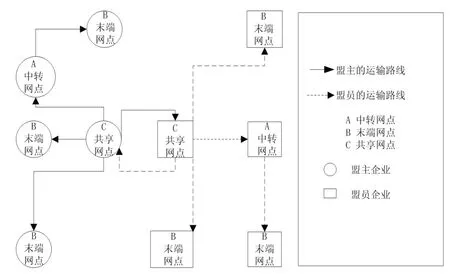
图4 整车物流联盟下游网络节点
在这个联盟中,所有成员企业在进行物流作业时,共享信息处理系统、运输车辆、仓储中心甚至是客户。这样在联盟企业有订单到达时,就自动录入公共的信息处理系统进行统一处理,然后根据订单处理的情况进行车辆的调度或是下级分销中心的交接安排。当订单过小时,共享的信息处理系统可以进行订单的合并,以增加运输车辆的满载率;当订单过大时,可能单个物流企业无法独立完成,这样就可以把订单适当拆分,既能减轻单个物流企业的订单压力,又能帮助该企业进行业务扩展;事实上,很多订单都是单程的,当接到单程订单时,可以通过共享信息系统进行智能配货,安排回程订单,减少运力浪费。
2.2 联盟收益分配模式
整车物流企业联盟构建完成之后,如何公平合理地进行联盟内部的利益分配,是该联盟能够稳定存在和发展的前提,只有在充分保证这一前提下,才能全面激发联盟企业的积极性和创造性。根据对委托-代理理论和联盟收益的研究发现,目前物流企业联盟的收益分配主要有以下几种方式:定额支付式,这种支付模式是根据联盟内部成员事前协商好的任务分配及相应任务酬金,来进行支付的模式。在这种分配模式中,盟主企业享有联盟合作总利润的全部剩余,同时也承担了该联盟运营中的全部风险;按劳分配式,又称产出分享模式,这是一种典型风险共担、利益共享模式。在这种分配模式下,所有参与联盟运营的物流企业,按照一定的比例从总收益中得到自己的部分;复合模式,简单的说就是以上两种模式的混合,各联盟企业既能从联盟总收益中得到一定的固定收益,同时也从总收益剩余中按照一定的比例来获取收益。具体选用哪种收益分配方式,要根据各联盟企业的实力、意愿、风险分担能力、市场实际情况等因素来决定。在现实中,复合模式应用比较广泛,其实,另外两种模式也能看成是复合模式的特例,因此,本文主要研究的是比较常见的一般意义上的复合模式。
3 整车物流联盟相关理论分析
3.1 整车物流联盟成本及收益构成
根据整车物流的成本构成,结合物流功能要素,主要把整车物流的相关成本分成以下几个部分:运输费,主要包括车辆租赁费、过路过桥费等;物业管理费,包括水电网气费、办公费等;仓储包装费,包括仓库及设备租金、产品的包装材料费等;信息费用,包括电话、短信、车载终端费等;维护费,包括各种设施设备折旧维修费、耗材费、人工费、保险费、税金等。可以看成是包括各种人工费用、运输费用、材料费用、信息费等在内的营运成本,以及包括售后服务费用、管理费用、仓库、车辆等在内的非营运成本,或者称之为可变成本与固定成本,相关成本要素也构成了其收益要素。本文假定每一个参与联盟的企业,只参与着一个联盟,即所有的物流资源仅限于投入到这一个物流联盟中。
3.2 整车物流联盟的超额利润分析
假设现有两个整车物流企业I、II,两企业的固定成本分别为为t1和t2。其价格曲线用p=a-cq 来表示,其中,a 是常数,c 代表单位可变成本,p 代表产品价格,q 代表需求量,两企业需求量分别用q1、q2表示,利润用m1、m2表示。双方在同一市场本是竞争关系,但是为了获取更多的利润,双方也会考虑以联盟的形式进行合作,下面以一个简单的模型来探究整车物流联盟中是否存在超额利润[9]。
当两企业分别独立经营时,其收益情况如下:
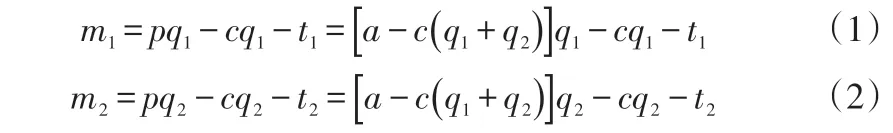
利润最大化需满足的条件如下:

将通过式(3)得出的结果分别代入式(1)、式(2),可得两企业各自利润为:
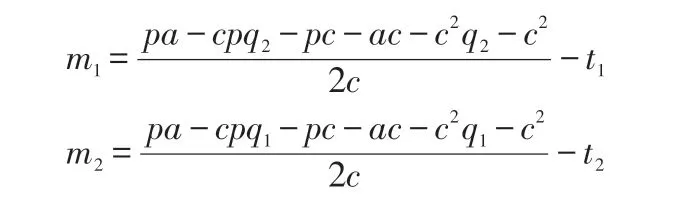
两企业实施战略联盟之后,总利润为:
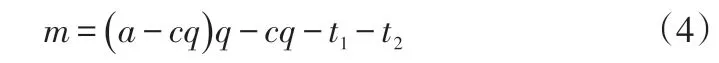
需满足的利润最大化条件如下:
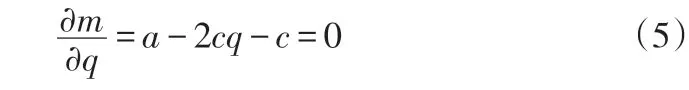
将由式(5)得出的结果带入式(4)可得:
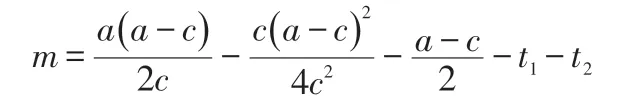
将两家整车物流企业独立经营与采取战略联盟的形式两种情况下所得利润进行比较,可看出整车物流联盟能带来超额利润:
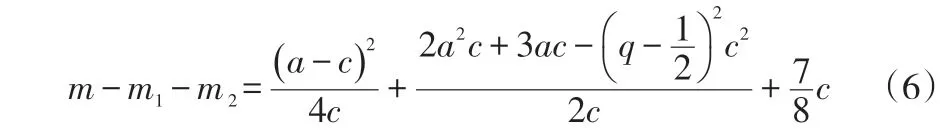
4 模型构建
4.1 收益分配模型
设n个整车物流企业共同组建整车物流联盟A,N={1,2,...,n}为各联盟成员组成的集合,Qi表示成员企业i独立经营时的收益,Li为成员i 采用物流联盟时的收益,总利润为M,Di表示第i个成员企业在物流联盟运营中的投资额,则整车物流企业联盟得以实施的充分条件为:
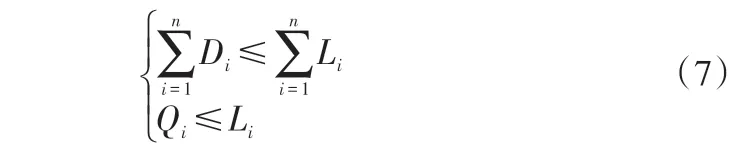
在模型构建时,首先要确保各联盟成员能够收回各自的投资成本,然后在此基础上,根据各成员企业承担的风险、在运营过程中的投资额度、各企业实际运营的工作成效以及企业自身的综合实力等多个方面,对联盟的收益进行分配。
首先把整车物流企业联盟的可分配收益按如下几个要素进行划分[10]:按照成员企业的投资成本进行分配,分配额记为αM ,按照成员企业承担风险的大小进行分配,分配额记为βM ,按照成员企业的额外贡献补偿进行分配,分配额记为χM ,按照成员企业的实际运作成效进行分配,分配额记为δM ,按照成员企业的综合实力水平进行分配,分配额记为εM。
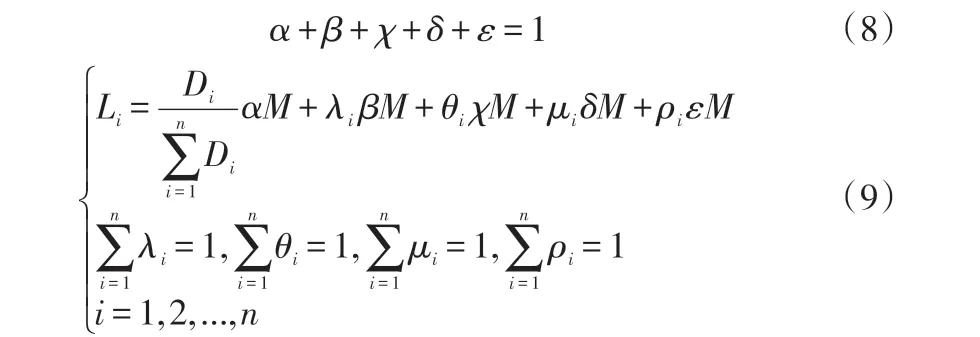
其中,λi表示盟员企业i承担的风险因子;θi表示盟员企业i对该联盟的额外贡献补偿系数;μi表示盟员企业i工作的成效系数;ρi表示盟员企业i的综合能力系数。
4.2 相关系数确定
本文所提到的联盟企业实力都相对均衡,不存在或是很少存在十分强势的企业,在组成联盟之前,需对联盟各成员有很好地了解,并在此基础上促使联盟各成员就收益分配相关问题达成初步协议,并以此作为该联盟将来收益分配的基础。
首先应确定式(9)中α、β、χ、δ、ε 等权重系数,目的是为了能够有效激发盟员企业的积极性,使企业的收入与付出成一定比例,同时,这些系数也是收益合理分配的关键。这些权重系数有多种确定方法,既可通过各联盟企业的协商确定,也可以在考虑如企业实力、投入、人才情况等综合因素下进行确定,确定的结果可以以协议的形式存在,然后根据运营中的实际情况进行相应调整。
确定成员企业i承担的风险因子λi。收益与风险是共存的,高额的收益往往伴随着较高的风险。整车物流企业在联盟实际运作中,会根据各自的专长进行相应的分工,分工不同,则风险各异,为了让收益分配更加合理化,在制定分配原则的过程中,应充分考虑到对于承担高风险的企业进行一定的补偿。
假设盟员企业i承担风险损失的比例是其全额投资,其风险损失率为ai,风险事件发生率为pi,其承担的风险损失为aiDi,则相应风险为ϕi=piaiDi,由此可得,盟员企业i 在风险中承担的风险因子为[11]:
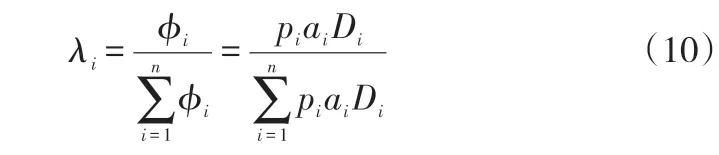
综合能力系数ρi。综合实力涉及到人财物等资源质量、市场地位、品牌优势、市场开拓能力、核心竞争能力、战略管理能力等多个方面。若是成员企业具有较强的综合实力,能为联盟提供较大的贡献,在制定收益分配策略时,则应适当倾斜。对成员企业综合实力的评判还没有统一的标准,本文选取了以下六个方面的指标:资源质量、品牌优势、市场开拓能力、市场地位、核心竞争能力、战略管理能力,用S={S1,S2,S3,S4,S5,S6} 表示,在此基础上构造判断矩阵A,计算出A的最大特征值λmax和特征向量XA,则XA就表示了各指标对于总目标的权重向量[12]。
XA确定了之后,再来确定各盟员企业的指标评价结果。采用如下方式:请专家分别对每个盟员企业各指标进行打分,采用10分制,最后结果为所有专家打分的平均值,各盟员企业六项指标的平均分构成一个矩阵K,则综合能力系数可表示为ρ:

对ρ 进行归一化处理,得出ρi,即是综合能力系数值。
盟员企业i 对联盟所做额外贡献的补偿调节系数θi。由于环境的不确定性,整车物流联盟在实际运营中往往会面临一些突发问题:客户要求较高的技术标准,或是要求时间弹性较低,或是市场需求量增长过快等,此时整个联盟就需要对运行要求及运行策略进行相应的调整,可能会出现某些成员企业承担的任务减少或是增多的情况,这时对任务量减少的企业的收益分配也应适当减少,反之,对于做出额外贡献的成员,其运营成本可能会增加,就要适当增加其收益分配对其进行补偿。补偿额外运营成本时,引入补偿调节系数θi,θi∈[0 ,1] ,其具体值由联盟企业视情况商定。
工作成效系数μi的确定。主要用完成任务数及任务的技术含量来衡量某成员的工作成效,其中,技术价值用任务的难度系数ω 来表示。设整个联盟的任务可以看成由j(j=1,2,...,m)种不同类型子任务组成,各类型子任务对应的难度系数为ωj,ωj∈( 0,1] ,bij为企业i 分配到的j 型子任务的个数,本文认为利润与贡献成正比,由此可得盟员企业i 工作成效系数μi为:
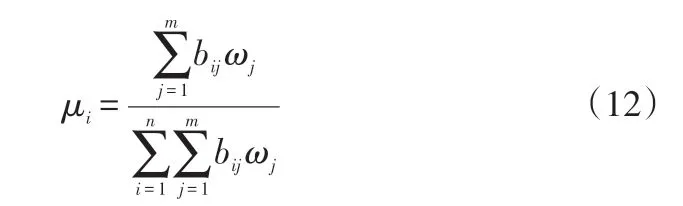
4.3 算例分析
假设某整车物流企业战略联盟A 由甲、乙、丙3 个盟员企业组成,并且他们之间的联盟是完全的,即各盟员企业只参与了联盟A,没有参与到其他联盟中去,设成员企业i(i=1,2,3)在联盟运作中的收益为Li(单位:万元),M 为总利润,4500 万元,总成本D 为1800 万元。甲、乙、丙的投资额分别为750 万元、600万元、450万元。假定协议中规定的α、β、χ、δ、ε 取值分别为0.1、0.2、0.1、0.4、0.2。则由上述可得出各系数值(为计算方便,最终结果均保留小数点后一位):
(1)风险因子λi。各成员企业风险发生率分别设为0.3、0.2、0.5,风险损失率分别设为0.2、0.3、0.5,由公式ϕi=piaiDi求得各企业所承担的风险为:ϕ1=0.3×0.2×750=45,ϕ2=0.2×0.3×600=36,ϕ3=0.5×0.5×450=112.5。
再由式(10)可得λ1=0.2,λ2=0.2,λ3=0.6。
(2)补偿调节系数θi的确定。假设在联盟运行现状已知的情况下,最终确定各成员企业的补偿调节系数为0.4、0.3、0.3。
(3)工作成效系数μi的确定。设此整车物流联盟中的总任务为100 个,难度系数分为0.5、0.3、0.2 三等。具体见表1。
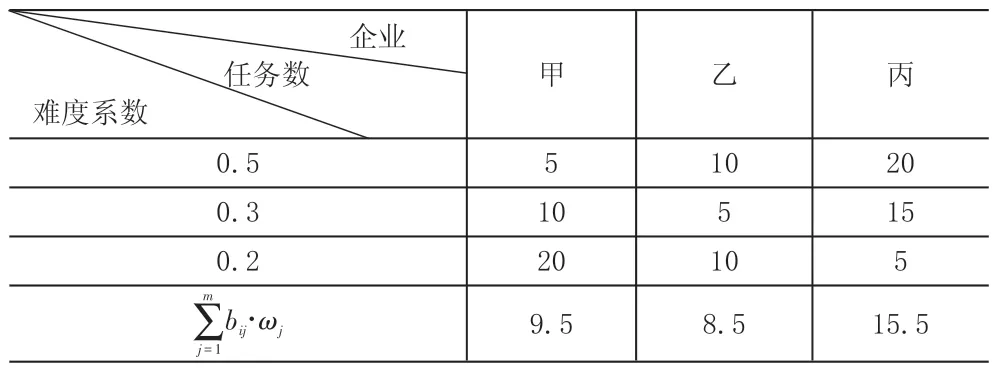
表1 整车物流联盟任务分布情况
由式(12)可得μ1=0.3,μ2=0.2,μ3=0.5。
(4)用层次分析法确定综合能力系数ρi

计算出A的最大特征值λmax=0.31,判断矩阵一致性比例为0.087,其值小于0.1,判断矩阵满足一致性。并求得XA=( 0.23,0.04,0.06,0.37,0.86,0.11) ,通过十位专家的评定打分,求其平均值后,最终得到矩阵K。

由式(11)可得:ρ=XA·KT=( )5.23,5.72,5.91 ,归一化处理得:ρ′=(0.31 ,0.34,0.35 ),即ρ1=0.3,ρ2=0.3,ρ3=0.4。
最后将所得的系数分别代入式(9)中,计算得:

由以上分析可知:在该物流联盟中,企业丙的收益是最高的,但是其投资额却不是最高的。出现这种情况是可以理解的,企业丙的收益除了相应的成本收益之外还有较高的风险收益和工作成效收益,由此可以看出企业丙具有较高的核心技术,综合考虑,其对整个联盟的贡献最大,故获得的收益最高。企业甲的收益主要来自于其较高的工作成效和整车物流任务的风险收益。企业乙的收益主要来源于其工作成效和综合能力水平,但任务数比较少,投资额比较居中,因而其最终的收益相对较少。这种收益分配方案,首先保证了各企业的成本收益,每个企业的收益均超出其投资额较多,同时根据各企业对联盟的贡献进行多元化、灵活性的收益分配,既能保证联盟企业的积极性,也能促进联盟的健康发展。
5 结语
本文根据委托-代理理论建立了整车物流企业联盟收益分配的博弈模型。首先分析了整车物流联盟运行的成本及收益构成,指出在企业联盟的基础上,存在超额利润,为整车物流企业联盟的构建提供了一定的理论依据,并选取了企业投资成本、个体承担风险、个体额外贡献补偿、企业实际运作成效、企业综合实力水平等六要素,作为收益分配的主要着眼点,最后经过算例验证了模型的可行性。整车物流联盟企业的收益分配是多因素综合考虑的结果,本文为整车物流联盟提供了一种可行的收益分配方案,对于不同的整车物流联盟,所需要考虑的利益分配要素可能会有所不同,需要结合实际情况进行分析。
[1]刘淑婷.虚拟物流企业联盟收益分配方法研究[D].重庆:重庆工商大学,2014.
[2]范海洲,唐德善.夏普里值法在物流企业联盟收益分配中的应用[J].中国流通经济,2009,(3):27-29.
[3]闫黎,赵艳萍,罗建强.中小物流企业联盟的收益分配策略研究[J].工业工程,2010,(5):45-47.
[4]李彤,张强.基于不满意度的Selectope解集研究以及在企业联盟收益分配中的应用[J].中国管理科学,2010,(3):112-116.
[5]万经花.基于Shapley 值法的物流联盟收益分配问题研究[J].物流技术,2013,(12):306-308.
[6]郭鹏,陈玲丽.模糊环境下模糊联盟收益分配模型和算法研究[J].模糊系统与数学,2014,(3):103-107.
[7]丁斌,邓志强,曹苏.基于旁支付的虚拟企业收益分配博弈[J].系统工程,2012,(6):24-29.
[8]李亚东,等.动态联盟收益分配问题的博弈研究[J].工业工程,2006,(3):15-18.
[9]Hame G.Competition for competence and interpartner learning with international strategic alliance[J].Strategic Management Journal, 1991,(12):83-103.
[11]Kang Wook Lee,Gibaek Lee,Kang Ju Lee,et al.A dynamic process simulator based upon the cluster-modular approach[J].Korean Journal of Chemical Engineering,1996,13(6):549-553.
[10]赵忠华,王晓华.虚拟企业利益分配要素及其价值确定[J].商业研究,2002,(12):4-5.
[12]李欧阳.第三方物流企业战略联盟收益分配研究[D].长沙:中南大学,2011.

