有限元技术在基于能量平衡的机床动态设计中的应用

□ 徐广晨 □ 翁泽宇 □ 张南南

1.营口理工学院 机电工程系 辽宁营口 115014

2.浙江工业大学 机电工程学院 杭州 310014

1 概述

随着机械制造向着高速和精密加工方向的发展，对机床动态性能的要求也越来越高。在已知工作条件下，为满足机床期望的动态性能，寻找机床最优结构的过程就是机床的动态设计。美国UCA大学的G Bianchi等［1］将机床的动态设计与控制相结合，进行动态优化设计；衣阿华州立大学的J M Vance与ISU研究中心的T P Yeh等［2］应用虚拟现实技术来进行机床结构的形状优化设计；天津大学的张学玲等［3］运用结构动态设计原理和有限元法的变量化分析技术，提出一种数控机床床身结构的动态设计方法和流程；昆明理工大学的尹志宏等［4］讨论了利用优化准则法优化磨床主轴系统机械性能的基本过程，并探讨了优化准则法对机械结构进行优化设计的优越性。

在机床的动力分析和动态设计时，常见的模型有分布质量模型、集中参数模型和有限元模型三种。M Yoshimura和T Hoshi建立了单柱刨铣床分布质量动力学模型；1964年，Malitback和Toylor Tobias提出了用两种简单的单元连接集中质量建立动力学模型方法；1970～1971年间，国际生产工程研究协会CIRP对基于集中质量法建立机床动力学模型方法进行了联合研究。为提高分析和设计精度，用更接近实际结构的模型来进行机床动态研究，一些学者把有限元法引入机床动态特性研究中。1968年，Stephan把有限单元模型应用于机床结构建模中［5］；到了20世纪90年代，随着计算机科学的发展，许多商业的有限元软件不断成熟，在对复杂机械结构动力分析和动态设计方面，有限元法已成为一种应用广泛的建模方法。

基于能量平衡的结构优化方法研究同样也取得了一定的成果，得到了广泛的应用。M Yoshimura、T Hoshi等［6-8］对以发生再生颤振危险最小为目标，对模态柔度和能量平衡为基础的动态优化设计原理和方法进行了详细的介绍；星铁太郎［9］对基于能量平衡法的结构修改方法进行了系统研究，其核心是把结构的振动强度或动柔度限制在一定的范围内；哈尔滨工业大学机床教研室的张宗兰［10］应用能量平衡原理，建立了光学曲线磨床的集中质量模型，对其进行了动态特性的研究,利用数学模型对机床进行了理论分析与计算,指出机床结构中的危险模态及薄弱环节,并对薄弱部件提出优化意见；湖南大学的熊万里等［11］建立了高速精密电主轴单元的集中质量模型，采用模态柔度和能量平衡相结合的原理，找出电主轴单元的薄弱环节，然后在一定条件下，修改这些薄弱环节的结构设计参数，降低模态柔度，提高了优化效率；上海交通大学机电分校的郑伟中［12］利用能量平衡原理，采用集中质量模型对M1432A万能外圆磨床砂轮架进行了能量分布计算，找出整机的薄弱部件，为后面的砂轮架部件的抗振优化设计提供了理论基础。

本文以有限元技术为基础，应用基于能量平衡的结构优化方法，通过能量的分析，进行结构动态特性的评价、修改及优化。

2 能量计算及结构动态特性评价

整个系统在振动过程中的总能量是各子结构能量的总和。设整个结构A的第s个子结构以第r阶模态振动时的最大惯性能为Tsr、最大弹性能为Vsr。由于能量是标量，整个结构A以第r阶模态振动时的最大惯性能T、最大弹性能V，它们分别是所有子结构相应各类能量的总和，即：

子结构各类能量可以分别表示为：

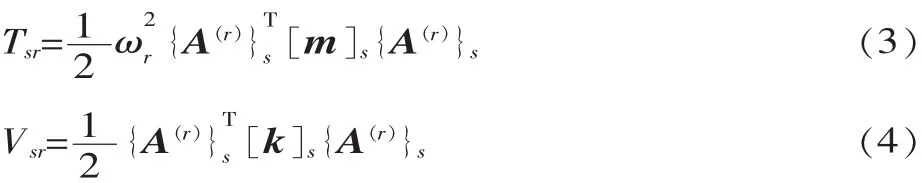
式中：ωr为结构的第 r阶固有频率；｛A（r）｝s为系统以第r模态振动时，第s个子结构的所有节点在各运动坐标方向的振幅列阵；｛A（r）为｛A（r）｝s的转置矩阵；［m］s为 s的惯性矩阵；［k］s为 s的刚度矩阵。

将子结构的各类能量与整个结构的相应能量之比称为子结构s第r阶模态的惯性能分布率和弹性能分布率。能量分布率高的子结构，说明它与其它子结构相比质量过大或刚度过低，是需要进行结构优化的子结构。惯性能分布率高的子结构应着重减小其质量，弹性能分布率高的子结构应着重提高其刚度，使结构的能量分布均匀化，这就是基于能量平衡的机床结构优化理论［13］。

对于机床能量分布均匀程度的估计，可以借助于振动系统各阶次模态的动能和势能分布的均方差来定量描述机床结构各阶次模态的能量分布的均匀性，并判定其偏离最优设计的程度。

机床振动系统各阶次模态的动能和势能的均方差可以表示为：

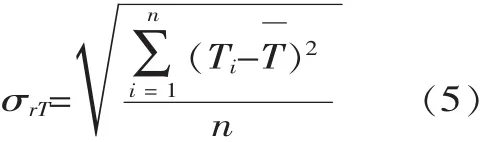
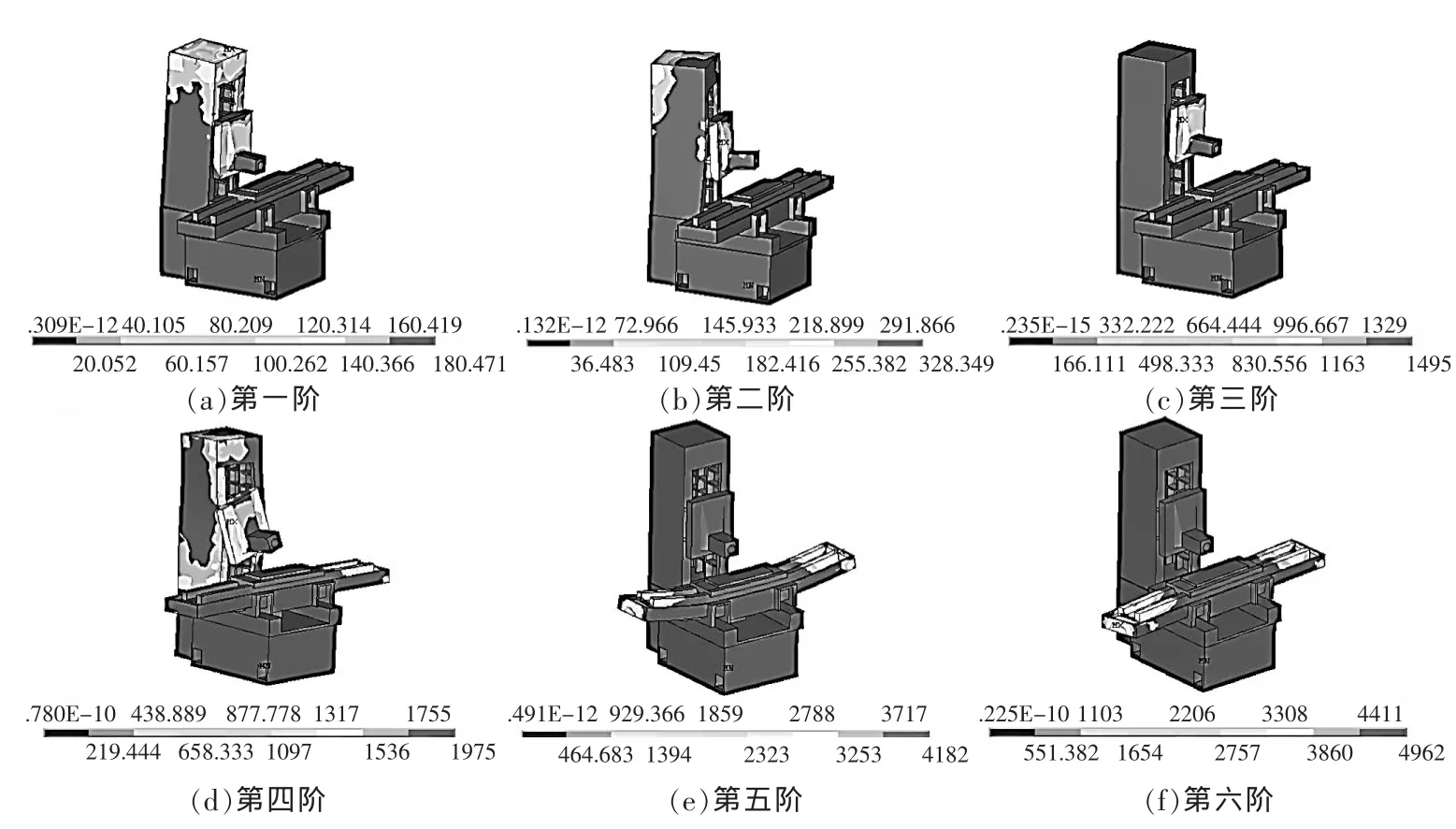
▲图1 磨床前六阶动能分布图

式中：σrT为机床第r阶动能的均方差；Ti为第i个单元的动能值；T为第r阶的动能平均值；σrV为机床第r阶势能的均方差；Vi为第i个单元的势能值；V为第r阶的势能平均值；i为第 i个单元；n 为单元数［14］。

在现有的文献中，国内外学者进行基于能量平衡的结构优化均针对的是结构的集中参数模型。集中参数模型在建模过程中进行参数估算较繁琐，而结构的有限元模型在进行结构动力学建模、结构修改和能量分布率计算的过程中将充分显示其优势［15］。

▲图2 磨床前六阶势能分布图

3 基于能量平衡的机床有限元模型动态分析

将有限元技术应用于基于能量平衡的结构动态特性分析是一种有效和便捷的方法，本文用这种方法来分析某超精密平面磨床的动态特性。

用有限元分析软件ANSYS对床身进行模态分析，得出其前六阶模态的固有频率分别为：50.9 Hz、86.7 Hz、120.5 Hz、154.7 Hz、171.6 Hz 和 232.2 Hz。

磨床前六阶模态的动能分布如图1所示。

由动能分布图可知，能量集中的地方主要有立柱的上下两端、磨头、拖板的两端以及床身的前板面，分析知道，主要是以下几个方面原因造成。

（1）由于立柱纵向刚度小、两端质量大，使立柱两端特别是立柱上端振幅大，出现立柱两端动能集中的情况；

（2）由于磨头本身质量大，或者磨头与立柱的结合面刚度小，造成磨头振幅大，增大了其动能；

（3）由于拖板与床身结合面上方的位置刚度低，拖板两端质量大，使拖板两端振幅变大，其动能也随之变大。

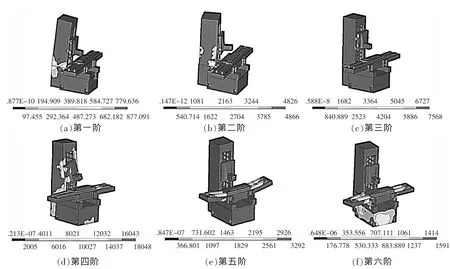
磨床前六阶模态的势能分布如图2所示。

由势能分布图可知，能量集中的地方主要有拖板-床身结合面上方的位置、磨头-立柱结合面以及床身前板面，分析知道，主要是以下几个方面原因造成。

（1）由于拖板两端跨度比较长，引起刚度不足，容易产生较大的变形。

（2）磨头-立柱结合面的结合面刚度偏低，容易造成结合处势能集中；

前六阶模态的动能均方差和势能均方差见表1，由表1分析可知，该磨床能量分布较为分散，均匀度低，离结构的最优设计还有很大的距离。

上述仿真分析结果可以对机床结构优化设计起到指导作用，以减小在结构改进过程中的盲目性。

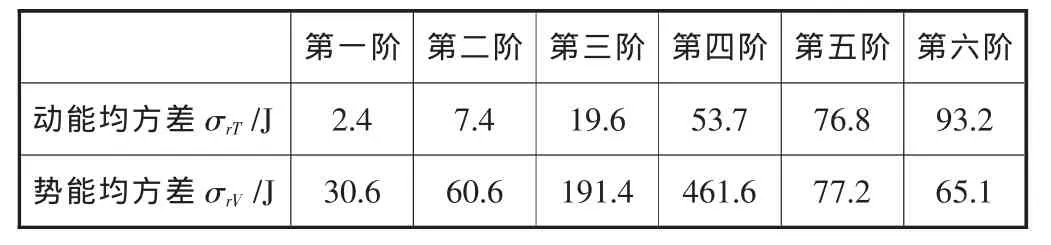
表1 前六阶模态参数

4 结论

将有限元技术应用于机床结构动态特性分析，在进行结构动力学建模、结构修改的过程中，提高了建模的精度，充分显示了其优势。利用基于能量平衡的有限元技术进行动态设计，可以直接分析结构的能量分布情况和振型。对结构进行改进时采用能量平衡为主、振型分析为辅的薄弱环节分析方法，提高了动态设计的效率。

［1］ G Bianchi， F Paolucci， P Vanden Braembussche et al.Towards Virtual Engineering in Machine Tools Design ［J］.CIRP Annals-manufacturing Technology，1996,45（1）：381-384.

［2］ T P Yeh， J M Vance.Applying Virtiual Reality Techniques to Sensitivity-based Structural Shape Desigh ［J］.Journal of Mechanical Design，1998，120：620-627.

［3］ 张学玲，徐燕申，钟伟泓.基于有限元分析的数控机床床身结构动态优化设计方法研究 ［J］. 机械强度，2005，27（3）：353-357.

［4］尹志宏，周新民，廖伯瑜.磨床主轴系统优化设计［C］.2001年西南三省一市自动化及仪器仪表学术会议，昆明，2001.

［5］ 梁祖峰.TH6350加工中心主轴系统试验模态分析 ［D］.昆明：昆明理工大学，2003.

［6］ M Yoshimura，T Hoshi.Computer Approach to Dynamically Option Design of Machine Tool Structure［C］.Proceedings of the 12th International Machine Tool Design and Research Conference，Manchester，1971.

［7］ T Hoshi，M Yoshimura.InitialApplication ofDynamic Structural Analysis to Computer-aided Design of Machine Tool ［C］.Proceedings of the 14th International Machine Tool Design and Research Conference，Manchester，1973.

［8］ M Yoshimura.Analysisand Optimization ofStructural Dynamics of Machine Tool by a Synthesis of Dynamic Rigidity Program System ［C］.Proceedingsofthe 16th International Machine Tool Design and Research Conference，London，1976.

［9］ 星铁太郎著，顾崇衔等译.机械加工颤振的分析与对策［M］.上海:上海科技出版社，1984.

［10］张宗兰.能量平衡法在机床结构动态参数优化中的应用［J］.哈尔滨工业大学学报，1987（4）：37-43.

［11］熊万里，温建立，黄红武.高速精密电主轴单元的动态优化设计［J］.机械设计,2004（Z1）：121-122.

［12］郑伟中.用能量平衡原理分析砂轮架的动态特性［J］.机床，1982（1）：34-37.

［13］ 杨肃，唐恒龄，廖伯瑜.机床动力学Ⅱ［M］.北京：机械工业出版社，1983.

［14］翁泽宇，张南南，蔡勇，等.有限元技术在基于能量平衡的机床动态设计中的应用［J］.机械强度，2011，33（3）：411-417.

［15］蔡勇.基于能量平衡原理的机床动态设计技术研究［D］.杭州：浙江工业大学，2007.