次指数分布下复合Poisson风险过程破产概率的渐近公式
赵丽霞
(山西大学商务学院,山西 太原 030031)
0 引 言
风险模型是精算学研究的一个热门话题,国内外众多学者对风险模型中的破产概率问题进行了探讨,得出了破产概率的显式通解或渐近分布[1-8]。文中考虑了带有常数保险费率、常数利息力的复合Poisson风险模型,在次指数分布下推导出了破产概率的渐近公式。
1 模型描述
给定概率空间(Ω,F,P),假定理赔次数过程{N(t),t≥0}服从强度参数为λ的Possion过程,其中,N(t)为时间间隔[0,t]中的索赔次数;{Yj,j≥1}为独立同分布的理赔额随机变量序列,其中Yj表示第j次理赔额,其分布函数为F,满足进一步假 定{N(t),t≥0}与{Yj,j≥1}相互独立。
记

文中假定H为次指数分布,在此基础上研究风险模型的破产概率问题。
总理赔额过程{X(t),t≥0}定义为
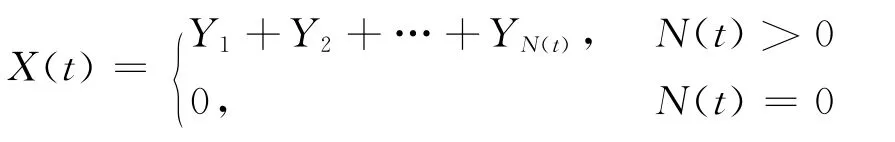
考虑经典风险模型
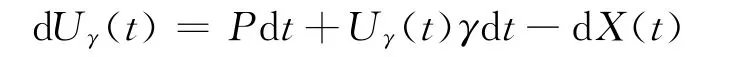
式中:{Uγ(t),t≥0}——保险公司的风险准备金;
P——常数保险费率;
γ——常数利息力。
在以上假定条件下,由文献[1]可知,风险准备金{Uγ(t),t≥0}满足方程
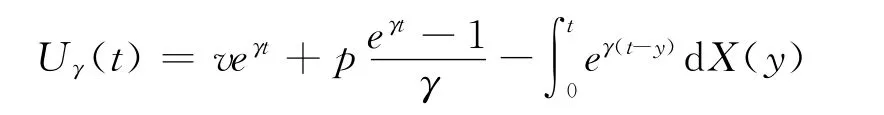
其中v=Uγ(0)≥0为保险公司的初始盈余。定义,称为该盈余过程的终极破产概率。
为研究方便,文中给定以下变量记号:
记ρ=λμ:单位时间内的期望理赔额数量;
φγ(v)=1-Ψγ(v):生存概率;
Gγ(v)=1-Ψγ(v)/Ψγ(0):辅助分布函数;
2 辅助关系
假设安全载负ρ<c成立,由文献[1]可知
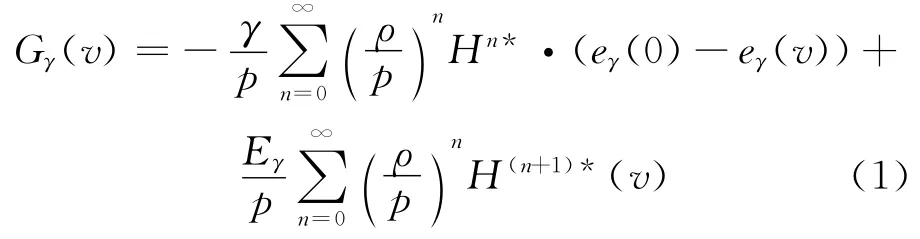
其中,Hn*为Stieltjes卷积,
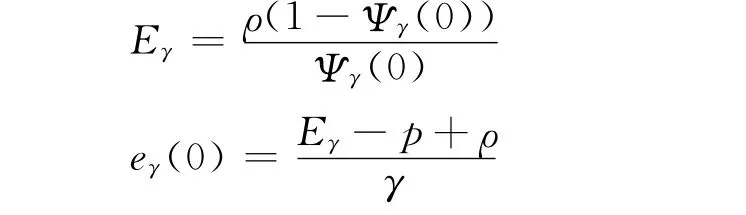
文中将利用Gγ(v)讨论保险公司的破产概率问题。
由Beekman卷积公式,破产概率Ψ0(v)可表示为
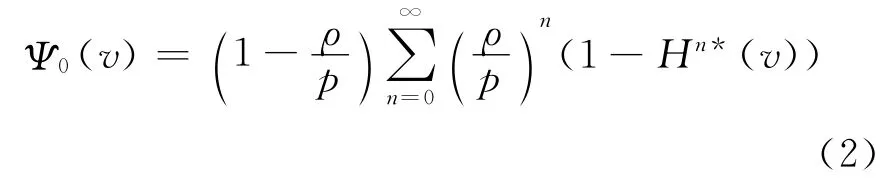
由式(1)和式(2)可得
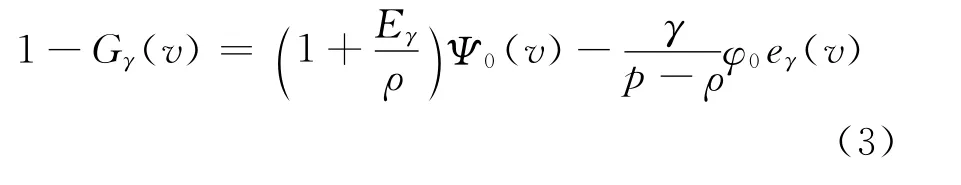
即
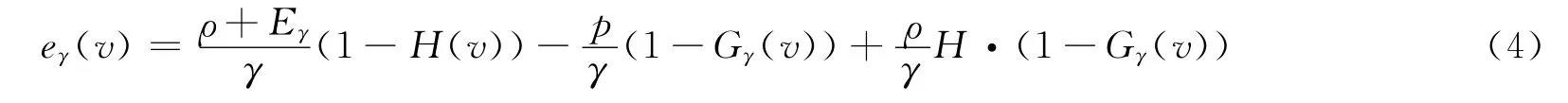
由Laplace-Stieltjes转换,并结合式(2)得
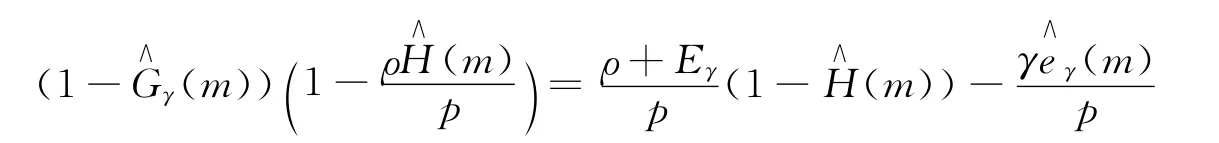
3 主要结论及证明
我们将要在H为次指数分布的假定条件下,通过估计eγ(v)的上、下界进而得到eγ(v)的渐近公式。
定理1 若ρ<p,则
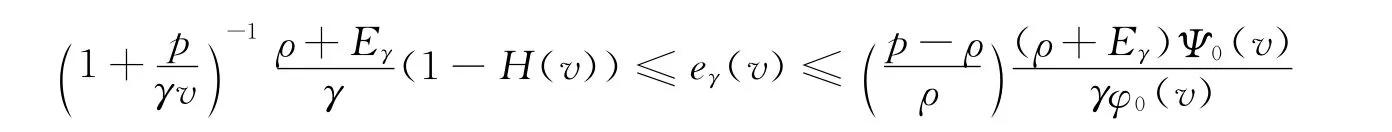
证明:显然eγ(v)≥v(1-Gγ(v)),将其代入式(4),得
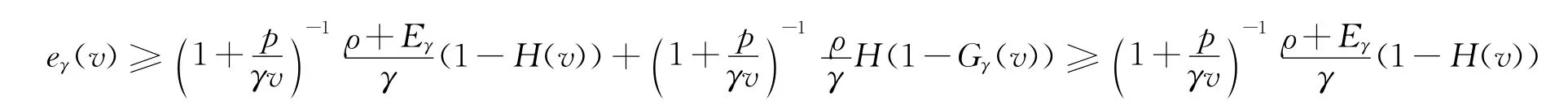
又

得
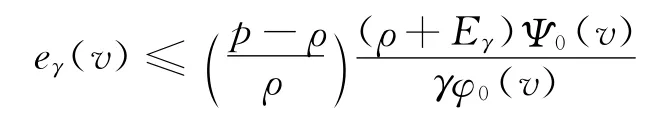
定理2 对于次指数分布H及ρ<p,有
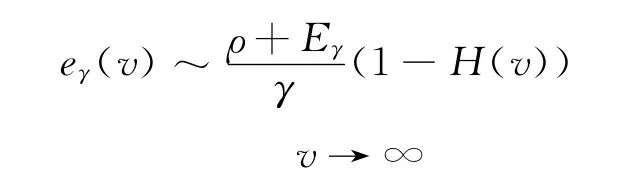
证明:由于
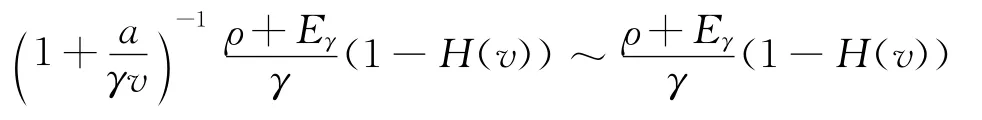
又
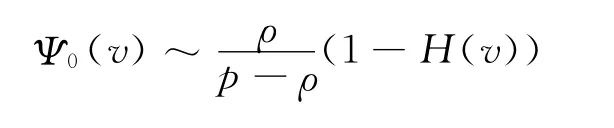
则
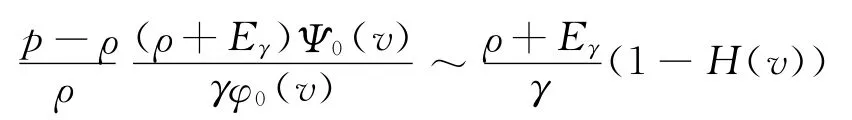
定理3 若H为次指数分布,则

证明:
情形1:ρ<p。
由定理2可知,
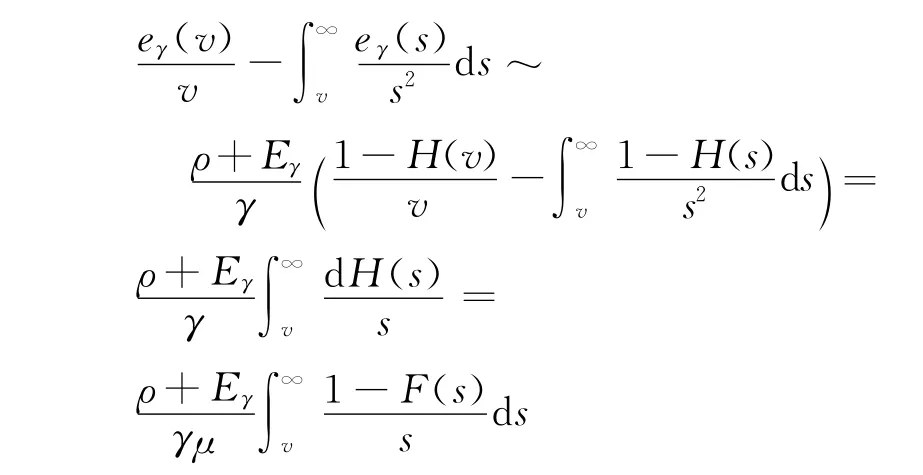
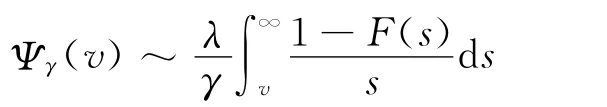
情形2:ρ≥p。
由破产概率的表达式可知,若p≤p′,则Ψγ(v,p)≥Ψγ(v,p′)。若ρ<p′,则由情形1可知,,并且对于任意的且,有
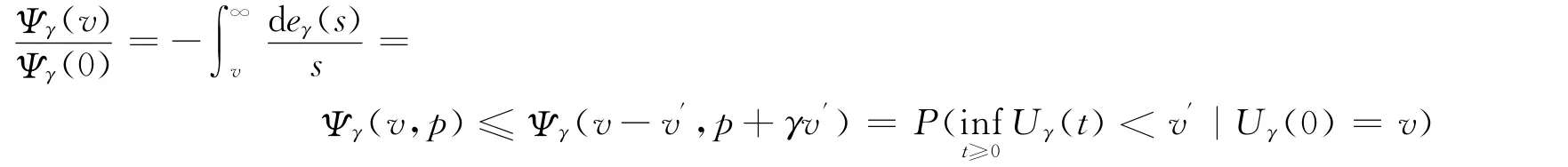
另v′满足ρ<p+γv′,则由情形1可知
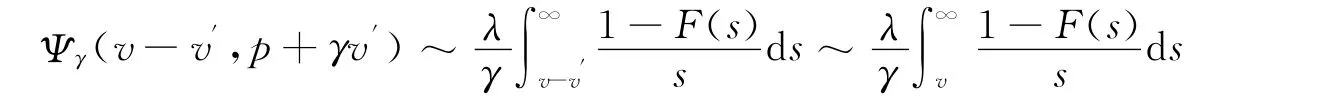
因此,Ψγ(v)上、下界表达式相同,则
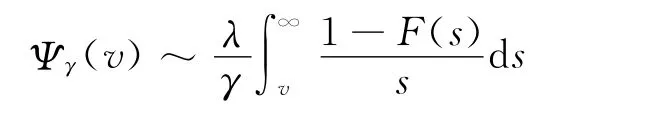
[1] Sundt B,Teugels J L.Ruin estimates under interest force[J].Insurance:Mathematics and Economics,1995(16):7-22.
[2] Asmussen S.Subexponential asymptotics for stochastic processes:extremal behavior,sta-tionary distribution and first passage proba-bilities[J].Annals of Applied Probability,1998(8):354-374.
[3] Kalashnikov V,Konstantinides D.Ruin under interest force and subexponential claims:a simple treatment[J].Insurance:Mathematics and Economics,2000,27:145-149.
[4] Konstantinides D,Tang Q H,Tsitsiashvili G.Estimates for the ruin probability in the cl-assical risk model with constant interest force in the presence of heavy tails[J].Insurance:Mathematics and Economics,2002(31):447-460.
[5] 毛泽春,刘锦萼.索赔次数为复合Poisson-Geometric过程下破产概率的显式表达[J].中国管理科学,2007,15(5):24-28.
[6] 王开永,林金官.带常利率相依风险模型的有限时破产概率[J].东南大学学报:自然科学版,2012,43(6):1243-1248.
[7] 王后春.两险种Erlang(2)风险模型的破产概率[J].工程数学学报,2013,30(5):661-672.
[8] 王开永,林金官.复合相依离散时风险模型的有限时破产概率[J].应用数学,2013,26(4):751-755.
[9] 孙建英.概率统计中的数学建模案例[J].长春工业大学学报:自然科学版,2014,35(2):224-226.

