特征加权优化软子空间聚类算法
庄景晖
(漳州职业技术学院 计算机工程系,福建 漳州 363000)
0 引 言
聚类分析作为一种重要的数据挖掘处理技术,近几年来在生物信息学[1]、文本挖掘[2]和社区发现[3]等许多领域已经得到了广泛的应用。作为一种无监督的分类方法,聚类分析主要目的是根据某些预先定义的标准对数据集进行划分,进而形成多个簇类,划分的结果使得簇内的样本尽可能相似,不同簇间的样本尽可能相异[4]。现今,随着信息技术的飞速发展,数据的采集变得更加方便与迅速,也因此导致了人们获得的数据集变得更大、更复杂。与低维数据相比,在高维数据空间中通常存在着许多并不相关的属性[5],同时还存在着“维度效应”的问题,从而导致多数传统聚类分析方法无法有效地聚类分析高维数据。为了解决这类问题,国内外研究人员针对高维数据的分析提出了很多的聚类方法[6],其中的子空间聚类就是一类代表性的方法。
子空间聚类是指在高维数据空间中挖掘存在于某些低维子空间中簇类的技术[7]。它将数据集划分并形成多个簇类,从中寻找出数据集中各个簇类所对应的子空间。在每一个簇类中,赋予各维度属性不同的权值,权值代表属性对于簇类的相关程度。根据已有的研究成果,子空间聚类方法可被划分为硬子空间聚类和软子空间聚类两大类[2]。硬子空间聚类方法在聚类过程中赋予簇类中各维度属性的权值为0或1,用来表示属性与该簇类不相关或相关。与硬子空间聚类相比,软子空间聚类区别在于在聚类过程中赋予簇类中各维度属性[0,1]区间的权值。与硬子空间聚类相比,软子空间聚类不仅反映了属性与簇是否相关,而且还反映了各相关属性在相关程度上的差异[8],因此,软子空间聚类近年来在数据挖掘领域中是一个重要的研究课题[2,7,9-10]。许多新的软子空间 聚 类 算 法,如EWKM[2]、FWKM[9]、FSC[10]已经被提出并应用到不同领域,它们的聚类性能也越来 越高。然而,这些 软 子 空 间 聚 类 算 法[2,9-10]考虑更多的是对数据集划分的优化[11],并没有考虑对各簇类所在的子空间进行优化,在一定程度上降低了算法效率和聚类精确度。原因在于软子空间聚类中,每一个簇类的成员一般是由算法发现的子空间和加权欧式距离共同确定的。因此,子空间的优化对聚类算法的效果有着重要影响。
文中提出一种新的基于特征加权优化的软子空间聚类算法(Soft-subspace clustering based on feature optimization,SCFO),用于高维数据的聚类分析。SCFO算法优点在于:在聚类过程中迭代地对数据集进行划分的同时优化各个簇类所在的子空间,并且除了簇类数以外无需用户额外输入其它任何参数。通过在实际数据集上的实验结果表明,与其它软子空间聚类算法相比,SCFO算法能够获得更好的聚类效果。
1 相关研究
软子空间聚类与传统聚类方法不同,为了衡量属性(特征)与簇类的相关性,软子空间聚类在聚类过程中赋予簇类中的各维度属性一个权值。通常,在一个簇类中的每一维属性与簇类具有不同的相关性[2],因此,在聚类过后各簇类所在的子空间可以通过特征权值来识别。软子空间聚类就成为目前高维数据聚类分析的研究热点[2,7,9-10]。
在详细介绍相关工作之前,首先对全文所使用的符号进行说明。文中,记DB={x1,…,xi,…,xN}为数据集,V={vkj}C×D为簇类中心矩阵,U={uki}C×N为隶属度矩阵,W={wkj}C×D为权值矩阵。其中,C是簇类数,D是数据集中样本点的维数,xij表示样本xi的第j维属性值(j=1,2,…,D),vkj是第k个簇中心点的第j维属性值,uki是第i个样本对第k类簇的隶属度,wkj表示第j维属性与第k个簇类的相关程度,wkj的值越大代表相关性越强。
Gan[9]等提出了一种处理高维数据聚类的软子空间聚类算法FSC。该算法定义了模糊权值,并将模糊权值引入到k-均值聚类算法的目标函数中,进而确定了以下目标函数:
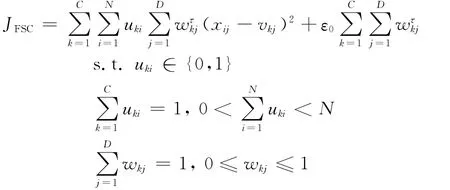
其中,ε0的引入是为了避免FSC算法在聚类过程中可能出现除以零的错误,τ是模糊因子。对数据集DB进行划分后,FSC算法使用下式更新权值:
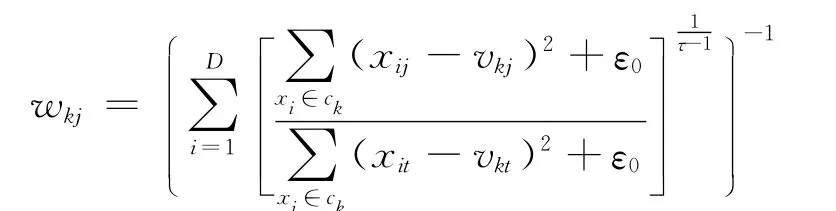
从上式可以看出,FSC算法的模糊权值更新方式类似于模糊k-均值聚类算法的模糊隶属度的加权方法。同时,观察上式可以发现在同一个簇类中,赋予每一维属性的权值与该属性上的数据分散程度成反比,某一维属性上的数据越分散,其被赋予的权值越小,反之亦然。FSC算法首先初始化簇中心,然后迭代地更新权值矩阵W和聚类中心矩阵V,直到满足结束条件。为了避免在权值计算中加入ε0,Jing[2]等提出了另一种软子空间聚类算法EWKM,其目标函数定义如下:

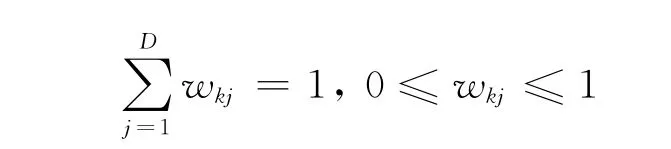
其中,目标函数的第1项为簇内紧凑度,第2项为权值熵;γ是用户输入的参数,其引入的目的是为了在聚类过程中平衡熵对权值的影响。假如参数γ值很大,各个簇类中的每一维度属性被赋予的权值将基本相同。因此,通过熵的引入,EWKM算法能够有效地控制簇类中各属性被赋予的权值。但是从以上算法可以发现,这些算法在聚类过程中更多的是针对簇类的簇内紧凑度问题,并未考虑对子空间进行优化,从而在一定程度上影响了算法的聚类精确度。
综合FSC算法和EWKM算法,文中定义了衡量特征权值分布的新指标,并与簇内紧凑度相结合构造了一个新的目标函数,以此为基础提出一个新的软子空间聚类算法SCFO。新算法采用类似于k-均值的算法结构,迭代地优化目标函数,以获得更高的聚类精度。
2 SCFO算法
2.1 目标优化函数
在软子空间聚类方法中关于特征加权有如下特点:在同一个簇类中,各维度属性的权值与该维度属性的数据分散程度成反比[2],即某个维度上的数据越集中,则该维度属性的权值越大,体现了该维度属性对簇类越重要。因此,从一定程度上特征权值的大小反映了该属性上数据的分散程度,而特征权值的分布越集中越体现了簇类所在的子空间越优化[7]。在满足wk1+wk2+…+wkD=1的条件下,文中给出如下公式,用于衡量特征权值的分布情况:
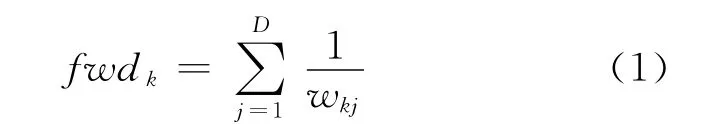
根据式(1)可知,特征权值分布越均匀,fwdk值越小。与大多数传统聚类算法一样,考虑各个属性与簇类的重要程度都相同的情况下,即∀j,j=1,2,…,D,wkj=1/D,fwdk获得最小的值。基于式(1),文中算法的目标函数采用了类似EWKM算法的形式。构造目标函数具体如下:
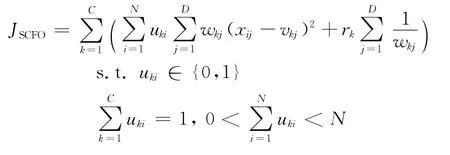

其中,目标函数的第1项是加权的簇内紧凑度之和;系数rk用来平衡簇内紧凑度和特征权值分布对目标函数的影响。参考文献[7],文中将系数rk的值设置为:
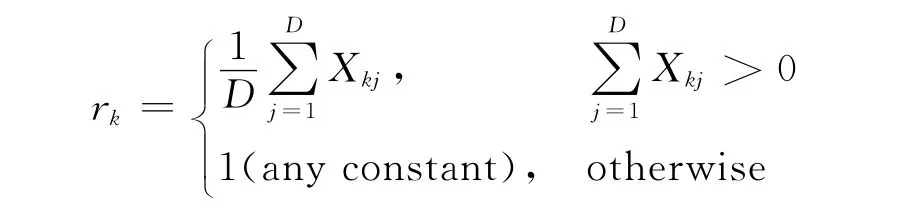
上式中Xkj是引入的新记号,Xkj定义为:
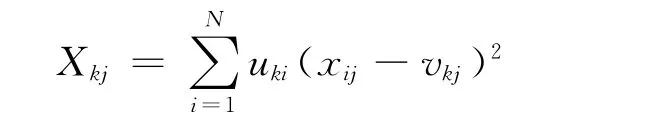
利用拉格朗日乘子优化方法最小化目标函数JSCFO,获得了SCFO算法隶属度uki,聚类中心vkj和特征加权wkj的迭代计算公式,见定理1。
定理1 给定rk,最小化SCFO算法的优化目标函数JSCFO,当且仅当:
1)隶属度uki的迭代计算公式为:

2)聚类中心vkj的迭代计算公式为:

3)特征加权wkj的迭代计算公式为:
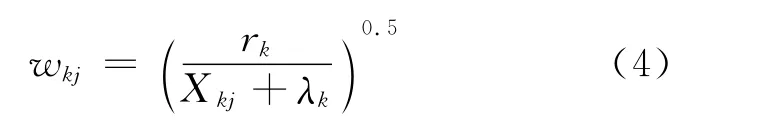
式中:λk——拉格朗日乘子。
定理1的证明过程可以参考文献[2,9-10]。
定理2 在区间(-MIN_Xk,+∞)内,存在唯一的λk使式(5)成立。其中MIN_Xk表示Xkj(j=1,2,…,D)中的最小值。
证明 在满足wk1+wk2+…+wkD=1的条件下,结合特征加权wkj的迭代计算式(4),获得λk的约束方程如下:和,因此存在唯
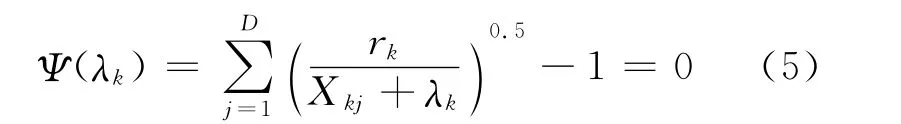
基于上述约束方程,可证得λk在区间(-MIN_Xk,+∞)内Ψ(λk)单 调 递 减,且一的λk使得式(5)成立,从而定理2得证。此外,一般可以采用牛顿法[12]求解方程(5)。
2.2 SCFO算法过程和分析
SCFO算法根据式(2)~式(5)最小化目标函数JSCFO,具体算法描述如下:
输入:簇类个数C;随机选择C个初始聚类中心并设置所有的特征权值初始值均为1/D;
重复:
根据式(2),更新隶属度矩阵U;
社区教育部门开展的非物质文化遗产传承与创新活动采取线上、线下、线上与线下混合式、体验式的网络直播、远程讲堂与培训、非物质文化遗产进学校等多种方式,如下表。
根据式(3),更新簇类中心矩阵V;
根据式(5),利用牛顿法求解每个簇类对应的拉格朗日乘子;
根据式(4),更新权值矩阵W;
算法结束:直到目标函数值达到最小值或V和W在迭代过程中相邻两次的变化小于给定的阈值;
输出:最终的聚类中心矩阵V和隶属度矩阵U。
SCFO算法采用了类似于k-均值聚类的算法结构,在聚类过程中额外增加了计算特征权值的步骤,并且对每个迭代步骤使用的更新公式进行了重新定义,因此SCFO保留了k-均值聚类算法的收敛性。假设SCFO算法需要P次的循环迭代才能满足结束条件,通过分析SCFO算法的每个执行步骤,可以获得算法的时间复杂度为O(KNDP)。因此,SCFO算法与k-均值聚类算法的时间复杂度相同。
3 实验结果与分析
为了检验SCFO算法的性能,文中对SCFO算法和FSC[10]、EWKM[2]、FWKM[9]以及ASC[7]聚类算法进行比较。对于这些算法的参数设置,这里采用各文献的建议。例如,对于EWKM算法的γ,根据建议设定为0.5;FSC算法的τ根据文献[10]设定为2.1;FWKM算法的β设定为1.5;SCFO算法与ASC算法一样,除了簇类个数K,无须用户输入额外参数。实验计算机配置采用Intel®Core(TM)i5-3470CPU@3.20GHz,4G内存,仿真软件为Eclipse3.5。
3.1 聚类性能指标
为了评估聚类效果,文中采用互信息NMI[13]和Rand指数(RI)[14]两个聚类性能指标对实验结果进行评价,公式如下:
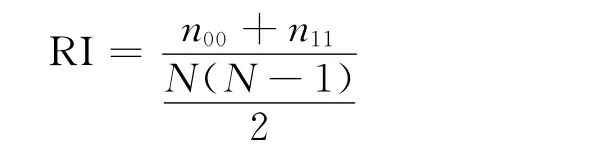
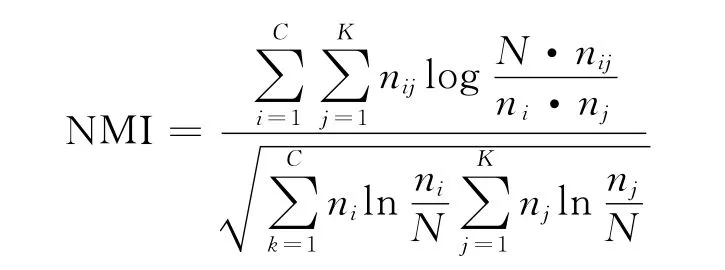
式中:K——聚类数;
n00——各样本不属于同一簇类并被划分到不同聚类结果的样本点数量;
n11——各样本属于同一簇类并被划分到相同聚类结果的样本点数量;
nij——属于类i并被分配到簇类j的样本数目;
ni——属于类i的样本数目;
nj——属于簇j的样本数目。
根据以上公式可知,RI和NMI这两个指标的值均落在区间[0,1]中,指标值越大表示算法的聚类效果越好,反之亦然。当上述两个性能指标的值均为1时,聚类算法将完全正确的识别出数据集中的每个簇类。
3.2 实验数据集
为了检验SCFO算法的有效性和聚类精度,文中采用来自于UCI的7个数据集:Wisconsin Breast Cancer(WBC)、Waveform、Semeion、SPECT、Spambase、Wine和Mfeat。其中WBC和Wine这2个低维数据集主要用于评估聚类算法对低维数据集的兼容性。数据集的详细信息见表1。
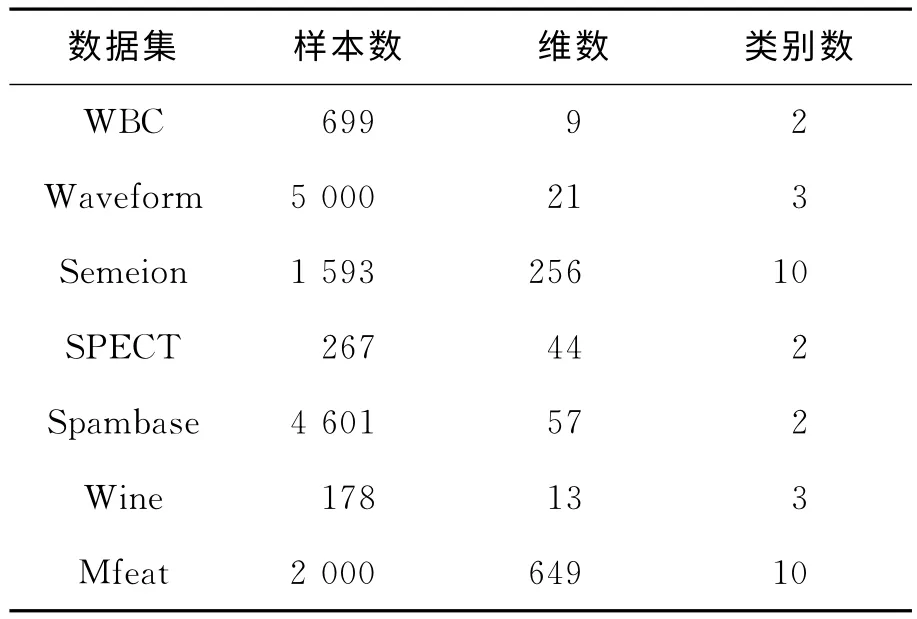
表1 实验数据集的详细信息
3.3 实验结果聚类性能指标
文中选取了UCI的7个数据集进行对比测试。对于所有的实验数据集,文中使用最小最大规范化处理,使得实验数据集中的各属性值均落在区间[0,1]中。同时,为了保证实验的公平性、代表性,避免极端情况的出现,每一个算法均独立运行20次,最后取20次实验结果的平均精度和方差,聚类结果分别见表2和表3。
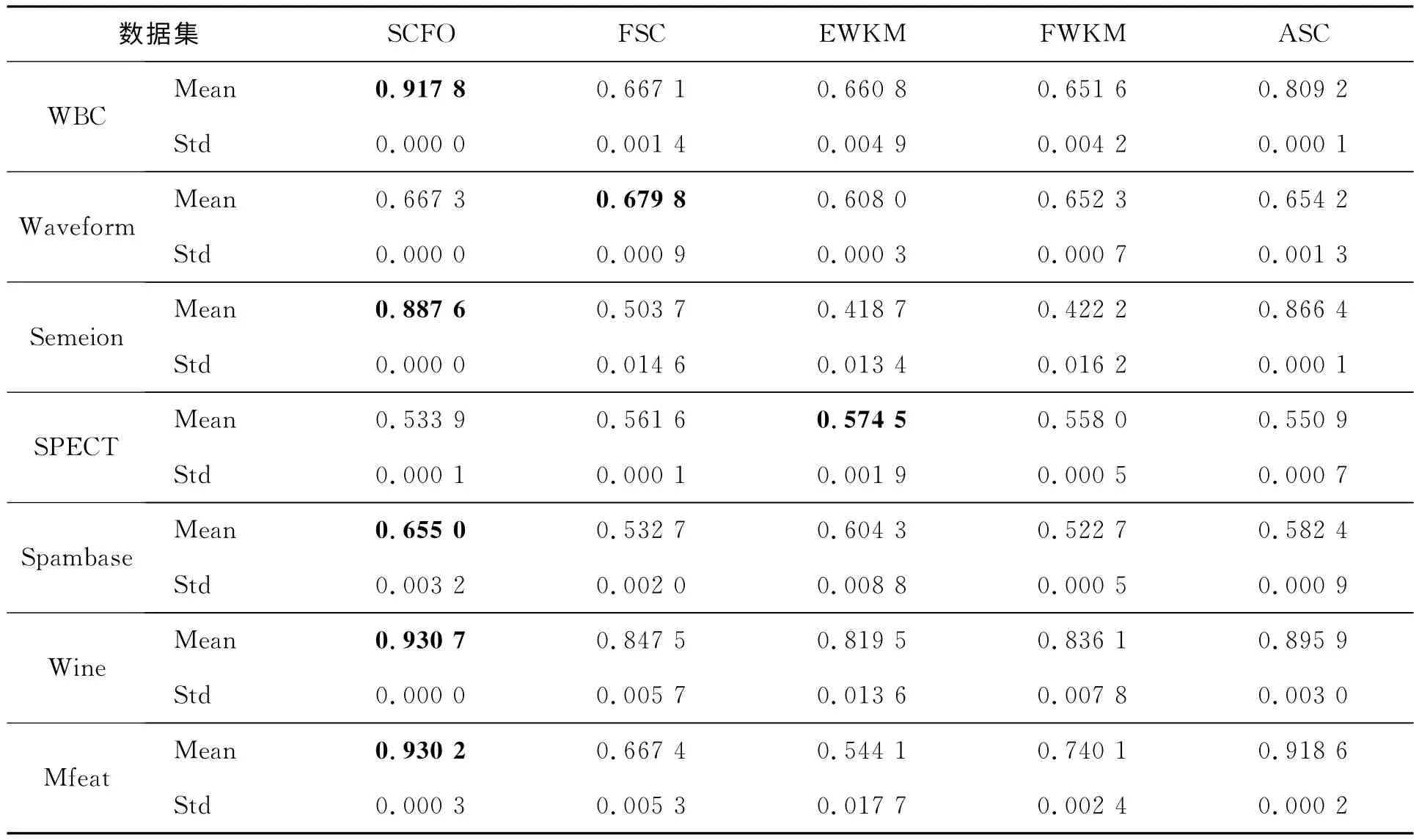
表2 SCFO以及其它4种算法20次运行的实验结果(RI指标)

表3 SCFO以及其它4种算法20次运行的实验结果(NMI指标)
从表2和表3给出的聚类结果来看,显然在UCI的7个数据集上,SCFO算法相比其它4种算法获得了最好的聚类划分结果;FSC、EWKM和FWKM算法的聚类质量基本相同,而ASC的聚类质量优于FSC、EWKM和FWKM算法。这是因为ASC与SCFO算法一样,在聚类过程中不仅考虑了数据集划分的优化,而且对各个簇类所在的子空间也进行了优化。对比表2和表3,可以观察到算法在某个数据集上获得最高的RI值,但其对应的NMI值却不一定最高,即一个表现出高精度的聚类算法可能拥有很大的RI值,而可能没有一个高的NMI值。因此,检验算法的聚类性能通常需要不同的评价指标来评估。
SCFO以及其它4种算法20次运行的平均时间见表4。
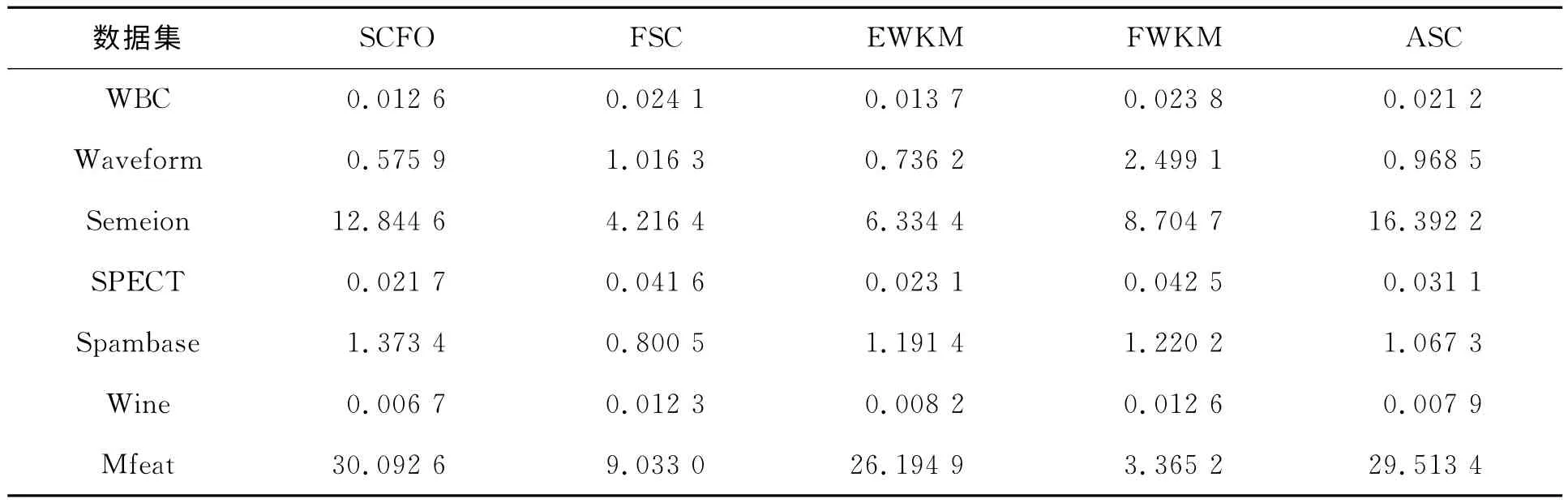
表4 SCFO以及其它4种算法20次运行的平均时间 s
表4记录了SCFO、FSC、EWKM、FWKM以及ASC这5种算法在UCI的7个数据集上聚类所需要的平均运行时间。对比SCFO和其它4种算法,可以发现新的基于特征加权优化的软子空间聚类算法SCFO并不会对算法的运行时间带来明显影响。我们注意到SCFO算法和ASC算法在Mfeat和Semeion这两个高维数据集上的运行时间大于其它3种聚类算法,这是因为SCFO算法和ASC算法在聚类过程中增加了求解各个簇类对应的拉格朗日乘子的步骤。该步骤导致了算法在高维数据集上需要耗费更多的运算时间,但其有效地增强了算法的自适应能力,一定程度上提高了算法的聚类精度。
4 结 语
提出了一种新的基于特征加权优化的软子空间聚类算法SCFO,用以解决高维数据的聚类问题。与传统的软子空间聚类算法相比,SCFO算法在聚类过程中考虑了数据集划分和各簇类所在子空间两方面的优化,除了簇类个数K,SCFO算法无需用户预先输入其它任何参数。通过在UCI的7个数据集上的实验结果表明,SCFO算法相比于FSC、EWKM、FWKM和ASC,能够获得更好的聚类质量。为了能够进一步获得更好的聚类效果,今后的研究将考虑对SCFO算法平衡目标函数中的前后两项的系数进行优化。
[1] Moreno-Hagelsieb G,Wang Z,Walsh S,et al.Phylogenomic clustering for selecting non-redundant genomes for comparative genomics[J].Bioinformatics,2013,29(7):947-949.
[2] Jing L,Ng M K,Huang J Z.An entropy weighting k-means algorithm for subspace clustering of highdimensinoal sparese data[J].IEEE Transactions on Knowledge and Data Engineering,2007,19(8):1-16.
[3] Tang L,Liu H,Zhang J.Identifying evolving groups in dynamic multimode networks[J].IEEE Transactions on Knowledge and Data Engineering,2012,24(1):72-85.
[4] Huang J Z,Ng M K,Rong H,et al.Automated variable weighting in k-means type clustering[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2005,27(5):657-668.
[5] Parsons L,Haque E,Liu H.Subspace clustering for high dimensional data:a review[J].ACM SIGKDD Explorations Newsletter,2004,6(1):90-105.
[6] Aggarwal C C,Wolf J L,Yu P S,et al.Fast algorithm for projected clustering[C]//Proceeding of ACM SIGMOD.1999:61-72.
[7] 陈黎飞,郭躬德,姜青山.自适应的软子空间聚类算法[J].软件学报,2010,21(10):2513-2523.
[8] 毕志升,王甲海,印鉴.基于差分演化算法的软子空间聚类[J].计算机学报,2012,35(10):2116-2128.
[9] Jing L,Ng M K,Xu J,et al.On the performance of feature weighting k-means for text subspace clustering[C]//Proceeding of WAIM.2005:502-512.
[10] Gan G,Wu J,Yang Z.Fuzzy subspace algorithm for clustering high dimensional data[C]//Proceeding of ADMA.2006:271-278.
[11] Chu Y H,Chen Y J,Yang D N,et al.Reducing redundancy in subspace clustering[J].IEEE Transactions on Knowledge and Data Engineering,2009,21(10):1432-1446.
[12] Xue Y.Optimization theory and method[M].Beijing:Beijing University of Technology Press,2001.
[13] Liu J,Mohammed J,Carter J,et al.Distancebased clustering of CGH data[J].Bioinformatics,2006,22(16):1971-1978.
[14] Rand W M.Objective criteria for the evaluation of clustering methods[J].Journal of the American Statistical Association,1971,66(336):846-850.

