基于模糊控制的12脉波整流器动态性能改善

张俊双，高俊虎，江翼

（1.国网内蒙古东部电力有限公司电力科学研究院，内蒙古呼和浩特010020；2.西安交通大学电气工程学院，陕西 西安710049；3.哈尔滨工程大学自动化学院，黑龙江 哈尔滨150001；4.国网电力科学研究院武汉南瑞有限责任公司，湖北 武汉430074）

整流器是利用晶闸管、IGBT 等电力电子器件将交流电变换为直流电的装置，也称为AC/DC变换装置。AC/DC变换装置广泛应用于冶金、化工、电源等行业。

为了提高输出功率并减少谐波的产生，AC/DC 装置往往采用多重化电路结构，将多个整流桥串并联。此外，为了提高输出直流电能的质量，AC/DC 变换装置往往还会安装RC 滤波电路。由于AC/DC 变换装置本身为典型的非线性系统，在增加滤波环节后，系统对负载扰动更加敏感。以不间断电源（uninterruptible power supply，UPS）为例，其实质为交-直-交电路，也即AC/DC 而DC/DC 与DC/AC 装置为变结构系统，它们可视为AC/DC 变换装置的部分负载。负载大范围变化时，传统的PID 控制很难得到良好的动态性能。

本文在分析12 脉波整流电路数学建模的基础上，采用模糊控制作为AC/DC 变换装置的控制策略，并在Matlab/Simulink环境下分别对基于PID、模糊控制方法的整流器进行了仿真，并对基于模糊控制方法的整流器进行了实验验证。

1 12脉波整流电路的数学模型

如图1 所示为12 脉波相控整流电路的拓扑结构图。整流器输出电压UDC的平均值可写为［1］

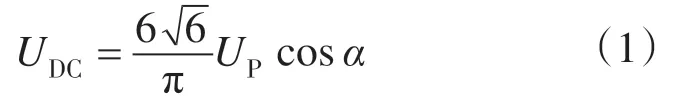
式中：α为晶闸管的触发角；UP为三相交流电源的有效值。

在控制系统中，α的值可由控制电压决定，其关系可表示为

式中：uc为控制电压；ucmax为控制电压允许的最大值。由式（1）、式（2）可知，整流器的增益KR由下式决定：

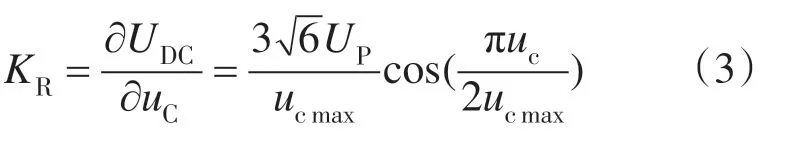
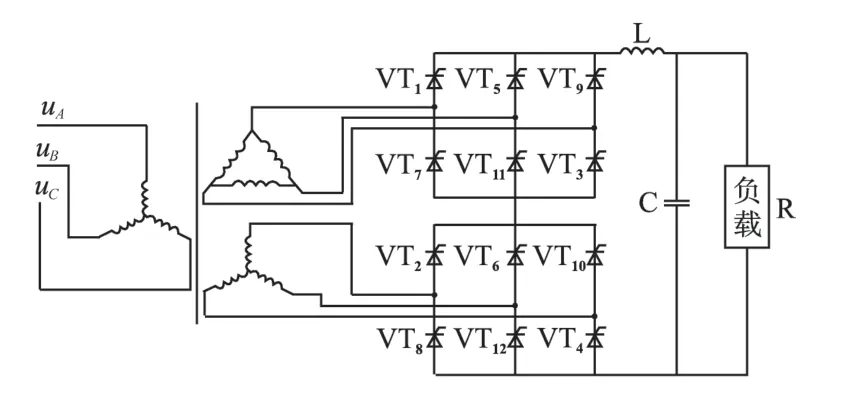
图1 12脉冲相控整流电路Fig.1 12-pulse phase controlled rectifier

由于失控时间的存在，整流器还包括一个具有平均值T/24 的延迟环节，其中T 为电源周期。加入延迟环节后，整流器传递函数GR(s)可表示为

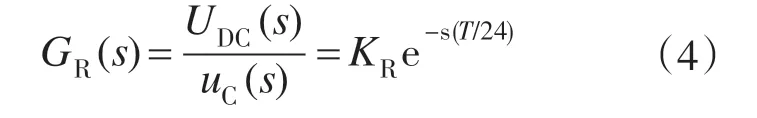
由式（3）、式（4）可知，整流器的增益随着输入电压的改变而变化并伴有输出延迟。所以，12脉波整流电路为非线性系统。

整流电路的输出经过滤波电路处理后，才能送给负载，滤波器经常采用如图1 所示的LC 电路，其传递函数表示为

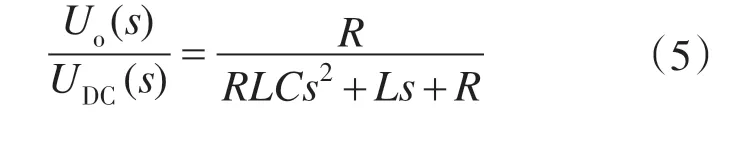
式中：Uo为负载电压，即控制系统的输出。

在12脉波整流控制系统中，输出电压作为反馈量，与给定信号一起输入到控制器中，以实现输出可控。系统的方框图如图2所示。

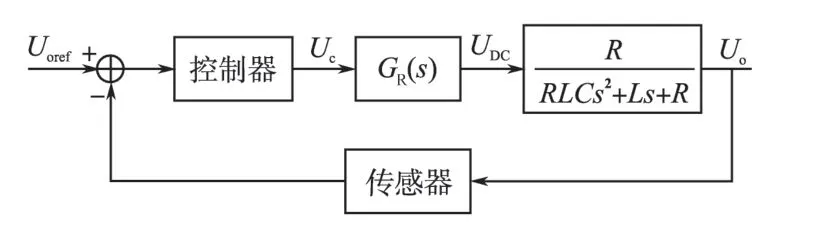
图2 12脉波整流控制系统框图Fig.2 The diagram of 12-pulse rectifier control system

2 控制策略研究

2.1 系统参数与指标

系统中滤波电感与滤波电容的大小可根据下式的计算来选择［2］：

式中：vo为滤波后的脉动电压；vL为滤波前的脉动电压；fr为直流电压脉动频率。

使用该公式的前提为R ≫1/2πfrC。

在12脉波整流系统中，要求输出电压的范围是800～1 000 V，如果滤波要求在该范围内，输出给负载的电压脉动率为2%，则根据计算，选取L=1 mH，C=825 μF。

2.2 模糊控制器设计

2.2.1 模糊控制器的基本结构

模糊控制方法由于对控制对象数学模型的精确性要求不高，能够处理非线性问题，因而得到广泛的应用。对12 脉波整流控制系统采用模糊控制，能够得到较理想的控制性能。

2.2.2 控制器的输入输出

控制器结构如图3 所示，令给定与反馈之间的误差信号及其变化率作为模糊控制器的输入。控制器的输出为晶闸管的控制角变化量，需要在输出端增加积分环节，来计算出实际的控制角以直接生成触发信号。

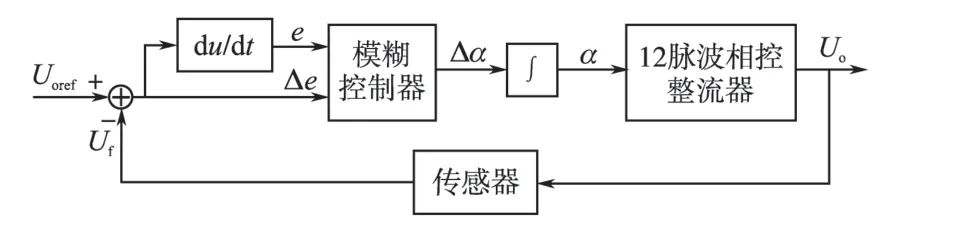
图3 模糊控制系统结构图Fig.3 The structure diagram of fuzzy control system

2.2.3 输入与输出的模糊化

将每个输入与输出变量都分别定义正大（PB），正小（PS），零（ZE），负小（NS），负大（NB）这些模糊集合。

对于误差e，根据系统的输出范围，可以将200 V的误差范围定义为NS与PS，以优化动态性能，模糊集ZE应尽量小，以提高系统精度。对于误差变化率Δe，应参照系统的动态性能指标来设置。对于输出变量Δα，根据控制角移相范围是0°～120°及系统响应速度来调整。在增加量化因子和比例因子后，分别设置误差e 的论域为［-10，10］，误差变化率Δe 的论域为［-100，100］，输出Δα的论域为［-120，120］。

根据个人经验与不断的调试优化，得出各个变量的隶属函数如图4所示。

图4 隶属函数Fig.4 The membership function

2.2.4 控制规则与解模糊

在进行规则的设置时，利用个人的操作经验，可对控制规律进行以下概括。

如果误差为负，且误差变化率为负，则增大控制角，减少输出电压；如果误差为正，且误差变化率为正，则减小控制角，增大输出电压。

对以上的经验进行总结并反复调试，得到表1所示的语言控制规则。

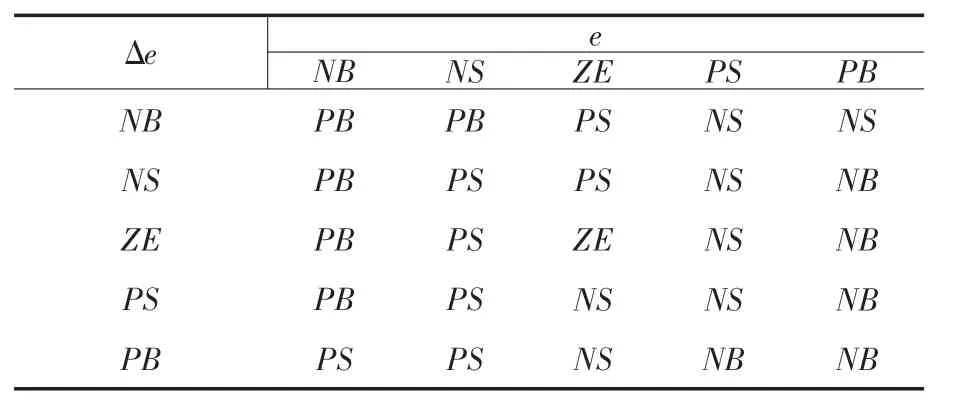
表1 语言控制规则Tab.1 Linguistic control rule

模糊控制器的输出结果能够由表1中的控制规则，利用最小—最大推理方法计算得到。最后利用面积中心法进行解模糊计算，得到精确的输出数值。

2.2.5 消除稳态误差

稳态误差是模糊控制固有的缺陷，通过以上所述设计的控制系统，会有10 V 左右的稳态误差。可以通过增加控制规则，来消除稳态误差。如果给定与反馈的误差大于10 V，则系统处于动态调节状态，此时采用表1 所示的规则进行控制动作。如果误差小于或等于10 V，可视为系统处于稳态微调状态，此时采用额外的控制规则。在工程上，控制角的分辨率可设置为0.1°。以此作为控制幅度，设置如下的控制规则：如果误差为负，控制角增大0.1°。如果误差为正，控制角减小0.1°。

这样，在误差变量中以10 V 作为阈值，使控制器在动态调节与稳态微调这两个状态之间进行切换，可以保证系统稳态误差减小到性能指标的要求范围内。

3 仿真及实验结果分析

3.1 PID控制器仿真

在Matlab/Simulink 环境下对采用本文设计的模糊控制整流器进行仿真，搭建如图5 所示的仿真系统，并与同样条件下传统PID 控制整流器进行对比。

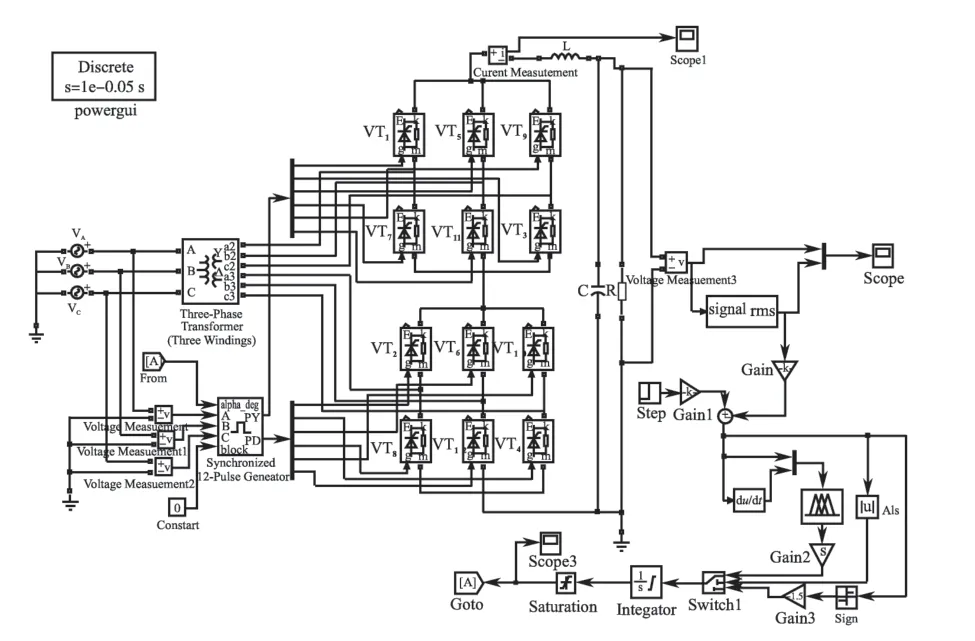
图5 Matlab/Simulink仿真图Fig.5 Matlab/Simulink simulation map

根据图2 所示的系统框图，当负载大小变化时，系统的开环极点也相应变化。图6 为利用PID控制，负载分别为2.5 Ω和10 Ω时系统的波特图，图7 为不同负载情况下系统输出从0 V 上升到800 V 的动态曲线，其中控制参数P=0.22，I=15，D=0.01。由曲线可知，当PID 的参数不改变，如果负载由2.5 Ω变为10 Ω，系统的输出在稳态时会产生小幅的振荡，这显然不利于负载的工作。如果采用PID 控制，想要系统具有良好的动态性能，PID的参数必须随时调节，否则系统的输出响应无法满足负载要求。

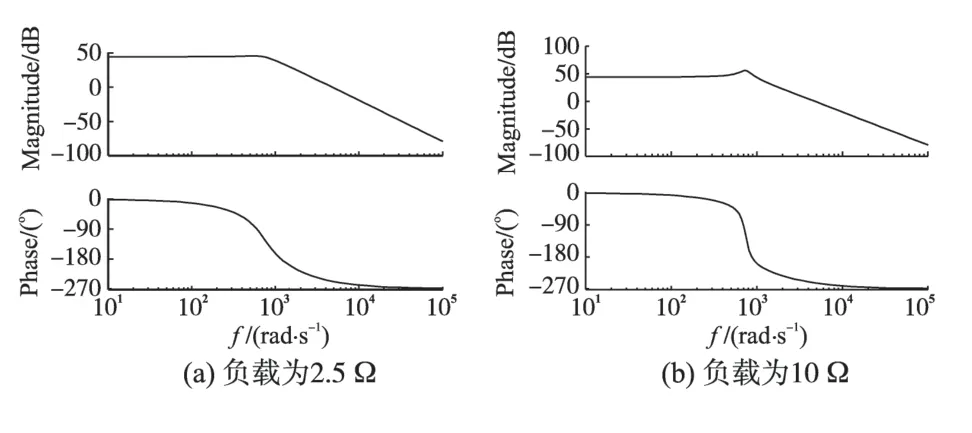
图6 系统波特图Fig.6 The bode plot

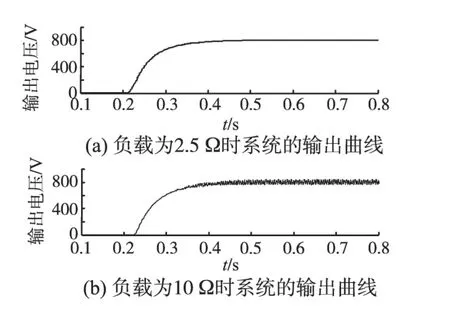
图7 不同负载情况下PID控制输出曲线Fig.7 PID control output waveforms in different loads

3.2 模糊控制器仿真

图8 为采用模糊控制时，不同负载情况下的系统输出曲线。与图7 比较可知，模糊控制对负载变化的适应性明显增强，负载变化时，没有影响系统的动态性能。

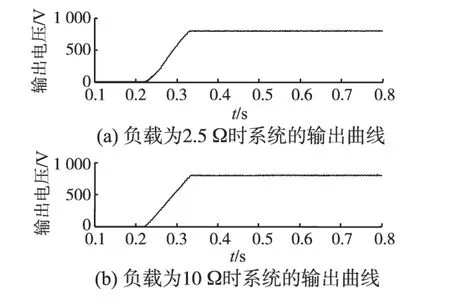
图8 不同负载情况下模糊控制输出曲线Fig.8 Fuzzy control output waveforms in different loads

3.3 两种控制器的性能比较

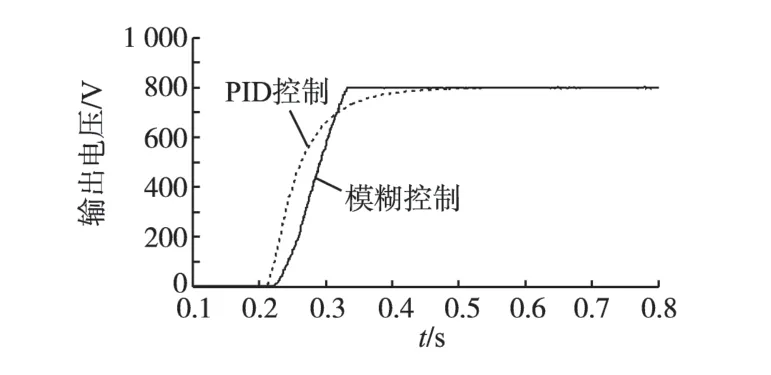
图9 PID控制与模糊控制仿真曲线比较Fig.9 PID control and fuzzy control waveforms comparison

图9 为同样负载条件下，PID 控制与模糊控制的系统输出曲线比较。其中实线为模糊控制时系统的输出曲线，虚线为PID 控制时系统的输出曲线。从图9中可知，模糊控制的响应速度总体上优于PID控制，使系统的动态性能有很大改善。

3.4 模糊控制器实验结果

本文搭建了以TMS2812为控制芯片、晶闸管为电力电子器件的12脉波整流器实验平台，其功率为25 kW。图10a为模糊控制的12脉波整流电路输出电压由800 V上升至1 000 V的动态波形，图10b 为模糊控制的12 脉波整流电路输出电压由1 000 V下降至800 V的动态波形。

图10 动态波形Fig.10 Dynamic waveform

由图10 可知，采用模糊控制的12 脉波整流器具有调节速度快、调节精度高的优点。由于模糊控制器调节速度快于PI控制器，导致晶闸管开关频率在一定程度上有所提高，因此实验波形中含有较高的高频分量。

4 结论

本文采用模糊控制作为12 脉波整流器的控制方法，解决了PID控制由于系统的非线性特点，对负载变化适应性差的问题。仿真及实验结果表明，模糊控制可以克服负载变化对系统的影响，具有响应快、超调小，对负载变化适应性强的优点。与传统PID控制相比，12脉整流器的动态性能得到了较好的改善。

［1］ 陈伯时.电力拖动自动控制系统—运动控制系统［M］.第3版.北京：机械工业出版社，2006.

［2］ Muhammad H Rashid.电力电子技术手册［M］.北京：机械工业出版社，2004.

［3］ 石辛民，郝整清.模糊控制及其MATLAB仿真［M］.北京：清华大学出版社，2008.

［4］ 台广锋，潘社卫，郭鑫，等.模糊PI 控制在变频调速系统中的应用［J］.矿冶，2009，18（4）：72-75.

［5］ 雷惠，庄斌星.晶闸管整流电源负载特性的研究［J］.电力电子技术，1999，10（1）：45-47.