计算长电缆电机端电压的递推算法

俞光

（南京工程学院工业中心，江苏南京211167）

在风力发电等大功率场合，变流器与电机间通常由上百m的长线电缆连接，而变流器输出电压为上升时间仅几μs 的调制波，经过长线电缆传输后，在电机端发生反射现象［1-4］，导致机端过电压问题［5-7］，最严重的情况下机端电压会达到变流器输出电压的2倍，威胁绕组绝缘，以及带来严重的电磁干扰［8-9］。

在电机端进行阻抗匹配能有效抑制过电压，但是安装不方便。目前最常见的处理方法是在变流器中安装RLC滤波器［10-17］，以滤除调制波的陡峭上升沿，使得变流器的输出电压具有一定的上升时间。理论分析和实践已验证该方法的确可以起到抑制电机端过电压的效果，但抑制效果与滤波器输出电压的上升时间具有密切联系。因此研究电机端电压的大小与上升时间的关系具有重要意义。

文献［9-12］根据均匀传输线和反射理论进行定性分析，给出了在变流器输出电压为梯形波情形下电机端电压的反射过程，但在上升时间是多次传输时间时，反射理论分析显得非常困难，而且很难得到电机端电压在整个时域上的表达式。文献［18-20］根据拉普拉斯变换或时域法求解了传输线路上的波函数。然而，没有具体针对变流器输出的梯形调制波，准确给出电机端电压在整个时域的具体表达式，以及关于极端电压收敛性、最大值等详细特性的严格论证。

本文首先给出一般形式的电机端电压和变流器输出电压的时域关系，即电机端电压的递推关系。然后针对变流器输出电压为梯形波的情形，推导电机端电压关于上升时间的表达式，求出其最大值并指明其振荡周期和收敛性。最后通过在MW级双馈风力发电实验台，测出电机端电压波形，再与基于本文提出的理论仿真结果进行对比，说明我们的理论分析具有一定的实际指导意义。

1 电机端电压递推关系的推导

变流器与电机间由电缆线路连接，见图1。

将电缆线路看成是无损均匀传输线［7］，设电缆的单位长度电感为L0，单位长度电容为C0，位置x 表示从电缆中某点到变流器输出端的距离，电机端到变流器的总距离为l。由电路原理可知，位置x 处运算形式的电压U( x,s )和电流I( x,s )关系为［18］

其中U′(s )和U″(s )需由边界条件确定。

当电机端等效为阻抗ZL时，变流器端边界条件为：U( 0,s )=U1(s )，电机端边界条件为：ZLI( l,s )=U( l,s )。于是得［1］：

式中：τ 为单程传输时间；Z0为电缆的特性阻抗。由式（3）可得：

式中，r 为反射系数。当r=1 时，相当于电机端开路；当r=-1 时，相当于电机短路；其它情况-1 ＜r ＜1。这里假设反射系数为一常数，即不含有运算算子s，对于变流器经长线驱动电机系统而言，电机对于调制电压呈高阻抗特性，反射系数一般在0.9附近［12］。

根据式（3）可求得运算形式的电机端电压和变流器输出电压的关系为

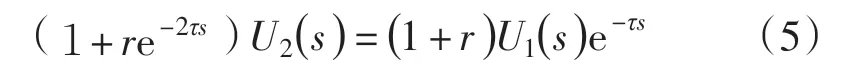
根据拉普拉斯变换的延时性质，对式（5）进行拉普拉斯反变换，可得时域中电机端电压的递推关系为

该式的含义是：当前时刻的电机端电压等于单程传输时间前的变流器输出电压的(1 +r )倍减去往返传输时间前的电机端电压的r 倍。

2 递推算法

我们称根据式（6）计算电机端电压的方法为递推算法。在递推的初始段，即当t ≤τ 时，变流器输出电压还没有传到电机端，故u2(t )=0。根据递推关系式（6）可得，当( 2k -1) τ ＜t ≤( 2k +1) τ时，u2(t )的级数表达式为

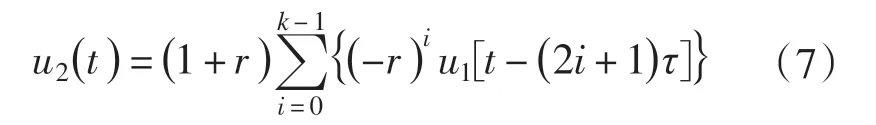
式中：k=1,2,…。

这就是时域下电机端电压关于变流器输出电压的表达式。

当变流器输出电压为梯形波时，两端各为一个斜坡阶跃，因此分析一个斜坡阶跃的响应即可。此时，变流器输出电压可由分段函数表示，即

其中 2( m-1) τ ＜tr≤2mτ m=1,2,…

式中：Ud为梯形波的平稳段电压值。

下面根据式（7）求解电机端电压的显式表达式。

当k ＜m，且( 2k -1) τ ＜t ≤( 2k +1) τ 时，对于i=0,1,…,k-1 均有t-( 2i+1) τ ＜tr，因此：

当k ≥m，电机端电压需要表示为分段函数的形式。可把区间[( 2k -1) τ,( 2k +1) τ]分成如下两段：

当( 2k -1) τ ＜t ≤tr+2( k- m )τ+v 时，

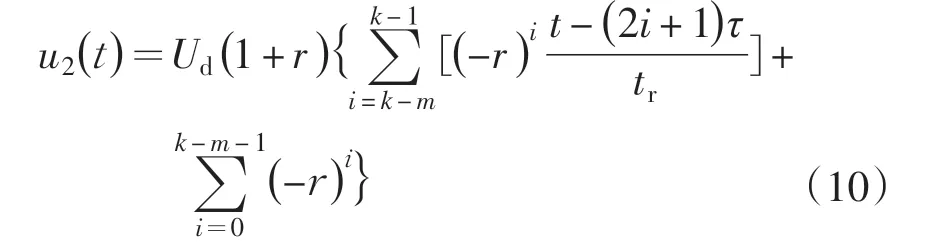
当tr+2( k- m )τ+τ ＜t ≤( 2k +1) τ 时，

综上所述，式（9）～式（11）包括了电机端电压在整个时域上的表达式。当 |r |＜1 时，上述级数是收敛的，且u2(∞ )=Ud。

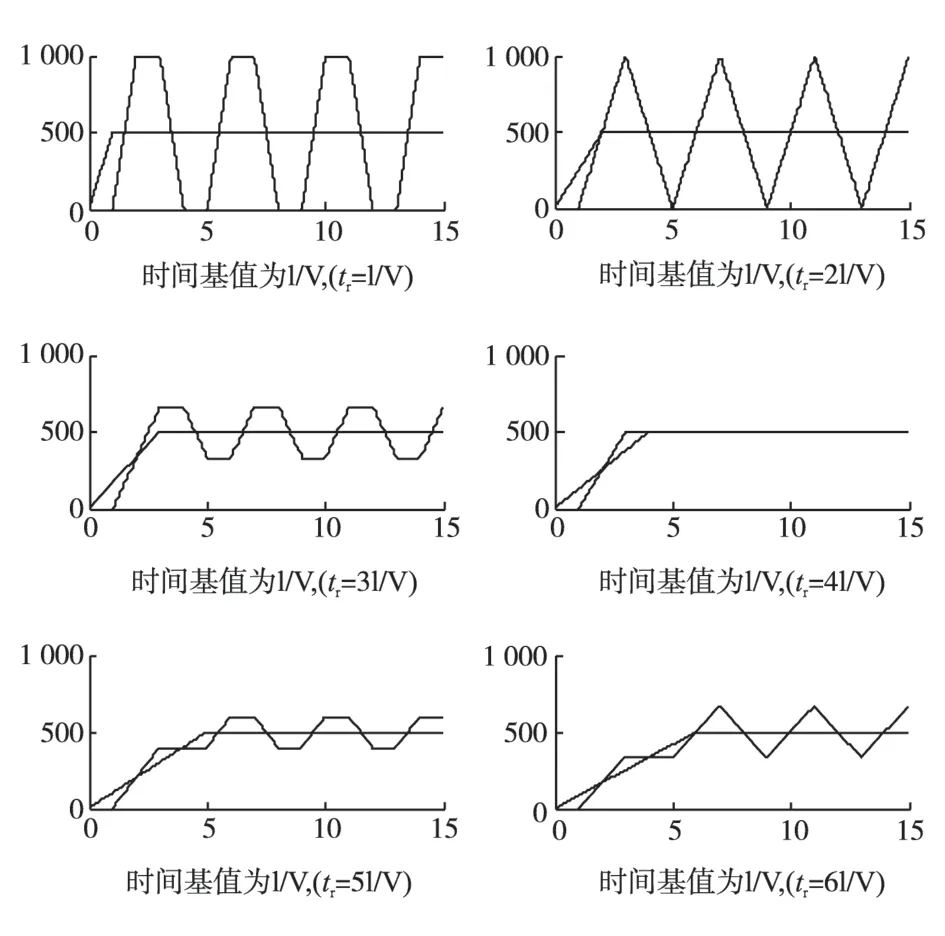
图2 反射系数为1不同上升时间下的电机端电压斜坡阶跃响应Fig.2 Trapezoidal response curves of motor terminal voltage with different rise-time when r=1

图2 为反射系数为1，变流器输出电压在不同的上升时间下，电机端电压的波形，虚线为变流器输出的梯形波，实线为电机端电压。横坐标为传输时间，单位为单程传输时间次数，纵坐标为电机端电压值，单位为V。可看出，在反射系数为1 的情形下，电机端电压在上升时间之后围绕变流器输出电压振荡，振荡周期为4 倍单程传输时间。

3 电机端电压的最大值

根据电机端电压在整个时域上的表达式，可以求出其最大值。在-1 ≤r ＜0 的情况下，u2(t) 随时间单调递增至Ud，不存在电机端过电压现象。

在反射系数0 ＜r ≤1 的情况下，当t=tr+τ时，电机端电压取整个时域上的最大值，且最大值为

证明略。

特别地，若反射系数r=1，则

且m 为奇数时，

m 为偶数时

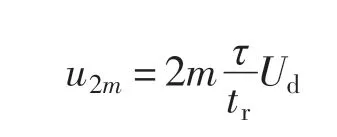
该结论对于涉及滤波器的输出电压上升时间具有重要意义。

从式（12）可看出，电机端电压最大值是上升时间tr的函数，如图3所示。

图3 电机端电压最大值与上升时间的关系Fig.3 Curves of the maximum motor terminal voltage versus rise-time

当m 为奇数时，电机端电压的最大值随tr的增大而增大，当m 为偶数时，电机端电压的最大值随tr的增大而减少。电机端电压的最大值随着tr的变化以4τ 为周期振荡。总之，为抑制电机端过电压，上升时间tr最好设置在4τ 的整数倍附近，并且倍数的取值越大抑制效果越好。

4 对比实验

为验证本文的分析方法符合实际系统，在2 MW 双馈风电发电机变流器试验台上进行现场实验，观测电机端电压的波形。

实验条件为：变流器输出端到电机转子端由长度50 m，每相4 根截面积为95 mm2的电缆，变流器的直流侧电压设定为550 V，调制出的线电压经过RLC滤波器得到变流器输出电压，试验电气连接图如图4所示。

图4 带RLC滤波器的双馈风力发电系统Fig.4 A doubly-fed wind-energy system with an RLC filter

通过改变RC 支路的参数，或拆除RC 支路，使得调制电压的上升时间发生改变，然后用示波器观测电机端电压的变化。图5所示波形对应的电感为0.07 mH，R为30 Ω，电容为0.1 μF，我们在示波器上测得的电机端电压的最大尖峰值约为650 V。

图5 有RC支路时电机端电压的实验波形Fig.5 Experimental wave of motor terminal voltage with RC

图6 所示波形对应于取消RC支路而保留滤波电感时的电机端电压，最大尖峰值为850 V。这两种情况的电机端电压相差很大的原因就是如果有电容的滤波作用，可使得电缆的输入电压具有较长的上升时间，与前文的分析结果是吻合的。从示波器上可以看到，在合理选择RLC参数的条件下，能将电机端电压的最大峰值降到比较小的值。

下面是按本文提出的迭代函数法得到的仿真波形，在仿真中使用的电缆线电磁波传输速度为v=1.5×108m/s。图7所示波形对应的电感为0.07 mH，R 为30 Ω，电容为0.1 μF 的情况，可以看出其形状与图5的波形类似。

图6 无RC支路时电机端电压的实验波形Fig.6 Experimental wave of motor terminal voltage without RC

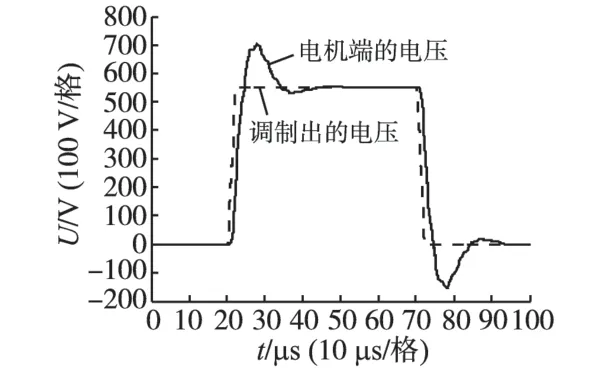
图7 有RC支路时电机端电压的仿真波形Fig.7 Emulation of motor terminal voltage with RC

图8 所示的仿真波形对应于取消RC支路而保留滤波电感，它与图6的实验波形类似。总之，虽然实验条件与仿真不可能完全一致，但从波形的相似程度来看，也说明本文的结论具有一定的意义。

图8 无RC支路时电机端电压的仿真波形Fig.8 Emulation of motor terminal voltage without RC

5 结论

本文推导出电机端电压与变流器输出电压的时域关系，并给出显式表达式及最大值，为电机端过电压抑制滤波器的设计提供了理论基础。

［1］ Skibinski G L，Kerkman R J，Leggate D，et al.Reflected Wave Modeling Techniques for PWM AC Motor Drives［C］//IEEE Conference on Applied Power Electronics Conference，Anaheim，1998：1021-1029.

［2］ 马文忠，李耀华，孔力，等.分布式电力系统中多脉宽调制电源激励下的波反射问题［J］.电网技术，2006，30（1）：19-22.

［3］ 马洪飞，徐殿国，陈希有，等.PWM逆变器驱动异步电动机采用长线电缆时电压反射现象的研究［J］.中国电机工程学报，2001，21（11）：109-113.

［4］ Paula H D，de Andrade D D，Chaves M L.Methodology for Cable Modeling and Simulation for High-frequency Phenomena Studies in PWM Motor Drives［J］.IEEE Transactions on Power Electronics，2008，23（2）：744-752.

［5］ Basavaraja B，Sarma V S S.Analysis of the Over-voltages in PWM-inverter Fed Induction Motors［C］//IEEE Conference on Asia-pacific Technology Conference，Gachibwoli，Hyderabad，2008：1-6.

［6］ 张兴，张显立，谢震，等.双馈风力发电变流器长缆驱动及其过电压抑制［J］.电力系统及其自动化，2006，30（21）：44-48.

［7］ 万健如，林志强，禹华军.高频PWM 脉冲波传输引起电机端子过电压的研究［J］.中国电机工程学报，2001，21（11）：43-47.

［8］ 潘启军，孟进，李毅，等.带交流励磁双变流器的双馈电机电磁干扰研究［J］.中国电机工程学报，2010，30（15）：80-86.

［9］ 张显立.风力发电用交直交变流器电磁兼容性设计［D］.合肥：合肥工业大学，2007.

［10］姜艳姝，于晓洋，齐路路.基于PWM 长线驱动系统模型的变频器输出RLC 滤波器设计［J］.中国电机工程学报，2010，30（36）：93-97.

［11］Jouanne A V，Enjeti P N.Design Considerations for an Inverter Output Filter to Mitigate the Effects of Long Motor Leads in ASD Applications［J］.IEEE Transactions on Industry Applications，1997，33（5）：1138-1144.

［12］杨淑英.双馈型风力发电变流器及其控制［D］.合肥：合肥工业大学，2007.

［13］Salomaki J，Hinkkanen M，Luomi J.Influence of Inverter Output Filter on the Selection of PWM Technique［C］//IEEE Conference on International Symposium Industrial Electronics.Montreal，2006：1052-1057.

［14］Chen X，Xu D，Liu F，et al.A Novel Inverter Output Passive Filter for Reducing both Differential and Common Mode du/dt at the Motor Terminals in PWM Drive Systems［J］.IEEE Transactions on Industrial Electronics，2007，54（1）：419-426.

［15］Pasterczyk R J，Guichon J M，Schanen J L，et al.PWM Inverter Output Filter Cost-to-losses Tradeoff and Optimal Design［J］.IEEE Transactions on Industry Applications，2009，45（2）：887-897.

［16］高强，马洪飞.PWM 逆变器端过电压滤波器设计［J］.电工电能新技术，2006，25（4）：27-29.

［17］张洪成.PWM 逆变器输入端及输出端滤波器的研究［D］.长春：吉林大学，2004.

［18］孙滔，刘宗行.无畸变传输线方程的解析解［J］.电路与系统学报，2007，12（6）：70-74.

［19］文磊.交流变频调速系统电机端电压量化分析及抑制方法［D］.南宁：广西大学，2009.

［20］卢斌先，王泽忠，程养春.基于拉氏反变换的传输线耦合电流半解析解［J］.电网技术，2007，31（14）：52-56.