一种多目标优化的非线性预测控制算法的研究

戴永彬

（辽宁工业大学软件学院，辽宁锦州121001）

预测控制算法被提出以来，在各个生产领域得到了广泛的应用。但是非线性预测控制在建模和优化求解等环节还有待深入研究［1］。由于非线性预测控制算法很难获得明确的解析式，所以采用常规的方法求解非常复杂。为了解决非线性预测控制算法的求解问题，研究人员提出了多种算法，粒子群被证明是有效的解决方案［2］。

预测控制算法是通过保证目标函数中的预测误差最小从而获取最优控制值。这是将目标函数作为单目标进行优化求解［3］。实际上，一个被控系统的多个输出变量的性能指标是不同的。因此，可以根据系统需求，设定不同的输出变量的预测误差的范围。这样，对非线性预测控制已由单目标优化求解变成为偏好的多目标优化求解。

近年来，多目标优化的进化算法获得了飞速发展，已有多种成熟的算法出现，例如NSGA-II，PAES，SPEA-II 等算法［4-6］。文献［7］将粒子群算法应用到多目标优化问题中，提出了MOPSO 算法。但是出于决策偏好或求解需要，决策者要求获取偏好区域的Pareto 解。为此，按照偏好方向将粒子种群引导至偏好区域，可以采用权重矩阵、参考点、参考区域、参考方向等引导方式［8］。目前，多数文献采用的引导形式是单一的，采用混合引导形式的多目标进化算法较为罕见。

本文将非线性预测控制算法中的预测误差作为偏好多目标优化的对象并将动态参考区域和移动参考点两种引导形式结合起来，提出了一种新的混合引导方式。该算法利用混合引导方式增加非劣解的选择压力，同时也保证了偏好区域的范围。另外，本文利用g-dominance［9］概念实现全局最优粒子的选取，实现对整个粒子群的有效引导，获得了最佳的控制效果。Matlab仿真结果表明本文所提改进的算法控制效果是令人满意的。

1 基本原理和问题

1.1 非线性预测控制的原理

非线性数学模型可描述为

式中：f(⋅)为非线性函数；na，nb为系统输入和输出的阶次；d为非线性系统时滞，一般令d=0。

目标函数为

1.2 多目标问题

一般多目标问题可描述如下：

式中：X 为R 空间的决策变量；gi（x），hj（x）分别为约束不等式和约束等式。

多目标问题常采用Pareto解集作为寻优的结果，目前已推出了多种改进算法。

1.3 g-dominace概念

g-dominace是由Molina J提出的一种划分目标空间，实现偏好方向引导的方法［9］。本文采用g-dominace 实现全局最优粒子的选择，其具体定义如下。

已知2 个点w 和w*∈Rm，只要满足以下2 个条件之一就可以称为点wg支配w*：

1）Flagg（w）>Flagg（w*）；

2）wi≤wi*，∀i=1，2，…，m，满足

Flagg（w）=Flagg（w*）

至少存在1个j使得wj＜wj*。

Flagv（w）定义：

式中：v为目标空间上的参考点；w为目标空间的任意一点。

2 多目标优化的MOPSO-NPC

2.1 基于多目标优化的预测控制目标函数

使用常规的预测控制算法实现对多变量系统控制时，都是通过保证目标函数中的预测误差最小，将目标函数作为单目标进行优化从而获取最优控制值。但多变量系统内部存在严重耦合时，目标函数中的各个输出变量的预测误差相互干扰，因此，其预测误差很难保证同时最小。这样，根据系统控制需求，设定不同输出变量的预测误差的范围，从而可确定各个输出变量预测误差的偏好区域。为此，本文将偏好多目标优化的思想引入到了非线性预测控制优化求解过程中。

2.2 参考区域的设计

目前，虽然基于偏好信息的多目标进化算法已经取得了巨大进步，但是当种群靠近Pareto 前沿时，增加选择压力并同时控制偏好区域和偏好范围等问题仍需进一步深入研究。为此，本文提出了混合引导的思想：设置参考点为参考区的中心并同时从初始点开始移动。当参考点到达Pareto 前沿时，参考区动态减小为一个最小区域，该范围内的非支配解就是最优解。因此，本文提出的混合动态引导的方法实现了偏好方向的准确引导同时完成了对偏好范围的控制，解决了某些算法非支配解容易收敛到一点的问题［9-10］。

2.3 参考区域及引导方程

为了获得一个可动态调整大小的参考区域，本文将参考区域设计成一个超立方体，具体表达式为

式中：s 为解空间的任意一点；c 为区域中心点；dp为超立方体半径，即超立方体中心到超立方体一个面的距离；m为目标维数。

根据式（5）可知，在种群初始时，应该设置超立方体半径为一个较大值，这样可以容纳更多的粒子。超立方体半径dp大小可依据各个粒子的适应度以及参考点位置来计算。

混合引导策略涉及参考点和参考区2 个公式。其中，参考区大小主要取决于超立方体半径变化，因此，超立方体半径dp可以代表参考区的变化。具体公式如下。

1）移动参考点表达式

式中：gen为当前次数；genmx为总运行次数；repgen为参考点；ASgen为外部档案中的非劣解。

2）超立方体半径dp表达式：

式中：dmax，dmin分别为超立方体半径的上、下限值。

2.4 混合引导过程

下面仅以两目标为例说明本文提出的混合引导策略的执行过程。混合引导策略过程如图1所示。在算法初始化时，将参考点设置为正方形中心并确定正方形的dmax和dmin值。根据式（6）和式（7）可知，当移动参考点的同时，动态减小超正方形半径，从而造成粒子选择压力的增加。当算法运行到最大次数时，参考点也正好到达Pareto 前沿上，此时，dp取最小值。每次算法循环时，都要在正方形区域内选取进入外部档案的非支配解。当dp取最小值时，档案内的非劣解即为所求。

图1 混合引导策略过程Fig.1 Process of hybrid guided strategy

图1 中实线正方形为算法初始和停止时参考区域形状，虚线正方形是算法运行时若干个过渡形状。因此，控制dp下限值就可以控制偏好范围。

2.5 全局最优粒子的选择

本文利用粒子群算法实现动态混合引导策略，并采用档案保存历史最优解，并从外部档案中随机选取全局最优粒子，引导整个粒子种群向偏好区域飞行。

为了保证全局最优粒子向偏好方向飞行，本文采用了g-dominance概念。g-dominance的优点之一就是算法的有效收敛性与参考点是否在可行域无关。g-dominance可以将档案集进行划分，flag1的区域是全局最优粒子选取的范围，具体可见图2和图3。

图2 不可行域内g-dominance图Fig.2 The g-dominance diagram in infeasible region

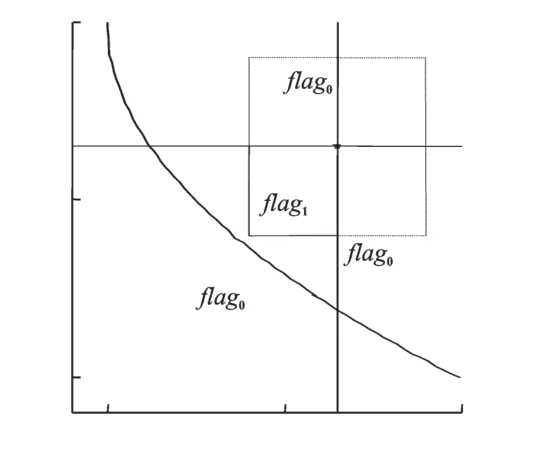
图3 可行域内g-dominance图Fig.3 The g-dominance diagram in feasible region

另外，还应注意到参考点设置在Pareto 前沿上的情况。如果这时还要移动参考点，可能造成偏好信息丢失。为了保证偏好区域的准确，将不再移动参考点，可以将参考点作为粒子群全局最优的粒子，引导种群飞行。

3 算法流程

据此，本文提出的MOPSO-NPC 算法的流程如下。

Step1：初始化。对预测控制和粒子群主要参数赋值，例如：设置预测域长度Np和预测控制域长度Nu；迭代次数gen=0，最大迭代次数genmx，超立方体半径下限dmin等。根据多目标优化的目标个数m，随机产生种群数量为N的初始种群，设定档案大小n。

Step2：判断参考点是否设置在Pareto 前沿上。如果是，令position=1，否则position=0。

Step3：计算各个粒子的多目标适应度值。

Step4：获取满足式（5）的粒子，利用Pareto支配选择档案粒子。当外部档案中非劣解超过规定数量时，采用拥挤距离方法进行维护。

Step5：当position=1时，选择参考点为全局最优粒子；当position=0 时，利用g-dominance 策略划分档案中的非劣解，随机选择全局最优值；利用支配关系选择个体最优值。

Step6：如果position=0 时，参考点更新。否则，不更新。

Step7：超立方体的d更新。

Step8：粒子群粒子更新。

Step9：gen=gen+1，如果迭代次数小于最大迭代设定值转到step 3，否则结束循环。

4 性能分析

本文选取ZDT［11］的主要测试函数来验证本文提出混合引导策略的性能。本文将MOPSO-NPC 算法中的混合引导策略和比较典型的g-dominance 算法进行了性能比较和分析，其中，将NSGA-Ⅱ算法融入到g-dominance算法中。相关仿真的基本参数设置为：种群大小为100，档案大小为100，变量维数为30，交叉概率为0.99，变异概率为0.1，最大运行次数为200。c1=c2=2，w=0.5。ZDT1，ZDT2，ZDT3，ZDT4测试函数各独立运行25次。

4.1 收敛性和分布性测试情况

本文利用GD 和SP 作为衡量算法收敛性和分布性能的指标［12-13］。GD 和SP 值越小，表明算法解的收敛性、分布性越好。测试函数ZDT1～ZDT4的参考点设置为（0.5，0.5），本文提出的混合引导策略与g-dominance 算法的GD 和SP的均值如表1所示。

通过上述性能分析，本文提出的混合偏好引导策略的收敛性指标和分布性指标均接近或超过g-dominance 算法。因此，本文的偏好引导策略具有较好的收敛性和分布性。

表1 GD和SP结果Tab.1 Result of GD and SP

4.2 参考点位置和dmin变化的影响。

当混合引导算法的参数发生变化时，选择不同的测试函数进行仿真。利用ZTD1函数进行测试时，参数dmin=0.035，参考点起始位置（0.7，0.6），测试结果如图4 所示。从图4 中可知，参考点位于可行域。

图4 dmin=0.035，ZTD1测试情况Fig.4 Preferred solution with dmin=0.035 on ZDT1

当参考点起始位置为（0.35，0.35），dmin=0.05，参考点位于不可行域，采用ZTD2函数测试，结果如图5所示。

图5 dmin=0.05时，ZTD2测试效果图Fig.5 Preferred solution with dmin=0.05 on ZDT2

利用测试函数ZTD3检测不连续空间性能，参考点位置为（0.55，0.35），dmin=0.2，测试效果如图6所示。

图6 dmin=0.2，ZTD3测试情况Fig.6 Preferred solution with dmin=0.2 on ZDT3

为了测试参考点设置Pareto前沿上或附近时的算法性能，参考点为（0.5，0.4），dmin=0.015，ZTD4测试的效果如图7所示。

图7 dmin=0.015，ZTD4测试情况Fig.7 Preferred solution with dmin=0.015 on ZTD4

根据以上测试结果可知，当参考点位置无论处于可行域或不可行域，处于Pareto 前沿上或远离前沿，算法都可以得到设定范围内的非劣解。当改变dmin值时，算法可以控制偏好范围，获得希望的最优解集。

5 实例分析

本文以连铸过程中的多变量结晶器系统作为被控对象进行分析，系统组成如图8 所示。具体参数详见文献［14］和文献［15］。

图8 结晶器系统结构图Fig.8 Structure chart of mould system

为了说明系统控制效果，分别采用SOPSO-NPC 和MOPSO-NPC 进行仿真。预测步长Np=6，预测控制步长Nu=3。仿真分为3种情况：1）设定拉速从vr=1.4 m/min 阶跃到vr=1.6 m/min，结晶器液面保持为H=50 mm；2）系统稳定后设定结晶器液面从H=50 mm 上升到H=60 mm（t ≥10）。3）拉速和液面同时发生变化。设定拉速从vr=1.4 m/min 阶跃到vr=1.6 m/min，结晶器液面从H=50 mm上升到H=60 mm。

图9 偏好解目标空间情况Fig.9 Objective space of preferred solution

图10 结晶器出口温度输出Fig.10 Temperature at the mould exit

图11 结晶器液位输出Fig.11 Output of the mould liquid level system

图9 为偏好解空间分布情况图，其中，obj1为结晶器出口铜板温度预测误差的平方和，obj2 为结晶器液位预测误差的平方和。根据结晶器控制的需要选取相应点的非劣解进行仿真，仿真结果如图10 和图11 所示。其中，图10 为结晶器出口铜板温度输出曲线，图11为结晶器液位输出曲线。从图10 中可知，结晶器拉速上升时，系统的温度输出增加3°C 左右。SOPSO-NPC 和本文改进的MOPSO-NPC 都能实现温度调节，但是MOPSO-NPC 算法的输出超调适中、响应较快。根据图11仿真情况可知，液位设定从50 mm提高到60 mm 时，运用本文所提算法，获得了较好的控制效果，没有较大震荡和超调从而说明了该算法的有效性。

另外，当拉速稳定在1.6 m/min，时间为10 s时，结晶器液位发生阶跃，SOPSO-NPC 算法的温度输出发生了0.4°C 的震荡，说明温度控制受到了液位控制的耦合影响，但本文设计算法输出比较正常，没有较大波动。同理，在图11 中液位输出受到拉速的耦合影响，基于SOPSO-NPC 算法的液位输出发生了波动。本文设计算法可以较好跟踪设定值，效果良好。

针对第3 种仿真情况，结晶器液位和出口温度的仿真结果如图12和图13所示。当液位和拉速同时变化时，由于两者之间的耦合作用，SOPSO-NPC 算法的液位和出口温度都出现了超调和震荡，控制性能降低；本文提出的算法控制结果比较稳定，在两者同时调整时没有出现较大的震荡，说明本文算法完全可以消除系统内部的强耦合影响。

图12 设定值同时变化时，结晶器液位输出Fig.12 Output of the mould liquid level system with set value changed at sme time

图13 设定值同时变化时，结晶器出口温度情况Fig.13 Temperature at the mould exit with set value changed at sme time

另外，在仿真过程中，需要合理选择有关系统系数。例如，迭代次数设置过小会造成较大的粒子选择压力，迭代次数过大又会使算法运行时间增加，影响系统响应速度。根据仿真研究的结果，迭代次数可设定50～200次较为合适；对于超立方体半径下限的设定，目前没有统一的标准和公式，但可视具体情况从［0.001～0.5］范围选择合适的值；对于预测步长和控制步长而言，一般仿真步数越多仿真结果越精确，但同时也会增加系统计算负担。当本文选择预测步长超过6，控制步长超过3 时，发现控制效果并没有明显增加。为此，本文设定预测步长Np=6，预测控制步长Nu=3。

6 结论

综上分析可知，本文对非线性预测控制算法采用了多目标优化的思想并提出了基于偏好信息的新动态引导策略，提高了非线性预测的多目标滚动优化的性能。将该算法应用到结晶器系统中，仿真结果表明运行效果良好，满足了控制需求。

［1］ 席裕庚，李德伟，林姝.模型预测控制现状与挑战［J］.自动化学报，2013，39（3）：222-236.

［2］ 焦巍，刘光斌.非线性模型预测控制的智能算法综述［J］.系统仿真学报，2008，20（24）：6581-6586.

［3］ 关圣涛，楚纪正，邵帅.粒子群优化算法在非线性模型预测控制中的研究应用［J］.北京化工大学学报，2007，34（6）：653-656.

［4］ Deb K，Pratap A，Agarwal S，et al.A Fast and Elitist Multiobjective Genetic Algorithm：NSGA-II［J］.IEEE Trans.on Evolutionary Computation，2002，6（2）：182-197.

［5］ Knowles J D，Corne D W.Approximating the Non-dominated Front Using the Pareto Archived Evolution Strategy［J］.Evolutionary Computation，2000，8（2）：149-172.

［6］ Zitzler E，Laumanns M，Thiele L.SPEA2：Improving the Strength Pareto Evolutionary Algorithm［M］.Technical Report，TIK-Report 103.Lausanne，Switzerland：Swiss Federal Institute of Technology，2001.

［7］ Reyes-sierram，Coellocac.Multi-objective Particle Swarm Optimizers：a Survey of the State-of-the-art［J］.International Journal of Computational Intelligence Research，2006，2（3）：287-308.

［8］ Coello C，Carlos A.Handling Preferences in Evolutionary Multi-objective Optimization：A Survey［C］//Proc of the Congress on Evolutionary Computation.La Jolla，USA，2000，I：30-37.

［9］ Molina J，Santana L V，Coello C A C，et al.g-dominance：Reference Point Based Dominance for Multi-objective Metaheuristics［J］.European Journal of Operational Research，2009，197（2）：685-692.

［10］余进，何正友，钱清泉.基于偏好信息的多目标微粒群优化算法研究［J］.控制与决策，2009，24（1）：66-70.

［11］Zitzler E，Deb K，Thiele L.Comparison of Multi-objective Evolutionary Algorithms：Empirical Results［J］.Evolutionary Computation，2000，8（2）：173-195.

［12］Van Veldhuizen D A，Lamont G B.Evolutionary Computation and Convergence to a Pareto Front［C］//Proc of the Late Breaking Papers at the Genetic Programming Conference.California：Stanford University，1998：221-228.

［13］Schott J R.Fault Tolerant Design Using Single and Multi Criteria Genetic Algorithm Optimization［D］.Massachusetts：Cambridge University，1995.

［14］乔国林，童朝南，孙一康.结晶器多变量耦合系统的自抗扰控制［J］.控制理论与应用，2007，24（3）：24-27.

［15］李壮举，王允建，肖磊.连铸结晶器多变量系统建模及控制［J］.中南大学学报：自然科学版，2011，42（5）：1361-1368.