基于小波-强跟踪滤波的陀螺漂移在线预测*

张 伟， 杜党波， 胡昌华， 周志杰， 张建勋

(1.第二炮兵工程大学信息工程系 西安，710025) (2.第二炮兵工程大学控制工程系 西安，710025)



基于小波-强跟踪滤波的陀螺漂移在线预测*

张 伟1， 杜党波2， 胡昌华2， 周志杰2， 张建勋2

(1.第二炮兵工程大学信息工程系 西安，710025) (2.第二炮兵工程大学控制工程系 西安，710025)

为进一步提高陀螺漂移预测精度，根据陀螺一次项漂移系数非平稳时间序列的特点，针对其数据的突变和趋势相较强的问题，提出一种基于小波和多重次优渐消因子强跟踪滤波相结合的非平稳时间序列在线预测方法，并将其应用于陀螺一次项漂移系数预测。实验结果表明，该方法能有效改善数据突变和较强趋势项所带来的状态估计不准、进而造成预测不准的问题，提高了预测精度。

小波分析； 强跟踪滤波； 陀螺漂移； 多重次优渐消因子

引言

陀螺仪是构成惯导系统的核心元件，陀螺漂移是影响陀螺精度的主要因素。如何有效提高陀螺仪的性能、抑制陀螺仪的漂移成为提高惯导系统精度的关键。陀螺漂移主要表现在漂移系数的变化，其漂移一次项系数测试数据属于趋势项较强的非平稳时间序列，能够反映陀螺漂移的程度。因此，通过预测陀螺漂移一次项系数来预测陀螺仪性能对于陀螺仪使用、维护和延长使用寿命等具有重要意义。

现有方法处理非平稳时间序列预测问题一般分为两类：基于人工智能的方法和将非平稳时间序列转化为平稳时间序列问题处理的方法。其中，神经网络等人工智能的方法[1-2]建模和预测精度较高，但在线能力相对较弱。文献[3]将非平稳时间按序列转化为平稳时间序列的方法对于含有突变等特点的复杂非平稳时间序列预测能力较弱。文献[4]将灰色预测与自回归滑动平均模型 (autoregressive moving average，简称ARMA)结合起来，针对陀螺退化进行了建模预测，指出采用混合方法比单一方法的预测精度高。文献[5]针对陀螺漂移预测比较了卡尔曼滤波和小波分析分别与ARMA结合起来预测的优缺点。文献[6]采用小波和ARMA组合的方法对粮食产量进行了预测，但在线能力较弱。Zheng等[7]提出的小波和卡尔曼滤波相结合的方法(wavelet-Kalman filtering hybrid estimating and forecasting algorithm，简称WKHEFA)是将小波分析的多尺度特性、在时域和频域均具有多分辨率分析的特点和卡尔曼滤波的实时性、递归性和易实现等特点结合起来的预测方法，对于负荷等周期性较强的数据有较好的预测能力，但当非平稳时间序列周期性不明显，且含有突变和较强趋势项等特点时会表现出模型建立不准、预测精度不高的问题。文献[8]加入了带单重次优渐消因子的强跟踪滤波，仿真验证了其有效性，但其单通道的强跟踪特性对于陀螺漂移一次项系数等工程实例仍有放大误差的不足，不能达到预期的预测结果。

笔者针对陀螺仪一次项漂移系数具有较强趋势项和突变的特点，结合强跟踪滤波对于突变状态的强跟踪特性，在小波和卡尔曼滤波混合预测方法的基础上进行了改进，将小波分解和强跟踪滤波算法中多重次优渐消因子的思想相结合，提出一种同时具有实时性、递归性、多通道强跟踪性和多尺度分析特性的在线预测方法，并对陀螺仪漂移一次项系数进行了预测。实验结果表明，该方法有效改善了数据突变和较强趋势项突变所带来的状态估计不准，进而造成预测不准的问题，提高了预测精度。

1 问题描述

对于某一非平稳时间序列数据

z(t)=s(t)+v(t)

(1)

其中：s(t)为非随机部分；v(t)为随机干扰项。

s(t)中经常含有趋势项、季节项即周期项等，WKHEFA方法对周期性强的非平稳时间序列进行离散小波变换,使小波系数构成的新序列具有随机游走特性。该方法将小波和卡尔曼滤波结合起来，对具有周期性的负荷数据有较好的预测结果，但对于含有突变和趋势项较强的非平稳时间序列数据采用该方法并不能很好的进行预测，主要问题：a. WKHEFA方法所建模型不能很好地匹配含有突变或趋势项较强的非平稳时间序列，即模型建立不准，从而导致卡尔曼滤波出现预测不准确或者发散的情况；b. WKHEFA方法在预测具有周期性特点的数据时，周期是已知或易于得到的，即小波分析所选数据段长度是易于得到的，而对于周期性不强的数据，小波分析所选的数据段长度难以把握。

针对第1个问题，笔者采用带多重次优渐消因子的强跟踪滤波代替卡尔曼滤波进行预测并在数据段内进行状态更新。陀螺漂移系数等非平稳时间序列发生突变时，其各系统状态分量即小波系数的突变程度是不同的，需采用具有多通道强跟踪能力的带多重次优渐消因子强跟踪滤波对系统状态进行跟踪。虽然和采用单重次优渐消因子相比，在一定程度上提高了算法的复杂度，但对于抑制采用单重次优渐消因子引起的非突变通道的误差有很好的效果，同时仍然能够改善模型建立不准所带来的状态估计值偏离系统状态的现象。针对第2个问题，笔者在其他条件不变、所选数据段长度不同的情况下进行了实例验证，得出了陀螺一次项漂移系数预测时应选取的数据段长度。最后对涉及算法的实时性进行了对比分析。

2 带多重次优渐消因子的小波-强跟踪滤波的非平稳时间序列在线预测

提出的带多重次优渐消因子的小波-强跟踪滤波的非平稳时间序列在线预测方法的整个算法流程如图1所示。其中：Hi为小波重构矩阵的第i行；l为数据段长度；Z(m)为第m个观测值；m=k·l+i-1。从图1可以看出，该算法主要包括3步：a.小波分析信号分解，建立系统模型；b.强跟踪滤波在线更新的一步状态预测；c.利用小波重构矩阵对状态进行重构，得到预测结果。

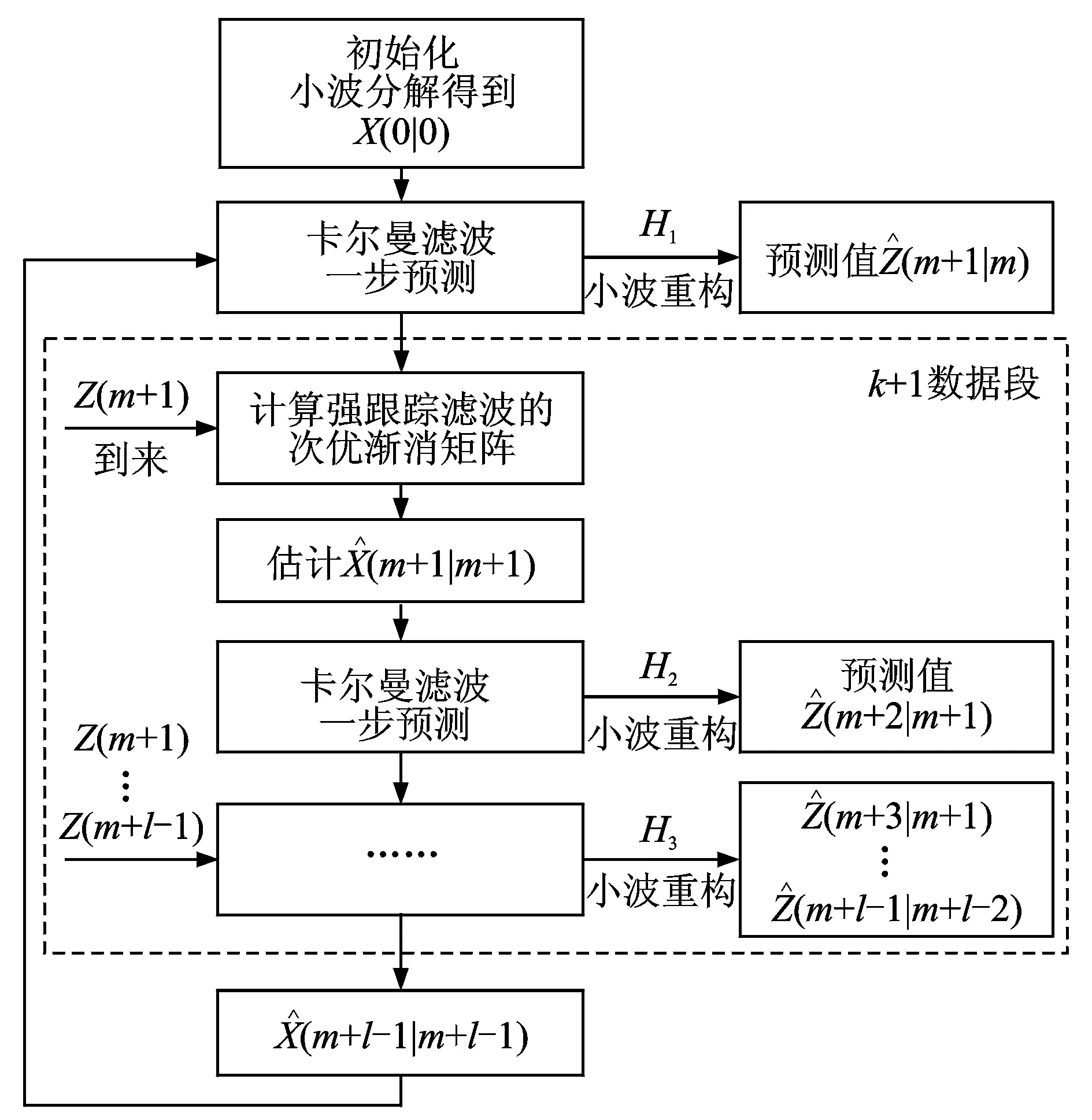
图1 预测算法流程图Fig.1 Flow chart of the prediction method

2.1 基于小波分析的信号分解

设{Vj}j∈Z为L2(R)的一个多分辨分析，φ(x)为{Vj}中的尺度函数。φ(x)为{Vj}中的正交尺度函数，在最细尺度M上，z(t)，s(t)，v(t)在选定长度的数据段内[7]可分别表示为

(2)

对s(t)进行离散小波变换,带入式(2)可得

(3)

对式(3)两端同时与φM,r(t)做内积，有

(4)

式(4)可整理为

z(r)=HrWs+v(r)

(5)

其中:Hr为小波重构矩阵的第r行[9]；Ws为小波系数；r=1,2,…,2M。

把整个所选数据段各个时刻的采样值写成向量形式，并假设将小波系数看作状态变量，则将z(k)描述为状态方程形式

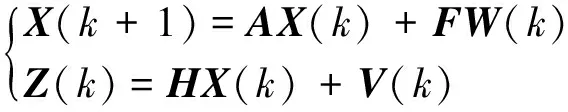
(6)

其中：A，F为l×l的单位阵；H为l×l的观测阵即小波重构矩阵；k表示数据段的序号；X(k)为l维状态变量即小波系数。

W，V分别为l维系统和观测噪声，并假设其满足以下统计特性

(7)

其中：Q(k)为对称非负定阵；R(k)为对称正定阵。

2.2 强跟踪滤波算法

强跟踪滤波(strong tracking filter，简称STF)的代表算法是引入次优渐消因子进行强跟踪[10-11]，描述的系统中状态变量是小波系数。文献[8]中强跟踪滤波采用的是单重次优渐消因子对其进行强跟踪，但小波系数是由一个逼近系数和其他细节系数构成。当趋势项较强的测量数据发生突变时，主要是逼近系数发生了突变，所以为了实现对小波逼近系数的强跟踪，弱化其他系数对预测造成的影响，不适宜采用带单重次优渐消因子的卡尔曼滤波(suboptimal fading Kalman filter, 简称SFKF)，而应采用带多重次优渐消因子的卡尔曼滤波(suboptimal multiple fading Kalman filter,简称SMFKF)[12]进行强跟踪。

多重次优渐消因子主要思想是：采用多个次优渐消因子分别对不同的数据通道(状态分量)进行渐消，为了进一步提高滤波器的跟踪能力，通过引入渐消记忆矩阵L(m+1)实时调整状态预报误差的协方差阵以及增益来实现。当由先验知识得到状态X(m+1)的某分量Xi(m+1)易于突变时，可相应增大与其对应的次优渐消因子的比例系数，这样有助于实现对此分量的快速跟踪。

P(m+1|m)=L(m+1)AP(m|m)AT+FQFT

(8)

X(m+1)可由下面的方法[12]计算得到

(9)

V0(m+1)=

(10)

N(m+1)=V0(m+1)-

Hi+1(m)FQFTHi+1(m)T-βRi+1(m)

(11)

M(m+1)=Hi+1(m)AP(m|m)ATHi+1(m)T

(12)

(13)

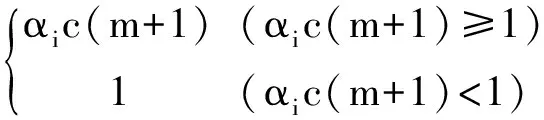
(14)

L(m+1)=

(15)

其中：λi(m+1)=αic(m+1),i=1,2,…,l；β≥1为选定的弱化因子，可以避免过调节，β可以由经验得到，也可以仿真得到；0<ρ≤1为遗忘因子，一般取ρ=0.95。

2.3 带多重次优渐消因子的小波-强跟踪滤波在线预测算法

带多重次优渐消因子的小波-强跟踪滤波在线预测算法(suboptimal multiple fading-wavelet-Kalman filtering hybrid estimating and forecasting algorithm，简称SM-WKHEFA)是将强跟踪滤波和小波分解结合起来，利用小波分解得出的数据多尺度特征，将分解出的小波系数作为状态变量，同时利用强跟踪滤波进行实时多通道强跟踪和动态预测的一种同时具有递归性、实时性、多通道强跟踪性和多尺度分析特性的方法。

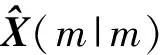
(16)

(17)

其中：Hi(m)为观测矩阵即小波重构矩阵第i行。

(18)

(19)

(20)

(21)

令m=m+1，重复以上运算即可实现对每个测量值的一步预报。

综合以上思想，总结整个SM-WKHEFA算法步骤如下。

1) 初始化，计算X(0|0)，给定l，Q,R,P(0|0)，状态分量权值和所选用小波。由小波重构矩阵计算X(0|0)=H×Z(0)。给定数据段长度l=2n，n为小波分解层数。

(22)

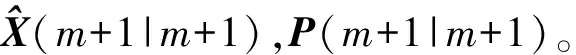
4) 令m=m+1，返回步骤2，可实现一步预测。

这里n的选取根据不同数据的特点取值不同，本研究由实验方法得到。

3 实例验证

3.1 问题描述

笔者采用某型号单自由度液浮陀螺仪一次项漂移系数作为实例验证，如图2所示。陀螺漂移一次项系数测量序列具有较强趋势项且存在几个明显的跳变，且数据周期特性并不明显。针对此问题，首先，采用SM-WKHEFA对陀螺仪一次项漂移系数进行预测；然后，讨论此算法针对陀螺一次项漂移系数应选取的数据段长度；最后，分别将改进前后的算法用于陀螺一次项漂移系数预测进行对比，得出结论。

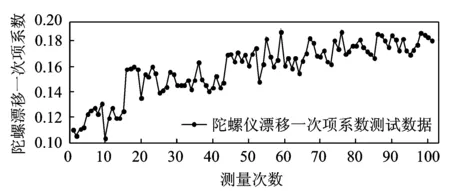
图2 陀螺仪一次项漂移系数曲线Fig.2 Graph of gyro drift 1-order coefficient

3.2 在线预测

如图3所示，采用SM-WKHEFA对陀螺仪一次项漂移系数进行在线预测。由于Haar小波结构简单，便于计算，是小波分析中最早用到的具有紧支撑的正交小波函数，故这里选取Haar小波为例。选取n=2，Q=1×10-10×Il×l，R=1×10-9×Il×l，l=2n=4，P=1×10-6×Il×l，λ1(m+1)∶…∶λn(m+1)=α1∶…∶αn=100∶1∶…∶1。

图3 SM-WKHEFA在线预测结果Fig.3 Predict results of online SM-WKHFA

为评价预测结果，引入评价指标。绝对误差均值为

(23)

其中：L为数据总长度。

误差标准差为

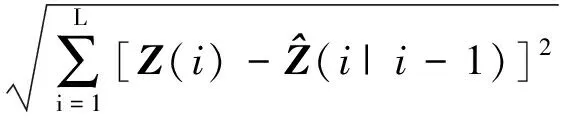
(24)

从图3(b)中可得到MAE=0.804 4×10-2，SDE=1.039 0×10-2。可见，所提算法能够较好地对陀螺仪一次项漂移系数进行预测，并在原数据发生突变时能较快跟踪并进行预测。

3.3 数据段长度的选取

在SM-WKHEFA中，n表示进行小波分解的层数，l=2n表示所选数据段的长度。当n较大时，小波分解可以提取更纯净的趋势项，但也有可能去掉有用信息，同时强跟踪滤波在进行预测时由于间隔长度过长会导致精度下降。当n较小时，强跟踪滤波进行预测各数据段长度比较短，相邻数据段之间变化较小，但此时小波分解并不能很好地分解出较为纯净的趋势项，也会影响建模精度。可见，n的选取很重要，根据不同数据，n的选取也会不同。针对陀螺仪漂移系数数据，分别选取n为不同值进行建模预测，对比结果如表1所示。可以看出，当n=1,2时，预测结果相差不大；但当n>2时，预测误差明显增大。同时，由于小波分解在层数相对较多的情况下分离趋势项的作用和抑制高频干扰均较好，故对陀螺仪一次项漂移系数进行预测时取n=2，即每一数据段长度为l=2n=4。

表1 SM-WKHEFA选取不同n时预测误差比较

3.4 改进前后方法比较

为进一步检验本研究方法的有效性，将改进前后的方法用于陀螺一次项漂移系数，比较其预测结果。选取基本WKHEFA方法、WKHEFA方法[7]、带单重次优渐消因子的小波-强跟踪滤波预测方法(suboptimal fading-wavelet-Kalman filtering hybrid estimating and forecasting algorithm，简称SF-WKHEFA)[8]以及笔者所提的SM-WKHEFA方法分别对陀螺仪一次项漂移系数进行一步预测。其中，基本WKHEFA方法是指不进行一步更新的方法，后3种方法都是一步更新预测。针对在线预测算法对实时性的要求，对以上方法的计算时间进行统计，如表2所示。所有方法的数据长度l=2n=4，初始值选取相同，运行环境为windows xp，Intel core (TM) 2 Duo CPU T6570 双核，2 GB内存。

如图4，5为所得结果，基本WKHEFA没有一步更新，其他3种是一步更新后的结果。可见，WKHEFA预测结果明显好于基本WKHEFA预测，这是因为加入新信息的更新，使得状态较未更新之前有所改善；SF-WKHEFA预测结果并没有WKHEFA预测结果好，这是因为强跟踪在更新状态时，单重次优渐消因子对除小波逼近系数以外的细节系数影响也进行了放大，而细节系数是高频部分，多含有噪声，不能很好地跟踪结果，进而不能很好地预测；笔者采取的SM-WKHEFA预测方法得到的结果相比于WKHEFA预测结果能够较好地对原数据进行预测，且当数据发生较大变化即突变时能够很好地进行跟踪，保证了其后数据预测的精度，这也验证了笔者采用多重次优渐消因子而不采用单重次优渐消因子的分析正确。

由表2可知，SM-WKHEFA预测方法在预测绝对误差均值和误差标准差时能有效提高精度，验证了本研究方法的有效性。在线能力方面，虽然几种方法的实验用时随着算法复杂度的增加而增加，但都不超过0.1 s，且在线能力和预测精度两者互相矛盾，在相同数量级的用时下，可以根据测试要求选择更合适的算法。陀螺仪漂移系数标定需要6位置测试才能完成，远远大于算法计算所需要的时间，因此本研究算法能够达到在线能力的要求。

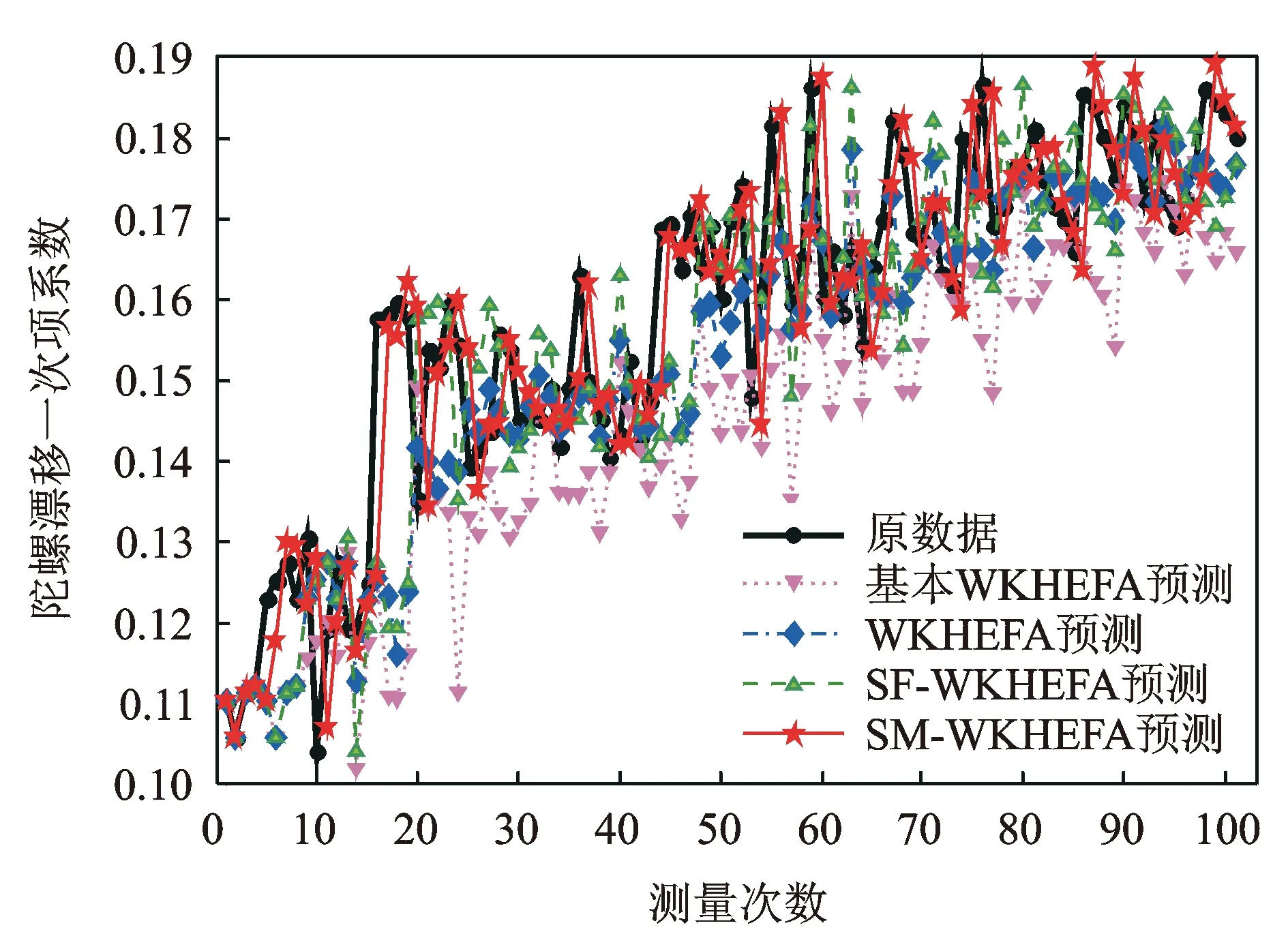
图4 改进前后预测方法结果比较Fig.4 Predict results comparison of the improved and original algorithm

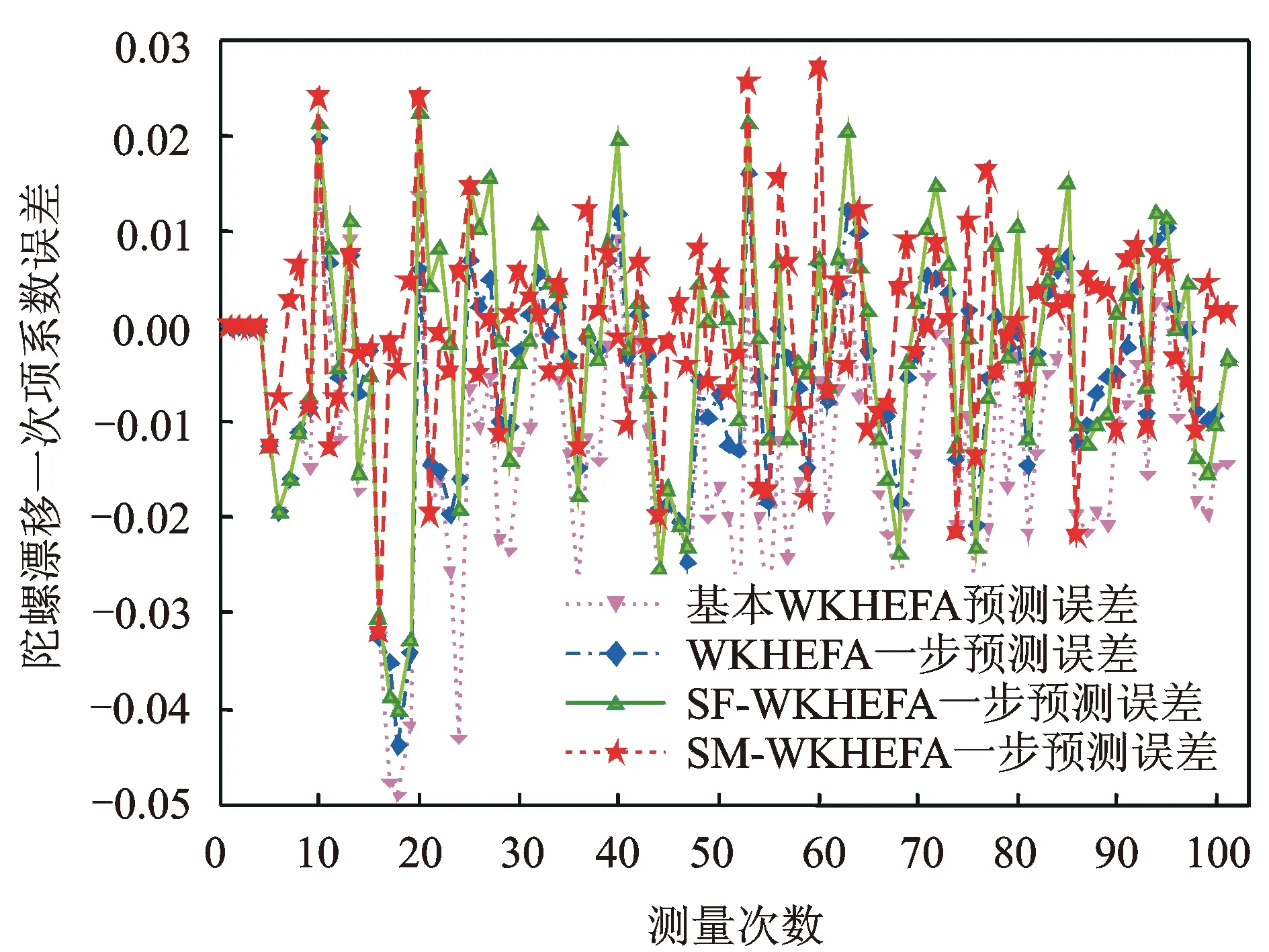
图5 改进前后预测方法误差比较Fig.5 Predict error comparison of the improved and original algorithm

表2 改进前后预测方法误差比较

研究模型是建立在小波系数的随机游走性质前提下的[7]，状态转移矩阵A为单位阵，而强跟踪滤波在多步预测时只是简单的用状态转移矩阵进行迭代，多步预测结果效果较差。因此当需要进行多步预测时，可考虑对状态转移矩阵进行改进，使其能够反映状态之间的关系。

4 结束语

结合具有较强趋势项非平稳性时间序列数据的特点，将多重次优渐消因子强跟踪滤波引入小波-卡尔曼滤波预测方法中，提出一种同时具有递归性、实时性、多通道强跟踪性和多尺度分析特性的小波和强跟踪滤波在线预测方法，并针对陀螺仪一次项漂移系数进行分析预测。实验证明，SM-WKHEFA能有效抑制陀螺漂移系数建模不准的缺陷，增强了对数据突变的跟踪能力，使得预测结果与传统小波-卡尔曼滤波方法相比, 绝对误差均值和误差标准差都更小，提高了预测精度。但是，SM-WKHEFA只是缓解了模型建立不准带来的缺陷，在进行多步预测时预测精度会降低，所以对所建模型进行改进，提高建模精度是下一步研究的重点。

[1] 黄晓冬,朱四华.小波神经网络在陀螺漂移预测中的应用[J].兵工自动化,2012, 31(2)：82-84.

Huang Xiaodong, Zhu Sihua. Application of wavelet neural network on gyro drift prediction[J]. Ordnance Industry Automation, 2012,31(2)：82-84. (in Chinese)

[2] 李方溪,陈桂明,朱露,等.基于经验模态分解与RBF神经网络的混合预测[J].振动、测试与诊断,2012,32(5)：817-822.

Li Fangxi, Chen Guiming, Zhu Lu, et al. Hybrid prediction method based on empirical mode decomposition and RBF neural network[J]. Journal of Vibration, Measurement & Diagnosis, 2012,32(5)：817-822. (in Chinese)

[3] 单伟,何群.基于非线性时间序列的预测模型检验与优化的研究[J].电子学报,2008,36(12):2485-2489.

Shan Wei, He Qun. Research of the optimizing and testing of forecasting model based on the non-linear time series[J]. Acta Electronica Sinica, 2008,36(12):2485-2489. (in Chinese)

[4] Zhou Zhijie, Hu Changhua. An effective hybrid approach based on grey and ARMA for forecasting gyro drift[J]. Chaos, Solitons and Fractals, 2008,35(3):525-529.

[5] 周志杰,胡昌华,韩晓霞.基于非平稳时间序列的陀螺漂移性能建模与预测方法研究[J].电光与控制,2005,12(3):23-26.

Zhou Zhijie, Hu Changhua, Han Xiaoxia. Study on the methods for modeling and forecasting gyro′s drift performance based on non-stationary time series[J]. Electronics Optics & Control, 2005,12(3):23-26. (in Chinese)

[6] 谷政,褚保金,江惠坤.非平稳时间序列分析的WAVELET-ARMA组合方法及其应用[J].系统工程,2010,28(1):73-77.

Gu Zheng, Chu Baojin, Jiang Huikun. WAVELET-ARMA method in the non-stationary time series and its application[J]. Systems Engineering, 2010,28(1):73-77. (in Chinese)

[7] Zheng Tongxin, Girgis A A, Makram E B. A hybrid wavelet-Kalman filter method for load forecasting[J]. Electric Power Systems Research, 2000,54(1):11-17.

[8] 余利文.强跟踪滤波与小波分析理论在短期电力载荷预测中的应用研究[D].杭州:杭州电子科技大学,2009.

[9] Hu Zhikun, Xu Fei, Gui Weihua, et al. Wavelet matrix transform for time-series similarity measurement[J]. Journal of Central South University of Technology, 2009,16(5):802-806.

[10]胡昌华,张琪,乔玉坤.强跟踪粒子滤波算法及其在故障预报中的应用[J].自动化学报,2008,12(34):522-528.

Hu Changhua, Zhang Qi, Qiao Yukun. A strong tracking particle filter with application to fault prediction[J]. Acta Automatica Sinica, 2008,12(34): 522-528. (in Chinese)

[11]陈业,胡昌华,周志杰,等.一种改进的SR-CDKF算法及其在早期微小故障检测中的应用[J].自动化学报, 2012,38(9):1063-1074.

Chen Ye, Hu Changhua, Zhou Zhijie, et al. Method of improving square-root center difference kalman filter with application to incipient failure detection[J]. Acta Automatica Sinica, 2012,38(9):1063-1074. (in Chinese)

[12]周东华,席裕庚,张钟俊.一种带多重次优渐消因子的扩展卡尔曼滤波器[J].自动化学报,1991,17(6):689-695.

Zhou Donghua, Xi Yugeng, Zhang Zhongjun. A suboptimal multiple fading extended kalman filter[J]. Acta Automatica Sinica, 1991,17(6):689-695. (in Chinese)

*国家杰出青年科学基金资助项目(61025014)；国家自然科学青年基金资助项目(61004069)；陕西省自然科学基金资助项目(2011JQ8007)

2013-01-24；

2013-03-31

10.16450/j.cnki.issn.1004-6801.2015.01.013

TP273 ; TN713 ; V241.5; TH17

张伟，女，1966年4月生，博士、副教授。主要研究方向为故障诊断与预测、智能计算。 E-mail：zhang1966wei@163.com