地震多点反应谱模型存在缺陷的改进与验证*

柳国环， 练继建， 国 巍， 耿 辰， 田 利

(1.天津大学水利工程仿真与安全国家重点实验室 天津，300072) (2.天津大学建筑工程学院 天津，300072)(3.中南大学土木工程学院 长沙，410075) (4.天津城建大学土木工程学院 天津，300384)(5.山东大学水利与建筑工程学院 济南，250100)



地震多点反应谱模型存在缺陷的改进与验证*

柳国环1，2， 练继建1，2， 国 巍3， 耿 辰4， 田 利5

(1.天津大学水利工程仿真与安全国家重点实验室 天津，300072) (2.天津大学建筑工程学院 天津，300072)(3.中南大学土木工程学院 长沙，410075) (4.天津城建大学土木工程学院 天津，300384)(5.山东大学水利与建筑工程学院 济南，250100)

推导出基于位移和位移-速度输入模型的多点反应谱。阐述了基于位移输入模型所导出反应谱的缺陷及其逻辑必然性，说明了基于加速度模型导出的多点反应谱计算结果有效的偶然性、必然性及其适用范围，并给出数值算例予以验证。分析表明：基于位移-速度导出的多点反应谱理论严格；基于位移输入模型导出的多点反应谱会导致底部单元内力不收敛，计算结果不合理；基于加速度输入模型导出的多点反应谱结果虽然有效，但适用于经典阻尼体系，在推导过程中的忽略项在理论上具有误差相互抵消的特点。

地震地面运动； 多点反应谱； 加速度输入模型； 位移-输入模型； 位移-速度输入模型； 经典阻尼

引言

当前，地震动多点输入下的结构反应分析已成为抗震工程界研究热点之一，位移输入计算模型备受青睐。在频域内，根据随机振动理论可以推导出多点响应谱(multi-support response spectrum，简称MSRS)法理论表达式，与时程分析方法相比，该方法计算快、简单实用，可方便用于工程结构设计。

国内外学者在MSRS法方面进行了诸多研究。Alejandro等[1]针对地震激励下的二次结构在多支撑输入下进行了反应谱分析。Berrah等[2]利用修正系数对反应谱值进行修正来考虑地震动多点激励的空间变化效应，并利用一致激励情形时组合方法求解结构最大响应。Kiureghian等[3]采用随机振动理论推导出具有较严格意义的MSRS法，考虑了行波效应、部分相干和局部场地效应影响、地面运动的相关性以及各振型之间的相关性。Loh等[4]针对MSRS计算量大的缺点，给出了积分系数求解简化的计算方法。王君杰[5]推导出一般阻尼结构体系在多维多点地震动作用下的结构响应MSRS法。刘先明等[6]对拟静力反应项与动力反应项进行了研究并予以简化，减少了计算量。

目前，MSRS法是基于位移-速度输入模型基础上忽略两项阻尼的加速度输入模型而推导出的，包括由Kiureghian提出的目前相对最为严密的MSRS法。值得一提的是，Wilson[7]提到：采用数学模型分析可能得到与实际物理模型行为有较大差异的计算结果，并作了相关说明。这里所谈及到的数学模型即为加速度输入模型。近年来，位移输入模型被广泛采用，笔者也强调了位移输入模型的优势与缺陷[8]，陆续作了系统性相关介绍。基于文献[7]，笔者在后续工作中详细分析了位移输入模型存在的问题[9]，并提出了理论严格的无质量刚性元(appended massless constraint element，简称AMCE)实效对策。为了便于结构工程师解决实际工程问题，进一步提出了无质量刚性元法[10]，该方法已经应用于一实际桥梁工程计算[11]。相比之下，位移-速度模型保留了速度项，相关内容参见文献[9-10]。

与位移-速度模型相比，加速度输入模型忽略了两项阻尼，位移输入模型忽略了一项阻尼，导致了基于该模型得到的MSRS表达式有所不同。鉴于此，笔者说明了当前基于“加速度输入模型”导出的MSRS模型的“偶然性”和“必然性”，指出基于位移输入模型导出MSRS的不合理及其逻辑必然性，阐述了有必要基于“位移-速度输入模型”导出MSRS的逻辑性和必要性，并给出理论公式。最后，结合算例进行了验证与说明。

1 时域输入模型本质区别

1.1 时域模型公式推导及其区别

一离散单元的结构体系与地面刚性连接，将其自由度分为两类：n个非支座节点自由度与m个支座节点自由度。地震地面运动作用下，该体系的动力平衡方程[1]可表达为

(1)

(2)

式(2)即为位移-速度输入模型。将结构非支座节点的绝对位移分为两部分表达

X=Xd+Xs

(3)

(4)

其中：R为影响矩阵。

(5)

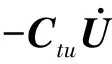
(6)

表1为3种不同计算模型或等价模型右端项对比与说明。同时，基于不同计算模型导出的多点反应谱在表中也给出了名称，便于描述方便。

表1 3种不同计算模型或等价模型右端项对比与说明

Tab.1 Comparision among the right-hand items of three different calculation models or equivalent models

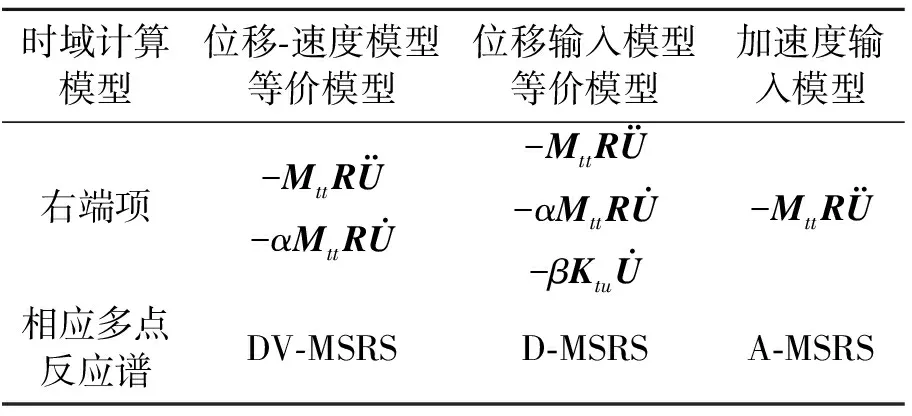
时域计算模型位移⁃速度模型等价模型位移输入模型等价模型加速度输入模型右端项相应多点反应谱

1.2 基于不同输入模型的多点反应谱

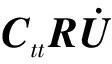
相比之下，基于位移-速度输入模型导出的MSRS，即DV-MSRS逻辑上理论最为严格，因为位移-速度输入模型本身不涉及到忽略项。鉴于此，笔者推导出基于位移-速度输入模型的DV-MSRS和基于位移输入模型的D-MSRS，并指出其不收敛的问题。

2 基于位移-速度与位移时域模型的结构反应表达式

2.1 基于位移-速度模型的结构反应表达式

基于文献[3]，根据式(2)推导结构时域反应计算公式。式(1)中，当不考虑惯性力与阻尼项时，有下式成立

KttXs+KtuU=0

(7)

(8)

其中：Xs为拟静力反应。

结构绝对反应X可表达为动反应Xd与Xs之和，即

X=Xd+Xs

(9)

将式(7)，(8)代入式(2)，得到

(10)

(11)

令

R=[r1…rk…rm]T

(12)

(13)

其中：rk为R的第k列向量；ik为m维单位矩阵的第k列向量。

将式(12)，(13)代入式(11)，得到

(14)

其中：U=[u1(t)…uk(t)…um(t)]T。

令

yi=yiα+yiβ

(15)

则

(16)

(17)

(18)

(19)

分别比较式(16)，(18)和式(17)，(19)，得到

(20)

(21)

因此，可得到广义坐标为

(22)

根据有限元知识，结构反应可表达为

(23)

其中：系数ak，bki和cki分别表示为ak=ΗTrk(k=1,…,m)；bki=ΗTφiαki(k=1,…,m;i=1,…,n);cki=ΗTφiβki(k=1,…,m;i=1,…,n);Η为反应转换向量。

2.2 基于位移和加速度模型的结构反应表达式

(24)

(25)

3 基于时域模型的多点反应谱

根据随机振动理论及文献[3]，有下式成立

(26)

(27)

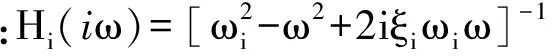
对式(26)两边在ω∈(-∞,+∞)上进行积分，得到结构反应方差的表达式为

(28)

(29)

(30)

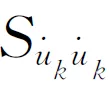
表2 3种形式多点反应谱对比

Tab.2 Comparision among the three multiple-supported response spectrum

多点反应谱名称DV⁃MSRSD⁃MSRSA⁃MSRS谱表达式Sr(ω)Sdr(ω)Sar(ω)分析比较没有省略任何项表达形式同Sr(ω)，但cdki≠cki表达形式同Sr(ω)，但caki=0

4 算例验证

4.1 算例与相关参数

如图1所示，算例模型包括构件(切向刚度表示为K1和K3，轴向弹簧刚度表示为K2)、节点(上部节点和支座节点)以及相关参数表示。方便起见，只考虑水平x向平动有效自由度。

图1 算例模型示意图Fig.1 Model sketch of numerical example

反应向量为

(31)

(32)

(33)

相应的刚度和质量矩阵分别为

(34)

(35)

(36)

(37)

(38)

(39)

(40)

通过模态分析，得到两个振型的广义模态质量以及相应的振型向量为

(41)

(42)

(43)

根据两个振型的圆频率ω1=25.334rad/s和ω2=25.338rad/s以及振型阻尼比ξ1=ξ2=0.02，得到瑞利阻尼的质量阻尼系数α=0.507和刚度阻尼系数β=7.89×10-4。计算式(11)中的Ctt和Ctu，根据式(13)得到由αki和βki组成的系数矩阵A和B为

式(26),(27)中传递函数Hj(iω)由模态圆频和阻尼比也可求出。

4.2 DV-MSRS验证及其与D-MSRS和A-MSRS对比

图2为分别采用位移-速度输入模型对文中算例进行时程计算结果(HHT积分方法)。可以看出：采用位移-速度输入模型，不同n值底部单元剪力(底部剪力)基本重合，而采用位移输入模型则计算结果不同且差异较大，说明了当前被广泛采用的位移输入模型存在底部单元内力随单元逐步划分不稳定且不收敛的问题，从而说明了文献[9-10]强调的问题不容忽视。

图3为位移-输入模型与加速度输入模型的剪力对比与相对误差(n=100)，说明结果比较相近。

表3为以位移-速度输入模型的直接积分时程法(以此计算结果为标准)，DV-MSRS，D-MSRS和A-MSRS计算得到的反应方差，并给出误差分析。可以看出，由DV-MSRS计算的误差为5.41%(n=10)和5.28%(n=100)。这不仅说明了笔者所改进的模型结果的有效性和精确性，也说明了DV-MSRS计算结果的稳定性。相比之下，采用D-MSRS计算结果的误差为9.08%(n=10)和1 368%(n=100)，进一步说明了D-MSRS的不可靠性和不稳定性，这在理论上具有逻辑必然性。采用A-MSRS计算结果的误差为7.13%(n=10)和6.67%(n=100)，说明对于经典阻尼体系，A-MSRS与DV-MSRS计算结果的相近性。

表3 采用不同方法计算底部单元剪力的方差与误差分析

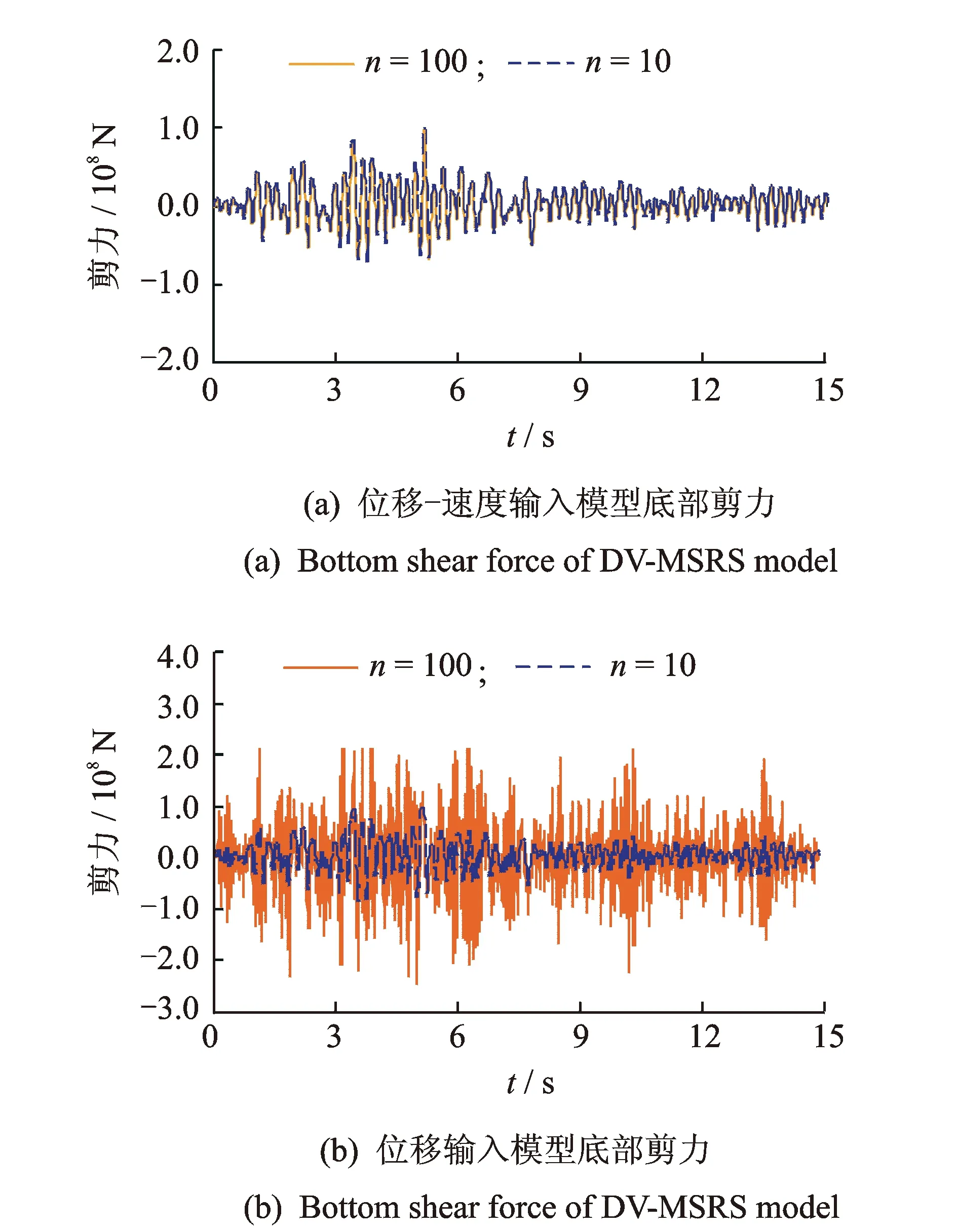
图2 不同计算模型不同工况底部单元剪力时程Fig.2 Shear force history of different cases using different analysis model

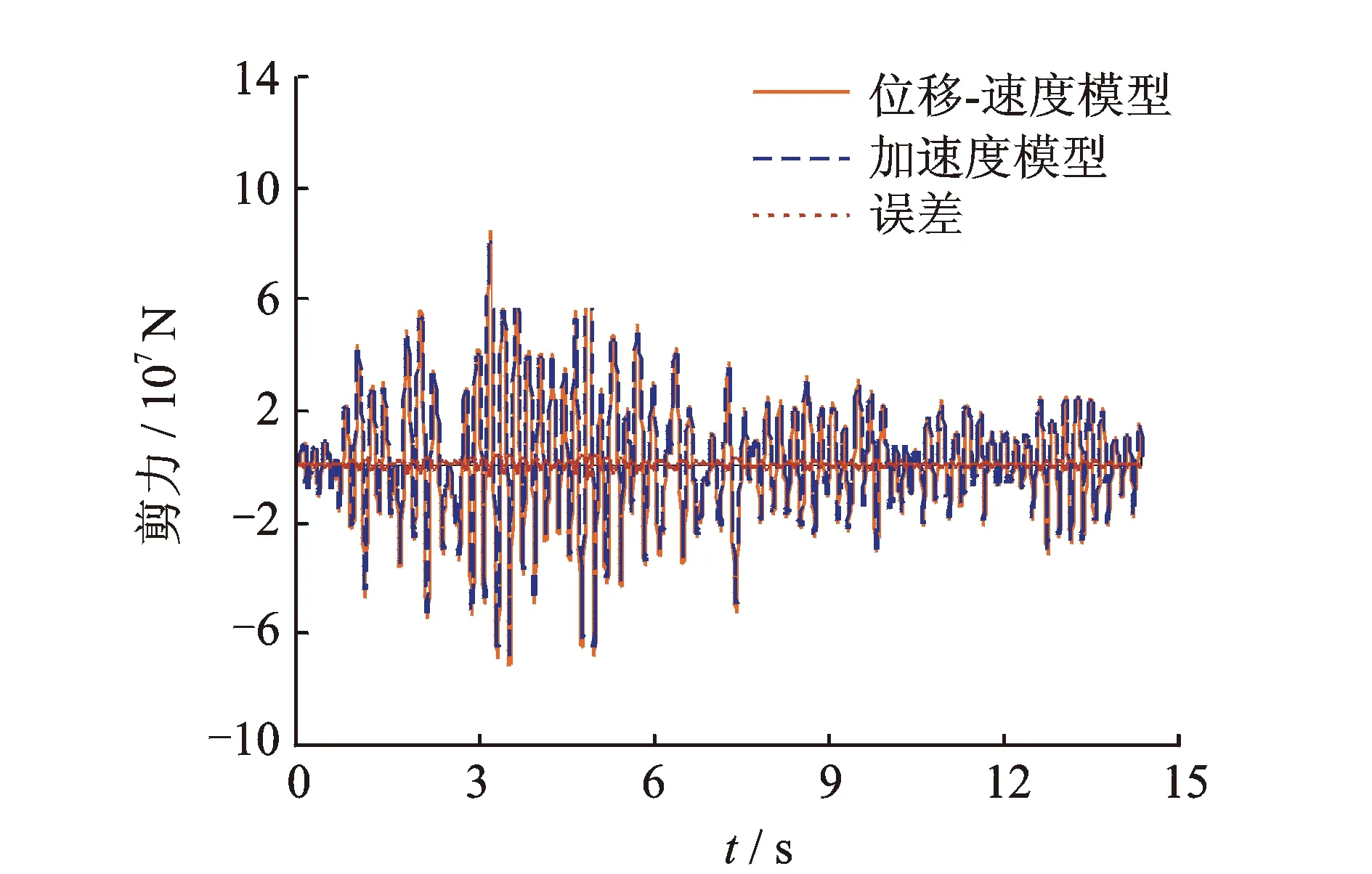
图3 位移-速度与加速度底部单元剪力比较Fig.3 Comparision of shear force between displacement-velocity and acceleration model

5 结 论

1) 说明A-MSRS计算结果的有效性，客观认识A-MSRS，指出了在理论上严格的适用范围为经典阻尼结构体系。

2) 指出D-MSRS所导致问题(底部单元内力随单元精细划分而不收敛)的逻辑必然性，分析其根本原因，并通过算例验证。

3) 推导出DV-MSRS，并通过算例验证了计算结果的有效性和稳定性。对于非经典阻尼结构体系，指出了DV-MSRS与A-MSRS之间的差别及其不容忽视性。

[1] Alejandro A, Kiureghian A D. Floor response spectrum method for seismic analysis of multiply supported secondary systems[J]. Earthquake Engineering & Structural Dynamics, 1985,14(2): 245-265.

[2] Berrah M, Kausel E. Response spectrum analysis of structures subjected to spatially varying motions[J]. Earthquake Engineering & Structural Dynamics, 1992, 21(6): 461-470.

[3] Kiureghian A D, Neuenhofer A. Response spectrum method for multi-support seismic excitations[J]. Earthquake Engineering & Structural Dynamics, 1992,21(8): 713-740.

[4] Loh C H, Ku B D. An efficient analysis of structural response for multiple-support seismic excitations[J]. Engineering Structures, 1995,17(1): 15-26.

[5] 王君杰. 多点多维地震动随机模型及结构的反应谱分析[D]. 哈尔滨：国家地震局工程力学研究所，1992.

[6] 刘先明，叶继红，李爱群. 多点输入反应谱法的理论研究[J]. 土木工程学报，2005，38(3)：17-22.

Liu Xianming, Ye Jihong, Li Aiqun. Research of multi-support response spectrum method[J]. China Civil Engineering Journal, 2005, 38(3): 17-22. (in Chinese)

[7] Wilson E L. Three-dimensional static and dynamic analysis of structures: A physical approach with em-

phasis on earthquake engineering[M]. California: Computers and Structures Inc, 2004：167-169.

[8] 柳国环,李宏男,林海.结构地震响应计算模型的比较与分析[J].工程力学, 2009，26(2)：10-15.

Liu Guohuan, Li Hongnan, Lin Hai. Model comparision and analysis for structural seismic response[J]. Engineering Mechanics，2009，26(2)：10-15 (in Chinese)

[9] 柳国环,李宏男,国巍.求解结构地震响应位移输入模型存在的问题及其AMCE实效对策[J]. 计算力学学报，2009，26(6)：862-869.

Liu Guohuan , Li Hongnan, Guo Wei. Existing problem of displacement input model for calculating structural responses under earthquake ground motion and its an actual effective solution method called AMCE[J]. Chinese Journal of Computational Mechanics, 2009，26(6)：862-869.(in Chinese)

[10]柳国环,李宏男,国巍,等.求解结构地震响应位移输入模型中存在问题的一种新解决方法[J]. 工程力学, 2010, 27(9): 55-62.

Liu Guohuan, Li Hongnan, Guo Wei, et al. A new method for solving existing problem of current displacementinput model for calculating structural seismic responses[J]. Engineering Mechanics, 2010, 27(9): 55-62.(in Chinese)

[11]柳国环,李宏男,田利.九江长江大桥在多点多维地震激励下的反应分析[J]. 振动与冲击, 2009,28(9):204-209.

Liu Guohuan, Li Hongnan, Tian Li. Response analysis of Jiujiang Yangze River highway bridge under spatially variable earthquake ground motions[J]. Journal of Vibration and Shock, 2009,28(9): 204-209.(in Chinese)

*国家自然科学基金青年基金资助项目(51408409)；中国博士后科学基金资助项目(2011M500332)

2013-07-16；

2013-09-16

10.16450/j.cnki.issn.1004-6801.2015.01.005

P315.9; U442

柳国环，男，1980年6月生，博士、副教授。主要研究方向为工程结构动力计算。曾发表《求解结构地震响应位移输入模型中存在问题的一种新解决方法》(《工程力学》2010年第27卷第9期)等论文。

E-mail：liugh@tju.edu.cn