基于射影几何的CCD相机几何模型研究

孙 瑜,李占利

(西安科技大学计算机科学与技术学院,西安710054)

基于射影几何的CCD相机几何模型研究

孙 瑜,李占利

(西安科技大学计算机科学与技术学院,西安710054)

为提高由多幅二维图像解算出的空间坐标信息的精度,基于射影几何原理,提出一种像方空间与物方空间的几何形状计算方法。分析电荷耦合器件(CCD)相机成像射影几何原理,根据透视变换和交比不变性质,利用直线之间存在平行、垂直和相交等关系,建立基于直线特征的相机成像几何模型,已知相机参数,证明并推导像方空间二维影像和物方空间形状与坐标信息的几何转换关系。分析结果表明,该方法结合了整幅图像的几何信息,能提高空间点等几何特征的坐标信息计算精度,以及视觉测量和三维重建的精度。

电荷耦合器件相机;射影几何;透视变换;交比;成像模型

1 概述

根据在不同视点上所获取的二维影像来重建原空间物体的三维模型是摄影测量以及计算机视觉等领域的热门研究内容。由二维图像到三维重建,它们之间的变换关系由摄像机成像几何模型决定［1-3］。相机成像几何模型是进行三维重建数据处理的基础,主要描述相机像方空间与物方空间坐标变换关系［4-6］。文献［7-8］分别进行了空间圆精确定位与检测的研究与探讨。关于相机镜头畸变的问题,文献［9］根据交比不变性原理利用拟合函数计算相机畸变参数,文献［10］用非线性优化方法实现了镜头畸变参数的标定,文献［11］利用共轭节面的性质建立了一种图像畸变几何模型,提出了图像畸变的解决方法。本文研究电荷耦合器件(Charge Coupled Device,CCD)相机成像几何模型,分析相机成像几何原理,建立相机成像几何模型,根据相机参数推导计算像方空间边界轮廓与物方空间边界轮廓的透视对应关系。

2 相机成像原理

典型的CCD相机模型是基于共线原理的,物体空间中的每个点经过一条过投影中心的直线投射到图像平面［12-13］。用摄像机去拍摄物体,得到拍摄物体的图像,空间物体与图像中物体的对应关系是射影几何中的中心投影,也称为透视投影［14］。如图1所示,这时透视中心就是摄影中心S,即相机的光学中心。光轴为SSi,透视轴是图像平面A′B′C′D′与物体平面ABCD的交线l。为不失一般性,假设像平面与物体平面夹角为α。下面进一步研究像平面与物平面的透视对应关系。

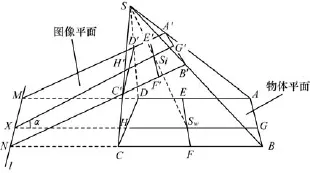
图1 相机成像几何模型

3 像方空间与物方空间的对应关系

3.1 图像平面信息

拍摄一幅图像,它的形状为矩形,且已知它的长和宽。设图像平面矩形为A′B′C′D′,长为2a,宽为2b。在图2中,Si为图像中心,从Si向透视轴l做垂线,垂足为X。

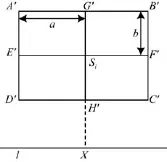
图2 图像大小

在图像平面上已知A′B′=C′D′=E′F′=2a,A′D′=B′C′=G′H′=2b,Si是矩形A′B′C′D′的中心,所以,G′Si=SiH′=b,E′Si=SiF′=a。

3.2 成像几何关系推导

建立过光轴、垂直于透视轴的平面几何关系如图3所示。已知摄像机光学中心为S,摄像机焦距为f,则SSi=f,光轴上光学中心到物体平面的距离为d,d=SSw,图像平面与物体平面的夹角为α,∠SiXSw=∠SwSI=∠SiSI′=α,摄像机俯仰角为θ,∠SiSH′=∠SiSG′=θ;tanθ=b/f。,cosθ=。

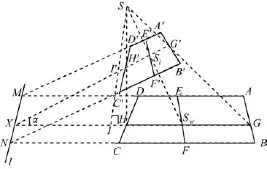
图3 成像几何关系

如图3所示,从摄影中心向物方平面作垂线,作SI⊥GX,交G′X于点I′。在RtΔSSiI′中,易知:

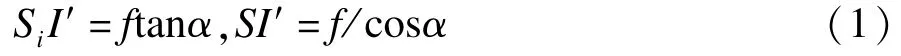
在RtΔSISw中,可以推导得到:

由式(1)、式(2),可以推导出:

在RtΔXSiSw中,可以推导得:

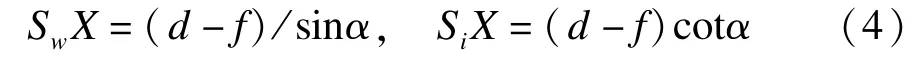
在RtΔSiSH′中,可知tanθ=b/f,θ=arctan(b/f),推导得到:

在RtΔSIG中,由于∠GSI=α+θ,结合式(2),推导得到:

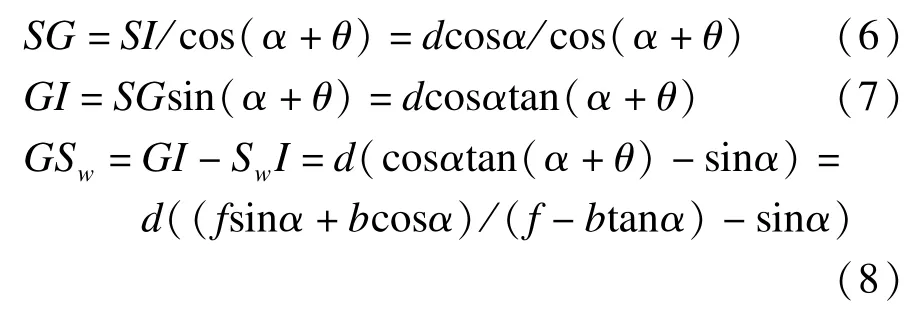
4 物方边界形状分析与证明

下面讨论经摄像可得到矩形图像的空间几何形状特征。

讨论平行于透视轴的直线变化规律。已知相机焦距为f,视点沿光轴到物体所在平面的距离为d,则SSi=f,SSw=d。透视变换具有如下透视性质:平行于透视轴的一组平行弦,透视后仍然平行于透视轴。

建立过光轴、平行于透视轴的平面几何关系,即物方几何关系如图4所示。

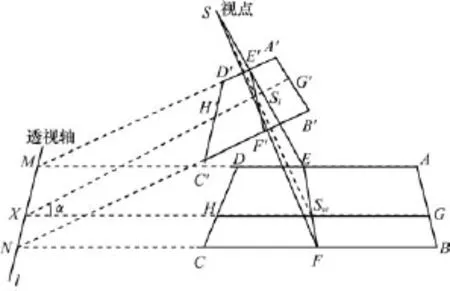
图4 物方几何关系

根据透视性质,由于光轴垂直于图像平面,有SSi⊥E′F′,因为E′F′//l,所以EF//l。

物方边界轮廓分析如图5所示,在 ΔESF和ΔE′SF′中,可以推导得到下式:

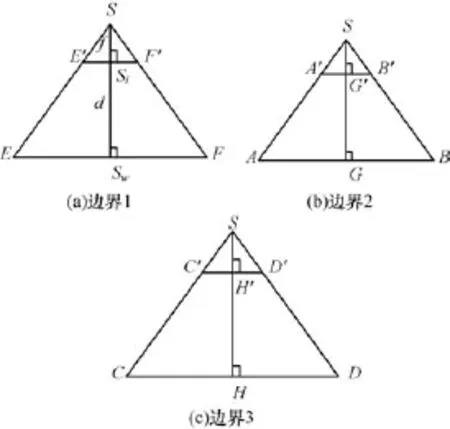
图5 物方边界轮廓分析

如图5(a)所示,结合式(9),可知E′F′/EF=f/ d,因此:

同理在图 4中,由于边A′B′//l,AB//l,因此AB//l,CD//l,因此AB//CD。

如图5(b)所示,在ΔSAB中有:BG=GA。

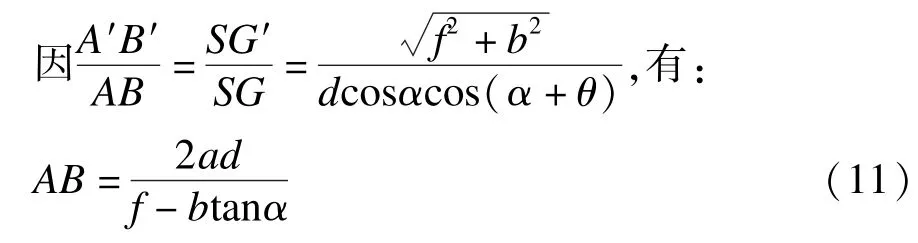
如图5(c)所示,在ΔSCD中有:DH=HC。

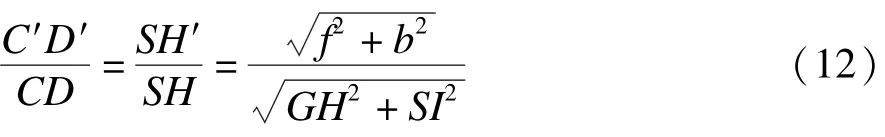
综合以上结论,然后分析物方空间轮廓形状。如图6所示,因为l⊥ΔSSwX,所以GH⊥l,GH⊥AB,且GH平分上下底,得证四边形ABCD是等腰梯形。因此,得到看出,图像平面的矩形A′B′C′D′是与物方平面上的等腰梯形ABCD透视对应的。

图6 物方边界轮廓

从以上分析可知,图像平面的矩形是与物方空间的等腰梯形透视对应的,这也说明了一个现象,平行于透视轴的2条等长线段,距离眼睛远的那条看起来比距离近的这条长度要短。

5 透视对应轮廓大小的确定

在射影几何中,中心投影具有如下性质:

性质 射影变换保持点的共线及交比不变。

也就是说,若A,B,C,D4个点共线,则经射影变换后,其对应的像点Ac,Bc,Cc,Dc仍然共线,且交比保持不变,即cross(A,B;C,D)=cross(Ac,Bc;Cc,Dc)。

根据以上性质,讨论共面线束SG,SSw,SH,SX的交比,可以转化为计算G′X和GX上4点的交比,即:

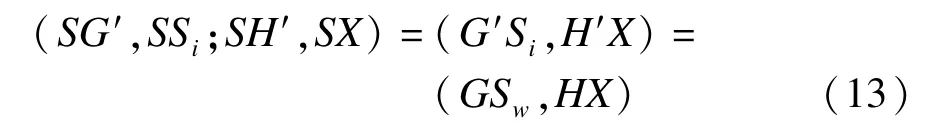
结合式(4),将式(13)推导如下:

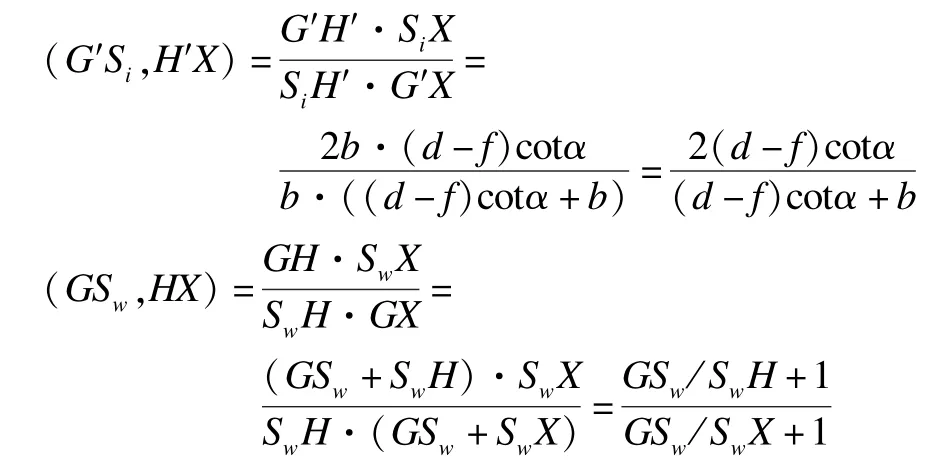
根据上面(GSw,HX)计算公式,结合式(8),可以求出SwH,有:

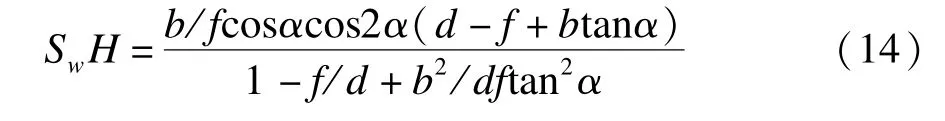
进而可以根据HX=SwX-SwH,计算得出HX。

至此,可以利用式(2)、式(14),将式(12)化简,得到:

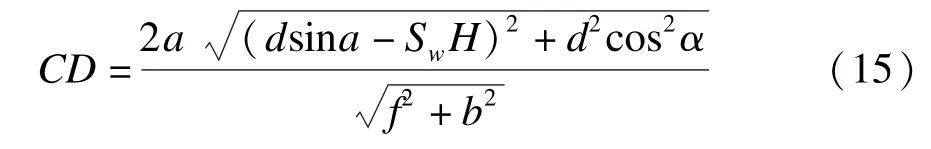
如图6所示,根据影像的矩形大小,计算推导出了透视对应的空间梯形大小,包括梯形的上下底、高以及投影中心在梯形的位置。

综合以上分析与推导,可以得到以下结论:

(1)矩形图像是与等腰梯形透视对应的,透视轴平行于等腰梯形的底,靠近透视轴的底小,较远的底大。

(2)给定矩形图像的大小、相机焦距、相机与物体平面夹角与距离,可以计算出透视对应的等腰梯形的位置与大小。

(3)矩形图像上被图像中心平分、垂直于透视轴的线段,在空间平面中,它的透视对应线段是垂直于透视轴的,但图像中心透视对应点比该线段中点离透视轴方向更近些。

6 结束语

本文研究基于射影几何的CCD相机几何模型。通过对相机成像模型与轮廓透视对应关系的讨论,针对针孔相机的透视对应特点,基于射影几何的透视变换性质,推导物方空间的形状、位置与大小。分析结果表明该模型为准确表达二维图像与空间物体的透视关系提供理论依据,可用于三维重建的像方空间与物方空间坐标转换,具有一定理论意义和工程应用价值。今后将对相机畸变的实际问题做进一步研究。

［1］冯文灏,李建松,闫 利.基于二维直接线性变换的数字相机畸变模型的建立［J］.武汉大学学报:信息科学版,2004,29(3):254-258.

［2］赵双明,冉晓雅,郭芯宏.CE-1立体相机成像几何模型研究［J］.测绘科学,2011,36(6):112-114.

［3］刘松林,哈长亮,郝向阳,等.基于机器视觉的线阵CCD相机成像几何模型［J］.测绘科学技术学报, 2006,23(5):387-390.

［4］Janne H,Olli S.A Four-step Camera Calibration Procedure with Implicit Image Correction［EB/OL］.(1997-11-21). http://www.vision.caltech.edu/bouguetj/calib_doc/papers/heikkila97.pdf.

［5］李竹良,赵宇明.基于单幅图片的相机完全标定［J］.计算机工程,2013,39(11):5-8.

［6］郭成玉,袁政鹏,吴家麒,等.半球幕几何校正与标定方法的研究［J］.计算机工程,2011,37(2):281-283.

［7］李占利,刘 梅,孙 瑜.摄影测量中圆形中心像点计算方法研究［J］.仪器仪表学报,2011,32(10): 2235-2241.

［8］周 封,杨 超,王晨光,等.基于随机Hough变换的复杂条件下圆检测与数目辨识［J］.仪器仪表学报, 2013,34(3):622-628.

［9］陈 辉,吕乃光.基于交比不变性的相机镜头畸变标定研究［J］.北京机械工业学院学报,2006,21(1): 1-3.

［10］方素平,夏晓华,肖 燕,等.一种线阵相机镜头畸变的标定方法［J］.西安交通大学学报,2013,47(1): 11-14.

［11］张春明,解永春,王 立,等.一种基于共轭节面的图像畸变分析方法［J］.光学学报,2012,32(11):1-7.

［12］李鸿燕,张学山.基于射影变换几何不变性的数码相机双目定位模型［J］.上海工程技术大学学报,2009, 23(4):333-337.

［13］智喜洋,张 伟,曹移明,等.单线阵CCD相机定位精度评估模型及几何误差研究［J］.光学技术,2011, 37(6):669-674.

［14］方德植,陈奕培.射影几何［M］.北京:高等教育出版社,1983.

编辑 刘 冰

Research on Geometric Model of CCD Camera Based on Projective Geometry

SUN Yu,LI Zhanli
(College of Computer Science and Technology,Xi’an University of Science and Technology,Xi’an 710054,China)

Aiming at enhancing the spatial coordinates precision solved by 2D images,a new method based on projective geometry for calculation of 3D model coordinate transformation between image side and object side space is proposed.Charge Coupled Device(CCD)camera imaging geometric principle is analyzed based on perspective transformation and cross-ratio invariant properties.Imaging geometric model based on linear feature is established using the relationship of parallel,perpendicular and intersecting between straight lines.With acquired photographs and camera parameters,the shape and size of the corresponding scene space are deduced and proved on the basis of the cross ratio invariability of collinear points with perspective projection.The coordinate transformation between image side and object side space of the 3D model is calculated.And perspective correspondence from image side to object side space is built. Experimental results prove that the calculation accuracy of the spatial points coordinates can be enhanced by image geometric information.The method can be applied to enhance the precision of image feature extraction and location of geometric features such as circle,and to increase the measurement precisiong of the photogrammetry system and 3D coordinate reconstruction.

Charge Coupled Device(CCD)camera;projective geometry;perspective transformation;cross ratio;imaging model

1000-3428(2015)05-0270-04

A

TP391.41

10.3969/j.issn.1000-3428.2015.05.050

陕西省自然科学基金资助项目“基于视觉计算的井下信息感知理论与方法研究”(2012JM8029)。

孙 瑜(1982-),女,讲师、硕士,主研方向:计算机视觉;李占利,教授、博士。

2014-04-30

2014-07-11E-mail:1224682061@qq.com

中文引用格式:孙 瑜,李占利.基于射影几何的CCD相机几何模型研究［J］.计算机工程,2015,41(5):270-273.

英文引用格式:Sun Yu,Li Zhanli.Research on Geometric Model of CCD Camera Based on Projective Geometry［J］. Computer Engineering,2015,41(5):270-273.