基于MapReduce与蚁群优化的航路规划算法

柏 硌,赵刚要

(南昌航空大学航空制造工程学院,南昌330063)

基于MapReduce与蚁群优化的航路规划算法

柏 硌,赵刚要

(南昌航空大学航空制造工程学院,南昌330063)

航路规划是提高无人机生存能力的有效途径,可使其安全、快速到达目的地。为在云计算环境中分布式并行地求解航路规划问题,应用云计算技术提出基于MapReduce和多目标蚁群算法的航路规划算法(RPMA)。设计多目标蚁群算法,并采用多种优化策略对传统算法进行改进。RPMA能预先规划出多条航迹,可根据不同的飞行任务选择不同的航路,并在飞行过程中根据不同需要临时确定合适的飞行航路。仿真实验结果表明,RPMA求解航路问题是可行、有效的,具有较好的收敛性和扩展性,以及对大规模数据的处理能力。

云计算;MapReduce分布式编程;蚁群优化;航路规划;无人机;Hadoop分布式文件系统

1 概述

无人机航路规划是在综合考虑无人机到达时间、油耗、威胁以及飞行区域等因素的前提下,为无人机规划出最优或是满意的飞行航路,以保证圆满地完成飞行任务。航路规划是提高无人机生存能力,并确保其安全、快速到达目的地的有效途径［1］。

国内外的许多专家和学者对航路规划问题进行了研究,取得了不少成果。航路规划有静态预规划［2］和动态实时规划［3］。 规划空间有二维［4］、三维［2,5］或更多维［6］。从优化方案上讲,目前大多采用将多个性能指标进行加权和的方法,形成一个单目标函数,根据单一目标函数进行寻优,如文献［2-6］。这种方案多是生成一条具有最小代价的飞行航迹,如文献［3-4,6］。然而,在实际航路规划中,无人机受环境、飞行任务和自身很多条件的约束,要建立一种能够包含所有这些因素的代价函数是很困难的,并且对航迹的评价会因具体飞行任务而改变,更增加了确定代价函数的困难。另外,环境因素会随时间发生变化,预先规划好的最优航迹在任务执行时可能不再适用,并且对于某些无人机,由于负荷限制不可能在机上进行实时航迹再规划。一种有效解决问题的途径是预先规划出多条航迹,在任务执行时根据不同需要临时决定选择合适的飞行航迹［2］。从数学意义上讲,航路规划是在多约束条件下,多目标函数的极值问题,多目标的优化方法往往能更好地求解问题。航路规划问题的搜索空间十分广阔,且随精度的高要求,计算量成指数增大,需要在分布式并行的环境中进行求解。目前,航路规划算法多运行在串行环境中,对较大规模和高精度的航路规划问题求解困难,且在分布式并行的云计算环境下对该问题的研究很少。

云计算的关键技术MapReduce［7-9］编程模式用于大规模数据集的并行运算,它简化了分布式系统的编程,用户只需提供自己的Map函数和Reduce函数即可在分布式的云平台中并行处理海量数据。蚁群算法［10-11］是一种仿生类群体智能优化算法,受启发于科学家对蚂蚁觅食模型的研究,具有高的隐含并行性。算法成功地应用于求解许多组合优化问题,如TSP、二次分配、图着色等。虽然蚁群算法在求解组合优化问题中表现突出,但也存在缺陷,如搜索时间较长,易于过早地收敛于非最优解;当问题的规模达到一定程度时,在集中式串行环境下求解效率较低。云计算和智能算法联系紧密,许多群体智能算法因具有隐含并行性,可以在云计算系统中实现分布式并行计算［11］。

本文提出基于MapReduce和多目标蚁群算法的航路规划算法(RPMA),在二维空间分布式并行地求解多目标多航路预规划问题。设计多目标蚁群算法对蚁群算法进行合理的优化和改进,有效改善了蚁群算法搜索时间长且易于收敛于局部最优解的缺陷。RPMA应用MapReduce编程模式和Hadoop分布式文件系统(Hadoop Distributed File System, HDFS)等云计算技术,使算法分布式并行地运行在开源的Hadoop云计算平台中,增强了对大规模数据的处理能力,并能得到无人机航路规划问题的多条航路。无人机可根据需要从中选择最满意的航路,其他航路将作为备选方案以备发生意外时启用。

2 航路规划问题

无人机在飞行过程中会受到自身性能限制和外部环境的威胁。本文简化了问题描述,在二维空间描述航路规划问题。将威胁区统一建模为圆形区域,表示为☉A{o(x,y),r},其中,威胁区圆心为o(xo,yo);半径为r(如图1中☉A1)。本文考虑无人机自身性能限制包括:最大航程MR和最大转向角θ。本文算法可扩展到对更多维环境和更多约束条件的航路规划问题求解。

用网格表示航路规划问题的搜索空间,表示为二维矩阵Gridm×n。无人机航路可表示为网格上的一系列导航点,设起点为S,目标点为G,相邻导航点坐标为ai(xi,yi),ai+1(xi+1,yi+1),如图1所示,记航路R为{S,a1,a2,…,an-2,G}。本文采用2个目标函数来表达航路的性能指标,即航路长度目标函数(记为L)和航路到威胁区距离目标函数(记为D)。ai到ai+1的航路长度记为Li,i+1。航路长度目标函数L的计算见式(1),其中,LS,1,Ln-2,G分别为起点S到a1的距离和an-2到目标点G的距离。

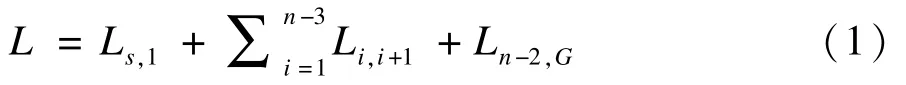
航路到威胁区距离目标函数D的计算见式(2)。

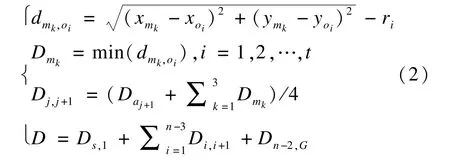
其中,DS,1,Dn-2,G分别为S到a1,an-2到G航路到威胁区距离;t为威胁区个数。

无人机航路规划问题示意图如图1所示,其中,将航路段ajaj+1四等分,等分点为m1,m2,m3;点mk(xmk,ymk)到威胁区☉Ai{o(xoi,yoi),ri}的距离为dmk,oi;点mk到威胁区距离Dmk为mk到各个威胁区距离的最小值;航路ajaj+1到威胁区距离Dj,j+1为各分点及aj+1点到威胁区距离Dmk之和的平均值。

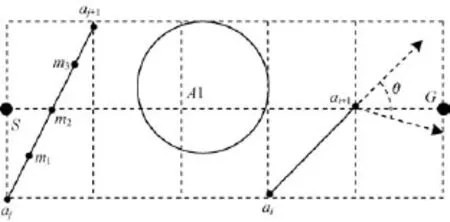
图1 无人机航路规划问题示意图

记航路aiai+1对应的向量为Vi+1=(xi+1-xi,yi+1-yi),则无人机转角的约束条件可表达为式(3)。

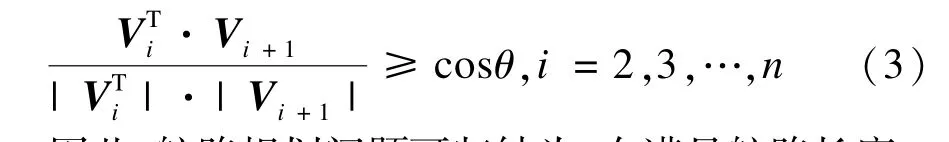
因此,航路规划问题可归结为:在满足航路长度L不大于最大航程MR、无人机转角φ不大于最大转向角θ、导航点不在威胁区3个约束条件下,航路长度L最小,航路到威胁区距离D最大,且2个目标函数都优化的多目标优化问题。其形式化描述为式(4)。

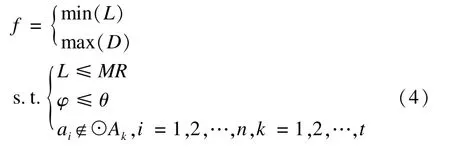
3 RPMA算法

3.1 总体描述

MapReduce包含r个Map和k个Reduce,每个Map处理一部分不同的原始数据,各个Map独立运行,可实现充分并行,Reduce对Map产生的中间结果进行再处理,且每个Reduce处理的中间结果互不交叉,所有Reduce并行执行,其产生的结果合并为完整结果集。

RPMA运行流程如图2所示。其中,将航路非劣解数据文件分割成r个数据段及r个Map结果的归并由云平台自动完成。

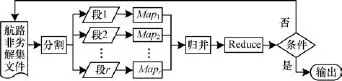
图2 RPMA执行流程

RPMA算法的描述如下:

算法 RPMA

在RPMA算法中,初始化包括初始化输入、输出文件的路径、最大迭代次数、云平台运行环境配置参数、蚁群算法相关参数等。Map阶段和Reduce阶段参见下文描述。云平台中的一个job(任务)包括2个阶段:Map和Reduce。云平台具有管道能力,可以将Reduce结果传给下一代,作为Map的输入,这样可将多个job串行起来,进行多代求解,得到航路非劣解集。

3.2 多目标蚁群算法的相关元素

蚁群算法［10-11］的主要元素有解表示、目标函数、启发函数、信息素、概率公式等。经典蚁群算法一般用于求解单目标问题,且可以收敛到最优解。对多目标的航路规划问题需要重新设计蚁群算法的相关元素。

(1)解及目标函数:每条航路R为一个解,解sol记为{S,a1,a2,…,an-2,G},存储这些导航点的xy轴坐标。每条航路对应2个目标函数:航路长度目标函数L和航路到威胁区距离目标函数D。对多目标问题,其解的优劣是相对的,不存在绝对最优,通常会有一组最优的pareto解(非劣解集)。

(2)启发函数:为了多目标寻优,本文设计航路长度和到威胁区距离2个启发函数。航路长度启发函数ηLij为航路aiaj长度的倒数,到威胁区距离启发函数ηDij为航路aiaj到威胁区距离除以该段航路长度,如式(5)所示。这样,对某段航路,其长度越长,航路长度启发函数越小,蚂蚁选择该航路的可能性越小;其到威胁区距离越小,到威胁区距离启发函数越小,蚂蚁选择该航路的可能性也越小。

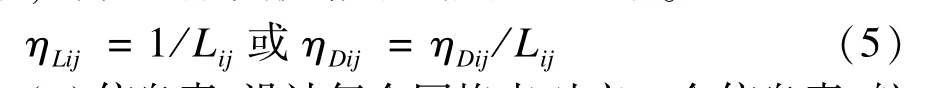
(3)信息素:设计每个网格点对应2个信息素,航路长度信息素τLij,到威胁区距离信息素τDij,且威胁区中网格点的τLij和τDij设为0。信息素更新公式如式(6)所示,ρ(0＜ρ＜1)为信息素衰减系数,△τLij, ΔτDij为增加量。更新规则为:先衰减所有信息素,再对非劣解集中包含的网格点信息素增加ΔτLij或ΔτDij。

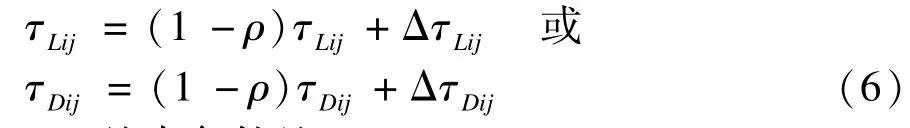
(4)约束条件处理:

1)最大航路长度MR约束:设蚂蚁已经从S点搜索到ai点,若S到ai点航路长度大于MR,则该蚂蚁放弃该求解过程。

2)最大转向角θ约束:设下一个要选择网格点为aj,ai点在网格的第i列,则aj在网格的i+1列;aj在网格的第多少行,即aj所在行的范围rows,受无人机最大转向角θ的约束,无人机只能在当前的飞行方向上顺时针或反时针最大转θ角,由式(3)可以计算出aj纵坐标的范围,再由网格点纵坐标和网格行数间的关系计算出rows。这样,第i+1列上rows行范围内的网格点集合C(C命名为蚂蚁视角范围)都满足该约束条件。aj为在集合C中选出的一个网格点。

(5)概率公式:每个网格点对应着航路长度选择概率PLij和到威胁区距离选择概率PDij,概率计算公式如式(7)所示。其中,α,β为参数,C同上,为蚂蚁视角范围。这样,第j列网格上C集合中各点的航路长度选择概率之和为1,威胁区距离选择概率之和为1,且威胁区中网格点上的概率为0。

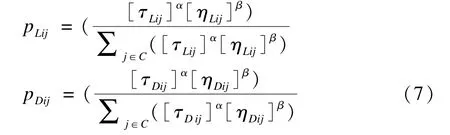
3.3 RPMA的Map函数

Map函数实现蚁群算法中蚂蚁独立构造解的过程。本文设计Map函数中有多个蚂蚁(形成一个蚂蚁分队)进行求解,因为在云平台中求解问题,平台本身要消耗一定的时间,设置多个蚂蚁求解,则Map时间(问题求解的时间)增长,问题求解时间比例增加,能提高问题求解效率。每个蚂蚁从起点S开始,沿网格行的方向,在网格的每列上选择一个导航点,最终到达目标点G,形成一条航路,即得到一个解。Map函数的形式化描述见式(8)。输入为键值对＜key1,value1＞,key1为数据段索引号,value1为上一代得到一条航路及其目标函数值;输出为多个键值对 ＜key2i,value2i＞,本文设计 key2i都为 1, value2i为该蚂蚁分队求得的航路非劣解集。

Map(key1,value1)→{＜key2i,value2i＞|

i=1,2,…,k1} (8)

Map函数描述见函数1。其中,第4步的Nant为蚂蚁分队中蚂蚁的数量;第7步,idx称为求解索引,若idx=0,则根据式(5)和式(7)计算启发函数ηLij和概率PLij,否则计算ηDij和PDij;第8步的Ngrid为搜索空间的网格列数;第9步参见3.2节约束条件处理部分;第11步蚂蚁的选点方式见3.4节算法的优化;第15步change_sc(sol,sc)见函数2;第16步～第18步将该蚂蚁分队求得的非劣解集及目标函数和索引idx作为Map产生的中间结果输出,其将作为Reduce的输入。

函数1 RPMA的Map函数

函数change_sc(sol,sc)实现多目标函数的解比较选优。功能为:将解sol和非劣解集sc中解进行比较,若sol的2个目标函数值都优于sc中的某些解,则删除sc中这些劣解,并将sol添加到sc中;若sol的目标函数值只有一个优于sc中的解,将sol添加到sc中;否则sol不能添加到sc中。

3.4 RPMA的Reduce函数

云平台会对Map函数输出的键值对结果进行排序和聚集,使相同key的结果交给一个Reduce处理。本文设计Map输出的key都为1,这样所有Map结果,形成一个解列表,都交给一个Reduce函数,并作为其输入,有利于解的比较和信息素更新。Reduce函数形式化描述为式(9),其中,key3j为索引 idx; value3j为航路非劣解及其目标函数值。

Reduce(key2,{value21,value22,…})→

{＜key3j,value3j＞|j=1,2,…,k3}(9)

Reduce函数实现了以下功能:比较各个蚂蚁分队求得的非劣解集(非劣航路),得到当前非劣航路集合,更新信息素,输出非劣航路及目标行数值。Reduce函数的描述如函数3所示。其中:第3步同Map函数中的第15步;第2步～第3步实现解比较选优,去除劣解,得到当前非劣航路集合;第4步计算解密度(见3.4节及函数4);第8步根据式(6)和解密度,对解sol中包含的导航点进行信息素增加,若求解航路时,idx=0,则τLij增加ΔτLij,若idx=1,则τDij增加ΔτDij;第10步～第12步输出当前非劣航路及其目标函数值。

函数3 RPMA的Reduce函数

3.5 RPMA的优化策略

RPMA采用了3种主要策略对常规的蚁群算法进行优化,相关表述如下:

(1)蚂蚁选点方式优化策略:蚂蚁在其视角范围C内,采用2种选点方式,按概率大者选点或按轮盘赌选点,并且这两种选点方式根据参数q(0≤q≤1)动态变化。具体实现为:生成随机数r(0≤r＜1),若r＜q,则按概率大者选点;否则按轮盘赌选点。在求解初期,由于信息素缺乏,q设置较大,按概率大者方式选点的机会较多,有利于加快问题求解速度;在求解后期,由于信息素积累,q逐渐变小,按轮盘赌选点方式较多,增加问题求解的随机性,有效改善蚁群算法易于收敛到局部优解的缺陷。

(2)优良解保持策略:设计上一代Reduce输出文件中包含一组航路非劣解集。该文件作为下一代Map的输入会被云平台分割成许多数据段,设计每个数据段包含一个航路非劣解,传给一个Map,并放入该Map的非劣解集,引导蚂蚁求解。优良解保持策略加快问题的求解速度,使算法具有较好的收敛性。

(3)解多样性保持策略:采用文献［12］基于Shannon的信息熵理论来保持解的多样性。对航路非劣解集中的多个航路计算其想相似度和解密度。解密度计算如函数4所示,h为信息熵,表示解的混乱程度。Reduce函数中第8步根据解密度进行信息素更新,式(6)中ΔτLij=1/((1+di)×Q),或ΔτDij= 1/((1+di)×Q),Q为参数。样解密度di小的航路信息素增加较大,其上导航点被选中的概率增大,增大解的覆盖范围,保持了求解的多样性。

函数4 解密度计算函数

4 仿真实验及分析

4.1 实验环境、参数及数据

硬件环境为:Intel Core i5 CPU,2.80 GHz;4 GB内存;100 MB带宽;10台微机。软件包括VMware Workstation,Ubuntu,hadoop,jdk,eclipse等。实验运行在hadoop云平台中,实验参数选定为:α=β=1,ρ=0.05,Q=100,Nant=10×网格行数,威胁区内网格的初始信息素为0,其余网格的初始信息素为1,这样使无人机不能进入威胁区。

实验数据分2组:第1组为小规模数据,第2组为较大规模数据。小规模数据用来展示求解结果和收敛性;较大规模数据用来考查算法的求解效率和扩展性。

第1组小规模数据:无人机搜索空间为(0,0)至(100,100)km。起始点S、终点G坐标为(0,50), (100,50)。各种威胁及影响飞行的因素归于搜索空间内的5个威胁区中,各威胁区中心坐标为(15,65), (30,45),(60,50),(80,20),(85,70),半径为:10 km, 10 km,15 km,15 km,10 km;搜索空间划分为50×50网格(记为Grid50×50),网格间距为2。设最大转向角为60°;最大飞行距离为120(可以根据需要设定。若较大,则会得到很多非劣解。本文设置较小,这样得到的非劣解较少,方便结果展示)。

第2组较大规模数据:将上述航路规划问题的搜索空间扩大4倍,即为(0,0)至(200,200);随机生成威胁区个数、位置及半径;行、列网格数从50扩大到100, 200,400,500,即网格从Grid50×50扩大到Grid100×100,Grid200×200,Grid400×400,Grid500×500。其他条件不变。

4.2 RPMA性能分析

设计实验1来考查和展示RPMA求解结果。为了方便结果展示,选用第1组小规模数据,RPMA求解结果如图3所示。

RPMA得到15个非劣航路,其目标函数值见表1,目标函数值的分布情况如图4所示,其中,L为航路长度;D为航路到威胁区距离。取图4中最下点(目标函数值L,D分别为(113.254 85,303.039 15)、中间一点(117.383 85,376.222 84)和最上点(119.855 99, 450.178 77)所对应非劣解来展示航路情况,即分别对应图3中航路R1,R2,R3。

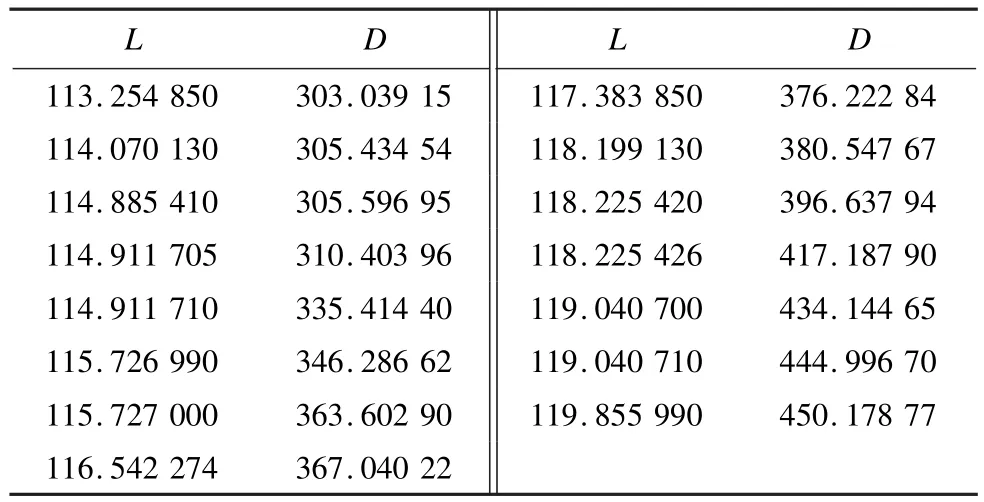
表1 RPMA得到的15个非劣航路的目标函数值

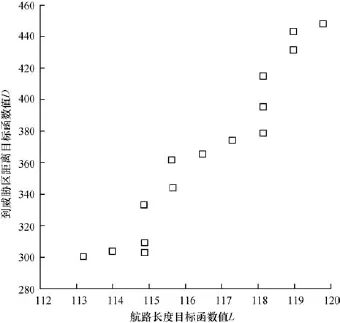
图4 RPMA得到的非劣航路目标函数值分布

航路选择:RPMA可以预先规划出多条航路,可根据飞行任务的不同选择不同的航路,或在飞行过程中根据不同需要临时决定选择合适的飞行航路。例如,若要求飞行的航路最短(或飞行时间最短、油耗最小),可以选择表1第1列(图4最下点)目标函数值对应的航路(图3中的R1),这时虽然航路最短,但到威胁区距离也最小,危险性最大;若要求无人机飞行时危险性最小,可以选择表1最后一列(图4最上点)目标函数值对应的航路(图3中的R3),这时到威胁区距离最大,危险性最小,但航路最长,飞行时间最长;若兼顾航路长度和飞行危险,可选择图4中间点对应的航路。

RPMA的收敛性:算法RPMA连续运行10次得到表1中全部非劣航路时迭代次数(代数)分别为41,35,38,50,49,32,30,46,28,37,即平均38.6代算法得到全部非劣,算法收敛。图5为RPMA在最大第50代得到全部非劣的实验中,非劣解集的进化情况。其中,G1,G2,G3分别为在第5代、第15代和第50代时RPMA得到的当前非劣解集,第50代时RPMA求得全部非劣解集,由于RPMA中应用了最优解保持策略,这时算法收敛,可以看出算法收敛速度较快。

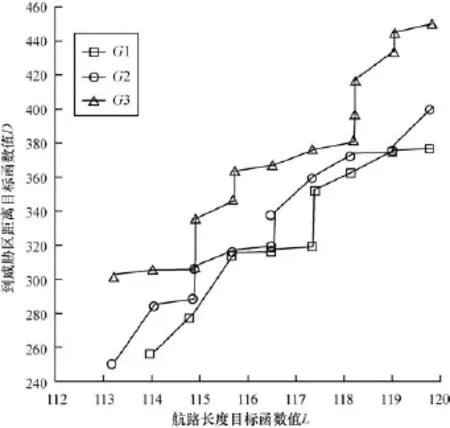
图5 RPMA收敛过程

优化策略比较:设计实验2来比较采用和不采用优良解保持和解多样性保持策略的求解结果。设优良解保持和解多样性保持2种策略都采用的算法为A1,即本文的RPMA算法;仅采用优良解保持策略的算法为A2;仅采用解多样性保持策略的算法为A3;2种策略都不采用的算法为A4;蚂蚁选点方式优化策略为基本优化策划在A1～A4中都采用。A2～A4的求解结果如表2所示,A1结果见表1。

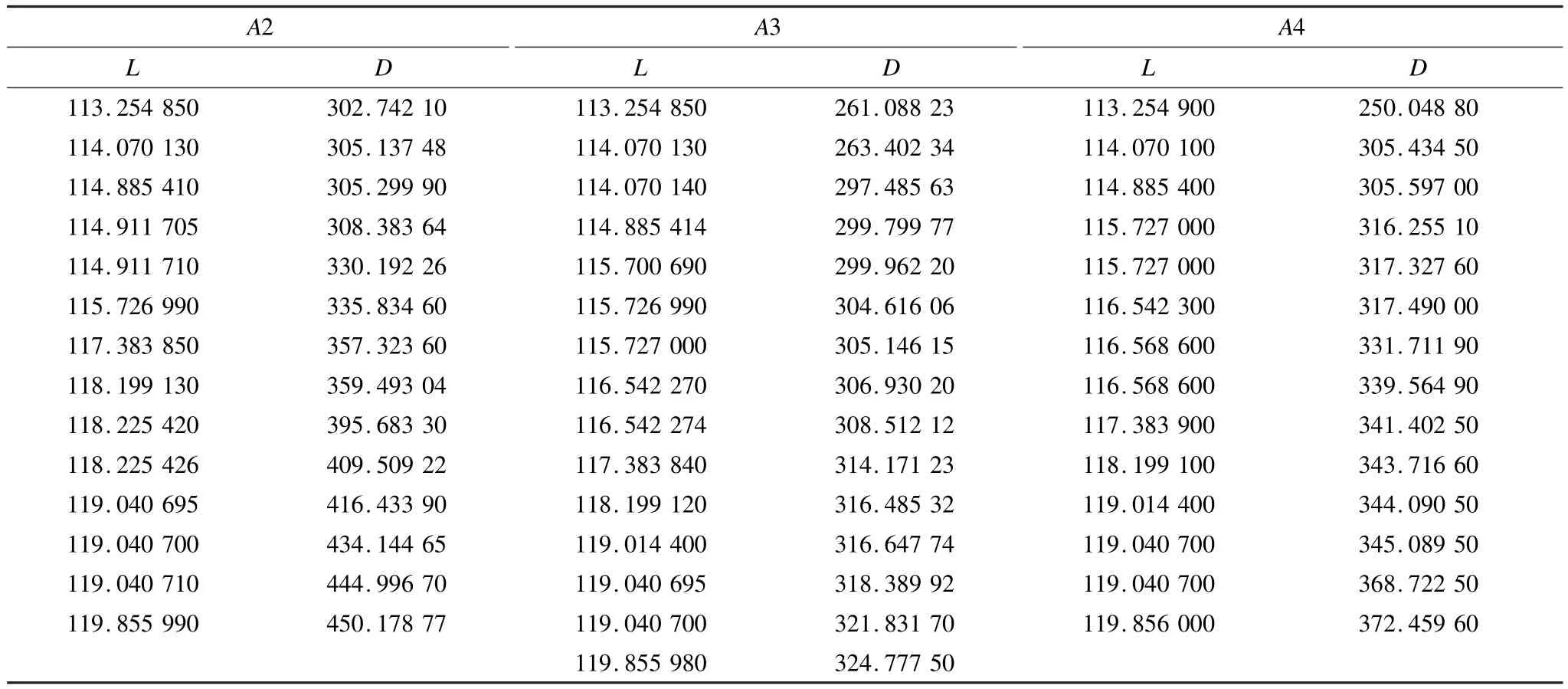
表2 算法A2～A4得到非劣航路的目标函数值比较

图6展示了A1～A4求解结果比较,其中,各算法得到相应结果时运行的代数分别为:A1为70,A2为189,A3为600,A4为1 000。可以看出A1的求解结果优于其他算法,说明优化后的RPMA求解性能有较大的提高。这是因为优良解保持策略使优解得以保留,对蚂蚁求解起到引导作用,加速问题的求解和收敛过程;解多样性保持策略使相似度小的解,信息素增加较大,使蚂蚁能冲出局部最优解,有效地改善了常规蚁群算法易于收敛于局部优解的缺陷。

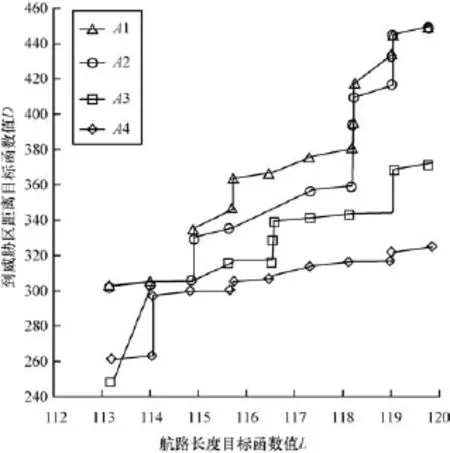
图6 优化策略求解结果比较

综合上述可以看出,RPMA能容易得到问题的非劣解集,RPMA求解航路问题是可行、有效的,且收敛速度快,收敛稳定。

RPMA扩展性:采用第2组较大规模数据,设计实验3来考查RPMA的扩展性。RPMA在云平台中运行的时间分为两大类:平台消耗的时间和问题求解的时间。由图2-RPMA的执行流程可以看出, RPMA的每一代求解为一个任务job,可分为5个阶段:job开始到Map开始的文件分割、任务部署阶段(所需时间记为t1),Map函数执行阶段(时间为t2),Map结束到Reduce开始的对Map的结果进行排序、归并、传输阶段(时间为t3),Reduce函数执行阶段(时间为t4),Reduce结果的输出阶段(时间为t5)。从粗粒度到细粒度的网格划分,RPMA连续运行10次,每代的平均运行时间如表3所示。可以看出,云平台消耗的时间t1,t3,t5基本稳定,为运行任务所必需的额外开销,问题求解时间包括Map时间t2、Reduce时间t4,t2随着计算量的迅速增大才显著变化。当网格数增大16倍时(从100×100到400× 400),RPMA运行总时间才增加50 s,说明算法RPMA具有较好的扩展性。

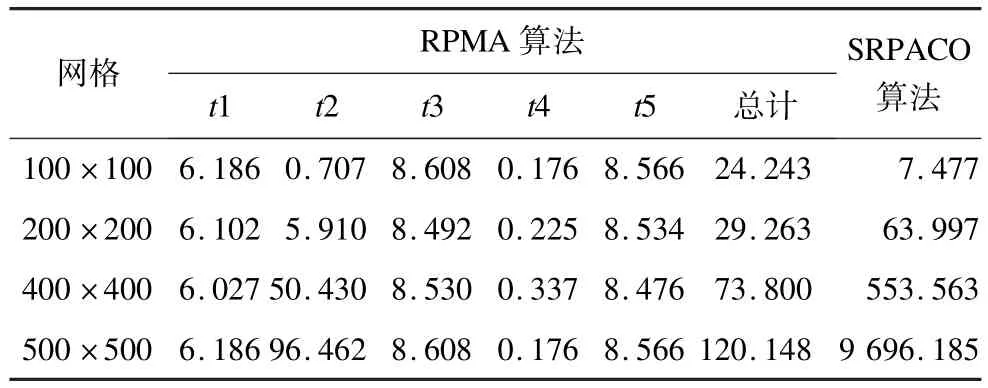
表3 运行时间比较 s

串并行算法比较:利用实验3来比较串并行算法运行效率。设RPMA的Map数量为10,在单机串行环境下运行,并采用上述策略优化后的常规蚁群算法为SRPACO,SRPACO的参数同RPMA,SRPACO在不同网格划分下的运行时间如表3所示。从表3可以看出,当网格划分粒度较粗100×100(计算量较小)时SRPACO求解速度优于RPMA,这是因为RPMA的平台消耗时间比例大,对小规模问题求解意义不大;但当网格划分粒度较细时,SRPACO运行时间迅速增加,而RPMA总时间最大仅增加1分多钟,说明RPMA对大规模问题求解效率高,体现云计算分布式并行计算的优势,适合求解大规模问题。

5 结束语

本文提出了基于MapReduce和多目标蚁群算法的航路规划算法(RPMA),应用 MapReduce和HDFS等云计算技术在hadoop云计算平台中分布式并行地求解航路规划问题,增强了对大规模、细粒度的航路规划问题的处理能力;设计了求解航路规划问题的多目标蚁群算法,应用多目标优化的方法,同时优化航路长度和威胁目标函数,得到多条非劣航路;无人机可在飞行前或飞行过程中根据实际飞行需求从多条非劣航路中选择最合适的飞行航路,一定程度满足了无人机飞行的实时性和灵活性;采用蚂蚁选点方式优化策略、优良解保持策略和解多样性保持策略对蚁群算法进行优化,有效改进了蚁群算法的求解时间长和易于收敛到非最优解的缺陷。实验结果表明,RPMA求解航路规划问题性能良好,适合在分布式并行的云计算平台中运行,具有对大规模数据的处理能力。蚁群算法参数的进一步优化选择及在大规模的机群中验证和改进算法的性能是下一步的研究方向。

［1］郑昌文,严 平,丁明跃,等.飞行器航迹规划研究现状与趋势［J］.宇航学报,2007,28(6):1441-1446.

［2］郑昌文,李 磊,徐帆江,等.基于进化计算的无人飞行器多航迹规划［J］.宇航学报,2005,26(2):223-227.

［3］梁 宵,王宏伦,曹梦磊,等.无人机复杂环境中跟踪运动目标的实时航路规划［J］.北京航空航天大学学报,2012,38(9):1129-1133.

［4］胡中华,赵 敏,刘世豪,等.基于自适应蚁群算法的无人飞行器航迹规划［J］.计算机集成制造系统,2012,18(3): 560-564.

［5］梁 宵,王宏伦,李大伟,等.基于流水避石原理的无人机三维航路规划方法［J］.航空学报,2013,34(7):1670-1681.

［6］严江江,丁明跃,周成平.基于进化算法的多飞行器四维航迹规划方法［J］.系统仿真学报,2009,21(4):1125-1129.

［7］Dean J,Ghemawat S.MapReduce:Simplified Data Processing on Large Clusters［C］//Proceedings of the 6th Symposium on Operating System Design and Implementation.Berkeley,Germany:USENIX Association,2004: 137-150.

［8］Dean J,Ghemawat S.Distributed Programming with Mapreduce［M］//Oram A,Wilson G.Beautiful Code. Sebastopol,USA:O’Reilly Media,Inc.,2007:371-384.

［9］Dean J,GhemawatS.MapReduce:Simplified Data Processing on Large Clusters［J］.Communications of the ACM,2008,51(1):107-113.

［10］Dorigo M.Optimization Learning and Nature Algorithms［D］.Milan,Italy:Department of Electronics, Politecnico di Milano,1992.

［11］王会颖,倪志伟,吴 昊.求解多维背包问题的 Map Reduce蚁群算法［J］.计算机工程,2013,39(4):248-253.

［12］Kapur J,Kesavan H.Entropy Optimization Principles with Applications［M］.San Diego,USA:Academic Press,1992.

编辑 金胡考

Route Planning Algorithm Based on MapReduce and Ant Colony Optimization

BO Luo,ZHAO Gangyao
(School of Aeronautical Manufacturing Engineering,Nanchang Hangkong University,Nanchang 330063,China)

Route planning is an effective way to improve the ability to survive of Unmanned Aerial Vehicle(UAV),for which can make the UAV reach the destination safely and fast.In this paper,the route planning algorithm based on MapReduce and multi-objective Ant Colony Optimization(ACO)is put forward,which named RPMA.The multiobjective ACO algorithm is designed in the RPMA and different varieties of optimization strategies are used to improve the RPMA.The RPMA uses cloud computing technology and makes it solve the route planning problems in distributed cloud computing environment and parallel technology.A number of paths are planned in advance.The RPMA is able to make the UAV choose different routes according to different missions or choose the appropriate route according to different temporary needs.The preferable result is got in the simulation experiment,which indicates that the RPMA is an efficient way to solve the route planning problems and has the qualities of convergence and scalability.In addition,the RPMA has the handling abilities of large-scale data.

cloud computing;MapReduce distributed programming;Ant Colony Optimization(ACO);route planning;Unmanned Aerial Vehicle(UAV);Hadoop Distributed File System(HDFS)

1000-3428(2015)05-0038-07

A

TP301

10.3969/j.issn.1000-3428.2015.05.007

国家自然科学基金资助项目(51165037);江西省自然科学基金资助项目(20114BAB216005);江西省教育厅青年科学基金资助项目(GJJ12452)。

柏 硌(1994-),男,本科生,主研方向:智能算法,云计算;赵刚要,副教授、博士。

2014-06-03

2014-07-30E-mail:boluo_69@163.com

中文引用格式:柏 硌,赵刚要.基于MapReduce与蚁群优化的航路规划算法［J］.计算机工程,2015,41(5):38-44,55.

英文引用格式:Bo Luo,Zhao Gangyao.Route Planning Algorithm Based on MapReduce and Ant Colony Optimization［J］. Computer Engineering,2015,41(5):38-44,55.