不完整大数据的分布式聚类填充算法

冷泳林,陈志奎,张清辰,鲁富宇

(1.渤海大学信息科学与技术学院,辽宁锦州121000;2.大连理工大学软件学院,辽宁大连116620)

不完整大数据的分布式聚类填充算法

冷泳林1,2,陈志奎2,张清辰2,鲁富宇1

(1.渤海大学信息科学与技术学院,辽宁锦州121000;2.大连理工大学软件学院,辽宁大连116620)

传统大数据填充算法是根据整个数据集对缺失数据进行填充,使得填充值容易受到不同类别数据的干扰,导致填充结果不精确。针对该问题,给出不完整数据的相似度度量方法,使用近邻传播(AP)算法对不完整数据进行聚类。采用云计算技术优化AP聚类算法,实现一种基于MapReduce的分布式聚类算法,根据算法聚类结果将同一类数据对象划分到相同簇中,并利用同一类对象的属性值对缺失值进行填充。实验结果表明,该算法能实现不完整大数据的聚类,同时加快聚类速度,提高缺失数据的填充精度。

不完整大数据;近邻传播聚类;云计算;数据填充;不完整信息系统

1 概述

近年来,复杂网络发展迅速,尤其是物联网应用,已经深入到生活各领域。在物联网中,大量传感终端在非人工监控状态下工作,这些传感终端很容易出现各种故障,从而造成采集数据含有缺失值,即不完整数据［1-2］。数据不完整性严重影响物联网应用,因此,对不完整数据进行分析和填充对物联网与复杂网络的发展具有重要意义。

传统缺失数据填充算法如基于决策树的填充方法、基于马氏距离的填充方法及基于最大期望(Expectation-Maximization,EM)和贝叶斯网络的数据填充方法［3-4］等,大部分是基于概率分布等假设,利用整个数据集对缺失数据进行填充,未充分考虑数据对象的类别特征,使得填充值容易受到不同类别对象的干扰,严重降低填充结果的准确性。近邻传播(Affinity Propagation,AP)聚类算法由Frey在2007年提出［5-6］,AP聚类算法中数据间的距离可采用任意度量方法,无需满足三角不等式或距离对称等约束条件,也无需事先指定聚类中心和聚类个数,同时算法聚类结果稳定。采用AP算法对不完整数据进行聚类时,由于AP聚类算法在带有缺失数据的不完整数据集中,无法直接度量数据对象之间的相似度,因此不能直接应用AP聚类算法对不完整数据集进行聚类。针对上述问题,本文提出一种基于聚类分析的不完整数据填充算法,首先对不完整数据进行聚类,将同一类对象划分到相同簇中,通过同一类对象对缺失数据进行填充,避免其他对象对填充值的干扰,提高填充结果的精确性。给出一种新的不完整信息系统的相似度度量方式,度量不完整数据对象间的相似度,进而利用AP聚类算法对不完整数据集进行聚类。另外,传统聚类算法难以满足大数据聚类的实时性要求,因此,本文利用云计算技术对AP聚类算法进行优化,实现基于MapReduce的分布式AP聚类算法,加速聚类算法的执行速度。

2 相关知识

2.1 不完整信息系统

定义1(不完整信息系统) IS=(U,A,V,f)是一个信息系统,其中,U是论域,即研究对象的集合; A是属性集合,同时A=φ,属性A包含2种属性,分别是条件属性和决策属性,条件属性用C表示,决策属性用D表示,集合A,C,D之间满足如下关系: A=C∪D且C∩D=φ;V是U中的对象在属性A下的取值集合,f是信息函数,用来把论域中的对象和属性与取值做映射,即。当x∈U,a∈C时,有f(x,a)=∗,表示f(x,a)的函数值未知。这种带有未知函数值的信息系统叫做不完整信息系统,用IIS表示。

定义2(不完整信息系统中对象取值相同的概率) 给定IIS=(U,A,V,f),x∈U且y∈U,A=C∪D,a∈C,C是条件属性,D是决策属性。如果Va是属性a的值域,那么实体x,y在属性a下取值相同的概率Pa(x,y)定义如下:

(3)当f(x,a)=f(y,a)时,Pa(x,y)=1;

(4)当f(x,a)和f(y,a)都不为∗,且不相等时, Pa(x,y)=0。

由上面定义可得,对象相似度计算如下:

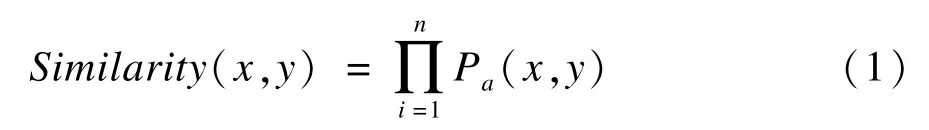
其中,n代表对象属性个数,即对象相似度等于每个属性相同的概率之和。

2.2 MapReduce计算模型

MapReduce是一种简化的分布式编程模型和高效的任务调度模型,用于大规模数据集的并行运算。利用该模型,用户可以自定义Map和Reduce函数来实现分布式算法。数据文件首先被划分成小块,以(key,value)的数据形式输入到函数Map中,输出一系列新的(key′,value′),如式(2)所示。MapReduce框架收集所有Map的输出,并按照key′值分组汇聚。最后每个 key′对应的组(key′,list(value′))按照式(3)输入到同一个Reduce函数中,用于生成新的value′′值。

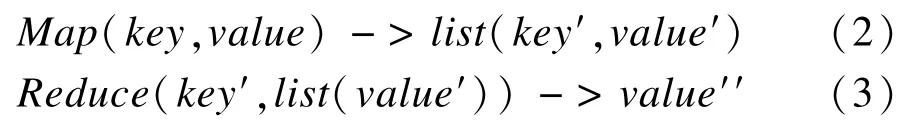
2.3 AP聚类算法

AP聚类算法定义数据点之间传递2类消息,即吸引度(responsibility)和归属度(availability)。吸引度用来描述节点适合作为其他点的聚类中心的代表程度,r(i,k)表示节点k对节点i的吸引度,从节点i指向节点k,是节点k成为节点i的聚类中心的累积证据。归属度用于描述节点选择另一个节点作为聚类中心的适合程度。a(i,k)表示节点i对节点k的归属度,从节点k指向节点i,是节点i归属于节点k的累积证据。

AP聚类算法通过迭代更新吸引度矩阵R=［r(i,k)］与归属度矩阵A=［a(i,k)］,逐步确定高质量聚类中心,用归属度矩阵与相似度矩阵S=［s(i,k)］更新吸引度矩阵R:

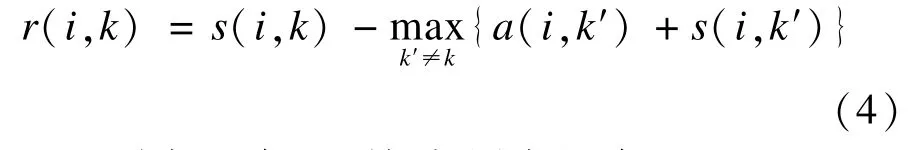
用吸引度矩阵R更新归属度矩阵A:

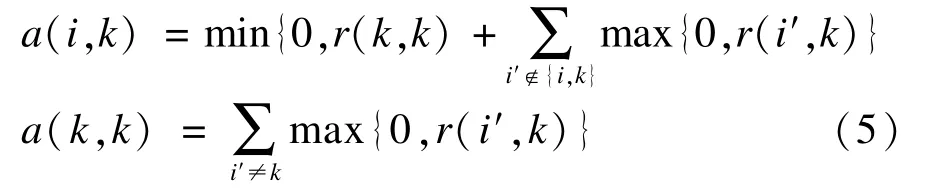
其中,s(i,k)为点i到点k的相似度,表明点k作为点i的聚类中心的合适程度;r(i,k)表示点k对点i的吸引度,反映点k通过与其他数据点k′竞争,作为适合数据点i的聚类中心的程度;a(i,k)表示点i对点k的归属度,反映数据点i选择数据点k作为其聚类中心的适合程度。当i=k时,s(k,k)由输入的偏向参数p(k)设置,p(k)越大,数据点k越有可能被选为聚类中心,聚类个数越多;反之,p(k)越小,聚类个数越少。

3 基于近邻传播的不完整数据聚类算法

本文提出一种基于近邻传播的不完整数据聚类算法,直接对不完整数据集进行聚类。设整个数据对象集合为O,且O={o1,o2,…,on},集合O中每个对象由 m个属性{a1,a2,…,am},即 A={a1, a2,…,am}为属性集合。算法首先将整个数据集划分为C和I 2个集合,即O=C∪I,其中,C={c1, c2,…,ct};I={i1,i2,…,ip};C∩I=φ且t+p=n;C为完整数据集,即C中所有数据对象的属性值都是完整的;I为非完整数据集,即I中所有数据对象都存在缺失属性值。在划分完成后,利用近邻传播算法对完整数据集C进行聚类,这样可以避免带有缺失属性的数据对象对聚类结果造成干扰。最后利用本文提出相似度度量方式将非完整数据集I中的数据对象划分到完整数据集中的相应簇中。

3.1 数据预处理

在数据对象的属性集合中存在一部分离散属性,为了能够使离散型属性直接参与计算,本文采用相似度距离将离散属性转化为数值属性,即n维数据来表示一个具有n个不同取值的离散属性,通过这种转换规则,可以保证聚类过程中不会因为转换而损失信息,即不同属性之间的相互距离为1,相同属性之间的距离为0。

为消除因为属性取值范围不同所产生的不平衡性,需要将所有的属性值归一化到一个确定的数值范围内,使不同的属性拥有相同的权重值,本文采用标准偏差来归一化属性集中的连续特征值。

3.2 基于区间划分的不完整信息系统相似度度量

传统的不完整信息系统的相似度度量方式存在以下不足:一方面无法度量连续数值属性的相似度,另一方面对离散属性的相似度进行度量时会产生大量0值,即一旦2个数据对象的某个属性的属性值不相等时,2个数据对象的相似度为0,不符合数据对象的相似度规律。为此,本文重新定义了不完整信息系统的相似度度量。

对于连续数值属性,本文提出一种基于区间划分的相似度度量方式。设完整数据集C聚类后得到k个簇,C={C1,C2,…,Ck},这些簇满足以下条件: Ci≠φ,i=1,2,…,k;Ci∩Cj=φ,i,j=1,2,…,k;。

设第i个簇Ci中数据对象的第j个属性aj为连续型数值属性,且其在该簇中的取值范围为[x,y]。用表示第i个簇的数据中心ci在第j个属性上的取值,显然,∈［x,y］。定义2个相似度度量系数α和 β,其中,。

对于非完整数据集I中的任一数据对象b,设其在第j个属性aj上的取值为abj。数据对象b与ci在属性aj下取值相同的概率Paj(b,ci)定义如下:

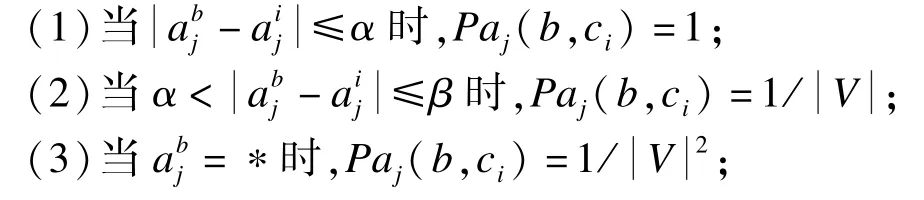
对于离散属性而言,设第i个簇Ci中数据对象的第k个属性ak为离散型属性。用表示第i个簇的数据中心ci在第k个属性上的取值。对于非完整数据集I中的任一数据对象b,设其在第k个属性ak上的取值为。数据对象b与ci在属性aj下取值相同的概率Pak(b,ci)定义如下:

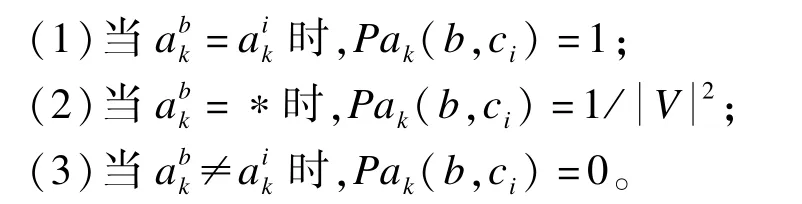
为避免传统相似度度量产生大量0值的不足,本文根据上面定义给出非完整数据集I的数据对象b与完整数据集任意簇中心ci的相似度计算:

其中,q代表连续型数值属性的个数;k代表离散型属性个数。

3.3 不完整数据聚类算法

本文提出的基于AP算法的不完整数据聚类算法主要步骤如下:

(1)将数据集O划分为完整数据集C与非完整数据集I,即O=C∪I。

(2)将完整数据集C中数据对象离散属性值转换为数值,将C中所有数据对象的属性值进行归一化处理。

(3)计算数据集C中数据对象的相似度矩阵S。

(4)初始化吸引度矩阵R和归属度矩阵A,根据式(4)、式(5)更新吸引度矩阵R和归属度矩阵A。

(5)直到聚类中心不再发生变化,或者已经完成指定的迭代次数后,停止计算,否则重复步骤(4)。

(6)对角线值a(k,k)+r(k,k)＞0的数据点k为自动发现的聚类中心,而对于数据点i,使其a(i, k)+r(i,k)最大的候选类中心为其真正归属的聚类中心。

(7)针对数据集C中的连续型数值属性,计算其在每个簇中的相似度度量系数α和β。

(8)将非完整数据集I中所有数据对象划分到相应簇中,即根据式(6)计算I中数据对象到每个簇中心的相似度,选择与其相似度最大的簇中心作为其聚类中心。

3.4 算法复杂度分析

本文提出的基于AP的不完整数据聚类算法的时间复杂度分析具体如下:

(1)数据集O划分,遍历数据集的每个对象确定其是否含有缺失属性,时间复杂度为O(n),n为数据集中数据对象的数目。

(2)计算数据集C中的数据对象间的相似度矩阵,时间复杂度为O(t2),t为数据集C中数据对象的数目。

(3)更新吸引度矩阵和归属度矩阵,时间复杂度均为O(kt2),k是迭代次数。

(4)划分数据集I中数据对象到相应的簇中,时间复杂度为O(sp),s是簇的数目,p是I中数据对象的数目。

因此,总体时间复杂度为T=O(n)+O(t2)+ O(kt2)+O(sp),当n＞＞t时,算法时间复杂度近似为O(n)+O(t2),否则算法时间复杂度近似为O(t2),即算法的时间花费主要在于计算数据集C中对象间的相似度、更新吸引度矩阵与归属度矩阵。

4 不完整数据聚类算法的并行化设计

当n＞＞t时,执行算法的主要时间花费在划分数据集O和利用AP算法对数据集C进行聚类,在利用AP算法对数据集C进行聚类的过程中,主要是更新吸引度矩阵与归属度矩阵。本文利用MapReduce对以上步骤进行分布式并行计算,降低算法的时间代价,提高算法运行效率。

4.1 数据集划分的MapReduce并行化设计

为使得数据集O的划分能够适合MapReduce计算模型处理,首先将待处理的数据记录以行形式存储,使待处理数据能够按行分片,且片间数据无相关性,分片过程由MapReduce运行环境完成。

Map函数设计:Map函数的任务是确定数据对象所属的集合。输入数据记录＜key,value＞对的形式为＜行号,记录行＞,其中,行号是指数据对象所处的行;记录行由数据对象的属性构成。Map函数扫描输入的每个记录的所有属性,根据每个记录是否含有属性值为空的属性,为记录做集合标记,即如果记录oi含有属性值为空的属性,则将oi的集合标记为I,表示该记录被划分到非完整数据集I;否则,将记录oi的集合标记为C,表示该记录被划分到完整数据集 C,输出结果 ＜key,value＞对的形式为＜集合标号,行号＞。

Reduce函数设计:Reduce函数的任务是根据Map函数得到的中间结果,将同一集合的数据记录合并。输入数据记录＜key,value＞对的形式为＜集合标号,行号＞,集合标号对应每条记录的集合标记,具有相同集合标记的记录送往一个 Reduce, Reduce负责将同一个集合内的记录写入一个数据表文件。

在串行条件下,将数据集O划分为数据集C和数据集I的时间复杂度为O(n),n是数据集O中数据对象的数目。为衡量基于MapReduce的并行数据集划分方法,定义符号C用于衡量在分布式平台中,计算过程产生的通信代价。对于分布式计算而言,数据划分的总体时间复杂度为O(n/p)+C(n/d),其中,p代表参与计算的节点数目;d代表数据传输带宽。

4.2 更新吸引度矩阵的MapReduce并行化设计

利用AP算法对完整数据集C进行聚类的过程中,需要不断迭代更新吸引度矩阵r(i,k)。

通过吸引度计算式(4)可知,计算吸引度矩阵的第ith行的吸引度r(i,k)时,需要使用的数值是完全相同的,分别是相似度矩阵中的第ith行的值,即s(i, k′),k′={1,2,…,n}和归属度矩阵的第ith的值,即a(i,k′),k′={1,2,…,n}。除此之外,吸引度矩阵中每个元素的计算之间具有独立性。这2个特性保证吸引度矩阵的更新计算适合MapReduce并行化设计。为减少MapReduce并行化实现过程中的通信代价,本文将相似度矩阵、吸引度矩阵和归属度矩阵按行划分为p块,每块具有t/p行,其中,t是数据集C中数据对象的数据;p是参与运算的云节点数目。划分完成后,本文将每一块的吸引度计算放到一个Map任务中执行,从而实现不同行的吸引度可以分布在不同机器上并行执行。

在串行环境下,每更新一次吸引度矩阵的时间复杂度为O(t2),对于分布式计算而言,每更新一次吸引度矩阵的时间复杂度为O(t2/p)+C(t/d),由于MapReduce并行化计算过程中,采用中间结果本地化存储,因此在迭代过程中,采用本文并行设计方法不会增加通信代价［7］。

对于更新归属度矩阵的MapReduce并行化设计,其思路和方法同更新吸引度矩阵的MapReduce并行化设计类似,只需对吸引度矩阵和归属度矩阵进行按列分块,本文不再赘述。

5 基于聚类与信息熵的数据填充算法

在对数据进行聚类后,本文利用与缺失属性的对象在同一个簇中的数据对象的相应属性的加权值作为该属性的预测值。这种方法的关键在于确定各数据对象的加权系数,为能够客观准确地确定加权系数,本文采用信息论中熵值的概念［8］,通过数据对象间的相似度提供的信息来确定加权系数。

对于任意缺失属性的对象o,设与其处在同一簇中的完整数据对象分别为o1,o2,…,om,基于聚类与信息熵的不完整数据填充算法主要步骤如下:

(1)根据3.2节计算o与o1,o2,…,om的相似度,记为s1,s2,…,sm。

(2)将s1,s2,…,sm按照式(7)进行单位化:

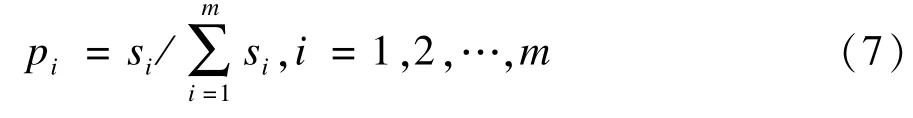
(3)按照式(8)计算每个完整数据对象的熵值:

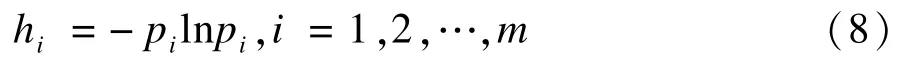
(4)按照式(9)计算每个对象的权重:

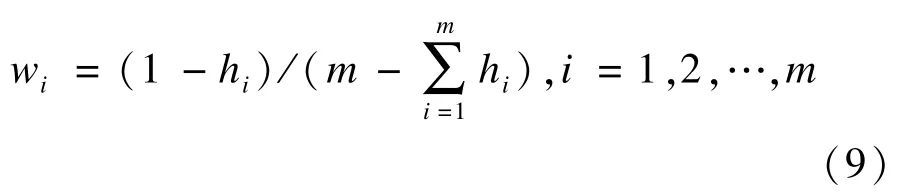
(5)按照式(10)计算对象o缺失属性值f:

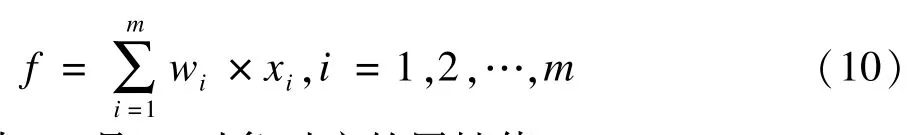
其中,xi是oi对象对应的属性值。

6 实验结果与分析

实验数据集使用从数字家庭实验室采集的真实数据。数字家庭是以计算机技术和物联网技术为基础,各种家电通过不同的互连方式进行通信及数据交换,实现家用电器之间的“互联互通”,使人们足不出户就可以更加方便快捷地获取信息,从而极大提高人类居住的舒适性和娱乐性。数字家庭数据包括安防系统数据、室内温湿度数据、家电设备使用状态等数据。本数据集包含108个数据对象,每个数据对象包含40个属性,数据集大小是80 GB。

6.1 基于AP的不完整数据聚类性能分析

为测试本文算法性能,评价聚类效果,进行2组实验,实验中使用聚类精度［9］对聚类结果进行评价,聚类精度具体描述如下:

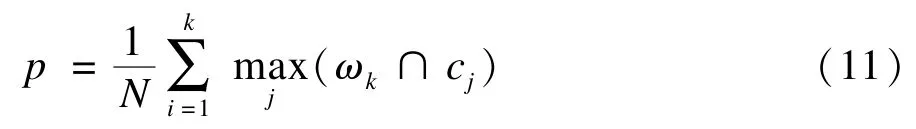
其中,ωk表示聚类后的第k个集合;cj表示数据真实分类后的第j个集合。

(1)随机地从原始数据集P中选出4%,8%, 12%,16%,20%,24%的数据对象,删除这些数据对象中的部分属性值,模拟不完整数据集O。利用AP算法分别对原始数据集P、不完整数据集O和完整数据子集C进行聚类,实验结果如图1所示。

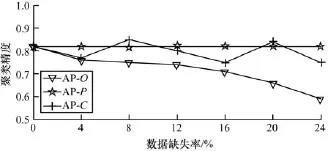
图1 不同数据缺失率下的数据聚类精度比较

在图1中,由于AP聚类算法具有稳定性,即对同一批原始数据集P进行多次聚类,结果相同,其精度保持在82%左右。在对完整数据子集C进行聚类时,由于C中没有缺失属性,其聚类精度近似于AP对原始数据集P的聚类精度。当非完整数据集I中含有对聚类结果造成负面影响的离群点时,AP对数据集C聚类时,将不会受到这些离群点的影响。因此,此时AP对数据集C的聚类精度高于AP对原始数据集P的聚类精度。反之,AP对数据集C的聚类精度低于AP对原始数据集P的聚类精度。在对不完整数据集O进行聚类时,由于受到非完整数据集I的影响,因此从整体上看,AP对不完整数据集O的聚类精度低于AP对原始数据集P和完整数据子集C的聚类精度。非完整数据集I所占的比重越多,对聚类准确度的影响越大,所以,聚类精度越低。当非完整数据集I所占比重在20%以内时,聚类精度能够保持在70%以上,能够满足大数据聚类的误差范围。当非完整数据集I所占比重超过20%以上,聚类精度急剧降低。

(2)从原始数据集中分别选取不同数目的数据对象构成8个数据集,每个数据集的数据对象数目分别为 10 000,20 000,30 000,40 000,50 000, 60 000,70 000和80 000。随机地从这8个数据集中选择10%的数据对象,删除这些数据对象中的部分属性,模拟8个不完整数据集O。每批数据集均可划分为完整数据集C和非完整数据集I2个子集。利用本文提出的不完整数据聚类算法分别对这8个数据集的O和C进行聚类,聚类结果如图2所示。

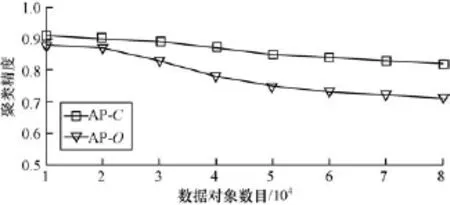
图2 不同数据对象数目下的聚类精度比较

在图2中,AP算法对完整数据集C进行聚类精度曲线表明,随着数据量的增大,噪音数据越来越多,聚类精度有所下降,但是总体聚类精度保持在80%以上,充分验证了AP算法的有效性。但由于受到非完整数据集I的影响,算法对数据集O的聚类精度低于AP算法对数据集C的聚类精度。随着数据量的增加,本文算法的聚类精度逐渐降低,当数据量超过30 GB时,聚类精度趋于稳定,验证了本文算法对大规模不完整数据聚类的有效性。

6.2 基于MapReduce的不完整数据聚类性能分析

为测试基于MapReduce的不完整数据聚类算法的性能,本文进行如下2组实验:

(1)分别利用一台机器和具有10个节点的云计算平台执行本文算法,执行结果如图3所示。

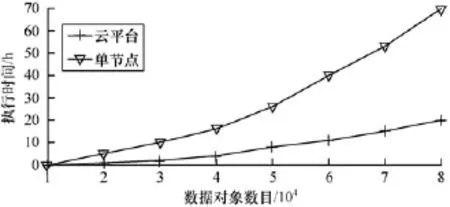
图3 算法并行执行时间

从图3可以看出,随着数据量的增长,算法在单节点和云平台上的执行时间都在增加。在单节点上串行执行的时间随着数据的增长,呈现指数级增长,这是由于单节点算法的时间复杂度近似为O(n2)。而在云平台上算法的执行时间低于单节点执行时间。尤其在数据对象数目超过50 000条后,算法的分布式运行时间远低于单节点执行时间,表明基于MapReduce的不完整数据聚类算法在处理大数据方面的高效性。

(2)加速比是衡量一个系统在扩展性优劣的主要指标,其主要测试当计算硬件资源增加时,对于相同规模作业的系统处理能力。为测试本文提出的并行算法的加速比,分别选择5个、10个、15个、20个、25个节点执行本文算法,考察在逐渐增加节点的情况下,系统完成任务的时间,实验结果如图4所示。

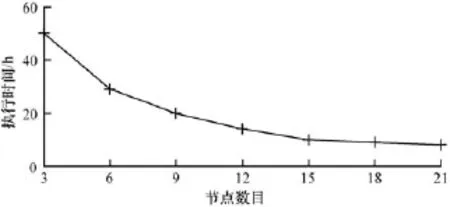
图4 算法加速比实验结果

从图4可以看出,每个作业运行时间都随着节点的增加而降低,增加的节点可以显著提高系统对同规模数据的处理能力,说明云计算在本文聚类算法上具有较好的加速比。然而,当节点数目超过12个后,增加节点之后算法的运行时间降低的不明显,原因在于随着节点增加,算法通信量和通信时间急剧增加。

6.3 基于信息熵的不完整数据填充性能分析

为测试本文提出的不完整数据填充算法的性能,实验中使用符合指数［10］(d2)作为填充精度的评估条件,符合指数d2用于评估真实值和估算值之间的相似度。

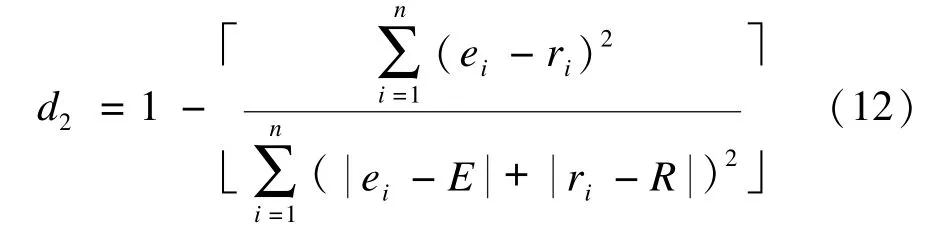
其中,n表示缺失值总数;ri表示第i行缺失的真实值;ei表示第i行缺失值的估算值;R表示真实值ri的平均值;E表示估算值ei(i=1,2,…,N)的平均值。当d2值越高,表示估算值与真实值越匹配。

(1)随机地从原始数据集P中选出4%,8%, 12%,16%,20%,24%的数据对象,删除这些数据对象中的部分属性值,模拟不完整数据集O。为测试本文算法性能,将本文基于聚类和信息熵的不完整数据填充算法CAIE(Incompleted Data Filling Based on Clustering and Information Entropy)与基于朴素贝叶斯的EM缺失数据填充算法(EMBNB)［11］、基于不完备数据聚类的缺失数据填充算法(MIBOI)［12］进行比较,实验结果如图5所示。

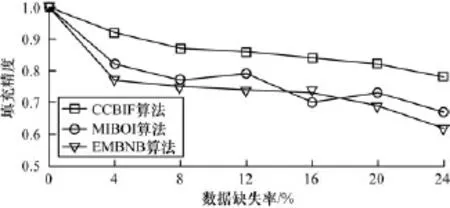
图5 算法在不同缺失率下的填充精度比较

从图5可以看出,随着数据缺失率的增长,3种算法的填充精度均有所降低。在3种算法中,CAIF算法填充精度最高,原因是CAIF算法有效避免了不同类对象对数据填充的影响。除此之外,当数据缺失率超过15%时,随着缺失数据的增加,基于朴素贝叶斯的EM缺失数据填充算法与基于不完备数据聚类的缺失数据填充算法的填充精度［12］急剧降低,而CAIF算法则比较稳定,说明CAIE算法对缺失率较高的数据集依然能保持良好的效果。

(2)从原始数据集中分别选取不同数目的数据对象构成8个数据集,每个数据集的数据对象数目分别为10 000个、20 000个、30 000个、40 000个、50 000个、60 000个、70 000个和80 000个。随机地从这8个数据集中选择10%的数据对象,删除这些数据对象中的部分属性,模拟8个不完整数据集O。分别利用3种算法对这8个数据集进行填充,填充结果如图6所示。从图6可以看出,随着数据对象的增加,数据中的噪声数据和错误数据越来越多,因此,3种算法的填充精度都有所降低。当数据对象个数超过60 000时,随着数据量的增加, EMBNB和MIBOI 2种算法的数据填充精度急剧降低,而CAIF算法的填充精度一直能够稳定在80%以上,表明CAIF算法在填充大数据方面的优越性。

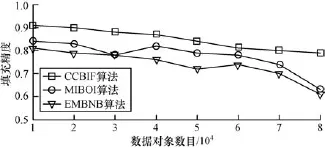
图6 算法在不同数据对象数目下的填充精度比较

7 结束语

随着物联网、电子商务、社交网络应用的广泛深入,复杂网络得到迅速发展。复杂网络产生的数据量越来越大,数据的不完整性问题日益突出。本文针对不完整大数据填充问题,利用不完全信息系统理论度量不完整数据对象间的相似度,在此基础上利用AP算法对不完整数据进行聚类。为加快大数据的聚类速度,利用云计算思想实现基于MapReduce的分布式AP不完整数据聚类算法,根据数据聚类结果对不完整数据进行填充。实验结果表明,本文算法能够有效地对不完整数据进行聚类及填充。下一步将从数据对象的属性出发,进一步提高不完整数据的填充质量。

［1］Cui Liying,Soundar K,Reka A.Complex Networks:An Engineering View［J］.IEEE Circuits and Systems Magazine,2010,10(3):10-25.

［2］孟晓峰,慈 祥.大数据管理:概念、技术与挑战［J］.计算机研究与发展,2013,50(1):146-169.

［3］刘星毅,檀大耀.基于马氏距离的缺失数据填充算法［J］.微计算机信息,2010,26(3):225-227.

［4］Jerez J M,Molina I,García-Laencina P J,et al.Missing Data Imputation Using Statistical and Machine Learning Methods in a Real Breast Cancer Problem［J］.Artificial Intelligence in Medicine,2010,50(2):105-115.

［5］Twala B,Jones M C,Hand D J.Good Methods for Coping with Missing Data in Decision Trees［J］.Pattern Recognition Letters,2008,29(7):950-956.

［6］Frey B J,Dueck D.Clustering by Passing Messages Between Data Points［J］.Science,2007,315(5814): 972-976.

［7］温 程.并行聚类算法在MapReduce上的实现［D］.杭州:浙江大学,2011.

［8］Schroeder M J.An Alternative to Entropy in the Measurement of Information［J］.Entropy,2004,6(5): 388-412.

［9］林秀丹,毛国君.基于密度网格的分布式数据流聚类算法［J］.计算机工程,2012,38(16):70-73.

［10］Rahman G,Islam Z.A Decision Tree-based Missing Value Imputation Technique for Data Pre-processing［C］// Proceedingsofthe 9th Australasian Data Mining Conference.Darlinghurst,Australia:Australian Computer Society,Inc.,2011:41-51.

［11］李 宏,阿玛尼.基于EM和贝叶斯网络的丢失数据填充算法［J］.计算机工程与应用,2010,46(5): 123-125.

［12］武 森,冯晓东.基于不完备数据聚类的缺失数据填补方法［J］.计算机学报,2012,35(8):1726-1738.

编辑 陆燕菲

Distributed Clustering and Filling Algorithm of Incomplete Big Data

LENG Yonglin1,2,CHEN Zhikui2,ZHANG Qingchen2,LU Fuyu1
(1.College of Information Science and Technology,Bohai University,Jinzhou 121000,China;
2.School of Software Technology,Dalian University of Technology,Dalian 116620,China)

Traditional big data filling algorithms fill missing values depending on the statistical theory of the data set, and they are corrupted by noise data which decrease the imputation accuracy.This paper proposes an algorithm to fill missing values based on distributed incomplete big data clustering.It clusters incomplete big data directly by proposing a new similarity metrics,and uses cloud computing technology to improve clustering efficiency by designing MapReducebased distributed Affinity Propagation(AP)clustering algorithm.The data in the same cluster is utilized to fill missing values.Experimental result demonstrates the proposed algorithm can cluster the incomplete big data directly and improve the filling accuracy of missing data effectively.

incomplete big data;Affinity Propagation(AP)clustering;cloud computing;data filling;incomplete information system

1000-3428(2015)05-0019-07

A

TP311

10.3969/j.issn.1000-3428.2015.05.004

国家自然科学基金资助项目(U1301253);中国高等职业技术教育研究会规划课题基金资助项目(GZYGH1213036,GZYGH 1213035);辽宁省自然科学基金资助项目(2013020014);辽宁省社会科学基金资助项目(L14AGL002)。

冷泳林(1978-),女,讲师、博士研究生,主研方向:大数据处理,数据库技术;陈志奎,教授、博士;张清辰,博士研究生;鲁富宇,助教、硕士。

2014-06-09

2014-08-05E-mail:lengyonglin@qq.com

中文引用格式:冷泳林,陈志奎,张清辰,等.不完整大数据的分布式聚类填充算法［J］.计算机工程,2015,41(5):19-25.

英文引用格式:Leng Yonglin,Chen Zhikui,Zhang Qingchen,et al.Distributed Clustering and Filling Algorithm of Incomplete Big Data［J］.Computer Engineering,2015,41(5):19-25.