基于绑定图的Web服务可靠性预测模型

谢春丽,王书芹

(江苏师范大学计算机科学与技术学院,江苏徐州221116)

基于绑定图的Web服务可靠性预测模型

谢春丽,王书芹

(江苏师范大学计算机科学与技术学院,江苏徐州221116)

为提高动态组合服务的可靠性预测精度,提出一种适用于Web动态服务的可靠性预测模型。将Web服务分解为执行路径、服务组合模块、原子服务等不同粒度的组合单位,构建各组合单位的绑定图,在绑定图的基础上按照粒度大小逐层进行可靠度预测,并将组合单位的可靠度集成为组合服务的可靠度。实例分析结果表明,与现有可靠性预测模型相比,当组合服务中服务组件的可靠度发生变化时,该模型只需计算受该服务影响的执行路径上的可靠度增量,降低了计算复杂度,并且能更高效地进行灵敏度分析以识别组合服务中的关键服务。

组合服务;动态预测模型;可靠性;绑定图;组合模块

1 概述

随着Web服务的快速发展,越来越多的业务借助Web组合服务来实现,因此如何确保组合服务的可靠性成为人们最关注的问题。服务的动态组合允许在服务运行期间动态选择服务组件,并且当服务组件的服务质量(Quality of Service,QoS)不满足用户要求或者绑定的服务组件已不可用时,允许在运行期间重新绑定到新的服务组件,这使得组合服务的运行服务是动态改变的。

Web服务复杂的运行环境使得Web服务更容易发生失效［1-3］,因此传统的可靠性模型已经不能适用新的面向服务的软件开发模式。文献［4-5］扩展了传统的可靠性模型,用Markov链描述服务之间的结构关系。文献［6］提出一个分层可靠性模型,将Web服务分为数据层、服务层、服务池层以及组合服务逻辑层,分别讨论每层的失效过程。文献［7］从服务请求过程可能出现的失效进行可靠性建模,把服务请求分为3个层次,分别是服务请求层、管理层以及网络层。服务请求层主要考虑请求超时失效,管理层讨论服务请求的资源匹配失效,网络层探讨服务请求执行过程中的网络连接失效。文献［8］提出基于Petri的可靠性预测方法。文献［9］提出用户协同的可靠性模型,通过研究相似用户的历史失效数据来预测Web服务对当前用户的可靠度。Web服务的组合过程其实是一个业务流过程,因此,根据工作流结构预测组合服务的可靠性也是一种常用方法［10-11］。但是,Web服务不同于传统软件,具有动态性,而目前组合服务的可靠性模型大多以设计阶段为基础,未考虑运行时的动态调整。因此,本文提出一个适用于动态组合服务的可靠性预测模型,当组合服务中某些服务的可靠性发生变化时,该模型无需重新计算整个组合服务的可靠度,具有较高的计算效率。

2 相关术语定义

任何一个组合服务都是一个组合流程,在动态组合过程中,组合流程中的服务一般都是抽象服务(Abstract Service,AS),没有绑定到具体服务,当服务在执行时,绑定到的服务称为具体服务［3］。

定义1 服务绑定图(Service Binding Graph, SBG):控制流图(Control Flow Graph,CFG)常用来表示组合服务之间的结构关系,但是用CFG表示组合服务时,未能表示服务的动态绑定过程,因此,对CFG进行扩展,在CFG中明确标出该抽象服务绑定到具体服务的情况,如图1所示,抽象服务AS1可由{W1,W2,W3}中的任何一个服务实现,绑定概率分别为{1/3,1/3,1/3}。

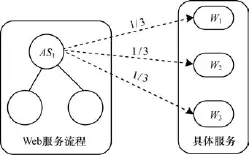
图1 服务绑定图

定义2 服务组合模块(Service Composition Module,SCM):由原子服务根据一定的结构关系组合而成的服务模块集。SCM={Ass,OP},其中,Ass是组合模块中的原子服务集;OP是定义原子服务之间操作关系的操作符,OP∈{Sequence,Choice,Loop,Concurrence}。根据服务之间的操作关系,将服务组合模块分为顺序模块SM、选择模块CM、循环模块LM和并行模块CoM。

定义3 组合服务的执行路径Path:组合服务的执行一般由多条路径按照一定的概率执行,记Path={＜Path1,P1＞,＜Path2,P2＞,…,＜Pathm,Pm＞},其中,Pathi表示第i条执行路径,Pathi= {S1,S2,…,Sn}。

3 Web服务可靠性的动态预测模型

本文将Web组合服务逐层分解为执行路径、组合模块、原子服务等不同粒度的基本组合单位。Web组合服务的可靠度通过这些基本组合单位的可靠度来度量。

3.1 原子服务可靠度

在给定一个抽象原子服务后,与其相匹配的具体原子服务可以有多个,Web服务根据不同用户要求在不同时刻可以绑定到不同的具体服务。例如抽象原子服务AS与其匹配的具体服务有3个,分别为{W1,W2,W3},3个原子服务的可靠度分别记为R1,R2,R3,则原子服务AS的可靠度Ra可以通过下式进行计算:

随着服务绑定的改变,原子服务AS的可靠度Ra需要重新计算:

3.2 组合模块可靠度

Web服务组合模块根据组合方式可以分为顺序模块SM、选择模块CM、循环模块LM和并行模块CoM,其服务绑定图如图2所示。

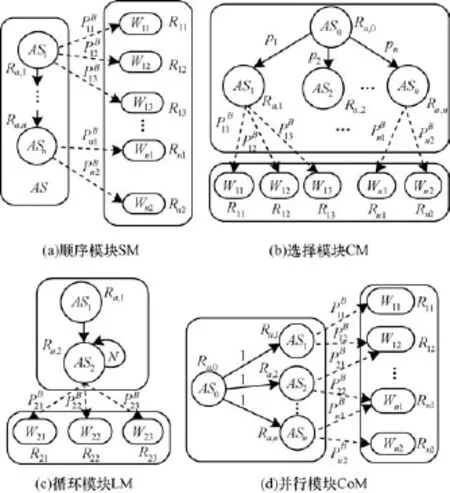
图2 组合模块的服务绑定图

组合模块可靠度具体如下:

(1)顺序模块SM

顺序模块由抽象服务AS1,AS2,…,ASn顺序组成,具体原子服务Wij的可靠度分别为Rij(1≤i≤n),则顺序模块SM的可靠度计算如下:

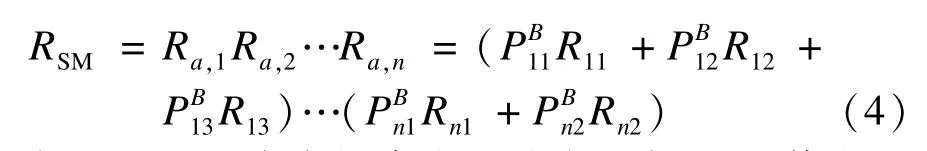
如果AS1的绑定概率发生改变,则Ra,1的值发生改变,进而影响顺序模块的可靠度RSM。顺序模块SM的新可靠度RSM′计算如下:

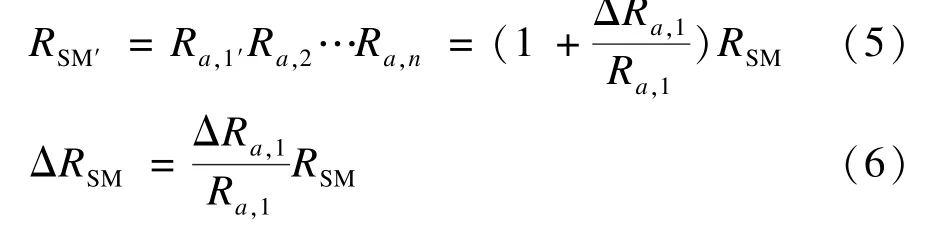
(2)选择模块CM

选择模块中AS0执行后,按照概率p1,p2,…,pn分别选择执行抽象服务AS1,AS2,…,ASn,其中,AS1的可靠度为Ra,1。AS1可以绑定到{W11,W12,W13}中的任何一个服务,绑定概率分别为{PB11,PB12,PB13},类似地,ASn可以绑定到{Wn1,Wn2}中的任何一个服务,则选择模块CM的可靠度计算如下:

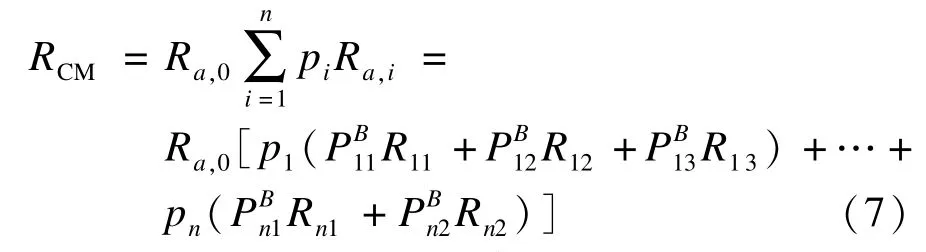
如果抽象服务AS1的可靠度发生改变,新的可靠度Ra,1′=Ra,1+ΔRa,1,则有:

其中,ΔRCM=p1Ra,0ΔRa,1。

(3)循环模块LM

AS2模块被反复执行N次,AS2可以绑定到{W21,W22,W23}中的任何一个服务,循环模块LM的可靠度计算如下:

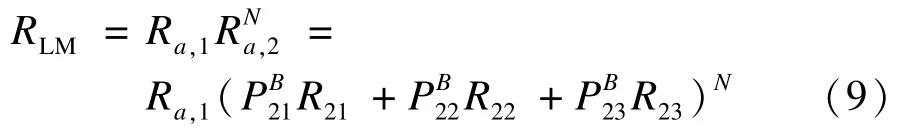
如果抽象服务AS2的绑定发生变化,则循环模块LM的可靠度可以根据以下公式重新计算:

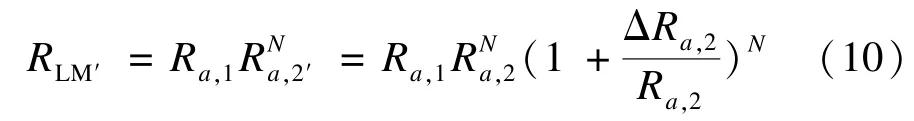
(4)并行模块CoM

并行模块CoM由抽象服务AS0,AS1,…,ASn组成,并行模块的可靠度计算如下:

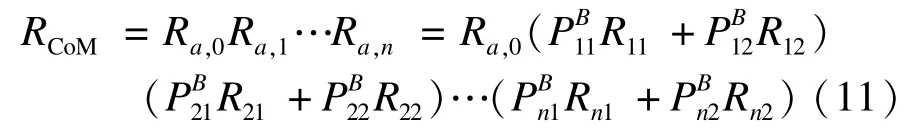
如果抽象服务AS1的绑定被改变,则并行模块的可靠度可由以下公式重新计算:

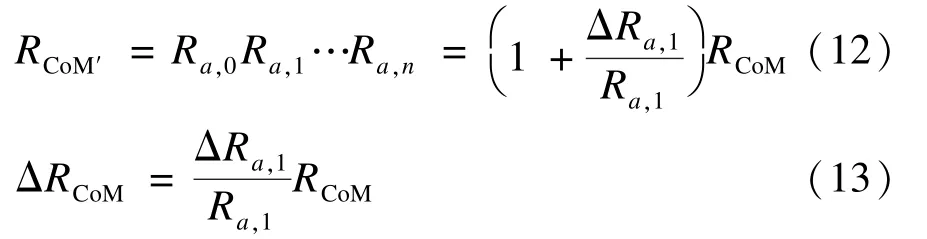
从上述公式可以看出,当组合模块中的某一个抽象服务的可靠度发生改变时,只需通过简单的计算就可得出组合模块的可靠度。

3.3 路径可靠度

Web服务的一条执行路径表现为该条路径上所有服务(原子服务、服务模块)的顺序结构关系,如图3所示。路径1由{AS0,CoM,AS5}以顺序结构组成,首先根据3.2节的公式分别计算出AS0,CoM,AS5的可靠度,则路径1的可靠度计算如下:

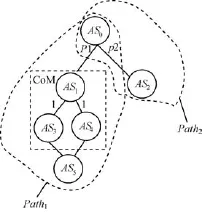
图3 路径的服务绑定图

如果路径上某一个服务的绑定被改变,例如W5,其可靠度被重新计算后,可用以下公式重新计算路径的可靠度:

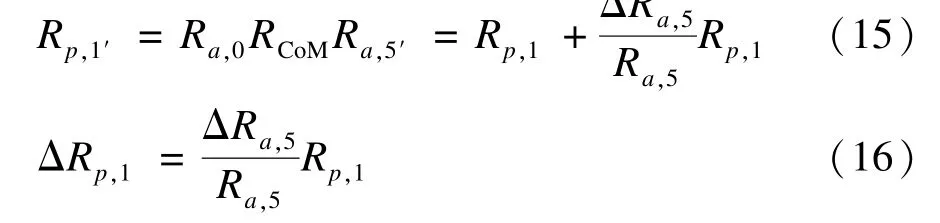
3.4 组合服务可靠度

由于任何一个组合服务的执行都是由几条路径按照一定的概率组合而成的,因此组合服务的可靠性是多条执行路径上的可靠性的概率组合。如图3所示,该组合服务CoS有2条执行路径Path1和Path2。路径的执行概率分别为P1,P2,因此组合服务CoS的可靠度计算如下:

如果执行路径Path1的可靠度发生变化,则新的组合服务可靠度可以表示为:

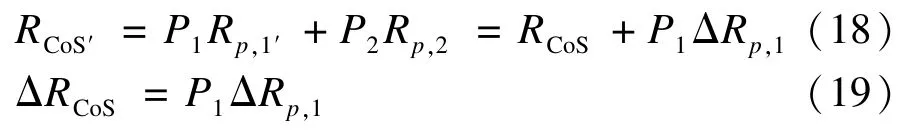
如果n条执行路径的可靠度发生改变,则组合服务可靠度的增量为:

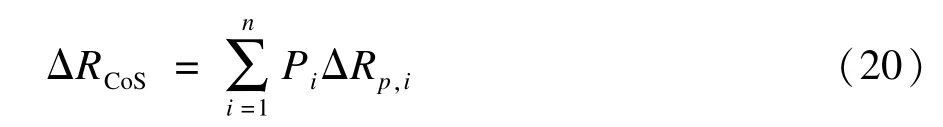
可以看出,对于组合服务来说,当某一个服务发生改变时,只要重新计算该服务所在的执行路径上的可靠性,无需重新计算整个组合服务的可靠度,大大减少了计算的复杂性。

4 组合服务的可靠性增量模型

组合服务可以逐层分解为粒度较小的路径、组合模块和原子服务等组合单位,因此组合服务的可靠度也可以分解为路径、组合模块和原子服务的可靠度。

下文将研究当执行路径、组合模块、原子服务中任意一组合单位的可靠度发生改变时,如何计算组合服务的可靠度。

4.1 组合单位间的关系

本文用一个实例详细说明当组合服务中的某一个原子服务的绑定发生改变时,如何调整组合服务的可靠度。如图4所示的组合服务CoS,其中各模块的关系如下:

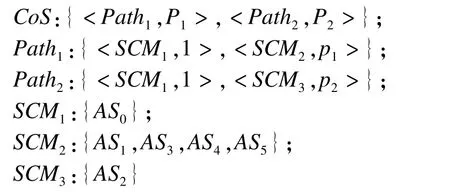
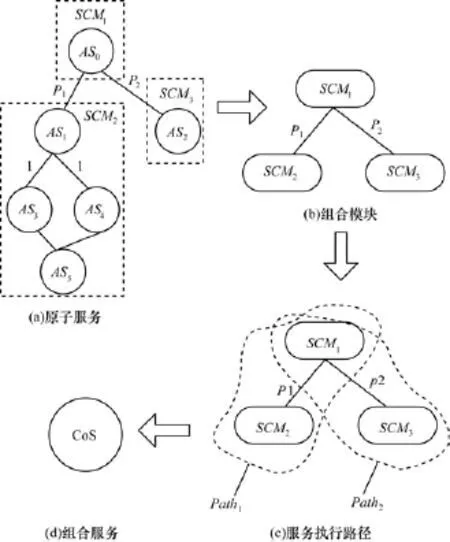
图4 组合服务CoS

利用各组合单位之间的关系可以方便地计算组合单位的可靠度增量。

4.2 组合服务可靠度计算过程

在进行组合服务的可靠度计算过程中,首先将组合服务中的原子服务根据结构关系(图4(a))划分为组合模块(图4(b)),然后划出各执行路径(图4(c)),其可靠度计算步骤如下:

(1)根据式(1)计算原子服务的可靠度Ra。

(2)在原子服务的可靠度基础上,识别各组合模块的类型,该实例中,SCM1,SCM3属于顺序模块,SCM2属于并行模块,根据式(4)和式(11),计算组合模块的可靠度RSCM1,RSCM2,RSCM3。

(3)在服务组合模块的可靠度基础上,根据式(14),计算执行路径的可靠度RP,1,RP,2。

(4)在执行路径的可靠度基础上,根据式(17),计算组合服务的可靠度RCoS。

当某个原子服务的绑定(例如AS1)发生改变时,根据以下步骤,计算组合服务可靠度的增量ΔRCoS:

(1)找到AS1所从属的所有组合模块SCM2,根据式(12)计算SCM2的可靠度增量ΔRSCM2。

(2)找到SCM2从属的所有执行路径Path1,根据式(16)计算Path1的可靠度增量ΔRp,1。

(3)根据式(19)计算组合服务CoS的可靠度增量ΔRCoS,如果有多个原子服务的可靠度发生改变,则重复步骤(1)～步骤(3)。

从上述步骤可以推出组合服务可靠度的增量可以按照如下递推公式进行计算:

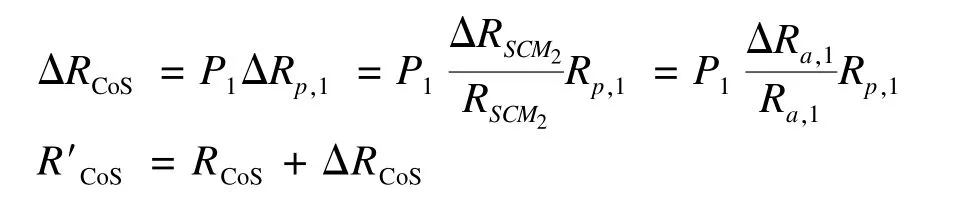
5 实验结果与分析

5.1 实例

以一个旅游服务系统(图5)作为实例,介绍组合服务可靠度动态增量模型。

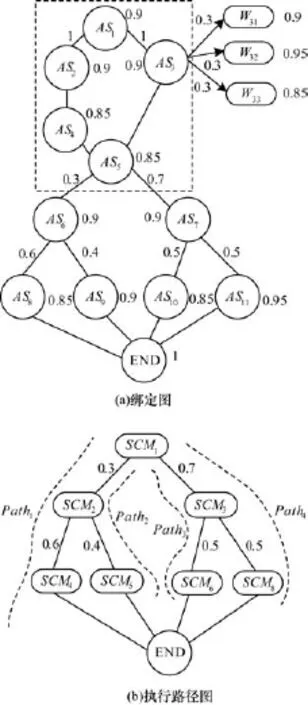
图5 旅游服务系统实例

在图5(a)中,仅给出了AS3的服务绑定图,其他抽象原子服务的服务绑定图不再列出,而是直接标示每个抽象原子服务的可靠度Ra。图5(b)是将实例进行路径划分后的执行路径图,从中可以看出该旅游服务由4条执行路径{Path1,Path2,Path3,Path4}组成,原子服务{AS1,AS2,AS3,AS4,AS5}构成并行组合模块SCM1。

5.2 计算精度比较

根据5.1节的分析结果以及图5中标出的原子服务可靠度,计算各组合单位的可靠度,计算结果如表 1所示。为比较动态可靠性模型(Dynamic Reliability Model,DRM)的计算精度,以面向用户的可靠性模型(CUORM)作为比较对象［4］。根据文献［4］的计算过程可知RCUORM=0.422,与本文计算结果相比(表1中RCoS)发现这2种方法计算出的结果是一样的。

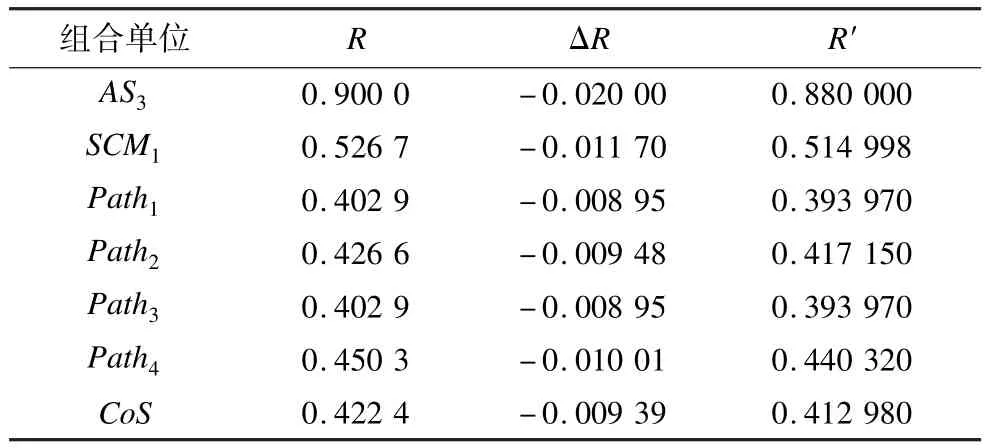
表1 组合单位的可靠度

5.3 可靠度增量模型的计算结果比较

假如AS3的绑定发生改变,则AS3的可靠度也会发生改变,从而影响SCM1,Path1,Path2,Path3,Path4。此处用ΔRa,3表示AS3的可靠度增量,SCM1,Path1,Path2,Path3,Path4,CoS的增量可靠度可以根据下列公式进行计算:

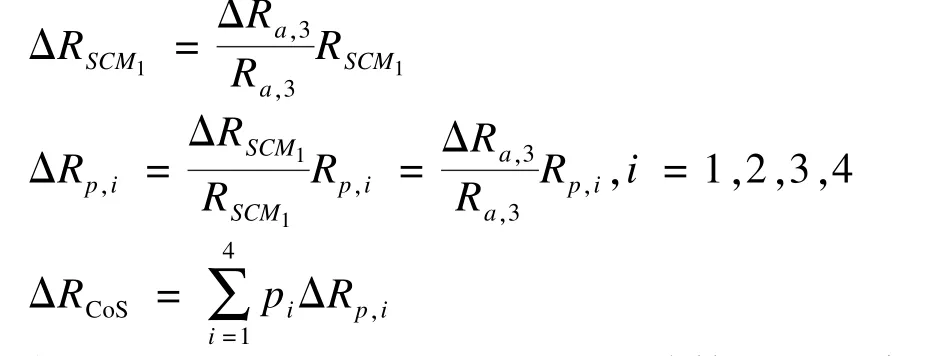
假设ΔRa,3=0.02,利用上述公式计算出的组合单位的新的可靠度如表1中R’列所示。组合服务CoS的新的可靠度Rcs′按照以下公式进行计算:

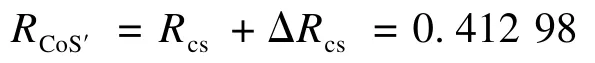
采用CUORM方法重新计算组合服务的可靠度。

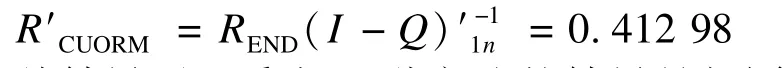
从结果可以看出,2种方法的结果是相同的,但是从计算过程可以看出本文DRM方法比CUORM方法更加简单,计算量大大减少。

5.4 灵敏度分析

组合服务的灵敏度体现出当其中某一个原子服务或者服务组件发生改变时对组合服务的影响大小,此处定义组合服务对原子服务ASi的灵敏度为:

其中,Ci值越大说明该原子服务的可靠度对组合服务的可靠度有较大影响。在本文实验中,采用单因素分析法,首先设置某一原子服务的可靠度从0.95变化到1,而其他所有的原子服务或者服务组件的可靠度都设为0.95。

以AS3为例,推出组合服务对原子服务的灵敏度,当AS3的可靠度发生改变时,可靠度受到影响的执行路径有{Path1,Path2,Path3,Path4}。

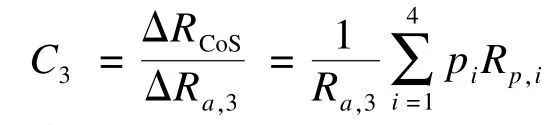
本文方法利用式(21)可以更灵活地计算每个原子服务的灵敏度。表2中给出组合服务对原子服务ASi(i=1,2,…,11)的灵敏度。

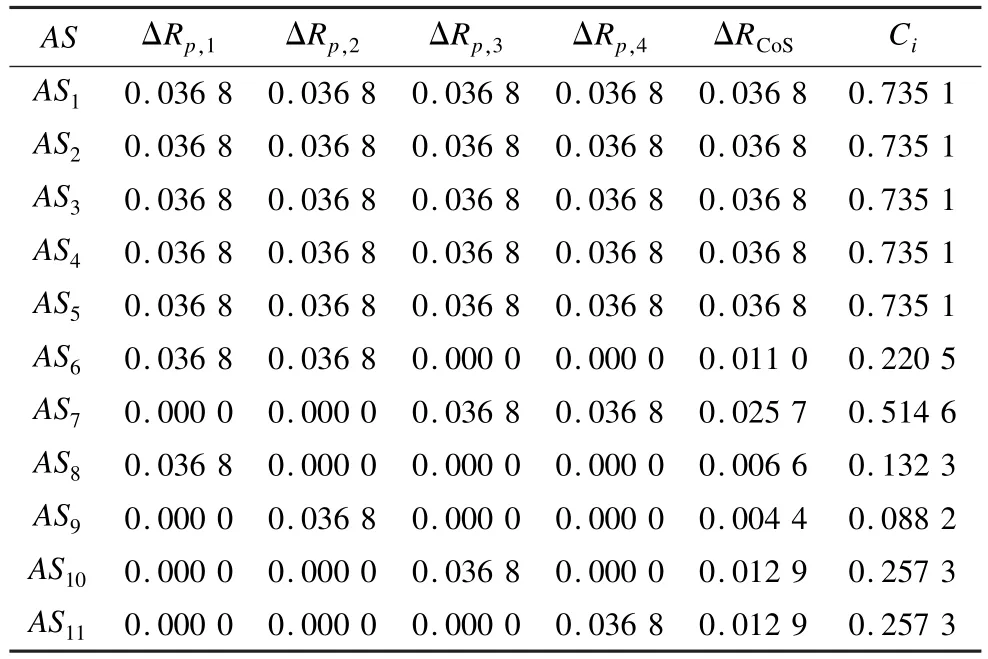
表2 组合服务对原子服务ASi的灵敏度

从灵敏度分析可以看出,AS1,AS2,AS3,AS4,AS5的灵敏度是相同的,并且是最大的,而{AS1,AS2,AS3,AS4,AS5}∈SCM1,这说明SCM1的可靠度对整个组合服务的可靠度影响是最大的。而AS9的灵敏度是最小的,这是因为AS9∈Path2,而Path2的执行概率是最小的,所以AS9的可靠度对整个组合服务的可靠度影响最小。

6 结束语

本文提出一个适用于Web动态服务的可靠性预测模型。该模型首先将Web服务分解为执行路径、组合模块、原子服务等不同组合粒度的组合单位,然后分层计算各组合单位的可靠度,最后组合服务的可靠度可以通过组合单位可靠度进行计算。当某一个服务的可靠度发生变化时,该模型只需计算受该服务影响的执行路径上的可靠度增量即可,而无需重新计算所有可靠度,因此该方法更简单有效,尤其适合Web服务的动态环境。

通过实验结果比较验证了本文方法的有效性和正确性,该方法在计算各原子服务对组合服务的影响时更简单灵活。在按照组合粒度对组合服务进行分解时,发现每个组合服务都有多个不同的分解方案,对于结构复杂的组合服务如何选择一种合适的分解方案,使得分解后的组合单位在计算可靠度时更简便是下一步需要重点研究的内容。

［1］Yu Qi,Liu Xumin,Bouguettaya A,et al.Deploying and Managing Web Services:Issues,Solutions and Directions［J］. Very Large Data Bases Journal,2008,17(3):537-572.

［2］岳 昆,王晓玲,周傲英.Web服务核心支撑技术:研究综述［J］.软件学报,2004,15(3):428-442.

［3］白成刚,苏 亮,赵迎春,等.网络服务可靠性与运行剖面变化率有关吗［J］.计算机研究与发展,2008, 45(12):2044-2051.

［4］Cheung R C.A User-oriented Software Reliability Model［J］. IEEE Transactions on Software Engineering,1980,6(2): 118-125.

［5］Grassi V.Architecture-based Reliability Prediction for Service-oriented Computing［M］//de Lemos R.Architecting Dependable Systems III.Berlin,Germany:Springer-Verlag, 2004:279-299.

［6］Wang Lijun,BaiXiaoying,Zhou Lizhu,etal.A Hierarchical Reliability Model of Service-based Software System［C］//Proceedings of the 33rd Annual International Computer Software and Applications Conference. Washington D.C.,USA:IEEE Press,2009:199-208.

［7］Dai Yuanshun,Pan Yi.A Hierarchical Modeling and Analysis for Grid Service Reliability［J］.IEEE Transactions on Computers,2007,56(5):681-691.

［8］Albu R D,Florin P V A Prototype for Web Services Reliability Prediction［J］.InternationalJournalof Information and Communication Technology,2013, 5(1):64-74.

［9］Zheng Zibin,Lyu M R.Collaborative Reliability Prediction for Service-oriented Systems ［C］// Proceedingsofthe32nd ACM/IEEE International Conference on Software Engineering.Washington D.C., USA:IEEE Press,2010:35-44.

［10］Zo Hang-Jung,NazarethD L,JainH K.Measuring Reliability of Applications Composed of Web Services［C］// Proceedings of the 40th Hawaii International Conference on System Sciences.Washington D.C.,USA:IEEE Press, 2007:278-280.

［11］童安玲,黄玉划,曹玲玲.能量受限无线传输的可靠性分析［J］.计算机工程,2013,39(5):106-109.

编辑 陆燕菲

Reliability Prediction Model for Web Service Based on Binding Graph

XIE Chunli,WANG Shuqin
(School of Computer Science and Technology,Jiangsu Normal University,Xuzhou 221116,China)

In order to improve the prediction accuracy of reliability for composite services,this paper proposes a new dynamic prediction model for Web service reliability.A composite service is divided into executing path,service composite module and atomic service according to composite grain.Binding graphs for composite unites are built,and the reliability models for the composition unites are presented based on these binding graphs.The reliability models are integrated for composite services.Example analysis result show that,compared with the traditional reliability prediction model,the proposed model only computes the updated reliability,reduces the computation complexity,and a more flexible sensitivity analysis is performed to determine which service component has the most significant impact on the improvement of composite service reliability.

composite service;dynamic prediction model;reliability;binding graph;composite module

1000-3428(2015)05-0014-05

A

TP311

10.3969/j.issn.1000-3428.2015.05.003

国家自然科学基金资助项目(61304174,61304117);江苏师范大学博士学位教师科研支持基金资助项目(9213614101)。

谢春丽(1979-),女,讲师、博士,主研方向:软件可靠性建模与分析;王书芹,博士研究生。

2014-05-08

2014-07-10E-mail:xcl_bhb@163.com

中文引用格式:谢春丽,王书芹.基于绑定图的Web服务可靠性预测模型［J］.计算机工程,2015,41(5):14-18,25.

英文引用格式:Xie Chunli,Wang Shuqin.Reliability Prediction Model for Web Service Based on Binding Graph［J］. Computer Engineering,2015,41(5):14-18,25.