结合稀疏编码模型的多帧图像超分辨率重建

卢 健,孙 怡

(大连理工大学信息与通信工程学院,辽宁大连116024)

结合稀疏编码模型的多帧图像超分辨率重建

卢 健,孙 怡

(大连理工大学信息与通信工程学院,辽宁大连116024)

传统序列超分辨率方法对低分辨率视频序列的要求较高,一旦序列中没有包含足够的信息,会造成重建高分辨率图像质量的下降。为此,提出一种结合稀疏编码模型的序列超分辨率算法。利用概率运动场从低分辨率序列中重建一幅高分辨率图像,根据自适应阈值确定重建有效和无效区域,使用稀疏编码模型对无效区域进行补全重建。实验结果表明,该算法可以采用序列自身的信息和稀疏字典中的信息来重建高分辨率图像,在序列信息有破缺时,与仅利用序列自身信息或仅利用单幅图像的算法相比,具有更好的鲁棒性和广泛的适用性。

超分辨率;稀疏编码;图像补全;非局部正则化;线性反问题

1 概述

超分辨率(Super-resolution,SR)重建是一种突破成像硬件限制提高图像质量的算法。从广义上分,主要包括:(1)多帧超分辨率;(2)单幅图像超分辨率。多帧超分辨率能够利用连续多帧低分辨(Low-resolution,LR)图像中不同而又相似的信息,重建高于成像系统分辨率的图像,也被称作序列超分辨率。经典的序列超分辨率算法,包括最大似然法、最大后验概率法、凸集投影法以及后向投影迭代法等［1］。由于序列超分辨率包括配准和重建2个阶段,近年来一些新的思路不断被引进分别用来解决这两方面的问题。在配准方面,文献［2］尝试使用互信息来提高配准精度,文献［3］利用各项异性扩散方程来提高配准可靠性,而文献［4］则引入尺度不变特征变换(Scale Invariant Feature Transform,SIFT)特征点实现跨尺度配准。与追求准确性相反,文献［5］利用非局部核回归实现了不需要精确配准的超分辨率算法。在重建方面,文献［6-7］分别利用差值曲率和形态学对图像进行度量,并利用度量结果对总变分(Total Variation,TV)正则项进行加权,从而提高了正则项的自适应性。此外,为了避免不同阶段误差的累积,能够同时对配准和重建参数进行估计的联合最大后验概率(Maximum a Posterior,MAP)算法［8］也被提出。尽管各种算法各有侧重,但序列超分辨率都依赖同样的假设,即序列中需要存在足够的信息,一旦信息破缺,则会造成重建质量的下降。

而单幅图像超分辨率则需要从外部样本库中学习获得先验知识来重建图像的高频细节。为了解决样本库过大的问题,近年来,许多最新的信号表示手段被引入到单幅超分辨率的领域。如文献［9］将流形学习的算法引入超分辨率,文献［10-11］则利用稀疏字典来实现超分辨率重建。

综上,序列和单幅图像超分辨率各有优势与不足。视频序列通常是对同一场景的连续拍摄,帧间相关性强,多帧超分辨率直接利用这些相关信息进行高分辨重建,因此,重建的高频信息更加准确。然而,由于实际拍摄过程往往存在大量不可控因素,如拍摄对象运动过快、物体的遮挡等,这些因素破坏了序列中信息的完整性,通常会在重建结果中形成明显的干扰物。而单幅图像超分辨率重建,可从样本库中获取额外的信息,避免了序列超分辨率中由于信息破缺而导致的重建质量下降问题,因此重建结果更加鲁棒。然而,由于样本库中的样本通常与所要重建的图像相关性较弱,从而重建的高频信息往往不够准确,这也是单幅超分辨率常被称作“幻像”［12］的原因。长期以来,2类算法在各自的领域不断发展,然而结合两者优势的超分辨率研究相对较少,其原因在于难于度量哪些区域适合从序列中提取信息,而哪些区域适合从外部的样本中获取信息。

为解决上述问题,本文在序列超分辨率的基础上,推导出自适应阈值对重建图像进行度量,从而确定不适合序列重建的无效区域,然后采用稀疏模型对该区域进行补全重建。

2 基于概率运动场的超分辨率重建

建立观测模型是研究超分辨率重建的前提。在实际的成像过程中,降质因素主要包括模糊,帧间运动下的采样及噪声,其模型可用下式表示:

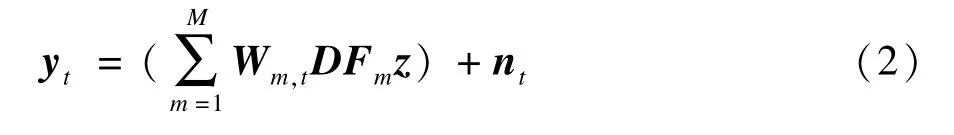
由于Ft需要从降质的低分辨序列中估计获得,因此估计准确度较低,而估计误差常常会造成重建质量的严重下降。针对这一问题,文献［13］提出一种新的基于概率运动场的观测模型:其中,矢量z=Hx表示模糊的高分辨图像。假设像素在水平和竖直方向的最大移动范围为d个像素,则每一个像素最多会有M=(2d+1)2种可能的移动方式,Fm表示第m种移动方式的矩阵,而像素最终进行的运动则由权重矩阵Wm,t来描述。Wm,t是一个对角阵,其对角元表示第t帧图像上对应像素进行了第Fm种位移(即［dx(m),dy(m)］)的可能性大小,如果某一像素进行了第Fm种位移的可能性较大,则相应的对角元接近于1,否则,接近于0。在文献［13］中,这种由可能性权重描述的运动估计模型被称为概率运动场。概率运动场的超分辨率模型,将原本一个像素只能有一种可能运动的问题转换为一个像素可以有多种可能运动的问题,从而避免了算法对单一运动估计准确性的依赖。

在建立了概率运动场超分辨率观测模型之后,重建问题即是式(2)的反问题,该问题需要使用最大似然估计来优化求解:

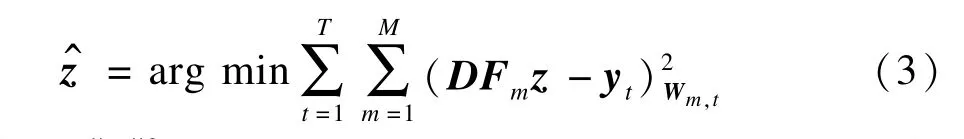
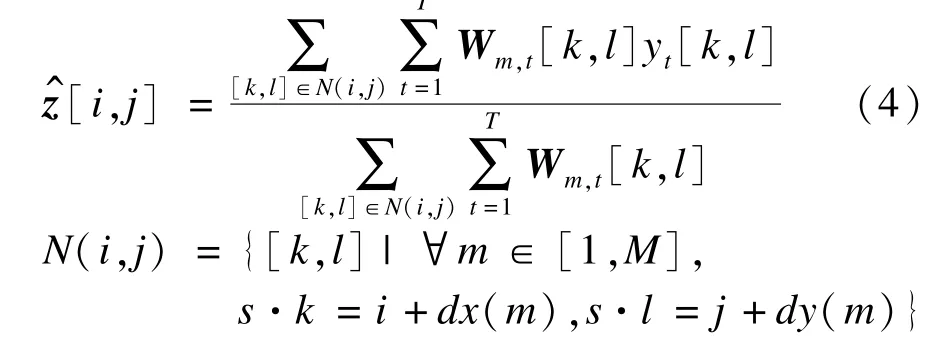
其中,［i,j］表示高分辨图像上的像素坐标;N(i,j)表示低分辨图像上的像素集合;集合中坐标为［k,l］的像素经过第Fm种移动后,可以融合到高分辨率图像的第［i,j］点上。

3 概率运动场权重计算与无效区域确定

由式(4)可见,概率运动场超分辨率算法的关键在于能否有效地估计出运动场权重Wm,t［k,l］,即第t帧低分辨图像［k,l］位置上的像素做第Fm种运动的可能性大小。文献［13］使用像素所在邻域平方误差(Sum of Squared Difference,SSD)的e指数来计算权重,具体表示如下:

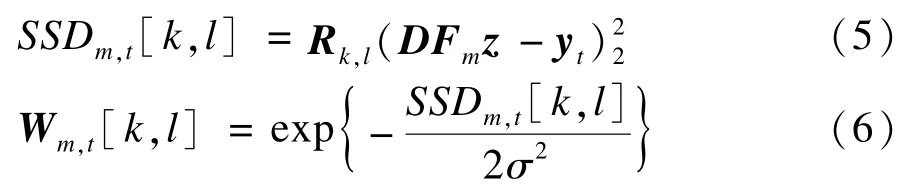
其中,Rk,l表示取邻域算子矩阵。SSDm,t较大说明高分辨图像上某一像素经第Fm种移动后其所在邻域下采样与第t帧低分辨率图像上相应像素所在邻域差异较大。由此可知,如果将低分辨图像上的相应像素,按照Fm的运动形式融合到高分辨图像中,会造成该点与其邻域的显著差异,因此,为了避免这些“异常点”对重建的影响,应当令其权重Wm,t为0。然而exp(·)只有在SSDm,t非常大的情况下才能够将权重映射为0,因此,按照式(6)计算权重会使得相当一部分“异常”点仍然有可能参与到重建过程。剔除这些SSD较大的异常点,最简单的办法就是进行一个硬阈值滤波,但是如图1所示,由位移造成的SSD差异与像素所在邻域图像有关。由位移造成的不同邻域块的 SSD如图1所示,其中,图1(a)、图1(b)的SSD为1.87;图1(c)、图1(d)的SSD为28.16。图1(b)和图 1(d)分别是将图1(a)和图1(c)向右移动一个像素所得到的邻域块,虽然位移相同,但是图1(a)和图1(b)与图1(c)和图1(d)各自的SSD却显著不同,邻域变化较缓的,产生的差异较小,而邻域变化较大的,产生的差异也较大。因此,很难给出一个统一的阈值,为此,本文提出一种能够根据邻域内容自适应地计算阈值的算法。

图1 位移造成的不同邻域块的SSD对比

由超分辨率原理［1］可知,只有相互存在亚像素级位移的低分辨图块才能保留下互补的信息,从而重构出高分辨图块。因此,SSD阈值可以通过求取像素所在邻域图块经过亚像素级位移后可能产生的最大SSD来确定。如果令矢量A=DFmz,矢量B=yt,则式(5)可表示为:

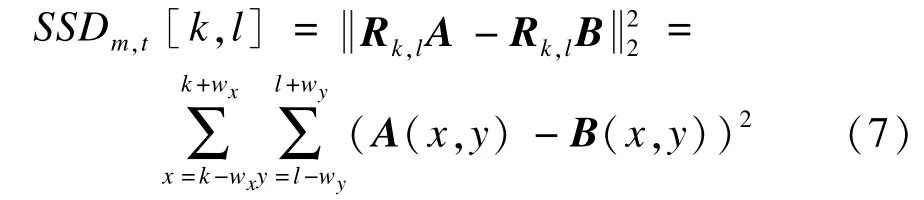
其中,邻域尺寸为(2wx+1)×(2wy+1)。假定A与B之间存在亚像素位移d—=［dx,dy］T,即:

B(x,y)=A(x+dx,y+dy)

则式(7)可进一步表示为:

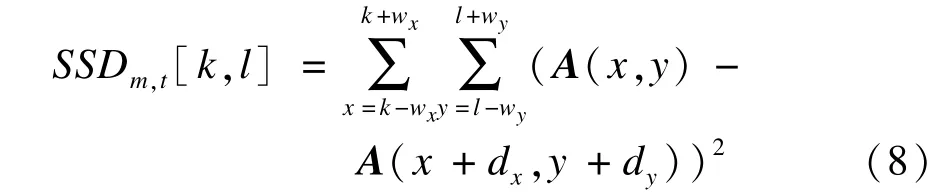
由于［dx,dy］T很小,因此可用一阶Taylor展开来逼近,由此可得:

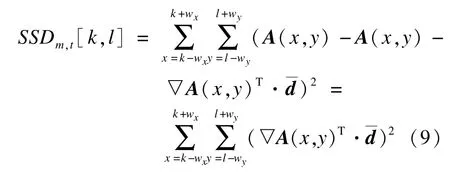
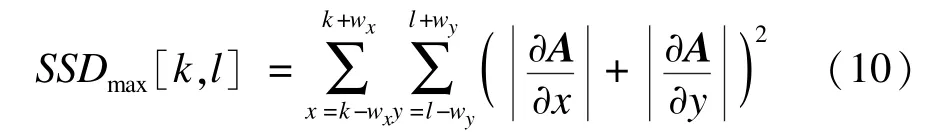
如果2个邻域图块之间的SSD超过上式值,则表明2个邻域之间不足够“相似”(超出了亚像素的位移),即没有可以互补的信息了。通过以上分析,可将剔除异常点的自适应阈值设置为:

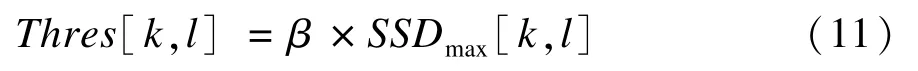
其中,β为常数,作用是调节阈值的严格程度。在本文实验中β=1便可以取得不错的效果。

由式(10)可知,阈值与邻域自身的梯度变化有关,梯度变化大的,相应的阈值也较大,这与图1所示实验的结果一致。在对每个像素点求得阈值之后,便可对异常点进行滤除,即令其权重为0:

在获得了运动场权重之后,便可利用式(4)进行超分辨率重建。图2(a)展示了对Foreman视频的重建结果,图中黑点是无效区域,即用来重建该点的像素权重均为0。图2(b)是对重建有效区域与无效区域的划分,黑色代表无效区域,白色代表有效区域。从划分结果可以看出,无效区域主要有2种类型:(1)平坦区域,如墙板、帽盔等处,这主要是因为平坦区域自适应SSD阈值较小,噪声干扰很容易造成该区域内点的SSD超过阈值,导致权重为0,不过,平坦区域变化规律简单,因此,比较容易补全重建;(2)运动过快的区域,比如嘴部,该区域由于运动过快,前后帧中没有保留下太多相关的信息,因此,也无法从序列中提取出足够有效的信息进行重建。

图2 重建结果与有效/无效区域

由上述分析可以看出,本文提出的自适应阈值可以有效地筛选出重建图像中不适宜从序列本身提取信息进行重建的区域,对于这部分区域,将会继续利用外部的样本库对其进行重建。

4 基于稀疏编码模型的无效区域重建

基于学习的算法通常用于单幅图像超分辨率。该类算法通过对样本的学习获取高低分辨率图像之间的先验知识,以指导高分辨率图像的重建。但传统算法常受困于样本库过大的问题,文献［10-11］将稀疏表示的理论引入到超分辨率领域,通过稀疏学习,将样本库整理成为更为紧致的稀疏字典,提高了基于学习算法的效率。针对所要解决的问题,本文提出一种通过字典对重建图像有效区域内的信息进行稀疏编码,从而重建无效区域的算法。

4.1 加权稀疏编码模型

建立该问题的稀疏编码模型:

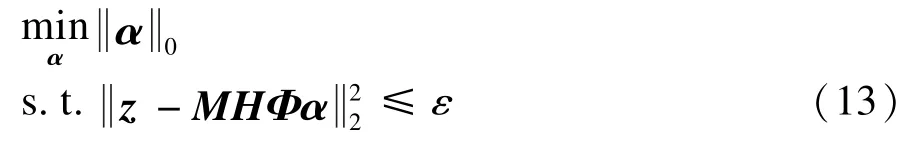
其中,矢量z∈RN×1为由序列重建出的模糊超分辨率图像;M为遮罩对角阵,对角元为1表示对应像素属于有效区,为0表示其属于无效区域;H为模糊矩阵;矩阵Φ∈RN×L表示稀疏字典;矢量α∈RL×1为稀疏系数,为α中非零元个数,表示α的稀疏度; ε为误差容限。该模型的意义在于,对重建图像进行稀疏编码,使得通过编码重建后的图像在有效区内与序列重建结果保持一致,而在无效区内根据稀疏约束,在字典中选择合适的样本对其进行重建,通过求解上述优化问题,可得稀疏编码矢量α^,最终高分辨率图像矢量x即可由下式重建:

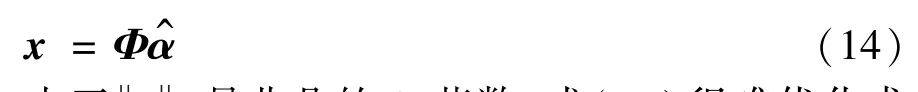
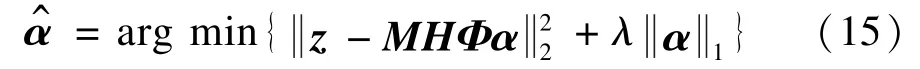
其中,λ是一常数,表示稀疏约束的强度。文献［14］指出加权l1范数能够更有效地逼近l0范数,提高重建质量,并给出了一种权重取值算法,是αi的估计值,ξ为小常数。该加权的意义在于对接近于0的系数给予更大的惩罚,使其变为0,从而提高系数的稀疏性。通过引入加权l1范数,可进一步获得加权稀疏编码模型:

4.2 非局部正则化

上述稀疏模型主要考虑了图像局部的稀疏性。而近年来,许多研究表明自然图像上会有大量相似模式重复出现,这种现象被称作非局部相似性。许多利用非局部相似性进行的研究都取得了不错的结果［5,10-11］。作为对局部稀疏性的一个补充,本文进一步将非局部正则化算法引入到重建模型中。

首先,以高分辨图像上每一像素xi为中心,提取n×n大小的邻域N(xi),然后在整幅图像中(实际应用中可确定一个适当的搜索范围)利用最近邻的方式搜索前K个最相似的邻域为每个邻域的中心像素。

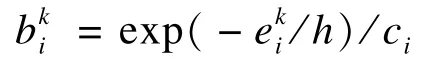
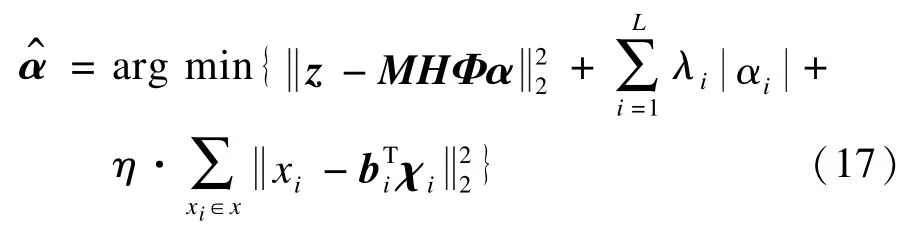
其中,η为控制常数,用来控制非局部正则约束的强度。加入非局部正则化的稀疏编码模型在保证了重建图像局部稀疏性的同时,也保证了图像的非局部相似性。式(17)还可以进一步表示为:

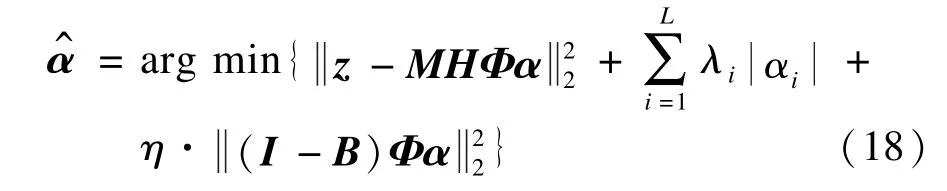
其中,I为单位矩阵;矩阵 B中的元素可由下式给出:

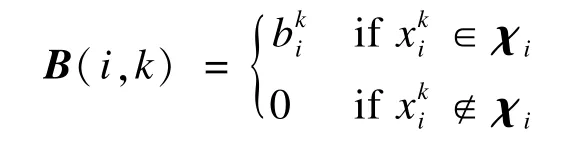
5 算法描述

式(18)可以进一步整理成下式:

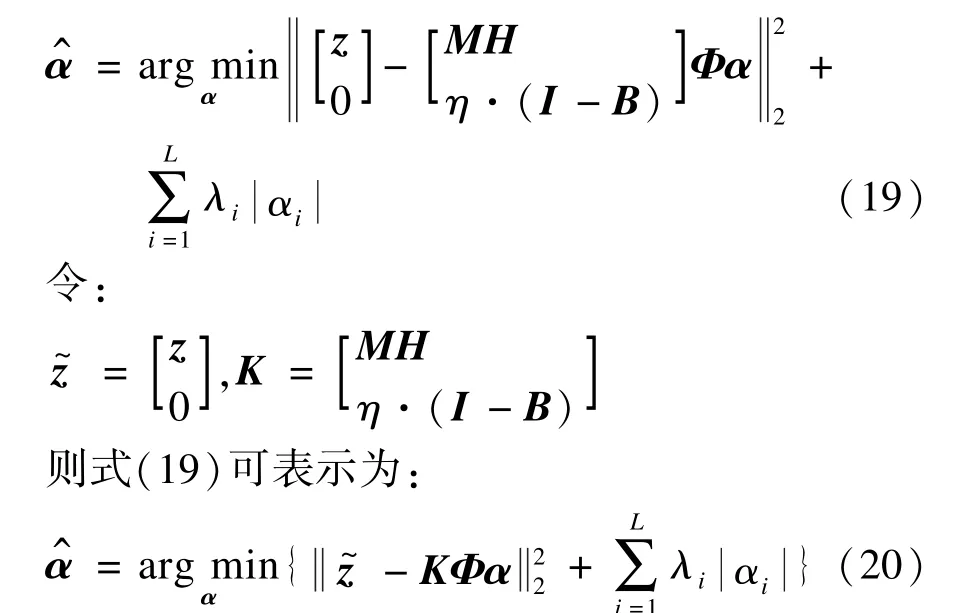
由此可以看出这是一个加权l1范数的线性反问题,该问题可以利用迭代收缩算法［15］进行求解。本文超分辨率算法求解过程如下:

(1)序列重建

1)用式(6)构造输入视频序列的概率运动场。

2)用式(10)和式(12)计算阈值,对运动场权重进行自适应硬阈值滤波。

3)用式(4)从序列中重建高分辨率图像矢量z,同时利用得到的有效/无效区域构造遮罩矩阵M。

4)利用z作为x的初始估计矢量x(0)(无效区域利用插值填补),同时利用x(0)计算矢量bi构造非局部权重矩阵B。

5)设定相关参数η,P,e,最大迭代次数Max_Iter。

(2)稀疏模型迭代重建

1)利用迭代收缩算法对高分辨图像矢量x进行求解,迭代公式如下:

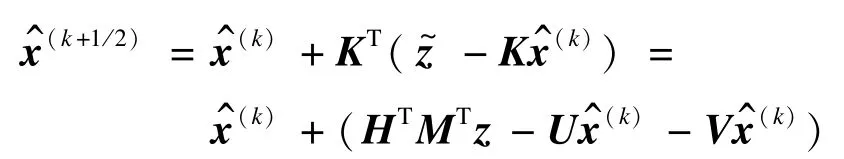
其中,U=(MH)TMH,V=η2(I-B)T(I-B)。

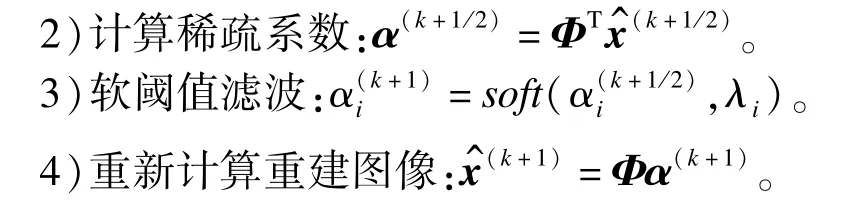
5)每隔P次迭代,利用最新重建的图像重新估计局部权重阵B,当或k＞Max_Iter,迭代终止。

软阈值函数具体形式为:

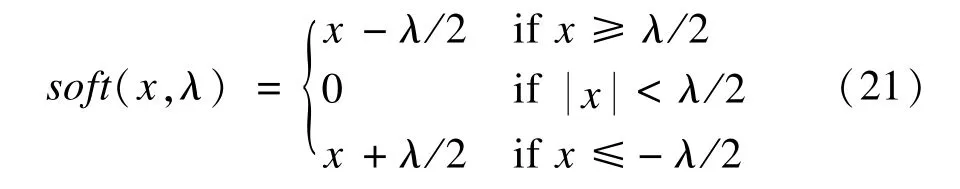
6 实验结果与分析

为验证算法性能,本文采用实际视频序列进行重建实验,通过比较本文算法和其他算法的重建结果,来验证算法的有效性。本文采用的比较算法包括序列超分辨率算法和单幅超分辨率算法。序列超分辨率算法是基于概率运动场的算法(Probabilistic Motion Based Super Resolution,PMSR)［13］,单幅超分辨率是基于非局部中心化稀疏的算法(Nonlocally Centralized Sparse Representation,NCSR)［11］。

所有实验如未做说明均采用相同的实验参数,其中,η=0.04,β=1,计算权重时的邻域尺寸为7× 7像素。所用字典Φ是由K-SVD算法［16］从由15幅自然图像构成的样本库中学习获得的。样本库的构造过程为,首先将15幅图像分割成7×7像素大小的图像块,然后从这些图像块中随机选取100 000块作为训练样本。考虑到计算复杂度和重建质量,将训练后的字典中的原子数目设置为1 024。以下所有实验均采用同一个字典。除了主观评价之外,本文还采用峰值信噪比(Peak Signal-to-Noise Ratio, PSNR)对重建图像质量进行了客观评价。

首先,本文从标准CIF视频序列中选择了Suzie和Foreman 2个具有代表性的序列进行实验。Suzie中有头发等细节部分,可以检验算法对细节重建的能力,而Foreman嘴部动态变化较快,可以检验算法在序列中有效信息破缺时的重建能力。实验分别从上述2个视频中截取连续30帧图像,经模糊、下采样以及加噪处理后,生成低分辨图像序列,其中,模糊核为3×3的均匀模糊核,下采样因子为3,噪声为标准差等于2的高斯白噪声,然后分别用前述2种算法和本文算法对2个序列进行重构。

图3展示了Suzie视频第8帧的重建结果,其中,各子图的下半部分是重建结果的细节放大图,图3(a)中的方框标明了放大细节在原图中的位置。从结果中可以看出,当序列中存在较多可用信息时,基于序列重建的算法可以获得很好的重建结果,比如图3(b)中眼睛、电话等处,而当序列中没有较多可用信息时,序列重建的算法便无法获得很好的结果,比如Suzie的头发处不够清晰。相反,基于学习的算法图3(b),能够从样本库获取知识,对头发处重建效果较好,但是由于样本库中的信息与要重建的图像之间相关性较弱,加上噪声和下采样混叠的干扰,导致眼睛和电话等处重建结果并不理想。而本文算法由于能够结合2种算法的优点,因此,在各细节处都取得了不错的重建效果。

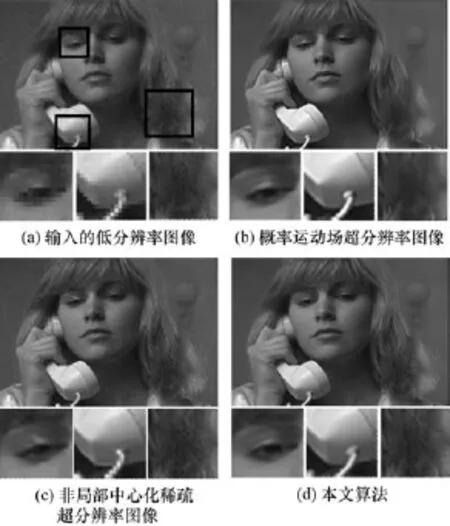
图3 Suzie序列重建结果

图4 展示了Foreman视频第22帧的重建结果。图中各子图的下半部分是重建结果的细节放大图,图4(a)中的方框标明了放大细节在原图中的位置。由于Foreman嘴部运动过快,导致视频前后帧关于嘴部的相关的信息严重不足。因此,基于序列的算法在重建结果,如图4(b)中,出现了杂点现象。而基于学习的算法利用样本库中的信息较好地恢复了嘴部信息。但由于严重的下采样混叠影响了样本选择,导致混叠信息在重建的结果中仍然存,如图4(c)中的墙板处。而本文算法可以利用序列中的相关信息来减少混叠,同时,对于序列中破缺的信息,还可以利用稀疏模型进行重建,因此,在嘴部和墙板处能够取得较好的重建结果。

图4 Foreman序列重建结果

表1给出了上述2个实验中重建视频30帧的平均PSNR评测结果。此外,为了进一步检测算法的广泛适用性及鲁棒性,本文继续从标准的CIF视频库中,选取了另外6段视频进行了如上所述的重建实验,然后对各重建视频序列求其平均PSNR指标。从评测结果可以看出,相较于其他2种算法,本文算法对不同的视频内容几乎都可以取得较好的重建结果。这进一步说明本文算法具有广泛的适用性和鲁棒性,可以有效地提高序列超分辨率在实际应用中的重建质量。

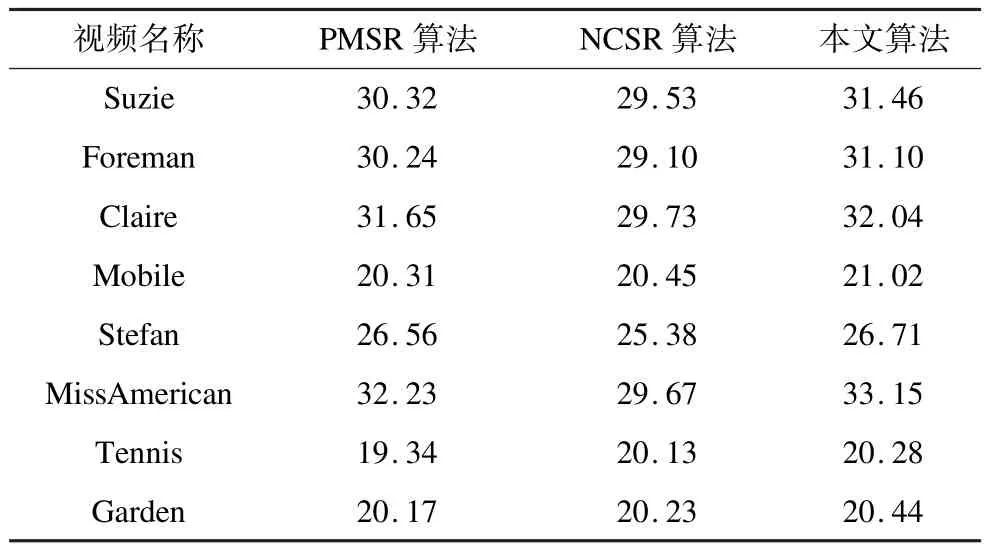
表1 超分辨率重建结果的PSNR dB

表2给出了上述8组实验在同一机器上重建一帧需要的平均时间。机器的配置为 Intel Pentium 2.7 GHz双核处理器,计算工具为Matlab R2013a。从表中可以看出,本文算法需要在序列超分辨率之后,继续使用稀疏字典对无效区域进行重建,这大大增加了算法的执行时间。因此,在一些需要实时重建的应用场合,本文算法存在一定的局限性。

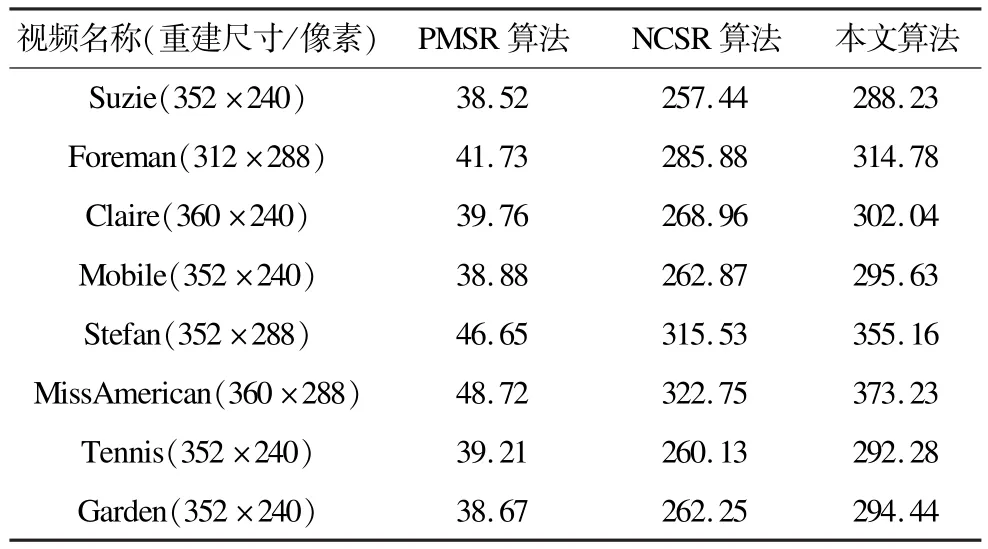
表2 超分辨率重建平均时间 s

7 结束语

受客观条件的限制,实际拍摄的视频无法满足理想超分辨率条件,存在不同程度的信息缺失。针对这一问题,本文提出一种自适应阈值算法,有效地区分序列重建的有效和无效区域,对无效区域,提出基于局部和非局部正则化的稀疏模型算法进行重建。实验结果证明了其有效性。然而,由于在序列超分辨率之后,该算法需要再应用稀疏字典对无效区域进行重建,这增加了算法的执行时间,因此如何进一步提高算法的效率将是今后的研究重点。

［1］卓 力,王素玉,李晓光.图像/视频的超分辨率复原［M］.北京:人民邮电出版社,2011.

［2］Vrigkas M,Nikou C,KondiL P.AccurateImage Registration for MAP Image Super-resolution［J］.Signal Processing:Image Communication,2013,28(5):494-508.

［3］Lu Jian,Zhang Hongran,Sun Yi.Video Super Resolution Based on Non-localRegularization and Reliable Motion Estimation［J］.Signal Processing: Image Communication,2014,29(29):514-529.

［4］李 展,张庆丰,孟小华,等.多分辨率图像序列的超分辨率重建［J］.自动化学报,2012,38(11):1804-1814.

［5］Zhang Haichao,Yang Jianchao,Zhang Yanning,et al. Image and Video Restorations via Nonlocal Kernel Regression［J］.IEEE Transactions on Cybernetics, 2013,43(3):1035-1046.

［6］Yuan Qiangqiang,Zhang Liangpei,Shen Huanfeng. Multiframe Super-resolution Employing a Spatially Weighted Total Variation Model［J］.IEEE Transactions on Circuits and Systems for Video Technology,2012, 22(3):379-392.

［7］Purkait P,Chanda B.Morphologic Gain-controlled Regularization for Edge-preserving Super-resolution Image Reconstruction［J］.Signal,Image and Video Processing, 2013,7(5):925-938.

［8］Liu Ce,Sun Deqing.On Bayesian Adaptive Video Super Resolution［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence,2014,36(2):346-360.

［9］Su Heng,Jiang Nan,Wu Ying,et al.Single Image Super-resolution Based on Space Structure Learning［J］. Pattern Recognition Letters,2013,34(16):2094-2101.

［10］Dong Weisheng,Zhang Lei,Shi Guangming,et al.Image Deblurring and Super-resolution by Adaptive Sparse Domain Selection and Adaptive Regularization［J］.IEEE Transactionson ImageProcessing,2011,20(7): 1838-1857.

［11］Dong Weisheng,Zhang Lei,Shi Guangming,et al. Nonlocally Centralized Sparse Representation for Image Restoration ［J］. IEEE Transactions on Image Processing,2013,22(4):1620-1630.

［12］Freeman W T,Jones T R,Pasztor E C.Example-based Super-resolution［J］.IEEE Computer Graphics and Applications,2002,22(2):56-65.

［13］Protter M,Elad M.Super Resolution with Probabilistic Motion Estimation［J］.IEEE Transactions on Image Processing,2009,18(8):1899-1904.

［14］Candes E J,Wakin M B,Boyd S P.Enhancing Sparsity by Reweighted L1 Minimization［J］.Journal of Fourier Analysis and Applications,2008,14(5/6):877-905.

［15］Daubechies I,Defrise M,De M C.An Iterative Thresholding Algorithm for Linear Inverse Problems with a Sparsity Constraint［J］.Communications on Pure and Applied Mathematics,2004,57(11):1413-1457.

［16］Aharon M,Elad M,Bruckstein A.K-SVD:An Algorithm for Designing Overcomplete Dictionaries for Sparse Representation［J］.IEEE Transactions on Signal Processing,2006,54(11):4311-4322.

编辑 刘 冰

Multi-frame Image Super-resolution Reconstruction Combined with Sparse Coding Model

LU Jian,SUN Yi
(School of Information and Communication Engineering,Dalian University of Technology,Dalian 116024,China)

Classic multi-frame Super-resolution(SR)techniques strongly rely on the supportability of Low-resolution (LR)frames.When the frames contain insufficient information,annoying artifacts often appear in the SR outcome.To solve this problem,a multi-frame SR combined with sparse coding technique is proposed in this paper.A high-resolution frame is reconstructed by the help of probabilistic motion estimation,and meanwhile effective/ineffective regions can also be determined by using an adaptive threshold segment.A sparse-coding-based completion technique is applied to recover the ineffective regions.Experimental results show that the proposed algorithm can essentially exploit the information from both LR frames and sparse coding dictionary.Compared with SR methods which depend only on image sequence itself or a single frame,the proposed algorithm has better robustness and extensive applicability.

Super-resolution(SR);sparse coding;image completion;non-local regularization;linear inverse problem

1000-3428(2015)05-0264-06

A

TP391

10.3969/j.issn.1000-3428.2015.05.049

卢 健(1978-),男,博士研究生,主研方向:图像处理;孙 怡,教授。

2014-05-06

2014-07-03E-mail:lslwf@dlut.edu.cn

中文引用格式:卢 健,孙 怡.结合稀疏编码模型的多帧图像超分辨率重建算法［J］.计算机工程,2015,41(5):264-269,273.

英文引用格式:Lu Jian,Sun Yi.Multi-frame Image Super-resolution Reconstruction Combined with Sparse Coding Model［J］.Computer Engineering,2015,41(5):264-269,273.