纺织材料设计反问题的贝叶斯统计推断方法
何炎高, 徐定华, 陈瑞林
(1. 浙江省服装工程技术中心(浙江理工大学), 浙江 杭州 310018; 2. 浙江理工大学 理学院, 浙江 杭州 310018)
纺织材料设计反问题的贝叶斯统计推断方法
何炎高1,2, 徐定华1,2, 陈瑞林1,2
(1. 浙江省服装工程技术中心(浙江理工大学), 浙江 杭州 310018; 2. 浙江理工大学 理学院, 浙江 杭州 310018)
针对具有不适定性纺织材料设计反问题,给出了利用贝叶斯蒙特卡洛方法求解纺织材料单参数和多参数反演问题的一种新方法。因织物稳态热湿传递模型的非线性和反问题的不适定性,基于贝叶斯统计推断方法的纺织材料类型、厚度、孔隙率等参数的后验概率分布推断是一种有效的方法。这种方法将参数的先验信息描述为先验概率密度,构建了纺织材料设计反问题的数值算法。数值实验结果表明,与马尔科夫链蒙特卡洛抽样算法相匹配的贝叶斯推理可用来求解纺织材料设计反问题。
纺织材料; 设计; 反问题; 贝叶斯推断; 单参数; 多参数
随着人民生活质量的改善和科技水平的提高,纺织材料的功能和应用领域也不断增多,纺织服装的热湿舒适性要求也日益受到关注,因此,基于人体舒适性要求的纺织材料设计具有重要的现实意义。一般地说,在人体-服装-环境系统中,基于织物的热湿传递模型,根据热湿传递方程和初边值条件,给定织物的物理参数和结构参数,从而计算人体与织物间微气候区的温度或湿度,该问题被称为正问题(DP: direct problems)。根据服装的热湿舒适性要求来决定纺织材料的物理参数或结构参数,该问题被称为反问题(IP: inverse problems)。通常由于测量数据有限且带有一定的误差,使得反问题具有不适定性,因而在求解时存在较大的困难,针对其不适定性问题,常见的反演方法有正则化方法, 此时往往转化为最优化问题进行参数估计,如 Hooke-Jevees模式搜索算法[1]、0.618法、或粒子群算法[2]来求解。近期建立在统计学基础上的贝叶斯推理在污染源识别反问题[4]、热传导反问题[5]、热辐射源估计[6]、热参数的估计[7]等研究中发挥了重要的作用并可较好地对反问题进行求解。
目前,纺织材料设计反问题研究尚处于初步阶段,本文针对织物稳态热湿传递反问题建立了贝叶斯推理的反演算法,采用马尔科夫链蒙特卡洛抽样的方法对后验状态空间进行抽样并获得了纺织材料参数的后验概率分布规律及进行相应的估计,可为纺织材料产品设计或实际生产提供理论参考和实践指导。
1 纺织材料热湿传递模型及反问题
在如图1所示的人体-服装-环境系统示意图中,考虑其平行圆柱孔的单层织物的稳态热湿传递模型[8-9]为
(1)
其初边值条件为
(2)
式中:k1和k2均为与水分子质量和气体常数相关的常数;ε(x)为纺织品表面孔隙率,%;r(x)为纤维孔半径,m;τ(x)为纤维孔的曲折系数;pv(x)为水蒸气压力,Pa;T(x)为织物温度,K;mv(x)为水蒸气质量通量,kg/(m2·s);Γ(x)为水蒸气凝结率,kg/(m3·s);λ为水蒸气吸收凝结热,J/kg;κ为织物的热传导系,W/(m·K);T(0)为织物内侧温度;T(L)为织物外侧温度;mv(0)为织物内侧水蒸气质量通量;pv(0)为织物内侧水蒸气压力。

图1 人体-服装-环境系统示意图Fig.1 Schematic diagram of body-clothing- environment system
饱和水蒸气压力的经验公式为
求解上述带有初边值条件的耦合常微分方程组称为正问题(DP),由Banach不动点定理可以证明其解的存在性和唯一性[9]。
服装舒适性是纺织材料为满足人体生理需要所必备的性能,也是纺织材料设计的核心要求。一般认为人体皮肤与服装内侧间的微气候区内温度(32±1)℃、湿度(50±10)%、气流(25±15)cm/s为标准服装气候,即为热湿舒适性指标[9]。因此,在一定温度和湿度的环境下,根据服装的热湿舒适性要求,决定织物的物理参数(如热传导系数κ)和结构参数(如厚度L、孔隙率ε)称为纺织材料设计反问题(inverse problem of textile material design,IPTMD)。
单参数的决定:给定环境的温度和湿度,根据服装的热湿舒适性指标,设计织物的热传导系数κ、厚度L或孔隙率ε,分别称为类型决定、厚度决定或孔隙率决定。
多参数的决定:给定环境的温度和湿度,根据服装的热湿舒适性指标,设计织物的热传导系数κ、厚度L、孔隙率ε中2个或全部参数。
2 正问题和反问题的数值算法
2.1 正问题DP的数值解法
将微分方程组模型(1)与(2)解耦[1]得
其中
用有限差分法离散得到以下差分方程:
当i=2,…,N-1时,
当i=N时,
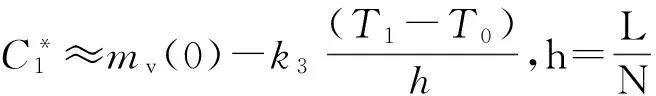
已知T0、TN,通过插值得到T1、TN-1,这样通过以上差分方程可以计算TN-2,…,T2,由此得到
进而微气候区的相对湿度(RH)的表达式可表示为
(3)
2.2 反问题IPTMD的贝叶斯推断方法
贝叶斯推理的基础是贝叶斯定理,即
(4)

从式(4)可以看出参数的所有信息都包含在后验分布中,一旦知道了后验概率密度函数的分布规律,就可以利用点估计的办法,如最大后验估计(MAP):
后验均值估计:
同样也可以作区间估计。
通常情况下,测量数据的边缘概率密度函数π(y)在后验状态空间中可看成积分常数没有进行计算的必要,因而后验概率密度函数可以简单地表示为

(5)
一般地,织物参数θi(i=1,2…m;m为模型参数的个数)在一定的范围θi∈[ai,bi]内且满足均匀分布,先验概率密度函数可表示为
(6)
由于各参数之间具有相互独立性,则总的先验分布可表示为
(7)
测量误差一般可以认为是白噪声η,其每个分量误差均服从均值为零、标准差为σ的正态分布N(0,σ2),似然函数可表示为
(8)
式中n为测量数据的个数。
从理论上讲,利用式(5)即可求出后验概率密度函数,但往往由于参数维数较大或正演关系比较复杂难以得到明确的数学表达式,使得数值积分算法计算量呈指数增长,因而计算难度较大,为此,需采用特定的抽样方法实现对后验概率密度进行求解。
2.3 马尔科夫链蒙特卡洛法
马尔科夫链蒙特卡洛(Markov Chain Monte Carlo,MCMC)法是一类算法的总称。从数学上讲,其思想是产生一个Markov链,以目标分布为平稳分布。根据Markov链理论,一个Markov链从任意初值出发,都会收敛到其平稳分布。MCMC就是用马尔科夫链的平稳分布,生成满足特定分布的随机数构造一个目标分布样本。
Metropolis算法[4]是一种重要的MCMC抽样算法,其算法可表述如下。
1)在模型参数先验范围内随机产生模型参数初始点θ(i),i=1;
式中π(θ*),π(θ(i))为目标概率密度函数。
3)产生一个0~1之间的随机数u;
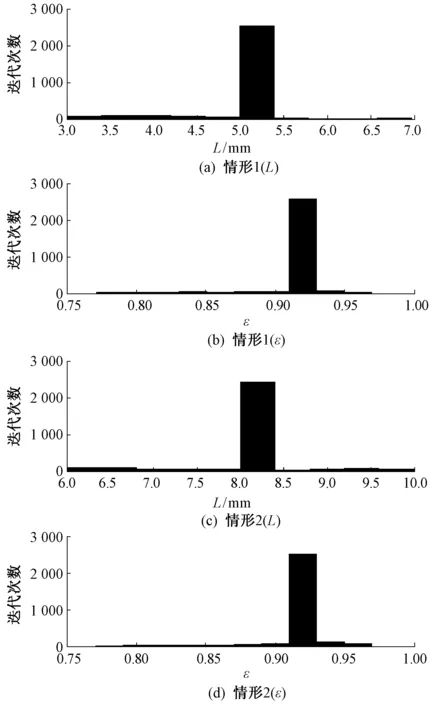
4)如果u 5)重复步骤3)、4)直到达到迭代次数。 利用马尔科夫蒙特卡洛方法对后验状态空间进行抽样,在大数法则的原理下根据样本均值依概率收敛性,可用收敛的样本均值去估计期望值[3]。 式中θ=(θ1,θ2,θ3),θ1=κ,θ2=L,θ3=ε。 在2种不同低温情形下进行数值实验, 微气候区o点作为观察点,观察数据源于2种情形下微气候区相对湿度的计算值(如图2所示),本文采用棉、羊毛、涤纶等常见的纺织材料或其混纺材料进行数值实验,相关参数及先验信息如表1所示,针对2种不同情形运用贝叶斯理论对反演参数进行后验均值估计。 图2 2种情形下微气候区内相对湿度的近似值Fig.2 Approximate RH in microclimate area at two cases.(a)Case 1; (b) Case 2 参数数值参数数值k/(W·(m·K)-1)0.1T(0)/K305.15ε0.9mv(0)/(kg·(m2·s)-1)3.083×10-5r/m1×10-5k16×10-5τ1.2k27×10-5λ/(J·kg-1)3.593×106RHe(0.4,0.9) 3.1 反演算例1:单参数κ或L的反演 针对情形1和情形2,待反演的模型参数为织物的热传导系数κ或厚度L。根据先验信息,待定参数的先验分布采用均匀分布,则其对应的先验概率密度函数分别为 数值实验模拟过程中假定观察误差服从白噪声N(0,σ2),σ=0.001,则似然函数条件概率密度分别为 根据贝叶斯定理及相应理论,织物的热传导系数和厚度后验概率密度函数分别为 式中,λ1、λ2为常数。 图3 情形1下参数κ反演结果Fig.3 Inversion results of parameter κ in case 1.(a) Iteration curve graph; (b) Posterior histogram 图4 情形2下参数L反演结果Fig.4 Inversion results of parameter L in Case 2.(a) Iteration curve graph; (b) Posterior histogram 3.2 反演算例2:参数(L,ε)同时反演 分别对2种情形下参数L和ε进行同时反演。根据先验信息,待反演模型参数先验分布采用均匀分布,其对应的先验概率密度函数为 数值实验模拟过程中假定观察误差η为白噪声N(0,σ2),σ=0.001,则似然函数条件概率密度可表示为 根据贝叶斯定理及相应理论,参数(L,ε)后验概率密度函数为 式中λ为常数。 图5 参数L和ε反演迭代曲线Fig.5 Iteration curves of parameters L and ε.(a) Case 1 (L); (b) Case 1(ε); (c) Case 2(L); (d) Case 2 (ε) 3.3 反演结果分析 从图3~5中可看出,迭代曲线开始具有一定周期振荡的特性,当迭代次数达到一定次数后趋于稳定状态,表明马尔科夫链进入稳定的收敛区域。从后验概率直方图可看出,单参数反演时,κ和L分别在0.1和0.008附近时的频数最大,与预设定值完全符合,参数的后验统计结果如表2所示。2种情形下参数L、ε同时反演时分别在0.005、0.9和0.008、0.9附近时的频数最大,与预设定值完全符合,参数的后验统计结果如表3所示。 图6 参数L和ε后验概率直方图Fig.6 Posterior histograms of parameters L and ε.(a) Case 1 (L); (b) Case 1 (ε); (c) Case 2 (L); (d) Case 2 (ε) 参数真值迭代次数后验均值估计均值误差/%κ0.110000.1030413.04L0.00810000.0080480.60 表3 L和ε的后验统计结果 结果表明,采用Bayesian-MCMC抽样算法的贝叶斯推理方法反演误差较小、精度较高。因而,可以利用反演结果对纺织材料类型选择和厚度设计进行理论指导,后验估计中可剔除前面没有达到平衡的点进行分析或进行参数反演时将Bayesian-MCMC方法与其他优化算法结合起来。在先验信息很少场合下,通常取无信息的先验分布,常用的有Reformulation方法、不变Haar测度方法、Box-Tiao技术、Lindley方法及最大熵原理。 本文针对纺织材料稳态热湿传递模型中的参数决定,建立了基于贝叶斯推断的反演数学模型及其数值算法,运用贝叶斯推断理论,提出了一种用Bayesian-MCMC方法决定纺织材料设计反问题的新方法。该方法可用来求解纺织材料热传导系数、厚度、空隙率等单参数或多参数设计反演问题。 Bayesian-MCMC方法是一种充分利用先验信息通过构造Markov链进行随机动态模拟,得到后验概率密度分布,具有估计精度较高,计算速度快等特点,针对复杂空间上多维估值问题,MCMC方法具有很强的适用性,同时求解比其他方法更容易。理论上,采用Bayesian-MCMC方法只要采样次数足够多,马尔科夫链一定收敛且可以精确得到后验分布。 [1] 徐定华,陈远波,程建新.低温环境下纺织材料类型设计反问题[J].纺织学报,2011,32(9):23-28. XU Dinghua, CHEN Yuanbo, CHENG Jianxin. Inverse problem of textile material design at low tempera-ture[J].Journal of Textile Research,2011,32(9):23-28. [2] CUI Peng, XU Dinghua. Simultaneous determination of thickness and heat conductivity in fabric design: steady-state modeling and PSO algorithms[J]. Journal of Fiber Bioengineering and Informatics,2013(2):195-204. [3] KAIPIO J,SOMERSALO E. Statistical and Computational Inverse Problems[M]. New York:Springer, 2004:91-108. [4] 陈海洋,腾彦国,王金生,等.基于Bayesian-MCMC方法的水体污染识别反问题[J].湖南大学学报:自然科学版,2012(6):74-78. CHEN Haiyang, TENG Yanguo, WANG Jinsheng, et al. Event source identification of water pollution based on Bayesian-MCMC[J]. Journal of Hunan University: Natural Science Edition, 2012(6):74-78. [5] WANG Jingbo, ZABARAS Nicholas.A Bayesian inference approach to the inverse heat conduction problem[J]. International Journal of Heat and Mass Transfer, 2004(47):3927-3914. [6] WANG Jingbo, ZABARAS Nicholas. Using Bayesian statistics in the estimation of heat source in radiation[J]. International Journal of Heat and Mass Transfer, 2005(48):15-29. [7] 高思云,杨晨.利用贝叶斯模型进行热参数估计[J].系统仿真学报,2006(6):1462-1465. GAO Siyun, YANG Chen. Bayesian model to parameter estimation[J].Journal of System Simulation, 2006(6): 1462-1465. [8] XU Dinghua, CHENG Jianxin, ZHOU Xiaohong. A model of heat and moisture transfer through parallel pore Textiles[J]. Proceedings of Textile Bioengineering and Informatics Symposium, 2010(5):1139-1144. [9] 徐定华. 纺织材料热湿传递数学模型及设计反问题[M].北京:科学出版社,2014:25-29. XU Dinghua. Mathematical Model of Heat and Moisture Transfer and Inverse Problems of Textile Material Design[M]. Beijing: Science Press, 2014:25-29. [10] XU Dinghua, GE Meibao.Thickness determination in textile meterial design:dynamic modeling and numerical algorithms[J]. Inverse Problems, 2012(28):035011. Bayesian statistical inference method for inverse problems of textile material design HE Yangao1,2, XU Dinghua1,2, CHEN Ruilin1,2 (1.EngineeringResearchCenterofClothingofZhejiangProvince(ZhejiangSci-TechUniversity),Hangzhou,Zhejiang310018,China; 2.SchoolofSciences,ZhejiangSci-TechUniversity,Hangzhou,Zhejiang310018,China) Aiming at the ill-posed of the inverse problem of textile material design(IPTMD), a new approach based on Bayesian Markov Chain Monte Carlo(Bayesian-MCMC) method was proposed for solving the problem of single and multiple parameter determination. Since the heat and moisture transfer model is non-linear and the IPTMD is ill-posed, it is proved that posterior distribution for the model parameters such as the heat conductivity, thickness and porosity of the material is an effective method. This method describes prior information of parameters as prior probability density, constructing numerical algorithms of the IPTMD. The numerical results show that Bayesian inference method agreed with Markov Chain Monte Carlo sampling algorithm can be applied to solve the IPTMD. textile material; design; inverse problem; Bayesian inference; single parameter; multiple parameters 10.13475/j.fzxb.201501002307 2013-11-25 2014-10-08 国家自然科学基金资助项目(11071221,11471287);浙江省高校重中之重纺织材料与工程一级学科和浙江省服装工程技术研究中心开放基金项目(2013KF10);浙江医学高等专科学校科研项目(2014XZA01) 何炎高(1985—),男,硕士生。主要研究方向为微分方程反问题的理论、计算及应用。徐定华,通信作者,E-mail:dhxu6708@zstu.edu.cn。 TS 101.1 A3 数值实验与结果分析









4 结 论

