确定性L系统在针织花型设计中的应用

张栋亚， 陈 莉， 王红菊

(1. 天津工业大学 纺织学院， 天津 300387； 2. 中国纺织信息中心， 北京 100025)



确定性L系统在针织花型设计中的应用

张栋亚1， 陈 莉1， 王红菊2

(1. 天津工业大学 纺织学院， 天津 300387； 2. 中国纺织信息中心， 北京 100025)

为拓展分形艺术在针织产品设计中的应用，对确定性L系统生成分形图的方法进行初步探索。采用VB编程，研究确定性L系统中单规则和多规则的算法，并通过变换算法中的参数，得到丰富多样的L系统图形。根据部分图形的自身特点，利用STOLL电脑横机M1花型设计系统进行花型设计，模拟织物真实效果，认为将确定性L系统生成的分形图形应用于针织花型设计是可行的。同时，通过拓宽多规则方法中的字符定义，还能生成二方连续性图案，这将有利于拓宽针织产品设计中的花型创意来源。

确定性L系统； 单规则； 多规则； 分形图形； 针织

分形艺术的产生给工业设计的实现带来了新生机，它是一种新的造型语言。通过计算机技术构造的分形图形既有节奏韵律、相似嵌套等传统美学特点，又有非线性动力系统的无穷玄妙美感[1]。L系统[2]是一种生成分形图形的重要方法，通过灵活改变参数和规则可以产生丰富多样的装饰图案，并且已经在纺织产品的图案设计[3-4]、组织设计[5-7]以及印花设计中得到研究和应用[8]。然而目前有关分形在针织产品设计中的探索，虽有涉及到经典M集图案在针织花型设计中的应用研究[9]，但较少注意到L系统这类分形图形生成方法的应用价值。因此，本文主要针对确定性L系统生成图形的算法进行研究，通过各种参数的变化，得到风格多样的精美图形，并将其应用到电脑横机上，试图为针织产品的花型设计提供新思路。

1 确定性L系统图形的生成原理

L系统是一种基于符号的并行重写系统[10]，将初始形式的每个字符按照给定的一组产生式规则依次进行替换，再对产生的字符串进行几何解释，即可生成图形。确定性L系统[11]是指每个字符都只对应一个产生式，其基本类型为D0L系统。

D0L 系统是一个有序的三元素集合G={V,ω,Pi(i=1, 2, …,k)}。其中：V是所有字符的集合；ω是初始的字符形式，称作公理；P是产生式的集合。产生式P通常写作a→x，对于任何字母a属于V，必须存在一个非空单词x，使a→x，其中x可以是a本身[2]。当i=1时，即D0L系统中只有一个产生式P1，称为单规则 D0L系统(本文简称为单规则L系统)；当i≥2时，称为多规则L系统[12]。

通常L系统采用“龟形图法”[11]解释生成图形，并常用以下符号：F表示向前移动一步，并画线；+表示逆时针旋转δ°；-表示顺时针旋转δ°；[表示将当前位置信息压栈；]表示将[时刻的信息出栈。在实际生成L系统分形图的过程中，符号的运用是可以灵活变化的[13]。

根据上述原理，通过VB编程即可生成确定性L系统图形，程序流程图如图1所示。首先选择确定性L系统分形图的生成算法，然后定义初始公理ω、替换规则P和变化角度δ等参数，迭代生成图形；并通过改变规则等各种参数，不断变化图形，当得到较为满意的图形时，将其保存为BMP图像。

图1 确定性L系统程序流程图Fig.1 Program flow diagram of deterministic L-systems

单规则L系统算法中只能包含一种画图字符，而多规则L系统算法中可以包含多种类型的字符：一种字符只用于被替换，而不用于绘图；另一种字符既能被替换，也能绘图。其中，绘图字符相应的图形解释可以相同也可以不同，因而多规则L系统的图形造型能力更为丰富。

本文为使替换规则P的表示尽量规范，规定小写字母字符(a、b)仅能替换，大写字母字符(A、B)既能替换又能绘图，且字符A画黑色的线段，字符B画灰色的线段。

通过修改ω、P、δ等各种参数，可以生成很多新颖奇特的图案造型，如表1和图2所示。图2(a)～(c)均只使用了一个规则，通过变化不同参数值(ω、P、δ)对应产生风格不同的图形。图2(d)～(e)分别使用了2种字符“A、a”和“A、B”的组合，虽然字符串都较简单，但图形结果均有鲜明层次。

表1 不同确定性L系统分形图对应的各项参数值

图2 表1中各项参数对应的图形Fig.2 Graphics corresponding to parameters in table 1.(a) Elegant pentagram; (b) Dynamic pentagram; (c) Flower clusters with branch; (d) Variability of snowflower; (e) Pane paper-cutting

2 确定性L系统图形的应用

通常针织CAD花型辅助设计系统可以选择导入图像，图像中的一个像素对应于一个针织线圈的位置。该线圈可以是由不同颜色的纱线组成，也可以是由不同组织的线圈结构组成。二者的区别是，在实际上机编织过程中，变换纱线容易实现，而变换结构既要考虑编织的可行性，又要考虑编织的效率，因此，在选定适宜针织花型的图形时，要根据图形自身特点进行合理设计。

例如，图2(a)作为花型的特点是轮廓个性鲜明，但中心缺乏细节内容，因而不适合用作大面积提花，考虑在细密的网眼地组织结构上变换平针结构，通过虚与实的对比表现出花型的轮廓纹理。图2(c)作为花型的特点是形象精巧且有序饱满，因而考虑搭配合适颜色的纱线进行双面提花即可。

通过STOLL电脑横机的M1花型辅助设计系统进行针织产品设计，并对针织物的实际效果进行模拟。图3为依据图2(a)、2(c)的花型特点设计的织物模拟视图。图 3(a)为网眼花型织物模拟视图，图3(b)为双色提花织物模拟视图。

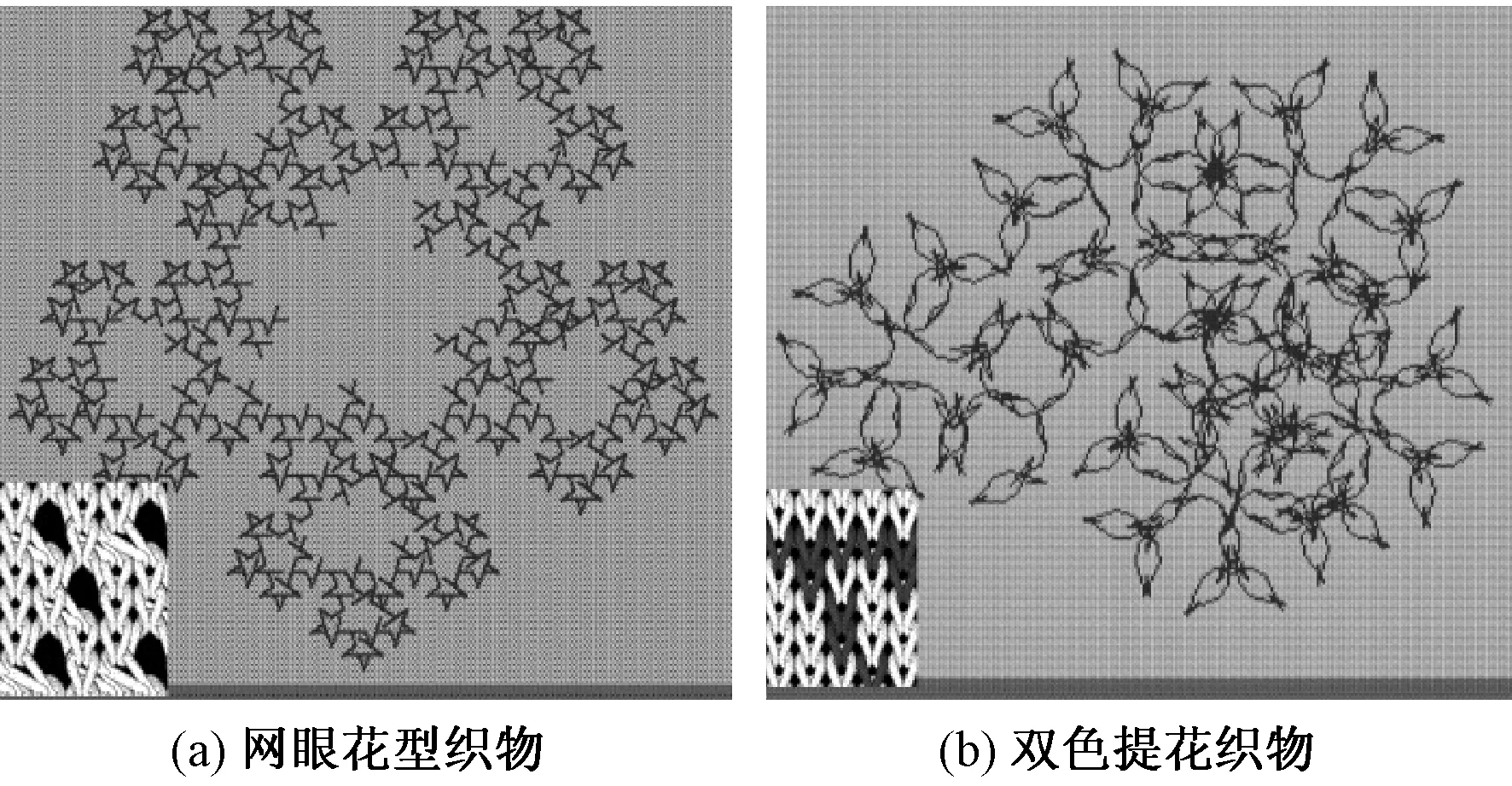
图3 织物模拟视图Fig.3 Knitted fabric simulation view.(a) Netting pattern; (b) Two-color jacquard knitted fabric

3 讨 论

根据L系统定义的规则迭代生成图形时，通常很难预料每次迭代的结果。随着迭代次数的增加，由于分形的自相似性，图形的整体造型可能变化不大，而且还可能导致细节混乱模糊。由此，通过分析总结大量L系统分形图的生成过程，得出获取有效图形时的迭代次数一般不超过8次。对于单规则L系统而言，虽然受到仅有一个画图字符的限制，但通过变化字符串的组合，并寻找合适的角度增量，仍能在迭代次数分别为1～5时观察到结构与特点完全不同的构图。对于多规则L系统而言，可定义的字符种类和数量增多，但相关影响图形的因素也随之增多，而且很难找到图形生成的一般规律或方法，因而也不适宜迭代次数过多。

一般在迭代1～ 3次时，相对容易发现一些较好的图形元素，该类图案面积小，可作为一个完全组织进行循环，形成一类常见的针织花型图案。

利用多规则L系统的造型能力，可以方便快捷地生成二方连续图案花型。当迭代到一定程度的图形已符合花型要求，则停止继续迭代，保存当前的结果字符串用字符“L”代替，作为新替换规则的一部分。再增加某种仅用于产生X轴方向或Y轴方向位移的字符(选用“X”或“Y”)，和控制图元向上或向下旋转角度的字符(选用“U”和“D”)，以及仅用于被替代，不产生位移，不用来绘图，只是为下次迭代产生图案埋下一颗种子的种子点字符[11](选用“M”)。由此，在新规则的情况下继续迭代时，将生成以上述不变图形为基本元素的二方连续图案，而且通过循环角度的变换，可以得到形态不同的连续排列方式。其中，循环角度是指字符“U”和“D”对应的角度值，主要控制循环图形元素的角度变化。

一般循环用的图形元素，可以由单规则生成，也可以由多规则生成，如图4所示。图4(a)、4(b)循环图元的相关参数如下。

初始公理：A角度为90°；迭代次数为2。

替换规则：A→A-A++A+A++A-A++A+A+。

循环规则：XXXU。

循环角度：图4(a)所示为0°；图4(b)所示为45°。

图4(c)、4(d)循环图元的相关参数如下。

初始公理：B角度为60°；迭代次数为3。

替换规则：P1，A→A++A++A。P2，B→B-A++A-B。

循环规则：XXXXU。

循环角度：图4(c)所示为175°；图4(d)所示为100°。

图4 二方连续图案Fig.4 Two sides pattern.(a) Structured lattices; (b) Jagged lattices; (c) Corrugated stars; (d) Striped stars

图4(a)、(b)和图4(c)、(d)的组成元素分别相同，但循环时的旋转角度不同，因而得到不同错落有致的效果。此外，若将循环规则中的“X”字符换为“Y”，还将形成竖直方向的二方连续图案。

4 结 语

确定性L系统生成的分形图形可以用来辅助针织产品的花型设计，而且花型模拟效果表现良好。这将有利于提升针织服装产品的市场竞争力和附加值。单规则L系统，通过改变初始公理、替换规则和角度等参数即可实现图形的多样化。多规则L系统相对内涵丰富，可以利用规则定义上的多重变化来扩展图形的造型能力。例如，目前已找到了一类生成二方连续图案的规律方法。因而，需要继续研究各种规则和参数对图形生成的影响，找到其他类型图形的生成特点和规律，这将成为探索分形L系统应用于针织产品设计的研究重点。

[1] 陈宁，刘道海. 分形与工业设计[J]. 艺术与设计，2012(89): 139-141. CHEN Ning, LIU Daohai. Fractal and industrial design[J].Art and Desgin,2012(89): 139-141.

[2] 齐东旭. 分形及其计算机生成[M]. 北京: 科学出版社, 1994: 32-47. QI Dongxu. Fractal and Computer-Generated[M].Beijing: Science Press, 1994： 32-47.

[3] 张聿，徐海宁. 基于L系统的简约主义风格家纺图案设计方法[J]. 艺术与设计, 2011(4): 225-227. ZHANG Yu, XU Haining. The methods of home textiles patterns design in simplisim style based on L-system graphics[J]. Art and Desgin,2011(4): 225-227.

[4] 杨旭红，李栋高，颜晓华，等. 基于分形L系统的纺织品图案的自动生成[J]. 纺织学报, 2003, 24(3): 193-195. YANG Xuhong, LI Donggao, YAN Xiaohua, et al. Automatic generation of textile pattern based on fractal L-system[J]. Journal of Textile Research,2003, 24(3): 193-195.

[5] 张聿，金耀，孙家武，等. 基于L系统的织物分形组织设计方法[J]. 纺织学报, 2007, 28(5): 51-54. ZHANG Yu, JIN Yao, SUN Jiawu, et al. Design method of fabric fractal weave based on L-system[J]. Journal of Textile Research, 2007, 28(5): 51-54.

[6] 张聿，岑科军，贾静静. 基于L系统的3×3平纹分形组织设计应用方法[J]. 纺织学报, 2011,32(11): 49-52. ZHANG Yu, CEN Kejun, JIA Jingjing. Design method of 3 × 3 plain fractal weave based on L-system[J]. Journal of Textile Research, 2011, 32(11): 49-52.

[7] 张聿，贾静静. 基于L系统的缎纹分形组织及其织纹效果设计[J]. 丝绸, 2011(5): 32-34. ZHANG Yu, JIA Jingjing. Method of designing fractal satin weave and its fabric texture based on L-system[J]. Journal of Silk, 2011(5): 32-34.

[8] 李琴，岑科军. 基于L系统的印花图案设计[J]. 丝绸, 2008(7): 12-13. Ll Qin, CEN Kejun. Studies on fabric printing-pattern design based on L-system[J].Journal of Silk,2008(7): 12-13.

[9] 陈莉,谢月凤. 基于逃逸时间算法的M集针织花型设计方法[J]. 纺织学报, 2010, 31(6): 62-65. CHEN Li, XIE Yuefeng. Method of designing knit pattern based on escape time algorithm Mandelbrot set[J]. Journal of Textile Research, 2010(6): 62-65.

[10] 孙博文. 分形算法与程序设计[M]. 北京: 科学出版社, 2004: 57. SUN Bowen. Fractal Algorithm and Programming[M]. Beijing: Science Press,2004:57.

[11] 靳润昭,王兆毅.L-系统的基本概念和示例[J].天津农学院学报, 2002,9(1):49-51. JIN Runzhao,WANG Zhaoyi. Essential concept of L-system and examples[J]. Journal of Tianjin Agricultural College,2002,9(1):49-51.

[12] 孟广利. L-系统分形图在纺织纹样设计上的应用[D].苏州:苏州大学,2012:19-23. MENG Guangli. Application of L-system to textile pattern design[D].Suzhou: Soochow University,2012:19-23.

[13] 丁灿剑，陈宇拓，韦冰，等. 基于L-系统的木雕图案的自动生成[J]. 电脑与信息技术, 2007, 15(1): 46-48. DING Canjian, CHEN Yutuo, WEI Bing, et al. Automatic generation of woodcarving patterns based on L-system[J]. Computer and Information Technology, 2007,15(1): 46-48.

Application of deterministic L-systems in knitting pattern design

ZHANG Dongya1, CHEN Li1, WANG Hongju2

(1.SchoolofTextiles,TianjinPolytechnicUniversity,Tianjin300387,China;2.ChinaTextileInformationCenter,Beijing100025,China)

To expand the application of fractal art in knitted product design, the method of generating fractal graphics based on deterministic L-systems was preliminarily researched. By programing with Visual Basic, single-formula algorithm and multi-formula algorithm of deterministic L-systems were studied. And a rich variety of graphics were generated by changing the parameters of the algorithm. Then some graphics were applied in pattern design based on their own characteristics, and the effects of knitted fabrics were simulated with M1 pattern design system of STOLL computerized flat knitting machine. The results indicated that these fractal graphics of deterministic L-systems are feasible to be the knitting patterns. At the same time, the two sides pattern could be created by broadening the definitions of the characters in multi-formula L-system. It will be conducive to broaden the creative pattern source of the knitting product design.

deterministic L-system; single-formula; multi-formula; fractal graphic; knitting

10.13475/j.fzxb.20140103004

2014-01-22

2014-10-08

张栋亚(1989—)，女，硕士生。主要研究方向为自动化针织产品设计。陈莉，通信作者，E-mail:clwsy@163.com。

TS 181.8

A