面向随机因素的多式联运动态路径优化
陈丹丹,洪 卫,贾 禹
(重庆交通大学 管理学院,重庆 400074)
面向随机因素的多式联运动态路径优化
陈丹丹,洪 卫,贾 禹
(重庆交通大学 管理学院,重庆 400074)
针对随机因素影响下多式联运所表现的动态性和随机性,在引入惩罚因子控制运输质量的基础上,以总费用最小化为目标,建立了具有软时间窗约束的动态路径优化模型;运用基于Dijkstra算法的改进路径优化算法求解模型;设计了一个基于铁路、公路、航空及水运等4种运输方式的多式联运问题的算例,验证了模型的实用性和有效性。
交通运输工程;多式联运;随机因素;动态路径优化;改进的Dijkstra算法
0 引 言
随着我国经济的迅猛发展,单一的货物运输方式已不能满足市场需求,人们越来越重视多式联运技术在国际货物运输领域的应用。与传统的运输方式相比多式联运具有高效、灵活、成本低、环保等特点,可降低运输成本,提高运输资源利用率以及企业竞争力。多式联运动态路径优化问题是目前多式联运技术研究的核心内容,具有十分重要的研究意义。
多式联运路径优化的研究中,V.R.Reddy,等[1]认为运输总费用由城市内中转费用和城市间运输费用组成,建立总费用最小的线性规划模型优化路径。A.Ziliaskopoulos,等[2]考虑多式联运过程中的时间因素,以运输时间最短前提建立模型求解。B.S.Boardman,等[3]以运输时间最短和成本最小为优化目标,进行路径优化。Tsung-sheng Chang[4]采用基于时间窗的多目标商品流模型解决多式联运路径选择问题,为多式联运路径优化中普遍关心的问题提供一种求解方法。魏航,等[5-6]考虑时变网络下多式联运的最短路径问题研究,采用标号法求解最短路问题。这些研究大多面向硬性的约束因素,以成本最小或运输时间最短为目标进行多式联运静态的路径优化。但是实际多式联运过程中易受交通、天气、机械故障等随机因素的影响,对运输过程中的运输时间,运输费用和运输质量也有较大影响。肖天国,等[7]结合运输时间与运输成本两个因素建立模型,并运用遗传算法求解联合运输路径优化问题。范志强,等[8]考虑运输过程中各节点的软时间窗约束问题,建立更加符合实际情况的多式联运路径优化模型。刘杰,等[9]考虑实际中航空、铁路、水运出发时间固定对路径选择的影响,提出各节点运输方式的备选集,建立多式联运动态路径优化模型。佟璐,等[10]研究多式联运路径优化模型与方法认为多式联运路径的选择受到运输成本、运输时间,运输质量和服务水平等相关因素的影响,将多式联运问题转化为一个最短路径优化问题。这些研究普遍针对随机因素影响下运输时间和运输费用两个因素建立模型,其中对各节点时间窗问题的研究已经取得一定成果。大多结合运输过程中的时间因素问题,把多式联运路径的动态路径优化转化为基于有限约束及总费用最小的最短路径问题,而随机因素影响下运输质量控制并没进行量化体现在优化模型中。
实际中,不同的运输路段运输费用、运输时间不同,航空、铁路、水运出发时间固定,货物损失,都是运输过程中随机因素影响的表现,也是多式联运动态路径优化不能忽略的因素。笔者综合考虑上述随机因素中的软时间窗约束和运输质量控制问题,以总费用最小为目标建立数学规划模型,并运用基于Dijkstra算法的改进路径优化算法求解,使多式联运的动态路径优化模型更符合实际情况。
1 问题描述及模型建立
1.1 问题描述
一般多式联运问题可描述为:某次物流作业需将货物从起点O运送至终点D,运输网络由N个节点组成,任意两节点间有K种交通方式可供选择。各运输方式的运输能力,运输时间,运输成本均不同。运输过程中各节点均可转换运输方式,运输方式转换便会产生中转时间和中转费用。
多式联运的实际问题中,铁路、水运、航空出发时间固定,运输货物要求在额定时间范围内到达各节点。如果货物早到,承运人则需等待,将会产生机会成本费用;如果晚到服务被延迟,可能产生多米诺效应,影响后面节点,应支付惩罚费用。模型中以到达终点时的货损率作为运输质量的衡量指标,并引入惩罚因子控制运输质量。若货物的货损率超过额定货损率,承运人应对货物进行赔付且受到相应惩罚。
1.2 模型建立
1.2.1 假设条件
1)假设运输路径由起点O到终点D,任意两节点间只能选择一种运输方式。
2)货物运输过程中,没有货物的增加或减少,货物运输量q恒定不变。
3)运输过程中的货损率和运输距离成正比,且与运输方式有关。
1.2.2 变量说明及模型
随机因素影响下的多式联运动态路径优化模型如下。
总费用由运输总费用、中转总费用、运输作业过程中提前到达节点的机会成本、运输作业过程中晚到节点的惩罚成本、作业提前到达终点的机会成本 、作业晚到终点的惩罚成本、终点出现货损时的赔付及惩罚成本构成,目标函数如式(1):

(1)
约束条件如下:
1)运输方式的选择约束,即在物流作业过程中两节点间只能选择一种运输方式:

(2)
2)在各节点中转时,只能中转到一种运输方式,且同一节点只能中转一次:

(3)
3)变量的逻辑约束:

(4)
4)各运输路段的运输能力约束,要求各路段能承载的货物量小于其额定值:

(5)
5)目标函数(1)中ti的表达式:

(6)
6)中转能力的约束:
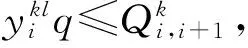
(7)
7)各节点前后运输方式对应约束,若在节点i采用运输方式k,则由节点i到节点i+1采用运输方式l:

(8)
8)货损率ws的计算表达式:
ws=srηr+sfηf+ssηs+saηa+ηt
(9)
9)变量的非负约束:
q≥0,ti≥0,PE>0,PL>0,P>0,Cw>0
(10)

2 求解算法
路径优化模型求解可看作是有限约束条件下的最短路径问题,笔者采用基于Dijkstra算法的改进路径优化算法即基于备选集的Dijkstra算法进行求解,刘杰[9]提到了该方法。基于备选集的Dijkstra算法是将运输网络中各节点的运输方式进行拆分,并排除其中不能中转或实际中不存在的中转方式,将各节点可行的运输方式形成备选集,然后在各节点选择路径时选择备选集中的可中转方式,从而找出最短路径。与传统的Dijkstra算法相比,改进后的方法能在各节点方便快捷的选择中转路径,避免求解过程中的成本浪费,节约求解时间,降低求解难度。
由于各运输方式的运输距离、时间及运输费用不同,求解过程中将各节点的标号形式记为[Ci,Ti,αi,βi,λi],Ci表示物流作业从起点到节点i的成本费用,Ti表示到达节点i的时间,αi表示节点i之前的节点,βi表示节点i之前的运输方式,λi表示节点i的运输方式(标号中用1代表铁路,2代表公路,3代表水路,4代表航空,5代表中转)。
根据基于备选集的Dijkstra算法原理,运输网络图中的标号分为两类,一类为固定标号(S表示固定标号的集合),另一类为临时标号(∈表示临时标号的集合)。从物流作业起点开始,计算起点到各节点备选集中各中转方式的成本费用,总费用比较后将临时标号改为固定标号,找到起点到终点运输成本最小的固定标号集,固定标号集对应的节点集即为所求最短路径。其中总费用费用为ci,ci=cαi+c(βi,αi),c(βi,αi)为货物从αi出发采用βi种交通方式的成本费用(若转运则包括转运成本)。
基于备选集的Dijkstra算法的求解步骤如图1。

图1 基于备选集的Dijkstra算法求解步骤Fig.1 The Dijkstra algorithm based on an alternative set
1)根据物流作业画出运输网络图,写出各节点间实际的运输方式,在各节点进行运输方式拆分并根据经验和实际情况去掉其中不能中转路线和不存在的运输方式,得到备选集运输网络图。
2)从物流作业起点开始,记i=0,固定标号集S(0)={v0},v0为物流作业的起点。其它节点全部为临时标号记入∈,且有c0= 0,cvi=+∞,起点的标号为[0,Ti,-,-,-],其它点的标号为[+∞,-,-,-,-]。
3)比较总费用修改与固定标号相连的临时标号点。从物流作业起点出发,计算到各节点的总费用,运输时间,并按前面提到的方式标号。
4)如果运输网络中的终点得到固定标号,则计算停止。计算从作业起点到各临时标号点的总费用Ci,在各节点比较得出总费用最小的点标记为固定标号点,并将该点记入固定标号集合S中,其他点记入临时标号集合∈。若在运输网络图的终点没有得到固定标号点集合则返回3)继续计算,直到得出固定标号点集合即所求的最短路径。
3 算法举例
3.1 模型实用性验证
为验证文中模型与算法的实用性,现假设有一物流作业需将货物重量q= 100 t,单价P=1 000 元/t的货物从起点O运至终点D,运输过程中运用铁路、公路、航空、水运等4种运输方式,且经过B,C,E,F共4个节点。额定时间范围内的机会成本和惩罚成本PE=PL=100 元/h。额定货损率w=3%,货损比率ηr=0.1%,ηf=0.15%,ηs=0.08%,ηa=0.05%,ηt=1%,货损惩罚成本cw=100 元/t。算例中的相关参数如表1和表2。

表1 不同运输方式不同运输路段的相关参数
(续表1)

运输节点铁路公路水运航空时间区间C-B—12/8/12———C-E20/10/1012/10/8——[35,37]C-F15/10/12——20/7/2—F-D16/15/2010/15/18——[45,50]E-D—12/13/10—25/5/1—
注:“·/·/·”第1个数值表示运输单位货物单位运距成本,元/(t·100 km),第2个数值表示运输距离,100 km,第3个数值表示运输时间,h;时间区间表示货物运输到达节点的时间上限和时间下限,且服从一定的递增规律。

表2 各运输方式间转运成本和运输时间
注:“/”左边为运输成本,元;“/”右边为运输时间,h。
物流作业的运输网络如图2。

图2 O-D具体运输网络Fig.2 Specific transportation network diagram of O-D
实际问题中各节点间运输方式存在限制,如图2中起点O到节点A只有公路和铁路两种运输方式,节点A到B只能通过公路和航空。按照基于备选集的Dijkstra算法原理对初始运输网络图的各节点进行拆分,拆分后形成各节点备选集运输网络示意图如图3。
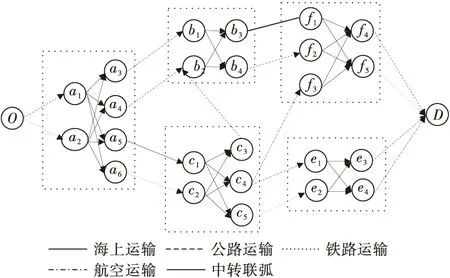
图3 各节点备选集运输网络示意Fig.3 Transportation network diagram based on alternative set of each node
结合物流作业中货物的特点和实际操作经验,某两种运输方式之间不能直接中转或实际节点不存在的中转方式,该算例中设定备选的可中转方式为:公路—铁路,公路—水运,公路—航空。去掉运输网络中各节点不能中转的路线得到的运输网络如图4。
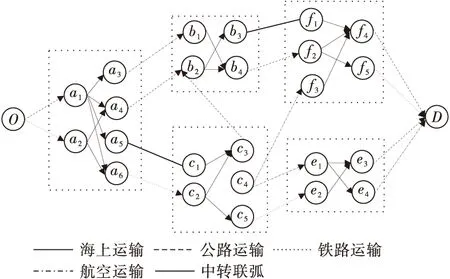
图4 去掉不能中转路线的备选集网络Fig.4 Network based on alternative set of each node remove the can not transit one
图4与图3相比各节点的可中转方式明显减少,运输网络简单化,更容易得到较优的最短路径。
暂不考虑货损率影响总费用的条件下,对运输网络中的各节点进行标号。标号完毕后,从作业终点D开始,在标号的节点中,寻找成本最小的点放入固定标号集合S中,得到一条最优路线。算例在图4的基础上,以总费用最小为约束,经过运算得出在不考虑货物损失率前提下成本相对较小的3条路径,最短路径示意如图5(图5中将运输费用最短的路径进行标号)。
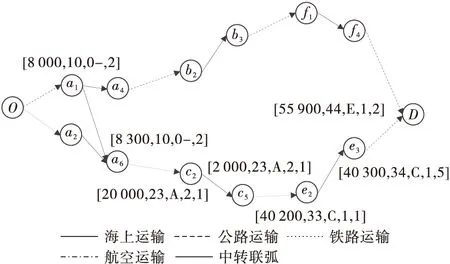
图5 最短路径示意Fig.5 Diagram of the shortest path
由图5可清晰地看出,暂不考虑货损率前提下最短路线为O—a1—a6—c2—c5—e2—e3—D。原始路径为O—A—C—E—D,运输成本为55 900 元,运输时间为44 h,运输方式为公路—铁路—铁路—铁路—公路。模型中不仅要考虑多式联运过程中运输费用及运输时间对路径选择的影响,还要考虑运输质量即货损率对路径选择的影响,下面将计算3条最短路径的货损赔付及惩罚情况,计算总的运输费用,分析是否对路径的选择有所影响。3条费用最低的最短路径,如表3。

表3 3条最短路径
(续表3)

序号运费/元路径原始路径各节点运输方式357600O—a2—a6—c2—c5—e2—e3—DO—A—C—E—D铁路—铁路—铁路—铁路—公路
运用模型中货损率及货损赔付公式计算每条路径的货损率,货损赔付及罚金,总运输费用,计算费用如表4。

表4 3条路径货损率,货损赔付及总费用
表4的计算结果表明,模型中加入运输质量控制后,第2条运输路径的费用为60 095 元,与没有运输质量控制下得到的第一条路径相比,第2条路径更优。即考虑货损的情况下最短路径为O—a1—a4—b2—b3—f1—f4—D,不考虑货损情况下的最短路径为O—a1—a6—c2—c5—e2—e3—D。各阶段的运输方式是公路—公路—公路—公路—公路,总运输费用为60 095元,总运输时间为52 h。加入运输质量控制的模型分析得出,考虑货损率对总费用的影响,最短路径选择会发生变化,更能体现路径选择过程的动态性和随机性,从而验证了模型的实用性。
3.2 模型有效性验证
模型不仅考虑随机因素对于运输成本和运输时间的影响,还考虑运输质量即货损率对总费用的影响。引入惩罚因子控制运输质量的模型对于实际运输路径优化是否有效,是验证模型有效性的关键。为验证模型的有效性,比较分析3条备选路径中货损惩罚因子为100,2 100,4 100 元/t时的总费用,计算结果如表5。
表5 惩罚因子不同的情况下最优运输路径的选择
Table 5 Selection of optimal transport path with different penalty factor

表5表明,不考虑运输质量控制时,最优运输路径为路径1,当货损惩罚因子为1 100时,总费用发生变化,此时总费用最低的路径为路径2。随着惩罚因子的不断增大,赔付费用与处以的罚金增大,最优运输路线的选择也随之发生明显变化。在物流作业终点,随着货损惩罚因子增大,承运人选择最优路径时会在考虑总费用的同时选择相对安全的运输方式来减少罚金和赔付,从而选择一条总费用少,时间短,相对较优的路径。因此,运输质量控制对最优运输路径的选择影响较大,模型在实际操作中实用性较高。
4 结 语
多式联运的运输过程易受天气、交通等随机因素的影响,这些因素会造成运输时间,运输成本和运输质量动态随机变化而使多式联运的动态路径优化复杂化。笔者针对随机因素影响的运输费用,运输时间和运输质量3个方面,建立基于软时间窗约束和引入惩罚因子运输质量控制的多式联运动态路径优化模型,以运输费用最小为目标,分析运输网络中各节点的运输路径备选集和中转情况,运用改进的Dijkstra算法找出网络中总费用最小,运输质量较好的相对较优的路径。算例表明,多式联运过程中各节点在软时间窗约束环境下运输方式的选择对运输总费用和运输质量有较大影响。运输过程中若增大对货物损失的惩罚因子,加大运输质量控制力度对多式联运的动态路径优化有较大的积极作用,对企业有较大的实用性。
多式联运是个复杂的物流系统,应该充分考虑其动态性,因此,采用更加优化的算法体现多式联运的动态性,以及从供应链角度出发加强多式联运路径优化系统同其他子系统的关联性将是今后的研究方向。
[1] Reddy V R,Kasilingam R G.Intermodal Transportation Considering Transfer Costs[C].Aruba:Proceedings of the 1995 Global Trends Conference of the Academy of Business Administration,1995.
[2] Ziliaskopoulos A,Wardell W.An intermodal optimum path algorithm for multimodal networks with dynamic arc travel times and switching delays[J].European Journal of Operational Research,2000,125(3):486-502.
[3] Boardman B S,Malstrom E M,Butler D P.Computer assisted routing of intermodal shipments[J].Computers & Industrial Engineering,1997,33(1/2):311-314.
[4] Chang Tsung-sheng.Best routes selection in international intermodal networks[J].Computers & Operations Research,2008,35(9):2877-2891.
[5] 魏航,李军,蒲云.时变网络下多式联运的最短路径问题研究[J].系统工程学报,2007,22(2):205-209. Wei Hang,Li Jun,Pu Yun.Study on the multi-modal shortest path in time-varying network [J].Journal of Systems Engineering,2007,22(2):205-209.
[6] 魏航,李军,刘凝子.一种求解时变网络下多式联运最短路的算法[J].中国管理科学,2006,14(4):56-63. Wei Hang,Li Jun,Liu Ningzi.An algorithm for shortest path under the multimodal transport of time-varying network[J].Chinese Journal of Management Science,2006,14(4):56-63.
[7] 肖天国,符卓.基于遗传算法的联合运输路径优化[J].中国科技论文在线,2008,3(10):1-2. Xiao Tianguo,Fu Zhuo.Optimizing route of multi-modal transportation based on genetic algorithm [J].Science Paper Online,2008,3(10):1-2.
[8] 范志强,乐美龙.面向随机环境的带软时间窗多式联运路径优化[J].工业工程与管理,2011,16(5):1-5. Fan Zhiqiang,Le Meilong.Research on multimodal transport routing problem with soft time windows under stochastic environment[J].Industrial Engineering and Management,2011,16(5):1-5.
[9] 刘杰,何世伟,宋瑞,等.基于运输方式备选集的多式联运动态路径优化[J].铁道学报,2011,33(10):1-6. Liu Jie,He Shiwei,Song Rui,et al.Study on optimization of dynamic paths of intermodal transportation network based on alternative set of transport modes[J].Journal of The China Railway Society,2011,33(10):1-6.
[10] 佟璐,聂磊,付慧伶.多式联运路径优化模型与方法研究[J].物流技术,2010,29(3):57-60. Tong Lu,Nie Lei,Fu Huiling.Research on optimization model and method of multi-modal transportation routing[J].Logistics Technology,2010,29(3):57-60.
Dynamic Paths Optimization of Multimodal Transport with Stochastic Factors
Chen Dandan, Hong Wei, Jia Yu
(School of Management, Chongqing Jiaotong University, Chongqing 400074, China)
Considering the dynamic and stochastic of multimodal transport and basing on transportation quality control with penalty factor, a model with the soft time windows restriction was presented for multimodal transport routing problem aiming at the minimize of total cost. Then the improved Dijkstra algorithm was used to solve the model. At last a multimodal transport problem formula based on four kinds of transport modes(the railway, highway, aviation, water transport) was designed to verify the practicality and effectiveness of the model.
traffic transportation engineering; multimodal transport; stochastic factors; optimization of dynamic paths; improved Dijkstra algorithm
10.3969/j.issn.1674-0696.2015.02.24
2012-11-05;
2013-10-09
陈丹丹(1989—),女,四川资阳人,硕士研究生,主要从事物流与供应链管理方面的研究。E-mail:279178257@qq.com。
F 252.1
A
1674-0696(2015)02-112-06

