高速列车架悬式驱动装置振动特性分析

潘嵩岩，苏 建，宫海彬，王兴宇，卢海隔，张益瑞

(1. 吉林大学 交通学院，吉林 长春 130022；2. 上海汽车集团股份有限公司技术中心，上海 201804； 3. 长春轨道客车股份有限公司，吉林 长春 130062)



高速列车架悬式驱动装置振动特性分析

潘嵩岩1，苏 建1，宫海彬2，王兴宇3，卢海隔1，张益瑞1

(1. 吉林大学 交通学院，吉林 长春 130022；2. 上海汽车集团股份有限公司技术中心，上海 201804； 3. 长春轨道客车股份有限公司，吉林 长春 130062)

为掌握高速列车架悬式驱动装置振动特性，基于Adams/Rail建立了高速列车动车仿真模型，根据修改后的德国高速轨道谱生成了仿真模型轨道不平顺空间域波形作为轨道不平顺输入激励，据此进行不同车速下直线、曲线运行时的动力学仿真，仿真结果表明：高速列车架悬式驱动装置振动响应为非平稳随机信号，轨道状况以及车辆行驶速度对其影响很大。同时齿轮箱及牵引电机的振动主要体现在横摆、沉浮、侧滚及点头运动，当通过弯道时，两部件沉浮及侧滚振动位移存在较大均值，同时齿轮箱相对构架存在较大的摇头转角均值，且各向振动幅值基本与直线行驶时的振动幅值基本相同。

车辆工程；架悬式驱动装置；振动响应分析；动力学仿真；轨道不平顺

高速列车驱动装置是将电能有效地转化为转向架轮对转矩，驱动车辆行驶。车辆运行时，驱动装置处于高速重载的运行工况，同时将承受来自轨面和车体的各种振动、冲击和作用力。

国内外学者对包含驱动装置的轨道车辆动力学特性进行了深入的研究，其中，H.Hoedei，等[1]对牵引电机不同悬挂方式下稳定性进行分析，并计算了相应的临界速度；罗赟，等[2]对架悬式驱动装置悬挂参数对机车横向动力学性能的影响进行了分析；姚远，等[3]对驱动装置弹性架悬对机车动力学性能影响机理进行研究；王勇，等[4]以半体悬式和弹性架悬式200 km/h 高速动力车为研究对象，进行2种方案的动力学性能对比分析；孙勇捷[5]建立CRH3型动车仿真模型，对不同电机悬挂参数下车辆的动力学性能进行分析。然而，目前进行动力学分析时，主要对驱动装置弹性悬挂对整车平稳性、稳定性及曲线通过性等动力学性能指标的影响进行分析，而未对驱动装置的振动特性进行研究。

车辆运行时驱动装置各部件的剧烈振动的分析及复现是进行可靠性试验时动力学模拟的重要内容之一[6]。为掌握架悬式驱动装置的全轴振动环境，笔者首先对其结构进行分析，利用Adams/Rail软件建立包含驱动装置的整车动力学仿真模型，进行车辆在不同车速下直线、曲线运行时的动力学仿真，分析牵引电机和齿轮箱振动响应，研究两者振动特性随车速、运用线路条件变化的规律。

1 架悬式驱动装置的结构特点

高速列车驱动装置包括牵引电机、齿轮箱、联轴器等，根据牵引电机悬挂方式可分为轴悬式、架悬式和体悬式，为了满足列车高速运行时的动力学性能,高速列车牵引传动系统多采用体悬或架悬的结构方式，其中我国自主生产的CRH1，CRH2，CRH3型动车组均采用驱动装置架悬式。

典型的驱动装置架悬式动力转向架结构如图1，每台动力转向架包括两套驱动装置，将牵引电机直接或通过固装在转向架构架上。齿轮箱一端通过两个轴承支撑在车轴上，另一端通过悬吊装置与转向架构架相连。从动大齿轮直接压装在车轴上，牵引电机与齿轮箱采用能适应各向相对运动的齿轮联轴器联结传递扭矩。

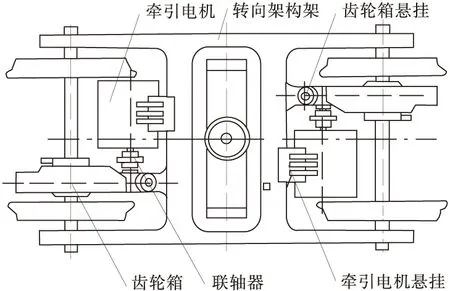
图1 典型驱动装置架悬式动力转向架结构Fig.1 Typical structure of bogie with driving device flexible suspension

2 动力学仿真模型的建立

2.1 基于Adams/rail的整车模型

Adams/Rail是专门用于研究铁路机车、车辆、列车和线路相互作用的动力学分析的专业应用软件包，是世界上主流铁道车辆系统动力学仿真软件之一。以CRH3高速列车为研究对象，基于Adams/Rail建立转向架及整车模型，分别如图2、图3。

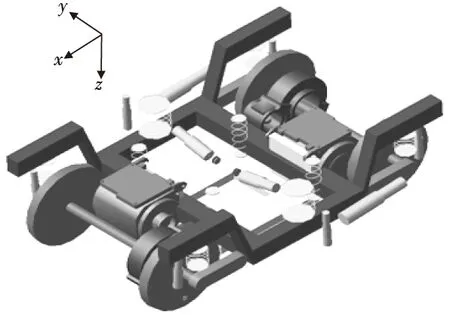
图2 动力转向架模型Fig.2 Model of power bogie

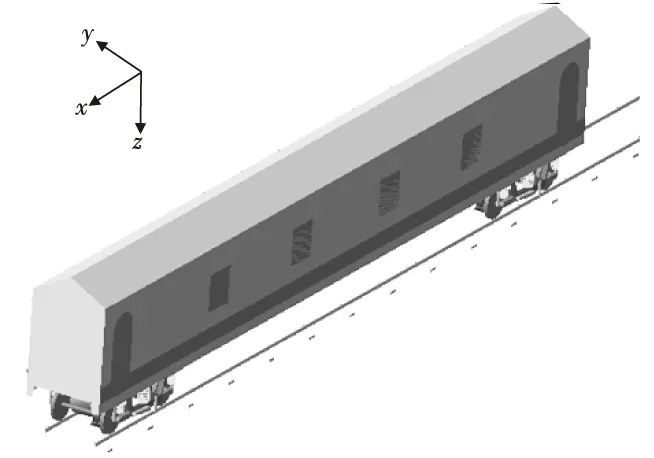
图3 整车仿真模型Fig.3 Simulation model of motor car

定义牵引电机及齿轮箱所具有的6个自由度运动分别为：沿x，y，z轴的伸缩、横摆及沉浮运动；以及绕x，y，z轴的侧滚、点头及摇头运动。

2.2 轨道不平顺空间域模型

国外内对轨道谱进行了大量的研究，分别提出了不同的轨道不平顺功率谱密度表达式，如美国轨道谱、德国高速轨道谱及秦沈客运专线轨道谱等，对准高速的机车车辆可采用美国6级谱，但对高速机车车辆应采用德国高速谱。我国在研究高速机车车辆的动态响应时, 也规定采用修改后的德国高速轨道谱[7-8]，其表达式为：

高低不平顺：

(1)

方向不平顺：

(2)

水平不平顺：

(3)

式中：Ω为轨道不平顺的空间频率，rad/m；Ωs，Ωc，Ωr分别是截断频率，rad/m；Sv(Ω)，Sa(Ω)分别为高低、方向不平顺功率谱密度，m2·(m/rad)；Sc(Ω)为水平不平顺功率谱密度，由于采用倾角度量，(rad/m)-1；Av，Aa分别为粗糙度常数，m2·(rad/m)；b为左右滚动圆距离的一半，一般取0.75 m。

通过对功率谱密度函数直接离散采样，构造出频谱，然后进行傅里叶逆变换，即可得到轨道不平顺空间域模型，其具体过程及生成的轨道不平顺空间域波形限于篇幅不再此赘述。至此建立了完整的整车动力学仿真模型。

3 驱动装置振动响应仿真与分析

为研究车辆运行时轨道随机不平顺作用下的牵引电机及齿轮箱振动特性，分别在不同速度下直线行驶及300 km/h时R9000曲线行驶的运行状态下进行整车动力学仿真。

3.1 直线行驶时振动响应分析

分别进行以200，300 km/h速度直线行驶运行状态下整车动力学仿真，对牵引电机振动特性进行分析，如图4。

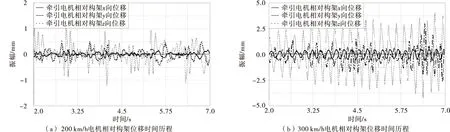
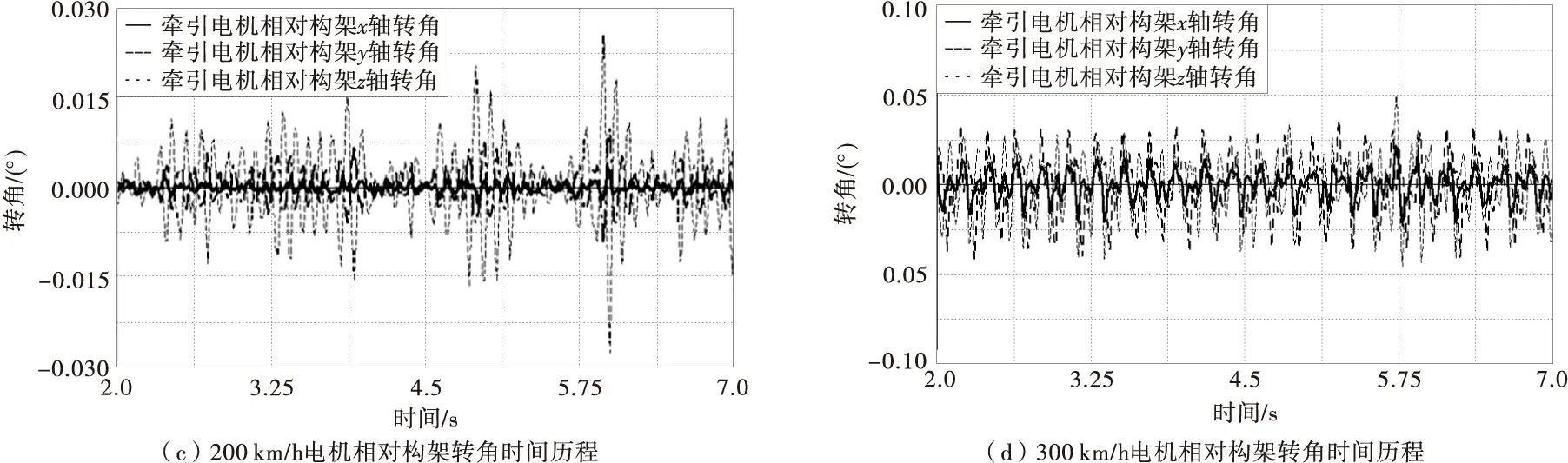
图4 直线行驶时电机振动响应历程Fig.4 Vibration response process of motor when drive straight

对200，300 km/h运行速度下直行时牵引电机振动响应历程分析可知，与200 km/h运行速度相比， 300 km/h运行速度下牵引电机相对构架的三向位移、转角均显著增大，由于电机吊架横向刚度较小，垂向及纵向刚度较大，牵引电机相对构架横向位移幅值最大，最大值为4 mm，垂向、纵向位移幅值均较小。其中，300 km/h运行速度下纵向相对位移幅值为0.25 mm，垂向位移峰值为3 mm。牵引电机相对转向架构架的三向转动角度均较小，最大转角幅值均小于0.05°。

同样地，对齿轮箱的振动响应进行分析，如表1。可知300 km/h运行速度下齿轮箱振动响应幅值比200 km/h速度运行时亦显著增大。齿轮箱相对构架的转角主要体现在侧滚运动和点头运动。其中，点头运动的幅值最大，摇头运动幅值约为0°；齿轮箱质心相对构架的三向位移中，主要表现为沿z轴的沉浮运动和沿y轴方向的横摆运动；其中，垂向位移振幅最大，而沿x轴方向的伸缩运动振幅最小。

表1 直线行驶时齿轮箱相对构架振动响应

3.2 曲线行驶时振动响应分析

为研究车辆曲线行驶时驱动装置中牵引电机及齿轮箱振动状态，进行300 km/h速度下车辆R9000弯道曲线运行仿真分析，如图5。

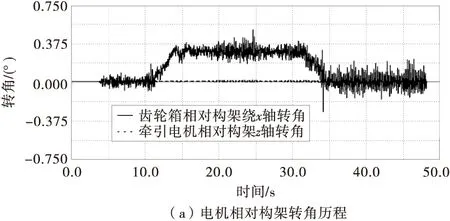
图5 曲线通过时电机振动响应历程Fig.5 Vibration response process of motor when went around the curve

牵引电机及齿轮箱相对运动时，由于牵引电机、齿轮箱绕y轴方向的点头运动产生的两者相对运动表现为两者垂向位移，故分析时仅分析两部件的绕x轴、z轴的转角。当车辆通过弯道时，牵引电机相对构架绕x轴侧滚运动转角产生为0.3°的均值，而绕z轴的摇头运动转角基本可以忽略，相应的，牵引电机相对构架的三向平移运动中，存在均值为29.4 mm的沉浮位移均值，而横摆、伸缩运动均值为0，横摆运动幅值为4.5 mm，伸缩运动幅值约为0，三向平动及侧滚转角幅值与车辆直线行驶时振动位移幅值基本相同。

进一步对300 km/h运行速度下曲线行驶时齿轮箱的振动响应进行分析，如表2。齿轮箱相对构架侧滚、摇头运动转角均存在较大均值，分别为0.3°，0.25°，幅值分别为0.15°，0.26°；相应的，齿轮箱相对构架的三向平移运动中，存在均值为40 mm的沉浮位移均值，横摆、伸缩运动均值为0，横摆运动幅值为4.5 mm，伸缩运动幅值为0.3，三向平动及侧滚、摇头转角幅值亦与车辆直线行驶时振动位移幅值基本相同。

表2 通过曲线时齿轮箱相对构架振动响应

3 结 论

针对高速列车架悬式驱动装置振动特性，建立了整车仿真模型，并进行不同车速下直线、曲线运行时动力学仿真，并对牵引电机和齿轮箱的振动响应分析，该分析结果为进一步运行仿真分析及室内驱动装置可靠性试验台架振动环境模拟提供了参考，并得到如下结论：

1)齿轮箱及牵引电机振动响应为非平稳随机信号，轨道状况以及车辆行驶速度对传动系统振动响应影响很大，随着车速的提高，车辆各部件振动加剧，振动位移幅值及频率都显著增大。

2)车辆直线行驶时，牵引电机相对构架的横向位移振幅较大，纵向位移及三向转角振幅很小;齿轮箱相对转向架构架的沉浮、横摆位移以及侧滚、点头转角振幅较大，而纵向相对位移及摇头运动转角振幅很小。

3)当车辆通过弯道时，齿轮箱、牵引电机侧滚、沉浮运动均产生较大转角或位移均值，同时齿轮箱相对构架存在较大的摇头转角均值，各向振动幅值基本与直线行驶时的振动幅值基本相同。

[1] Hoedei H,Haigermoser A.高速机车现代化转向架设计的发展[J] .电力牵引快报,1995(8):69-77. Hoedei H,Haigermoser A.Entwicklung Eines Modernen T riebdrehgestellkonzer Fuer Hochleistung slo komotive[J] .Electric Traction Journal,1995 (8):69-77.

[2] 罗赟,金鼎昌.架悬机车驱动装置悬挂参数规律的研究[J].中国铁路科学,2007,28(4):78-82. Luo Yun,Jin Dingchang.Research on the rules of suspension parameters to driving equipments suspended in bogie frames[J].China Railway Science,2007,28(4):78-82.

[3] 姚远,张开林,张红军,等.机车驱动系统弹性架悬的机理与应用研究[J].铁道学报,2013,35(4):23-29. Yao Yuan,Zhang Kailin,Zhang Hongjun,et al.Mechanism of drive system elastic suspension and its application[J].Journal of the China Railway Society,2013,35(4):23-29.

[4] 王勇,陈康.半体悬式与弹性架悬式200 km/h高速动力车动力学性能对比分析[J].机车电传动,2012(2):7-9. Wang Yong,Cheng Kang.Contrast and analysis of dynamic performance of 200 km/h high-speed power cars with semi-body and flexible suspensions [J],Electric Drive for Locomotives,2012(2):7-9.

[5] 孙勇捷.高速动车弹性架悬式驱动装置动力学性能研究[D].成都:西南交通大学,2011. Sun Yongjie.Research on Dynamic Performance of the Driving Device Flexibly Suspended on Frame about High-Speed Motor Car[D].Chengdu:Southwest Jiaotong University,2011.

[6] 牛贝妮.高速动车组传动系统可靠性振动试验台模型设计与分析[D].长春:吉林大学,2012. Niu Beini.Design and Analysis the Model of Reliability Testing Equipment of High-Speed Train Transmission System[D].Changchun:Jilin University,2012.

[7] 王福天,周劲松,任利惠.用于高速车辆动态仿真的轨道谱分析[J].铁道学报,2002,24(5):21-27. Wang Futian,Zhou Jinsong,Ren Lihui.Analysis on track spectrum density for dynamic simulations of high speed vehicles[J].Journal of the China Railway Society,2002,24(5):21-27.

[8] 魏冲锋.轨道不平顺功率谱时域转换及其应用研究[D].成都:西南交通大学,2011. Wei Chongfeng.Time Domain Conversion and the Application Research of Track Irregularity Power Spectrum[D].Chengdu:Southwest Jiaotong University,2011.

Vibration Characteristic Analysis of Frame-MountedDriving Device for High-Speed Train

Pan Songyan1, Su Jian1, Gong Haibin2, Wang Xingyu3, Lu Haige1, Zhang Yirui1

(1. Transportation & Traffic College, Jilin University, Changchun 130022, Jilin, China; 2. SAIC Motor Technical Center, Shanghai 201804, China; 3. Changchun Railway Vehicles Co. Ltd., Changchun 130062, Jilin, China)

In order to master vibration characteristic of high-speed train’s frame-mounted driving device, a simulation model of high-speed train’s motor car was established based on Adams/Rail, and track irregularity spatial-domain waveform was generated according to the modified German high-speed rail spectrum. At last, the dynamics simulations were carried out under different speeds. Simulation results show that the vibration response of driving device is a non-stationary random signal, and is affected by track conditions and speed. And the vibrations of gearbox and motor were mainly presented as yaw, ups and downs, roll and nodding motions. The ups and downs displacements and roll rotation angle of these two components show high mean values as the vehicle went around the curve, while vibration amplitudes are basically the same compared with straight driving.

vehicle engineering; frame-mounted driving device; vibration response analysis; dynamics simulation; track irregularity

10.3969/j.issn.1674-0696.2015.02.33

2013-06-13；

2013-10-18

吉林省科技发展计划资助项目( 20080356)；长春市科技支撑计划项目(2010018)

潘嵩岩(1983—)，男，吉林长春人，工程师，硕士研究生，主要从事车辆检测与诊断方面的研究。E-mail:pansy@jlu.edu.cn。

U 260.11

A

1674-0696(2015)02-152-04