基于高职院校课程改革系统应用设计的研究

张竞予，王 伟

（1.陕西铁路工程职业技术学院 陕西 渭南 714000；2.中铁一局集团有限公司 陕西 西安 710054）

目前随着高职院校改革的推进，其办学规模和学生数量日益扩大增多，高校课程设置安排这一基本工作的重要性凸显，其实质是根据教学计划中所设置的课程安排合理的时间和地点，特别在教师、教室和时间等教学资源有限的条件下，对课程进行有效的优化组合，保证教学工作顺利进行，涉及因素多，是一项复杂多元化的系统问题工程。高校排课问题已被证明是一个NP完全问题，由于其具有多元复杂难解性，一直未得到很好的合理性解决[1]。

排课在各项高校教务工作中的地位处于重中之重，主要体现在课程编排的合理性不仅自接关系到每个学生的学习效率高低，而且教师教学效果的好坏以及教室等教学资源充分合理的利用率等都与其息息相关。此外排课又是所有教务工作中最繁杂的，不仅要考虑教师、学生、教室在排课时间约束下的要求，还要考虑各排课约束元因子之间的合理性，具体表现在课程存在着如分阶段、分合班、单双周、前后节、教师多课头、大小教室、特殊教室等诸多复杂要素的影响，使得排课工作的繁复性激增，所以借助计算机自动排课是必须的。许多学者就排课问题进行了广泛的研究，并且提出了多种解决问题的算法。传统的排课算法主要有专家系统法、图论和贪婪算法等等[2]，而这些方法仅仅针对个别实际问题并不具备通用性，同时由于其关联规则较难获取而导致求解的结果并不十分理想。由于随着近几年智能技术的飞速发展，模拟退火算法、遗传算法等效果较好的启发式算法成为当前排课问题的主要解决方法。为了进一步降低冲突，提高排课效率和成功率，提出一种基于自衍生遗传算法的排课系统，在传统遗传算法的基础上进行编码方式的改善，针对其交互、演变性算法进行自衍生操作从而加快其收敛速度，将其应用于高校排课问题求解，实验结果表明，自衍生遗传算法提高了高校排课效率和成功率，降低排课冲突率，满足了排课问题的约束元条件，很好的解决了排课问题。

1 排课系统问题分析

1.1 排课系统需求目标

教学任务的安排是一个充满矛盾冲突的过程，主要矛盾冲突表现在任课教师、开设课程、授课时间、班级和地点等多方面需求对某一教学资源的需求，产生矛盾冲突，进而导致教学工作不能正常合理的进行。概括来讲排课的目标就是根据教学进度任务计划，来将教师、教室、课程和班级合理地安排在一周内某一个不产生矛盾冲突的时间段中，并能保证排课系统正常工作，所以排课问题实质上是一个在多约束元制约条件下的资源合理分配的问题。

1.2 排课系统的约束元

1）刚性约束元。在具体排课工作中必须要遵寻满足的约束机制包括：在同一时间段内同一教师只能够安排一门课程；在同一时间段内同一学生只能够安排一门课程；在同一时间段内同一教室只能够安排一门课程；被安排的教室座位数应大于该门课程上课时总人数。此外个别班级人数差别较大，且存在着许多班级组合与拆分的情况，例如具有实验环节的课程的实验部分为分班课，而基础类课程则为多班合上的大课，一些专业基础课为两三个专业合上的小合班课等。所以高校排课系统除了要考虑按基本班排课外，还要考虑合班上课与分班上课情况的情形，另外还包括按班级公共选修课排课的情形。高校一般没有班级的固定教室，并且教室具有多样性，如阶梯教室、大小教室，多媒体教室、机房和专业实验实训室等。教师存在着一个教师上多门课和多个教师合上一门课的情况。某些课程的周学时存在着单数的情况，前后节组合的问题解决，某些专业还存在一段时间连续上课的情况。

2）柔性约束元。如上所述可以看出排课中不仅排课刚性约束元的繁杂性强，最主要的对排课原则性要求是必须遵循的，即刚性约束元不能冲突这一排课必要条件。此外排课时还应考虑刚性约束元内部和相关联性的一些非必要性的原则，即合理性柔性约束元。具体表现为：班级的课程在一周时间安排上要尽量分布均匀；同一教师的课程，在总体分布均匀合理且日课程量不超过四节的前提下，尽量安排在同一天以利于保证教师的授课效果，同时减少教师多次和返学校所耗费的时间；保证同课程时间间隔的均匀性，避免一门课程连续上两天或三天的情况；由于高校班级上课地点不固定，如果一个班的课程大多数被安排在相对固定的教室，不但可以减少学生课间换教室所耗费的时间，还能增强学生的班级归宿感；鉴于班级人数小等和教室容量小一的实际情况，还应避免小班课程占用大教室的情况，优先保证多班的合班课程对大教室的需求，以充分有效得利用教室资源[3]；体育类高强度活动课程应避免安排在理论类讲授课程之后，所以其应安排在下午或上午3、4节。

2 排课系统设计

2.1 排课系统工作流程

排课工作每学期末首先由教务处根据各院系制定的学期教学任务进度计划，根据上课的刚柔件约束元条件生成下一学期的教学任务，然后下发给系部教研室各教学单位，再根据教学单位返回的具体教学任务，制定全校各班级的课表及教师课程任务单。

2.2 刚柔性约束元数据库设计

1）模型结构设计

图1 排课系统模型图Fig.1 Course scheduling system model diagram

2）逻辑关系设计。根据上述模型结构设计所得到的系统模型，该排课系统主要涉及到的数据库主要包括班级信息、教师信息、教室信息、时间信息、课程信息以及教学任务进度计划信息。

2.3 遗传算法设计

根据系统的具体情况文中采用的遗传算法设计，对传统算法的做了适当的改进，具体设计步骤如下。

1）排课问题编码:由于传统遗传算法是采用二进制来进行编码的，结合高校排课问题的特殊性再采用传统二进制编码方式已使排课信息难以正确表达。因此本文采用一种改进的编码方式——自然编码，如图2所示，其中L表示课程，T表示时间，C表示教室。

2）初始族群的生成:因为传统遗传算法采用的是随机方式来产生初始族群，所以较容易的得到局部最优排课方案，产生早熟现象，为此本文根据课程多少来动态安排族群的大小，采用均布设计方案来产生初始族群，使排课方案的初始解尽可能均匀分布在解的空间中，这样不仅保证了遗传算法得到全局最优排课方案，而且在加快寻优时间提高收敛速度和排课效率的同时，很好避兔了局部最优排课方案过早出现。

图2 遗传算法单体表示Fig.2 Genetic algorithm monomer said

3）适应度值计算:按照适应度函数计算适应度值，排课问题的实质就是在满足多种约束元的情况下得到最佳教学资源分配利用效果的排课方案。由于在遗传算法的进化过程中，其是由适应度函数来确定进化的发展方向的，所以适应度函数就直接决定了排课方案的寻优速度和找出最优排课方案的成功率。由于排课问题具有多个目标的特性，其适应函数应该满足各个目标从而达到最优化。

式中α、β和γ分别为系统各目标的权重值。

4）选择操作：系统排课时选择操作采用如图3所示的轮盘赌选择法[4]，即将轮盘根据各单体适应度值的大小进行区域分配，按其不同比例划分区域，单体的适应度数值越高，则其相应所占的比例就越大，其存活的概率就更大，进而进入下一代族群的机率也就越大。

图3 单体轮盘赌选择方法Fig.3 Monomer roulette wheel selection method

5）自衍生交叉和变异操作：首先交叉操作主要是针对两个单体通过交叉组合从而产生更加优异的单体，而变异操作则主要是对研究单体进行变异而得到新一代更加优秀的单体，所以不难看出，交叉和变异操作在遗传算法的收敛速度以及解的质量方面起着核心控制作用，而由于传统的遗传算法交叉和变异操作在概率的方面采用固定方式，导致使单体在进化后阶段的丰富多样率大大降低，从而使局部最优解过早出现[5]。针对这一问题为了提高排课问题求解的效率，消除局部最优解的现象的发生，本文主要针对对传统遗传算法中交叉和变异方式进行了改良，提出采用适应的交叉和变异操作，以下为其具体操作运行方式。

式中Pi、Pj——分别为交叉和变异概率；g——变异单体的适应度值；g′——交叉中适应度值较大的单体；k1、k2——分别为（0，1）的随机性。

通过以上操作方式的改进，不但增强种群中单体的丰富多样性，而且很好的避免了局部最优解过早出现的现象。

6）冲突检测消除:经过交叉和变异操作后可能仍会会产生冲突，所以还需要进行冲突再检测并解决冲突已获得最优解[6]。

2.4 自衍生遗传算法系统求解流程

根据遗传算法各种操作改良后的自动排课系统工作过程主要为:首先进行排课问题解的初始化过程，也就是产生遗传算法初始族群；接着以自然编码方式对排课问题进行编码操作；计算出每一排课方案的适应度值；运用轮盘赌方式选择出更为优良好的单体产生排课方案下一代族群；接着对族群中的单体通过交叉和变异操作产生新的单体，计算其适应度值对判断其是否进入下一代[7]；判定全局最优排课方案是否满足要求，如果找到则进化结束并输出，如果不满足再回转至第三步系统操作过程。系统操作主要流程如图4所示。

3 计算机排课系统实现与结果

3.1 排课系统实现

图4 排课系统工作流程图Fig.4 Course scheduling system work flow chart

为了进一步检验本文算法的可靠性通过将其与模拟退火算法和传统的遗传算法进行了对比试验，通过运用VC++编程方法来进行实现[8]。排课系统各约束元素分布如表1所示，系统遗传算法的控制要素设置情况如表2所示。

表1 排课系统约束元素表Tab.1 Course scheduling system constraint element table

表2 系统控制要素设置表Tab.2 System control factors set the table

3.2 结果分析

从表3所示3种方法的运行结果不难看出，本文改进的遗传算法比模拟退火算法和传统遗传算法效果好，对比结果表明不仅在最优排课方案所需时间要少，而且在矛盾冲突率和成功率方面优于其他方法，解决排课问题总体效果好。总之通过采用本文算法进行排课不仅提高了排课效率，排课的成功率达到100%，而且在提高教室利用率充分运用教学资源方面也有很好的效果，说明了本文算法是一种成功率高、综合性好的排课方法。

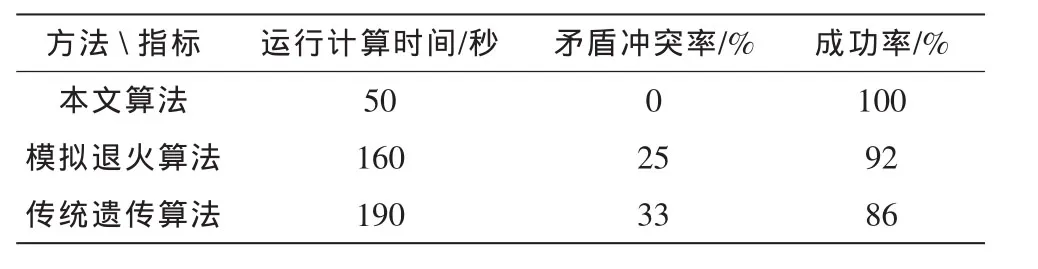
表3 系统运行结果对比表Tab.3 The contrast table of systematic operation result

4 结束语

计算机技术为现代化教育带来了方便、快捷，通过采用计算机排课系统，不但大大节省人力、物力，而且也减少了课程冲突。本文针对排课特点，结合遗传算法的优点，对遗传算法又进行了一些改良，结果表明，自衍生遗传算法在一定程度上能够解决高校排课难题。通过本文系统算法较大程度上减少教务人员的工作量，而且进一步优化解决了传统排课算法效率低，课程冲突率高，影响教学效率等问题，具有一定的借鉴使用价值。

[1]张长庚.基于遗传算法的浙江水利水电专科学校排课系统设计与实现[D].成都：成都电子科技大学，2010.

[2]Rxghu Ramakrishnxn，Johxnnes Gchrkc.数据库管理系统原理与设计[M].北京：清华大学出版社，2004.

[3]胡世清.高校排课多元优化策略与自动实现方法的研究[J].现代教育技术，2011（7）:105-109.HU Shi-qing.Research of university course arrangement multivariate optimization strategy and automatic realization method[J].Modern Educational Technology，2011（7）:105-109.

[4]张小红.高校排课系统的设计与实现[J].电子科技，2012（7）:45-47.ZHANG Xiao-hong.Design and realization of college course scheduling system[J].Electronic Science and Technology，2012（7）:45-47.

[5]张立岩，张世民，秦敏.基于改进粒子群算法排课问题研究[J].河北科技大学学报，2011，3 （2）:265-268.ZHANG Li-yan，ZHANG Shi-min，QIN Min.Research in improved particle swarm optimization for schedule arrangement[J].Journal of Hebei University of Science and Technology，2011，3（2）:265-268.

[6]闰保权.改进的遗传算法在排课系统中的应用研究[J].信息技术，2011（9）:125-127.YAN Bao-quan.Application of improved genetic algorithm incourse scheduling system[J].Information Technology，2011（9 ）:125-127.

[7]李梅云.基于遗传算法的排课编码设计[J].漳州职业技术学院学报，2011（3）:22-27.LI Mei-yun.The course code design based on genetic algorithms[J].Journal of Zhang zhou Institute of Technology，2011（3）:22-27.

[8]董冬，张少博，刘晓.试验状态信息管理软件设计[J].火箭推进 ，2013（6）:72-77.DONG Dong，ZHANG Shao-bo，LIU Xiao.Design of information management software for test status[J].Journal of Rocket Propulsion，2013（6）:72-77.