基于FDTD的结构耦合对超声传播影响的仿真研究

胡嘉玲，季爱明，毛凌锋

（苏州大学 智能结构与系统研究所，江苏 苏州 215000）

超声检测是无损检测技术中研究和应用最活跃的方法之一，广泛地应用于缺陷的识别和检测中。随着超声检测技术的不断发展，微小缺陷的检测成为了研究热点。通过建立非线性超声检测系统，能够实现对金属材料中微纳米级裂纹的检测[1]。而实际检测中，缺陷不仅以单个的形式存在，还会以多个或缺陷群的形式存在，因此，多缺陷的检测也成了新的研究方向。由于含有多个缺陷情况的散射比单个缺陷情况复杂，实际检测分析较困难，因此了解多缺陷信息对超声波检测起着重要的作用[2]。类似于各类孔缝与电磁脉冲的耦合效应[3]，在进行多缺陷检测时，需要考虑缺陷间的耦合效应。同时，与量子力学中的量子尺寸效应[4-5]相似，当检测件尺寸变化时，对超声检测的结果也会产生影响，需要对结果进行修正[6]。

本文基于时域有限差分法（FDTD）建立了一个和3个空腔的铝板模型，用仿真软件SimSonic[7]对模型中超声信号的传播进行仿真，研究不同铝板宽度时的声场特性，分析了考虑尺寸效应下结构的耦合对声波传播特性的影响，从而为超声检测中传感器所接收的信号进行修正奠定基础。

1 方法与建模

本文采用基于时域有限差分法的超声仿真软件SimSonic对结构进行仿真。该仿真计算基于以下弹性动力学方程

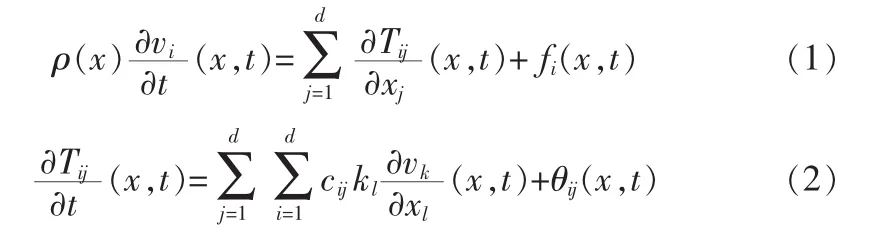
公式（1）和（2）描述了弹性波在连续介质中传播的规律。其中 x和 t分别是空间和时间变量。 ρ（x）是密度，c（x）是四阶刚度张量。这些参数可用来定义材料属性和仿真结构。

在仿真建模时，随着仿真模型的维数增加，仿真计算所占用的计算机资源将急剧增加，在对仿真结果不会造成较大影响的铝板下，有必要对仿真模型进行简化，因此考虑建立二维模型[8]。仿真模型为中间有圆形空腔的铝板，铝板的四周设置完全匹配层（PML）吸收边界[7]。铝板长度为50 mm，仿真中改变铝板的宽度。仿真中不考虑材料对超声的吸收。

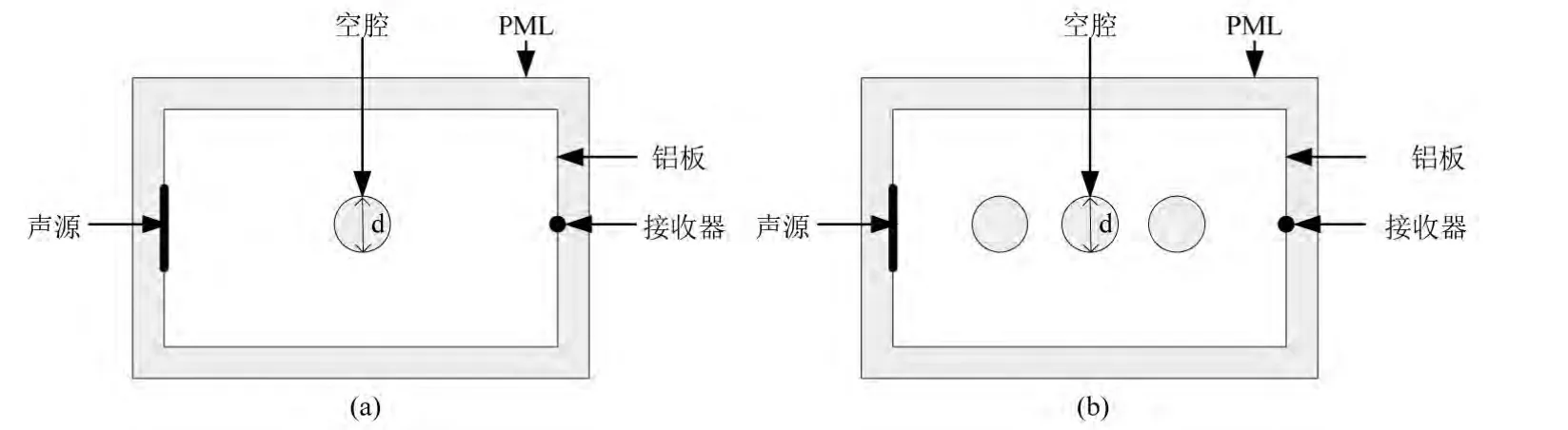
图1 仿真系统框图Fig.1 Simulation system block diagram

2 仿真结果与讨论

2.1 时域信号

铝板宽度分别取7.5 mm、15 mm和20 mm时，传感器接收的透射超声时域信号如图2所示。

从图中可以看出，在开始的一段时间里，信号幅度不稳定，处于非稳态，40 μs之后逐渐达到稳态。 观察图 2（a），即一个空腔的铝板，铝板宽度为7.5 mm时，稳态信号幅度最大。铝板宽度为15 mm时，稳态信号幅度减小。铝板宽度为20 mm时，信号幅度比7.5 mm和15 mm宽度时小很多。由此可见，铝板宽度的变化对超声透射信号有明显的影响。而三个空腔时，稳态信号幅度随铝板宽度的变化与一个空腔时相比较小，且各宽度对应的信号幅度也较小。

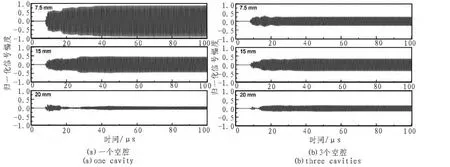
图2 不同宽度下透射超声时域信号Fig.2 Time-domain transmitted ultrasonic signal under different widths

2.2 波场快照

图3所示为80 μs时刻，不同铝板宽度下的波场快照图。

图3 不同宽度下80 μs时刻的波场快照图Fig.3 Snapshots for 80 μs under different widths

从图中波纹的颜色深浅可以看出声压强度的大小。由于铝和空腔的声阻抗不同，使得声波在遇到空腔时产生了反射和散射[9]。观察图3（a），即一个空腔的铝板，当铝板宽度为7.5 mm时，可以观察到明显的衍射波纹，空腔右侧的透射声压明显较大。同时，来自空腔和铝板边界的反射也较强烈，使空腔左侧的声压也很大。当宽度为15 mm时，空腔附近的衍射波纹减弱，透射声压明显减小。当宽度为20 mm时，衍射波纹几乎消失，透射声压进一步减小。由此可见，铝板宽度变化对超声的传播有较大的影响。3个空腔时，从图中可以看出，两个空腔的增加，使空腔之间产生耦合效应，干扰了衍射波的传输，来自空腔和铝板边界的反射波共同减弱了衍射波的传输。空腔右侧的透射声压远小于一个空腔时对应宽度下的透射声压。

2.3 稳态功率及其相对变化

设铝板宽度在6 mm～40 mm之间变化，得到稳态功率均值随宽度的变化规律，如图4中的实心圆圈实线所示。观察图4（a）和（b），当铝板宽度小于 20 mm，即 8 个波长时，透射信号的稳态功率均值与更大宽度时相比明显增大，其中出现两次峰值。对于一个空腔的铝板，两个峰值分别在宽度为7.5 mm和16 mm时出现，其中7.5mm时最大。而对于3个空腔的铝板，两个峰值分别在宽度为12 mm和17 mm时出现，其中12 mm时最大。宽度大于20 mm之后，稳态功率均值呈现周期性波动，其幅值明显小于前两个峰值。但3个空腔时，稳态功率均值随宽度的变化没有一个空腔时明显。

为了比较宽度变化时稳态功率均值的相对变化，将宽度大于20 mm的稳态功率均值求平均，设为p0。再设稳态功率均值为p，其相对变化为r，利用公式：

可求得r，如图4中的空心圆圈虚线所示。对于一个和3个空腔的铝板，稳态功率均值的相对变化均出现两次峰值，但3个空腔时的峰值与一个空腔时相比出现了偏移，且比一个空腔时的幅度要小。

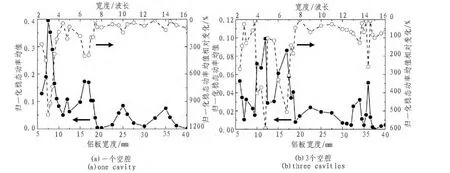
图4 不同宽度下归一化稳态功率均值及其相对变化Fig.4 Normalized mean steady－state power and its relative change as a function of width

把两种结构下的归一化稳态功率均值相对变化放在一起进行比较，如图5所示。

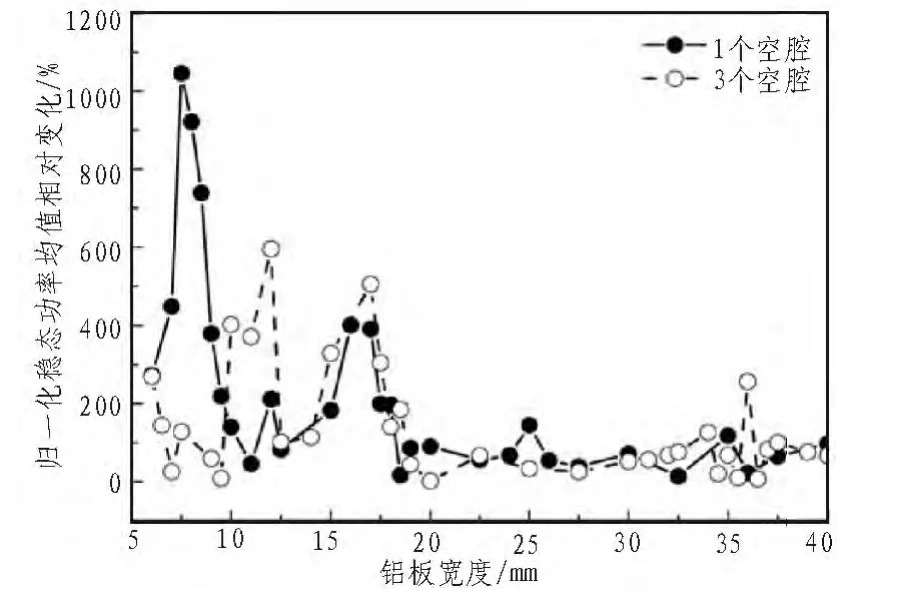
图5 不同宽度下归一化稳态功率均值相对变化Fig.5 Relative change of normalized mean steady-state power as a function of width

从图中可以看出，当宽度小于20 mm时，稳态功率均值的相对变化较大，对于一个和3个空腔的铝板，该相对变化分别在宽度为7.5 mm和12 mm时达到最大，最大相对变化率分别为10.5倍和6倍左右。3个空腔时，铝板宽度变化对稳态功率均值的影响与一个空腔时相比要小。这是因为空腔之间的耦合效应。由此可知，空腔的耦合对尺寸效应具有抑制作用。

3 结 论

本文建立了一个和3个空腔的铝板模型，用时域有限差分法仿真研究了考虑检测件尺寸变化时，结构的耦合对声场特性的影响。仿真分析的结果表明，对于一个空腔的铝板模型，当铝板宽度小于8个波长 （20 mm）时，空腔与铝板的耦合效应较明显，超声透射信号的功率明显增大，稳态功率均值的相对变化在宽度为3个波长 （7.5 mm）时最大，达到10.5倍，具有明显的尺寸效应。而对于3个空腔的铝板模型，当宽度小于20 mm时，超声透射信号的稳态功率均值的相对变化比一个空腔时要小，其最大相对变化在宽度为12 mm时达到6倍。由此可知，空腔的增加加强了空腔之间的耦合，从而削弱了空腔与铝板的耦合效应，进而减弱了尺寸效应。研究结果表面在用超声波进行无损检测时，对于小尺寸的零件，结构间的耦合效应和零件的尺寸效应会使得检测结果产生偏差，因此需要对检测的结果进行修正，以减少测量误差。研究结果为修正小尺寸复杂结构零件的超声检测中的检测结果奠定了基础。

[1]敦怡，师小红，王广龙，等.微纳米级裂纹的非线性超声检测[J].光学精密工程，2011，19（1）:132-137.DUN Yi，SHI Xiao-hong，WANG Guang-long，et al.Nonlinear ultrasonic test of micro-nano crack[J].Optics and Precision Engineering，2011，19（1）:132-137.

[2]倪云鹿.固体介质多缺陷超声波散射的有限元数值模拟[D].青岛：中国石油大学（华东），2008.

[3]孙延鹏，安小鹤，孙红鹏，等.基于FDTD的环形孔缝电磁耦合规律研究[J].电子设计工程，2014，22（9）:57-61.SUN Yan-peng，AN Xiao-he，SUN Hong-peng.Study on characteristicsofelectromagnetic coupling into annular aperture based on FDTD[J].Electronic Design Engineering，2014，22（9）:57-61.

[4]Li W H，Yang C C，Tsao F C，et al.Quantum size effects on the superconducting parametersofzero-dimensionalPb nanoparticles[J].Physical Review B，2003，68（18）:184507.

[5]Mao L F.Dot size effects of nanocrystalline germanium on charging dynamics of memory devices[J].Nanoscale Research Letters，2013，8（1）:1-4.

[6]Piquette J C.Technique for detecting the presence of finite sample size effects in transmitted wave measurements made on multilayer underwater acoustic panels[J].Journal of the Acoustical Society of America，1991，90（5）:2831-2842.

[7]Bossy E，Talmant M，Laugier P.Three-dimensional simulations of ultrasonic axial transmission velocity measurement on cortical bone models[J].Journal of the Acoustical Society of America，2004，115（5）:2314-2324.

[8]Hastings F D，Schneider J B，Broschat S L.Application of the perfectly matched layer （PML）absorbing boundary condition to elastic wave propagation [J].Journal of the Acoustical Society of America，1996，100（5）:3061-3069.

[9]董欣，孙继华，韩晓华，等.钢中非金属夹杂超声检测的计算机模拟[J].科学技术与工程，2009，9（4）:1039-1042.Dong Xin，Sun Ji-hua，HAN Xiao-hua，etal.Computer Simulation to the ultrasonic testing of nonmetallic inclusions in steel[J].Science Technology and Engineering，2009，9（4）:1039-1042.