基于相关向量机的氢气传感器故障恢复方法

王 冰，张震宇，刘 慧,张洪泉

(1.哈尔滨工程大学信息与通信工程学院，黑龙江哈尔滨 150001；2．中国电子科技集团公司第49研究所，黑龙江哈尔滨 150001；3.中国船舶重工集团公司第703研究所，黑龙江哈尔滨 150001)



基于相关向量机的氢气传感器故障恢复方法

王 冰1，2，张震宇3，刘 慧2,张洪泉1

(1.哈尔滨工程大学信息与通信工程学院，黑龙江哈尔滨 150001；2．中国电子科技集团公司第49研究所，黑龙江哈尔滨 150001；3.中国船舶重工集团公司第703研究所，黑龙江哈尔滨 150001)

在相关向量机回归模型的基础上，提出了一种新的氢气传感器故障数据恢复方法。利用小生境粒子群算法的“共享机制”对相关向量回归的核参数进行了优化，使其能快速准确地找到全局最优参数。用优化并训练后的回归模型对发生故障后的数据进行预测，实现故障恢复。将本文所用方法与其他较成熟的方法进行了比较，实验结果表明本方法在恢复准确度和鲁棒性方面均优于传统方法。数据恢复相对误差在±2.8%以内。

相关向量机；故障恢复；小生境粒子群算法；参数优化

0 引言

氢气(H2)是重要的化工原料，也是航天器发动机的主要燃料，在社会发展和提高国民经济中发挥着重要的作用[1-2]。氢气传感器作为氢气检测的主要手段之一，被广泛应用。然而，由于氢气传感器大多长时间使用，且工作环境恶劣，使故障发生的概率增大[3-4]。而且一旦发现故障，可能无法迅速更换。因此，对其进行故障状态监控及高效准确及时的故障数据恢复意义重大。

目前，国内外对传感器故障数据恢复的研究相对较少，大多集中在对故障状态的检测和诊断上[5]。传统的故障恢复方法主要有启发式搜索方法、数学优化方法、专家系统方法和神经网络等智能方法，但都存在结构复杂、实现困难以及收敛速度慢等各种问题[6-8]。支持向量机(Support Vector Machine，SVM)方法由于能够在较小的样本情况下，实现结构风险的最小化等优势，近年来被广泛研究，但其也存在着核参数设置复杂以及稀疏性有限等缺点[9-10]。针对这些问题，本文采用了相关向量机(Relevance Vector Machine，RVM)回归预测方法。RVM具备SVM的优点，且参数设置简单，核函数不受Mercer 条件限制，能够以概率形式给出输出结果，比SVM更具有稀疏性[11]。

在基于RVM的氢气传感器故障数据恢复方法中，核函数参数的选择对故障数据的恢复结果有很大的影响。针对这一问题，本文采用小生境粒子群优化算法对RVM的核参数进行优化，利用其"资源共享"的机制，快速获得RVM的最优参数，提高RVM回归模型的泛化精度，进而提高其恢复的准确度。

1 相关向量机回归原理

tn=y(xn;w)+εn

(1)

式中：εn服从均值为0，方差为σ2的高斯分布。

方差σ2一般可根据训练集目标值的噪声方差赋初值，通过数据训练迭代更新获取。监督学习模型可表示为：

(2)

式中:K(x,xi)为核函数;ωi为权重向量。

由于εn满足高斯分布，假设目标值tn独立同分布，则整个数据集的似然函数可表示为：

(3)

式中:t=(t1…tN)T;ω=(ω0KωN)T；Φ=[φ(x1),φ(x2),K,φ(xN)]T为N×(N+1)的矩阵；φ(xn)=[1，K(xn,x1),K(xn,x2),K,K(xn,xN)]T。

如果直接采用极大似然方法估计ω和σ2，可能会导致过适应，因此采用稀疏贝叶斯理论，定义高斯先验概率分布：

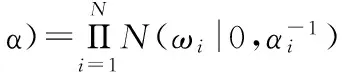
(4)

根据贝叶斯公式，所有未知参数的后验概率可以表示为：

(5)

式中：

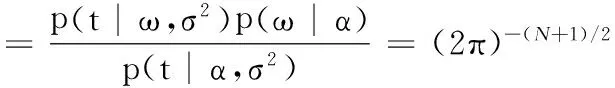
(6)

式中：∑=(σ-2ΦTΦ+A)-1；μ=σ-2∑ΦTt；A=diag(α0，α1，K，αN)。

用delta函数的峰值做近似运算，在一致超先验分布的情况下，p(t|α，σ2)可表示为：

(7)

使用迭代公式进行整理得：

(8)

(9)

式中:μi为式(6)中均值向量μ的第i个元素;γi=1-αiNii;Nii为式(6)中方差∑的对角线上的第i个元素。

这样，如果给定一个新的输入值x*，根据式(6)，预测值分布可以记为：

(10)

假设被积函数都满足高斯分布，因此预测值同样服从高斯分布，

(11)

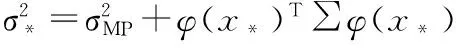
这样，RVM对新观测值的预测输出即为y(x*,μ)。

2 基于小生境粒子群算法的RVM参数优化

在RVM的回归模型中，核参数的选择会直接影响其回归的泛化性能，因此选择合适的参数是保证RVM 泛化精度的关键。传统的核参数选择方法往往是通过经验或遍历搜寻方法，具有一定的盲目性而且需要大量的时间，最后找到的参数也未必是全局最优解。针对这一问题，本文提出了一种基于小生境粒子群优化算法(NPSO)的RVM参数寻优方法，在传统粒子群优化算法中引入小生境共享机制，对核函数的带宽进行优化。小生境的共享机制增加了粒子种群的多样性，使其能够快速找到全局最优解。

传统的惯性权重PSO算法中，粒子的速度和位置按照如下公式更新：

vid(t+1)=wvid(t)+c1r1〔pbestid(t)-xid(t)〕+c2r2〔gbestid(t)-xid(t)〕

(12)

xid(t+1)=xid(t)+vid(t+1)

(13)

式中：i为第i个粒子；d为粒子维数；t为迭代次数；c1和c2为加速度常数;r1和r2是介于[0,1]之间的随机数;w代表惯性权重;xid代表粒子位置;vid代表粒子速度；pbestid是单个粒子i所经历的最好位置；gbestid是群体中所有粒子所经历的最好位置。

由于传统PSO算法容易出现早熟现象和陷入局部最优的问题，本文采用小生境粒子群算法对RVM参数进行优化。小生境粒子群优化算法是在传统PSO方法的基础上，引入了共享函数策略。共享函数代表了粒子之间的相似程度，通过它来调整群体中各粒子的适应度值，来增强种群的多样性，进而找到全局最优解。本文选择的共享函数如下式所示。

Sh(xj,xk)=‖xj-xk‖

(14)

式中：xj、xk表示两个不同的粒子。

如果两个粒子之间的距离小于某一给定距离S，用惩罚函数P乘以适应度值较差的个体的适应度值，来削减适应度值较差粒子的性能，使其适应度值更差。削减后的适应度函数为：

Fitness=Fitnessmax(xj,xk)×P

(15)

通过这种方式，在以后的迭代更新中淘汰适应度值更差的个体。由此，根据粒子之间的距离，调整群体中各粒子的适应度，使其之间保持一定的距离，保证了群体中个体的多样性，提高了收敛的速度。

NPSO算法的具体步骤如下：

(1)初始化种群的各参数以及各粒子的速度、位置；

(2)按适应度函数计算各粒子的适应度值，并计算两粒子间的共享函数值，若小于给定阈值S,用惩罚函数削减该粒子的适应度值，削减其性能；

(3)比较各粒子的当前适应度值及其所经历的最优适应度值，如果当前适应度值更小，将当前适应度值作为该个体所经历的最优适应度值；

(4)计算群体中所有粒子所经历的最优适应度值，讲其最小值作为全局最优适应度值；

(5)更新粒子的速度和位置，计算新的适应度值；

(6)如果达到最大迭代次数，停止更新，输出最优适应度值及其位置；否则转到(2)。

3 实验分析

3.1 基于NPSO的RVM回归参数优化

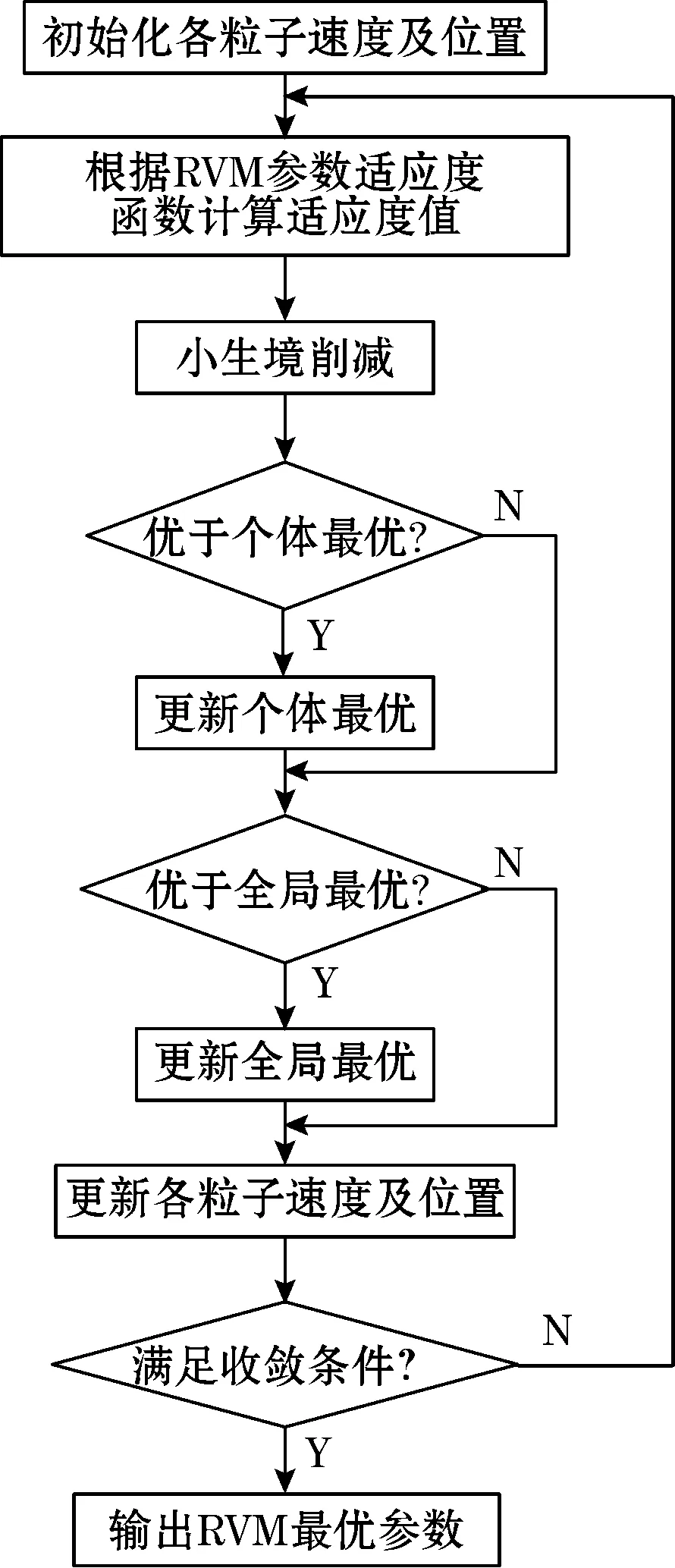
图1 NPSO方法对RVM参数优化流程图

根据上文所述原理，本文采用NPSO算法对RVM的回归参数进行优化。RVM参数的适应度函数是通过样本测试结果的均方根误差设置的，通过适应度函数来判断RVM的回归性能。如式(16)所示。

(16)

在RVM回归模型中，本文采用目前应用最广泛的高斯径向基核函数。因为只要参数选择合适，它可以适用于任意分布的样本。本文试验中，选取20组实验数据作为测试样本，NPSO算法的粒子数为30，最大迭代次数100次，初始权重w为1，加速度常数c1=c2=2，小生境距离常数S为1.5，惩罚因子P为1 000。参数优化过程的适应度值曲线如图2所示，在第62代以后，算法近似收敛于最优解，对应的RVM回归模型参数为σ2=1.4112。

图2 适应度值迭代曲线

3.2 基于RVM的故障数据恢复

根据分析，氢气传感器的气敏元件可能发生的故障有加热电极开路、短路；敏感膜开裂、脱落；零×10-7点满度漂移；多介质孔合闭；气敏材料自身结构变化等情况，这些故障可能会使传感器的输出值高于或低于测量范围，发生显著突变或恒值输出等。本文以传感器的输出值发生过载和突变的故障为例，利用得到的RVM最优参数，应用RVM回归模型对传感器的故障数据进行恢复，并取相同的测试样本和训练样本，与SVM、RBFNN方法进行了比较，如图3和图4所示。其中，RBF网络的输入节点数为2，隐层节点数采用自动确定的方法，输出节点数为1；SVM算法中选取径向基核函数，惩罚因子C=500，带宽σ2=1。

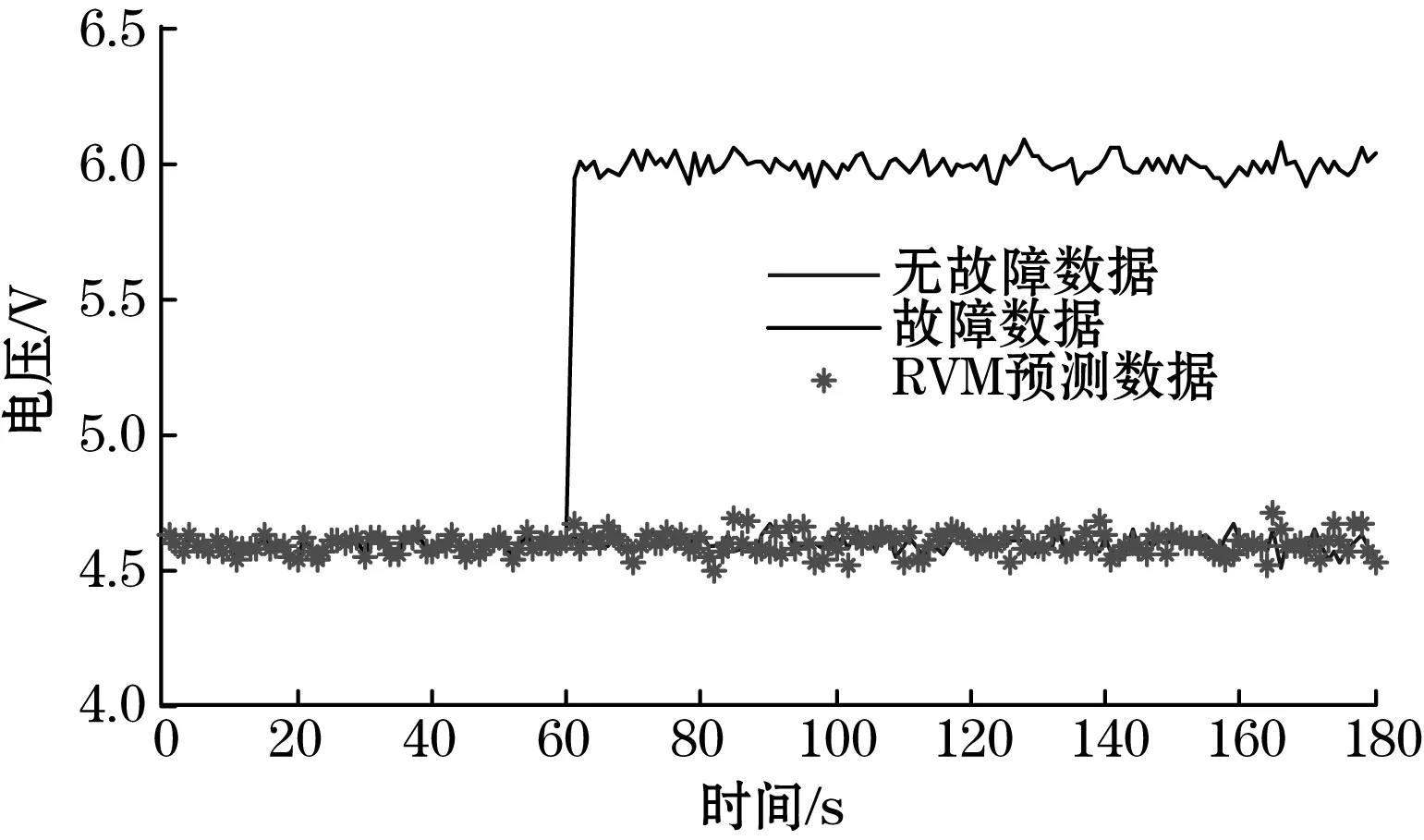
(a)

(b)

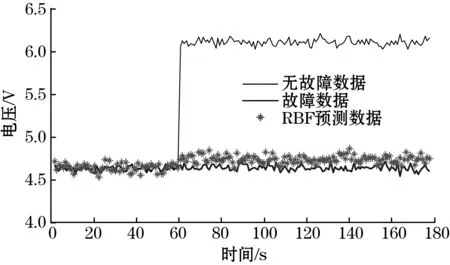
(c)图3 过载故障恢复曲线

从图3和图4可以看出，在过载和突变两种故障状态下，三种方法均能对故障数据进行恢复，但本文所用的方法在准确度上优于其它两种方法，且恢复数据的相对误差在±2.8%以内，验证了该方法的有效性，也说明了本文所用的方法具有良好的预测和推广能力。

4 结束语

本文针对氢气传感器故障恢复的问题，研究了一种基于RVM回归的故障数据恢复方法。该方法结合了小生境粒子群和RVM回归的优点，提高了RVM回归模型的准确率和传感器的稳定性，解决了现有氢气传感器发生故障后短时间内无法立即更换的问题，体现了传感器智能化的发展趋势。

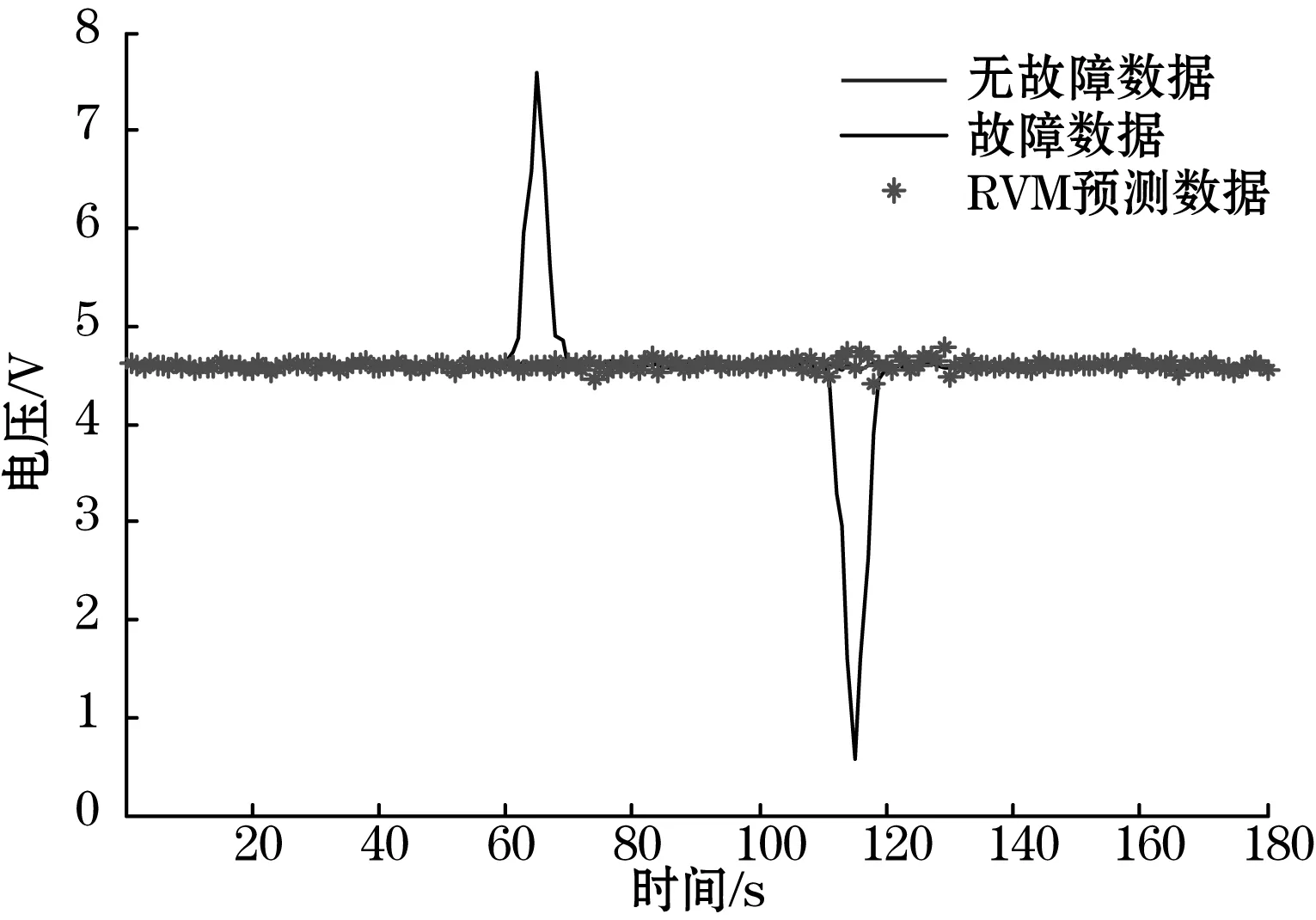
图4 突变故障恢复曲线

[1] WINTER C.Hydrogen energy-abundant,efficient,clean:A debate over the energy system of change.International Journal of Hydrogen Energy,2009,34:1-52.

[2] CLARK W W,RIFKIN J,O’Connor T,et al.Hydrogen energy stations:along the roadside to the hydrogen economy.Utilities Policy,2005,13(2):41-50.

[3] 王祁，赵树延，宋凯．多功能自确认传感器．传感技术学报，2011，24(4)：527-531．

[4] ELAOUD S,HADJ-TAIEB L,HADJ-TAIEB E.Leak detection of hydrogen natural gas mixtures in pipes using the characteristics method of specified time intervals.Journal of Loss Prevention in the Process Industries,2010,23(3):637-645.

[5] 申争光，朱凤宇，王祁.基于PFP-WRVM的多功能传感器状态自确认研究.仪器仪表学报,2012,33(9):1986-1994.

[6] 张美金，鄂小雪.基于改进LS-SVM的变压器油中气体浓度预测.仪表技术与传感器,2013(5):88-90.

[7] 范庚，马登武，邓力.基于灰色相关向量机的故障预测模型.系统工程与电子技术,2012,34(2):424-428.

[8] WANG W Q，GOLNARAGHI M F，ISMAIL F．Prognosis of machine health condition using neuro-fuzzy systems．Mechanical Systerns and Signal Processing,2004,18(4):1813-1831.

[9] 冯志刚，信太克规，王祁.基于最小二乘支持向量机预测器的传感器故障检测与数据恢复．仪器仪表学报,2007，28(2)：193-197．

[10] 马笑潇，黄席樾，柴毅．基于支持向量机的故障过程趋势预测研究．系统仿真学报，2002，14(11)：1548-1551．

[11] TIPPING M E.Sparse Bayes Learning and the relevance vector machine.Machine Learning Research,2001:211-244.

Fault Recovery Method of Hydrogen Sensor Based on Relevance Vector Machine

WANG Bing1,2,ZHANG Zhen-yu3,LIU Hui2,ZHANG Hong-quan1

(1. School of Information and Communication Engineering,Harbin Engineering Univ.,Harbin 150001,China;2. Chinese Electron Science and Technology Conglomerate 49th Research Institute,Harbin,150001,China;3. No.703 Research Institute of China Shipbuilding Industry Corporation,Harbin,150001,China)

Based on relevance vector machine regression model,a new fault data recovery method of hydrogen sensor was proposed in this paper. The “sharing mechanism” of niche particle swarm optimization algorithm was used to optimize kernel parameter of RVM,which can make it to find the global optimal parameter fast and exactly. The fault data were prognosed by using the regression model of optimized and trained to realize the fault recovery. The proposed method was compared with other mature algorithms,the results show that the proposed method is superior to the traditional ones in recovery accuracy and robustness．The relative error of fault recovery is within ±2.8%.

relevance vector machine; fault recovery; niche particle swarm optimization; parameter optimizing

2014-11-20 收修改稿日期：2015-07-04

TP206.3

A

1002-1841(2015)09-0011-03

王冰(1984— )，工程师，博士。主要研究领域:传感器信号检测、处理。E-mail：wangbing@hrbeu.edu.cn