时变时延离散网络控制系统的稳定性分析

刘 英 英

(沈阳大学 信息工程学院,辽宁 沈阳 110044)

时变时延离散网络控制系统的稳定性分析

刘 英 英

(沈阳大学 信息工程学院,辽宁 沈阳 110044)

研究了时变时延离散网络系统的稳定性问题.采用一个充分利用系统状态相关变量的Lyapunov泛函,应用牛顿-莱布尼茨公式并引入了松散变量技术,获得了新的基于线性矩阵不等式(LMI)的稳定性条件.此稳定性条件描述了网络状态相关变量之间的联系,且具有较小的保守性.仿真算例表明了所提出的方法的有效性.

时变时延; 离散网络系统; LMI

通过实时网络形成闭环的反馈控制系统称为网络控制系统(Networked Control Systems,简记为NCSs).随着计算机应用技术、网络技术和控制技术的飞速发展,网络控制系统受到了广泛的关注,并成为国际控制领域的一个研究热点.与传统的点对点结构的控制系统相比,NCSs具有成本低、安装与维护简便、可实现资源共享、易于扩展、高可靠性等优点[1].

网络控制系统虽然有如此多的优点,但是网络的引入也会给系统分析与综合带来新的挑战,如网络诱导时延、数据包丢失、数据包时序错乱、时变采样间隔、信号量化、宽带约束等.这些问题引起了许多学者的关注,然而如何对现有的方法进行改进或者提出新的研究方法来分析网络控制系统一直需要深入地探讨和研究[2].

网络中数据传输的过程中可能会产生一系列的问题,如网络诱导时延和数据丢包[3].网络诱导时延发生在网络中的传感器、执行器、控制器之间.在网络中存在时延的情况下,当控制参数改变时,被控量需要延迟一段时间之后才开始改变,使得被控量不能及时地响应控制信号的作用;由于时延的存在,控制信号不能立即抑制干扰.控制力的不同步实施,不仅降低了控制系统的性能,甚至会使系统不稳定.因此,稳定性问题是时延网络控制系统的主要研究内容之一[4-5].

当前,利用时滞系统方法研究具有时延的网络控制系统引起了许多学者的关注.在过去的几十年里,很多研究都集中到了连续网络控制系统的稳定性、控制器设计以及稳定化问题上[6-8].而对带时延的离散时间网络控制系统,虽然其有着很强的工程背景,但却没有得到足够的重视.

1 问题描述

考虑如下系统

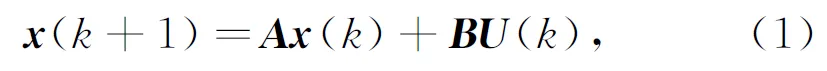
(1)

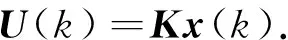
(2)

式中:x(k)∈Rn是状态;A,B是已知的具有适当维数的常数矩阵;U(k)是控制输入;K为状态反馈增益.

图1为一般的网络控制系统的结构.一个网络的闭环里,包括控制器、传感器、执行器,它们通过通信介质进行连接.控制器节点采用事件驱动,传感器节点和执行器节点采用时间驱动.传感器和执行器是同步的.设k1h为传感器侧的采样时刻,此时的状态为x(k1h).它经过d1(k)到达控制器,到达控制器的时刻为k2h.控制器输入信号经过d2(k)到达执行器,到达执行器的时刻为kh,则有

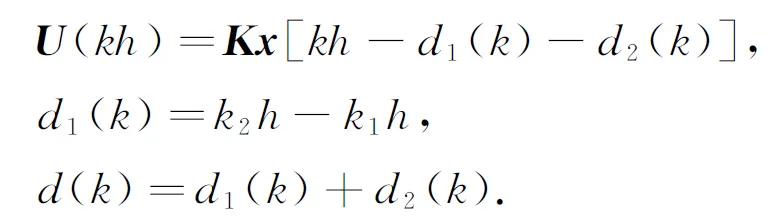
式中,k1,k2和d(k)都是整数;d1(k),d2(k)分别为传感器到控制器和控制器到执行器的网络诱导时延.

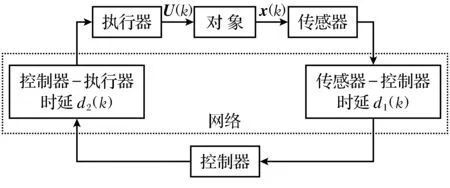
图1 网络控制系统的结构Fig.1 Structure of the network control system

假设网络诱导时延是时变的,且有界,满足如下条件

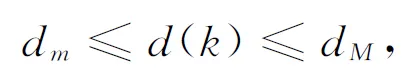
(3)

式中,dm和dM都是常数,分别表示时变时滞d(k)的下界和上界.

为了简单起见,下面用k1,k2,k分别替代k1h,k2h,kh.通过前面的分析,可以得到U(k)=Kx[k-d(k)].因此,在考虑网络诱导时延作用的情况下,闭环网络系统(1)和(2)可以表示为

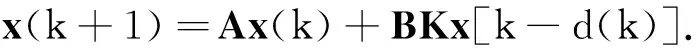
(4)

记Ad=BK,则系统(4)可以写成如下形式

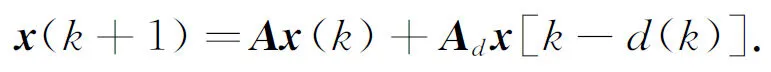
(5)

下面采用Lyapunov泛函方法,引入松散变量技术,并应用牛顿-莱布尼茨公式,给出系统(5)的新的稳定性条件.

2 主要结果

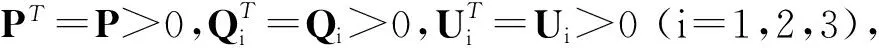
(6)

那么系统(5)在d(k)满足式(3)的条件下是渐近稳定的.式中

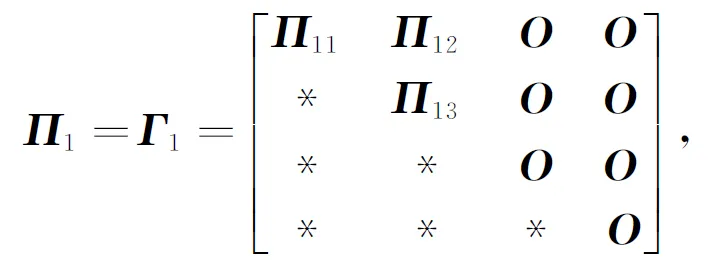
其中

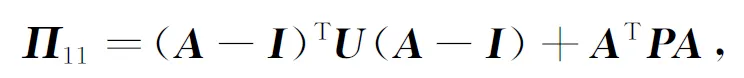
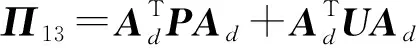
证明 定义η(k)=x(k+1)-x(k),并如下构建李雅普诺夫泛函

(7)

式中:

V1(k)=xT(k)Px(k),

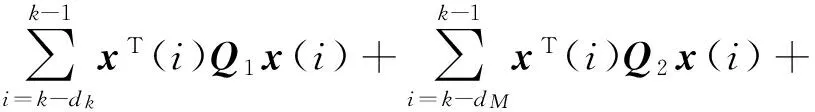
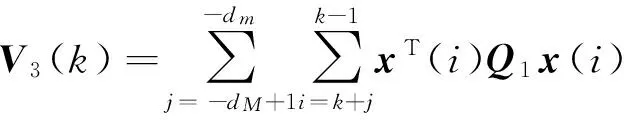
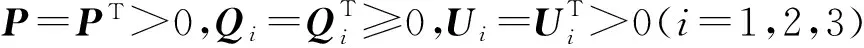
定义ΔV(k)=V(k+1)-V(k),则有:

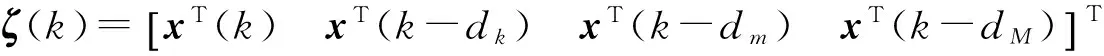
进一步可得

于是有

其中

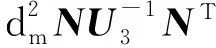
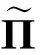
基于李雅普诺夫泛函方法,结合线性矩阵不等式方法和引入松散变量技术,获得了时变时延闭环网络系统(5)的稳定性条件,这里没有进行模型变化和使用有界方法.从定理的证明过程可以看出,所采用的的李雅普诺夫泛函没有忽略任何项,充分地利用了时滞的上界和下界的信息.

注:从定理的证明过程可以看出,矩阵变量Mi,Vi,Ni,Ti(i=1,…,4)分别用来表示x(k),x(k-dm),x(k-dM)和x(k+1)-x(k)这四项之间的关系.这些矩阵变量的引入可以使条件(5)变得更松散,这意味着在使用牛顿—莱布尼茨公式过程中引入这些变量是可以降低保守性的.下面的仿真算例也说明了这一结论.

3 仿真算例

下面通过仿真算例来说明本文所给出的方法要比现存的结果保守性要小.

例1[9]考虑如下系统模型:

(8)

式中,d(k)是时变的时延.当时延下界dm给定时,需要寻找最大的时滞上界dM,使得系统(1)和(2)保持渐近稳定.使用不同的稳定性判据得到的计算结果分列在表1中.从表1可以看出,定理的保守性比文献[2,9-11]的主要结果都要小.

表1 当dm不同时对应的时延上界Table1 The upper bound of delay correspondingto different dm

例2[12]考虑如下系统:

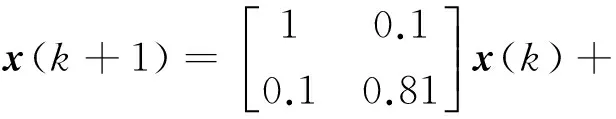
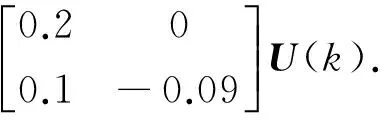
(9)

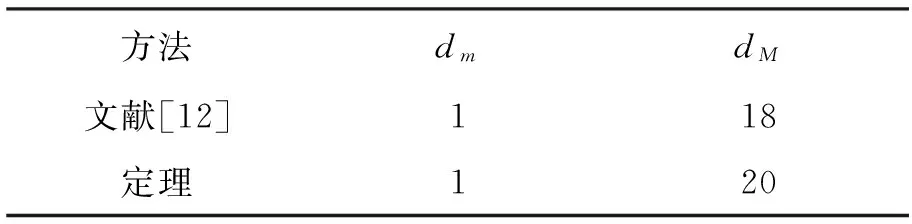
表2 在给定的控制器K的作用下获得的时延上界Table 2 The upper bound of delay obtained in the action of given controller K

从表2可以看出,本文的方法获得了更大的时延上界,这说明定理的保守性比文献[12]要小.图2表明了网络系统(1)和(2)在给定控制器作用下系统状态的变化过程.

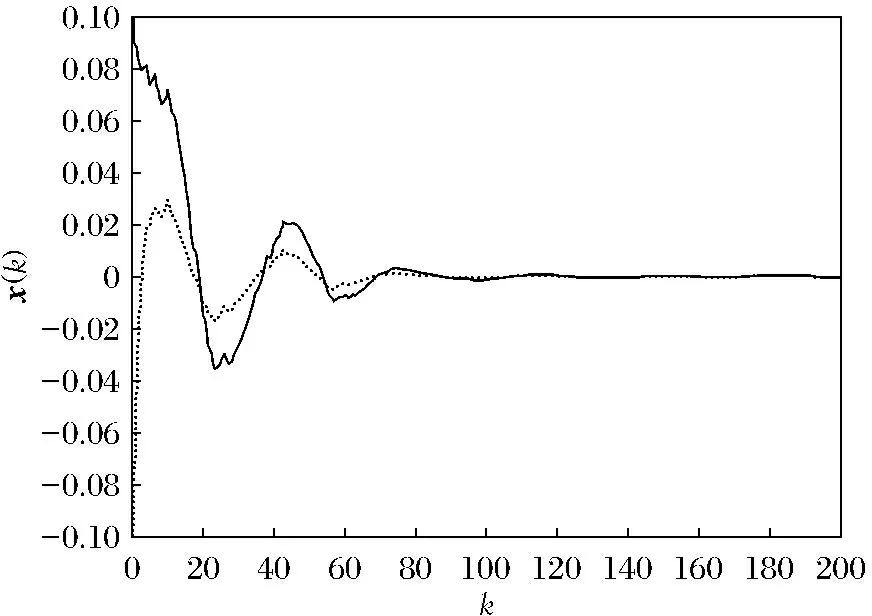
图2 系统状态响应曲线

Fig.2 Response curve of system state

4 结 语

本文研究了时变时延离散网络控制系统的稳定性问题,通过李雅普诺夫泛函方法,引入松散变量技术和应用牛顿-莱布尼茨公式方法,给出了基于线性矩阵不等式的稳定性条件.仿真算例也表明了所提出的方法相对于现有方法的有效性.

[1] Sun J D,Jiang J P.Delay and Data Packet Dropout Separately Related Stability and State Feedback Stabilisation of Networked Control Systems[J].IET Control Theory & Applications,2013,7(3):333-342.

[2] Sun L K,Wu J G.Schedule and Control Co-design for Networked Control Systems with Bandwidth Constraints[J].Journal of the Franklin Institute,2014,351(2):1042-1056.

[3] 苑旭东,张烁,井元伟.基于马尔科夫过程的单路由网络建模[J].沈阳大学学报:自然科学版,2012,24(4):45-48.

(Yuan Xudong,Zhang Shuo,Jing Yuanwei.Modeling of Single-Route Network Systems Based on Markov Processes[J].Journal of Shenyang University: Natural Science,2012,24(4):45-48.)

[4] Liu K,Fridman E,Hetel L.Stability andL2-gain Analysis of Networked Control Systems under Round-Robin Scheduling: A Time-delay Approach[J].Systems & Control Letters,2012,61(5):666-675.

[5] Peng C,Yang T C.Event-Triggered Commun-ication andH∞Control Co-Design for Networked Control Systems[J].Automatica,2013,49(5):1326-1332.

[6] Sun S L,Ma J.Linear Estimation for Networked Control Systems with Random Transmission Delays and Packet Dropouts[J].Information Sciences,2014,269:349-365.

[7] Hui G T,Zhang H G,Wu Z N,et al.Control Synthesis Problem for Networked Linear Sampled-Data Control Systems with Band-Limited Channels[J].Information Sciences,2014,275:385-399.

[8] Zhang X M,Han Q L.Event-Triggered Dynamic Output Feedback Control for Networked Control Systems[J].IET Control Theory & Applications,2014,8(4):226-234.

[9] Gao H J,Chen T W.New Results on Stability of Discrete-time Systems with Time-Varying State Delay[J].IEEE Transactions on Automatic Control,2007,52(2):328-334.

[10] Zhang B Y,Xu S Y,Zou Y.Improved Stability Criterion and its Applications in Delayed Controller Design for Discrete-Time Systems[J].Automatica,2008,44(11):2963-2967.

[11] Zhu X L,Yang G H.Jensen Inequality Approach to Stability Analysis of Discrete-Time Systems with Time-Varying Delay[C]∥Proceedings of 2008 American Control Conference.Washington,2008:1644-1649.

[12] Tian E G,Yue D,Zhao X.RobustH∞Control for Discrete-Time Network-Based Control Systems[C]∥Proceedings of the 6th World Congress on Intelligent Control and Automation.Dalian,2006: 344-348.

【责任编辑: 李 艳】

Stability Analysis for Discrete-Time Networked Control Systems with Time-Varying Delay

LiuYingying

(School of Information Engineering,Shenyang University,Shenyang 110044,China)

The problem of stability for discrete-time networked control systems with time-varying delay was studied.By using Lyapunov functional approach,which take full advantages of state related variables,applying Newton-Leibniz formula and introducing loose variables technology,the sufficient conditions for stability analysis in term of linear matrix inequalities (LMI) were given.The results of stability analysis for the systems descript the relationship of system state related variables and it is less conservative than the existing results.A numerical example was also presented to illustrate the effectiveness of the developed method.

time-varying delay; discrete-time networked control system; linear matrix inequalities (LMI)

2015-01-13

国家自然科学基金资助项目(61104106); 辽宁省教育厅资助项目(L2014480).

刘英英(1980-),女,辽宁葫芦岛人,沈阳大学讲师,博士.

2095-5456(2015)04-0301-05

TP 273.5

A