服务管理目标优化配置的Fuzzy-QFD线性规划模型构建与求解

陈知然, 于丽英

(上海大学 管理学院,上海 200444)



服务管理目标优化配置的Fuzzy-QFD线性规划模型构建与求解

陈知然, 于丽英

(上海大学 管理学院,上海 200444)

由于服务管理的复杂性和模糊性，现有方法难以有效解决基于主观语言评价的服务质量改进问题。本文拓展了质量功能展开(QFD)方法在服务业中的应用，通过构建一个模糊线性规划模型，以求解最大化提高顾客需求综合满意度的企业能力优化配置问题。首先基于顾客感知-期望差距的模糊评估确定顾客需求、需求权重和边界约束等模型参数，接着运用模糊线性回归和非对称三角模糊数的隶属函数，将含有模糊变量的模糊线性规划问题转化为经典线性规划问题，进而求得不同模糊条件下的模型解。最后通过网购平台的实例验证了模型的有效性和可行性。

管理科学；优化配置；Fuzzy-QFD；模糊线性规划,非对称三角模糊数；服务管理

0 引言

质量功能展开(Quality function deployment，QFD)方法是把顾客或市场的需求(“什么”)转化为设计要求、工程特性和管理能力(“如何”)的多层演绎分析方法。随着服务经济的发展和QFD研究的深入，QFD方法被应用于服务业。与可由标准刻度指标衡量的产品质量不同，服务评价取决于人类的主观判断。人类主观判断具有模糊不清的特点，会使多样性条件下的日常决策产生失真，采用模糊多属性的三角模糊数来量化难以捉摸的、模糊的语言信息是一个有效方法[1]。因此，在涉及服务管理时，研究人员倾向于运用模糊质量功能展开方法(Fuzzy-QFD)[2]，其本质是把顾客需求和工程特性之间模糊的定性和定量信息转化为直观的数学矩阵，再基于数学矩阵构建数学模型。

不同条件下Fuzzy-QFD数学模型构建和求解存在一定的困难性[3]。因此，在现有的研究中，大部分文献运用相对简单的模糊排序和模糊比较方法判定工程特性的重要性；而像Chen等[4]和施洪国等[5]基于顾客需求和工程特性之间模糊函数关系，构建相对复杂的模糊规划模型求解工程特性目标水平的文献还较少见。文献[4]和[5]为构建和求解复杂Fuzzy-QFD数学模型提供了有效方法，推动了Fuzzy-QFD研究的发展,但还有进一步拓展的空间：(1)模型运算基于对称三角模糊数，而在群体决策中对个体的评估结果加权平均后，时常会出现非对称三角模糊数，需要改进原有线性规划模型的求解方法；(2)模型构建时未深入研究服务管理和QFD的特征，顾客需求和相关需求参数由专家给出而非顾客评价；(3)模型目标是求解理想状态下工程特性的目标值，实际中用于实现工程特性的资源往往有限且要考虑管理的经济效益，因此，工程特性配置度的优化研究也是一个重要课题。

综合考虑上述问题，根据QFD方法在服务管理中的应用特征——把企业能力作为满足顾客需求的工程特性[6]，本文基于顾客的模糊评价确定顾客需求、需求权重和边界约束，构建一个优化企业能力配置、实现顾客需求综合满意度最大化的模糊线性规划模型，并提出利用非对称三角模糊数的隶属函数关系求解模糊线性规划模型的方法，以得到最大化提升顾客需求综合满意度的企业能力配置度。

1 模糊线性规划模型构建及求解

1.1 三角模糊数和隶属函数概念

模糊数是定义在实数域上的一类特殊的模糊集。

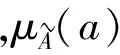
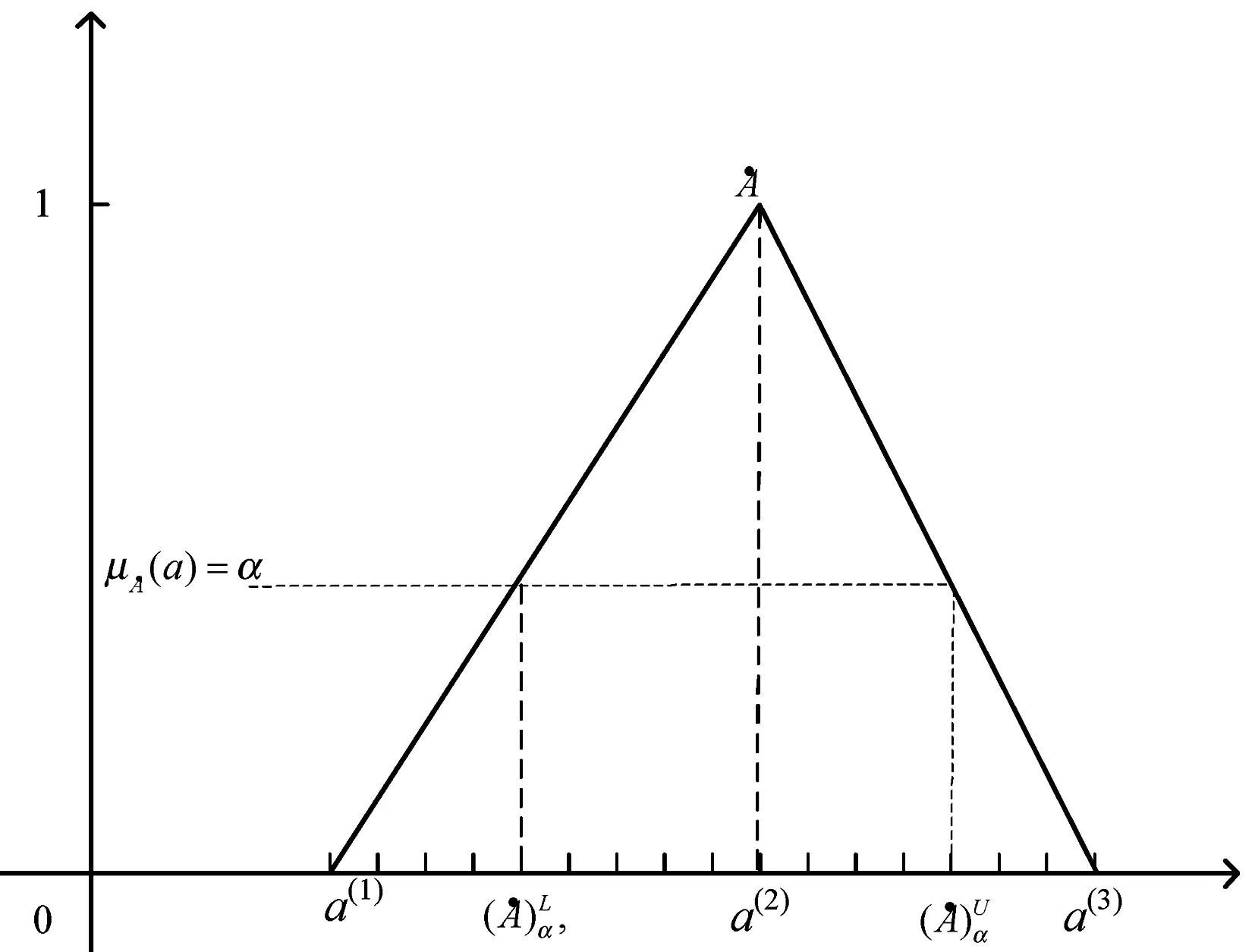
图1 三角模糊数的隶属函数

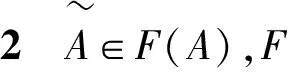
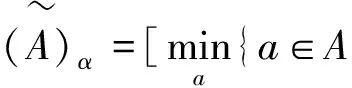
(1)

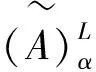
1.2 模糊线性规划模型的构建

文献[4]和[5]基于顾客需求和工程特征的相关性构建了产品质量管理的模糊线性规划模型，本文将该模型推广到服务质量管理，从求解产品质量工程特征的目标值，拓展到研究最大化满足顾客需求的企业能力优化配置问题。根据Fuzzy-QFD的建模方法，假设有M个顾客需求(“什么”)和N个企业能力(“如何”)，定义yi(i=1,2,…,M)为第i项顾客需求的满意度，xj(j=1,2,…,N)为第j个企业能力的配置度，Z(y1,y2,…,yM)为顾客需求综合满意度的提高水平，是实际管理效果同期望管理效果的比值。基于QFD在服务业中的应用，构建一个通过优化企业能力配置度以求最大化提高顾客需求综合满意度的模糊线性规划模型：

(2a)

约束条件：

yi=fi(x1,x2,…,xN),i=1,2,…,M

(2b)

xj=gj(x1,…,xj-1,xj+1,…,xN),j=1,2,…,N

(2c)

yimin≤yi≤yimax,i=1,2,…,M

(2d)

其中，fi表示顾客需求和企业能力之间的函数关系，gj表示不同企业能力相互间的函数关系，θi为顾客需求权重，yimin,yimax为yi的边界约束，即最小值和最大值。

1.3 模型参数的评估与确定

QFD的核心思想是以市场为导向，以顾客为依据，从顾客那里获得的信息越多，管理效果越好。因此在服务管理中，顾客需求i(i=1,2,…,M)和需求权重θi及边界约束yimin、yimax的具体参数要源于顾客的模糊评价，而非管理专家设定。

顾客评价服务质量的好坏取决于“感知得到的服务”和“期望获得的服务”的比较[9]，因而，通过比较基于L个需求因素的顾客感知P和顾客期望E的评价数值，可以确定M项顾客需求，M≤L。需求因素是专家团队设计的参考因素，应尽可能全面地概括顾客关注的服务内容。

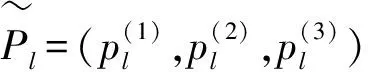
(3a)

(3b)

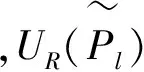
(4a)

(4b)

(4c)

(4d)

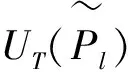
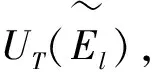
(5)

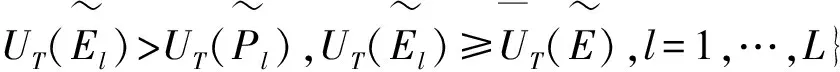
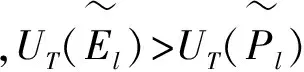
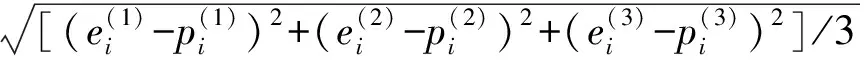
(6)

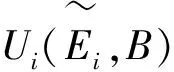
(7)

其中，UT(B)是最高语言评级对应的三角模糊数在公式(3b)中的计算结果。基于以上分析对需求权重θi进行定义：

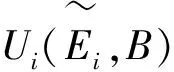
(8)

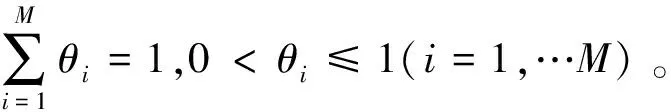
运用综合效用函数法和顶点坐标法，可减少因使用单一方法造成的失真现象，使需求权重θi更加准确。

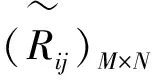
1.4 模糊数学模型向经典模型的转变

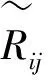
(9)

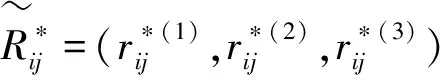
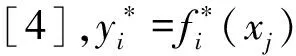
(10)

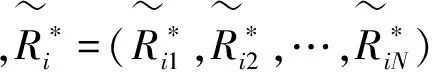
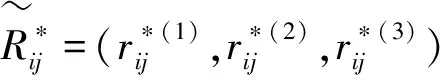
(11)

(12)

根据公式(12)及定义3中顾客需求满意度的边界约束，把模糊等式约束转化为经典不等式约束：

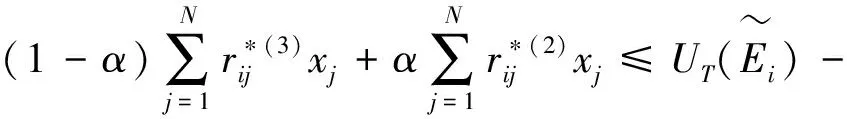
(13)

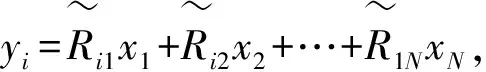
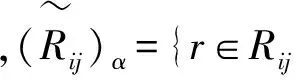
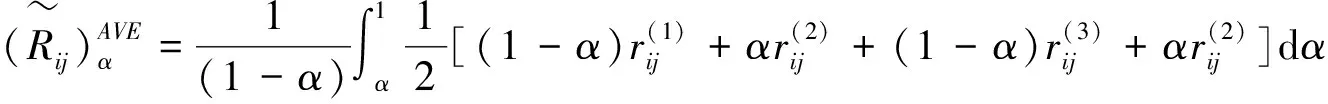
(14)

实现约束条件和目标函数的转化后，将模糊数学模型转变为给定α阈值的确定性线性规划模型：

约束条件：

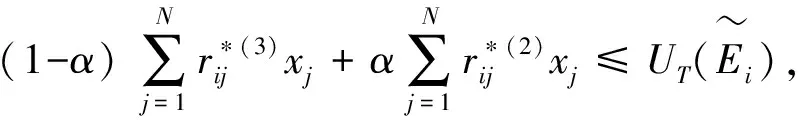
(15)

2 实例

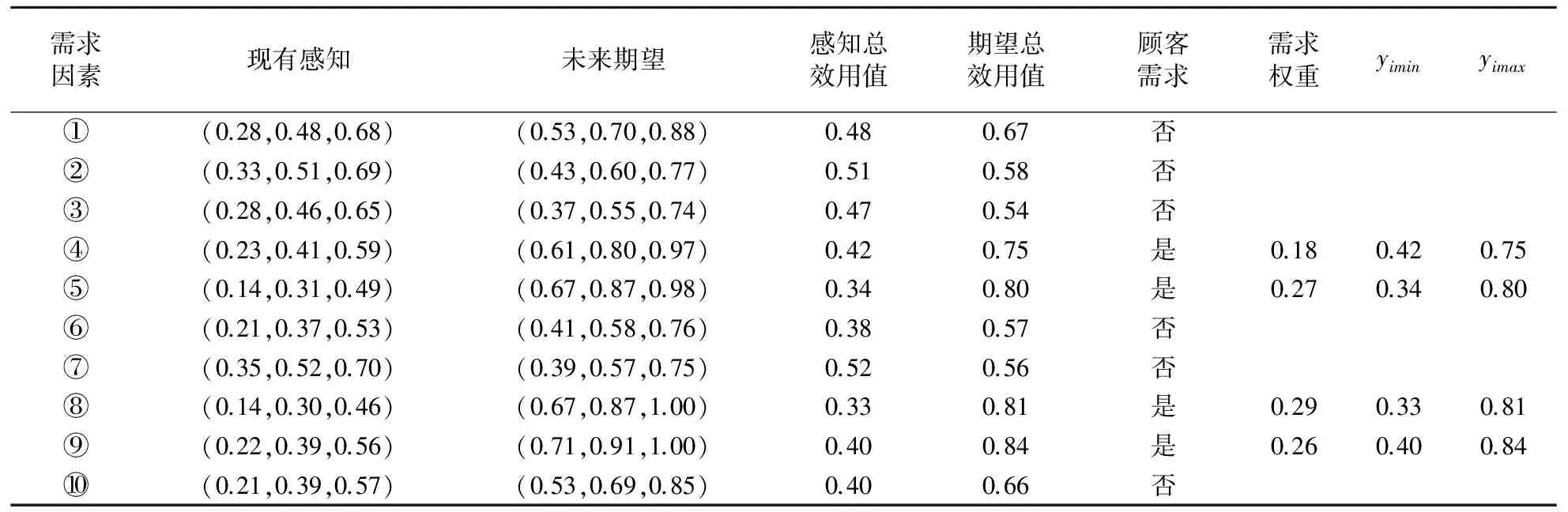
表1 基于顾客感知-期望差距比较获得的模型参数

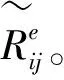
(16)

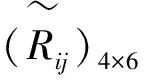
maxZ=1.01x1+0.33x2+1.12x3+1.05x4+0.6x5+1.04x6-0.87

约束条件：

运用Matlab求解线性方程，获得给定阈值的模型解，见表2。

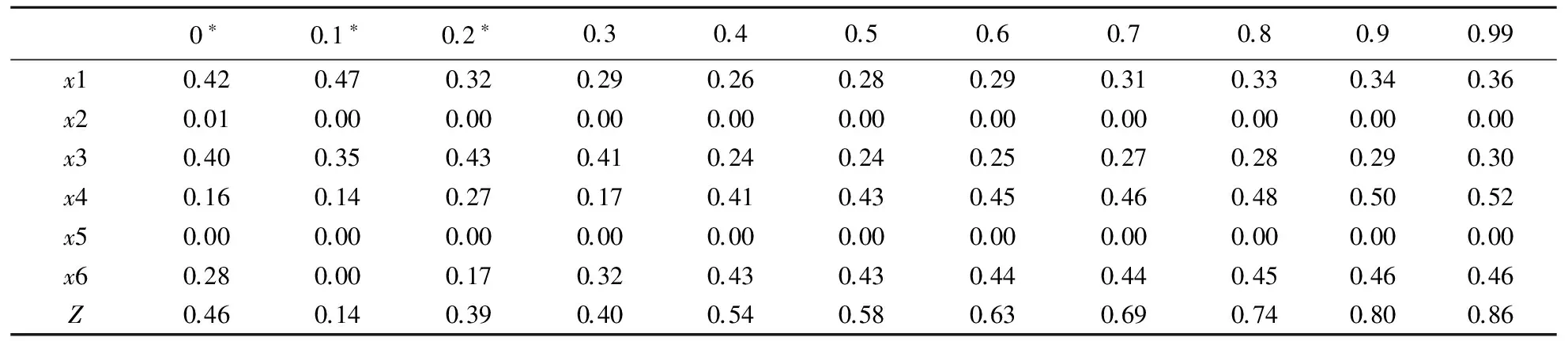
表2 基于给定α阈值的模型解

注：*为Matlab求出的近似解。

在特定的模糊性下，按照表2中企业能力的配置度，实现了顾客需求综合满意度的最大化提升。如α=0.6时，以0.29：0.25：0.45：0.44的配置比例组合顾客沟通、宣传推广、技术保障和日常管理能力用于服务管理，可实现最大化提升顾客需求的综合满意度，实际管理效果同期望管理效果的比值达为0.63，表明这种配置水平最具经济效益。α阈值表示信息的主观性和模糊性，确定合适的α阈值是一项重要而艰难的工作。并且在信息的模糊度非常高的情况下，模糊线性方程可能只求得近似解(带*的阈值)。当α≥0.3时，随着模糊性的减弱，管理信息逐渐明晰，顾客需求综合满意度的提高水平Z会增大。

3 结论

本文构建了基于Fuzzy-QFD的模糊线性规划模型，用于研究服务管理中顾客需求和企业能力之间的转化关系；并运用多种方法把模糊数学模型转变为给定α阈值的确定性线性规划模型，从而求得模型解。针对语言评估的模糊特性和群体决策产生的非对称三角模糊数问题，本文在模型构建和求解时提出了一些新方法：采用模糊的顾客感知-期望差距比较方法确定顾客需求、需求权重及边界约束等模型参数，从而避免了在模型设计阶段的信息丢失；通过融合企业能力的自相关性和顾客需求与企业能力相关性简化了约束条件运算，运用模糊线性回归方程和非对称三角模糊数的隶属函数将模糊等式约束转化为经典不等式约束；并把目标函数中的非对称三角模糊数转化为不同α-截集水平下的模糊区间，通过定积分的方法求解α-截集区间内所有元素的平均值，实现目标函数的去模糊化。

通过Matlab软件的程序运算，可获得不同α阈值的企业能力的配置度。关于如何选择合适的α阈值，这是Fuzzy-QFD及其它模糊集理论应用中遇到的普遍性难题，也是我们未来的研究方向。

[2] 洪志生，苏强霍，佳震.服务质量管理研究的回顾与现状探析[J].管理评论，2012,24(7):152-163.

[3] Carnevalli J A, Miguel P C. Review, analysis and classification of the literature in QFD-types of research, difficulties and benefits[J]. International Journal Production Economics, 2008, 114(2): 737-754.

[4] Chen Y, Chen L. A Non-linear possibilistic regression approach to model functional rolationships in product planning[J]. International Journal Advanced Manufacture Technology, 2006, 28(11-12): 1175-1181.

[5] 施国洪，韩淑粉，徐胜男.基于模糊非线性回归的QFD目标水平决策模型[J].统计与决策，2011,16:47- 49.

[6] Bottani E, Rizzi A. Strategic management of logistics service: a fuzzy QFD approach[J]. International Journal Production Economics, 2006, 103(2): 585-599.

[7] 胡宝清.模糊理论基础[M].武汉：武汉大学出版社,2004.

[8] Kao C, Liu S-T. Fractional programming approach to fuzzy weighted average[J]. Fuzzy Sets and Systems, 2001, 120(3): 435- 444.

[9] Grönroos C. An applied service marketing theory[J]. European Journal of Marketing, 1982,16(7): 30- 41.

[10] Cochran J K, Chen H N. Fuzzy multi-criteria selection of object-oriented simulation software for production system analysis[J]. Computers and Operations Research, 2005, 32(1): 153-168.

[11] Hsieh C H, Chen S H. A model and algorithm of fuzzy product positioning[J]. Information Sciences, 1999, 121(1-2): 61- 82.

[12] Chen C T. Extensions of the TOPSIS for group decision-making under fuzzy environment[J]. Fuzzy Sets and Systems, 2000, (1): 114, 1-9.

[13] Fung R Y K, Tang J, Tu Y, Wang D. Product design resources optimization using a nonlinear fuzzy quality function deployment model[J]. International Journal of Production Research, 2002, 40(3): 585-599.

[14] Oussalah M. On the compatibility between defuzzification and fuzzy arithmetic operations[J]. Fuzzy Sets and Systems, 2002, 128(2): 247-260.

[15] Cass A, Carlson J. An empirical assessment of consumers’ evaluations of web site service quality: conceptualizing and testing a formative model[J]. Journal of Services Marketing, 2012, 26(6): 419- 434.

[16] Yoo B, Naveen D. Developing a scale to measure the perceived quality of an internet shopping[J]. Quarterly Journal of Electronic Commerce, 2001, 2(1): 31- 46.

[17] Liu C T, Timon C D, Tsai H. A study of the service quality of general portals[J]. Information & Management, 2009, 46(1): 52-56.

[18] Parasuraman A, Zeithaml V A, Berry L L. SERVQUAL: a multiple-Item scale for measuring consumer perceptions of service quality[J]. Journal of Retailing, 1988, 64(1): 12- 40.

[19] Tang J, Fung R Y K, Xu B. A new approach to quality function deployment planning with financial consideration[J]. Computers and Operations Research, 2002, 29(11): 1447-1463.

Structure and Solution of a Fuzzy-QFD Iinear Programming Model for Objective Optimal Allocation in Service Management

CHEN Zhi-ran, YU Li-ying

(ManagementofSchool,ShanghaiUniversity,Shanghai200444,China)

The exiting methods are difficult to solve improvement problems of service quality under subjective linguistic evaluation effectively, because of the complexity and fuzziness of service management. In this study, we expand the application of quality function deployment(QFD)to structure a fuzzy linear programming model, to solve the problem of optimized allocation of limited company capabilities for satisfying customer requirement to the maximum. Firstly, the paper identifies model parameters of customer requirement, requirement weight and requirement bounded constraints on the basis of fuzzy evaluation of comparison of customer perception and expectation. Secondly, fuzzy linear regression and membership function of the asymmetric triangular fuzzy number are used to transform fuzzy linear programming problem with fuzzy variables into a classical linear programming problem in order to obtain the model solutions under different fuzzy conditions. Finally, an example of online shopping is provided to demonstrate the effectiveness and feasibility of the proposed method.

management science; optimal allocation; Fuzzy-QFD; fuzzy linear programming; asymmetric triangular fuzzy number; service management

2013-12-23

国家自然科学基金资助项目“基于QFD的模糊MDO建模与优化方法研究”(71272177)

陈知然(1982-)，男，博士生，浙江温州人;于丽英(1969-)，女，通讯作者，博士生导师，教授，浙江湖州人。

F284

A

1007-3221(2015)06- 0128- 08

10.12005/orms.2015.0204