基于功率谱密度的静电悬浮加速度计分辨率估计方法

刘 爽，刘云峰，董景新

(清华大学精密仪器系，高精度导航技术教育部重点实验室，北京 100084)



基于功率谱密度的静电悬浮加速度计分辨率估计方法

刘 爽，刘云峰，董景新

(清华大学精密仪器系，高精度导航技术教育部重点实验室，北京 100084)

高精度静电悬浮加速度计常采用功率谱密度估计(PSD)来评估分辨率水平，商用PSD分析仪需实时在线分析，且分析时间长、频域分辨率低、成本高。为此提出了一种线下PSD估计方法，利用简易采集系统采集噪声信号，再进行PSD估计。给出了正确的PSD估计表达式，推导了加速度计分辨率与PSD的关系，通过实验对比了该方法与HP35670A动态分析仪分析结果，实验结果验证了该方法的有效性。最后用该方法分析了研制的静电悬浮加速度计原理样机X1、Y和Z2三个通道加速度噪声的PSD，得到0.1 Hz处PSD分别为：8.07×10-5g/Hz1/2、3.29×10-8g/Hz1/2和2.39×10-7g/Hz1/2；在带宽0.001～0.1 Hz内分辨率分别为4.64×10-5g、4.21×10-8g和1.51×10-7g。

功率谱密度估计；维纳辛钦定律；Welch法；静电悬浮加速度计

0 引言

空间应用的静电悬浮加速度计广泛应用在卫星精密定轨、重力场测量及等效性原理验证等空间应用领域[1-3]，在0.1 mHz～0.1 Hz测量带宽内，噪声水平可达10-7～10-14g/Hz1/2。其原理为通过检测悬浮质量块的位移变化产生控制电压，控制电压与预载电压生成静电力与外界惯性力平衡，则施加的控制电压可反映输入加速度的大小。控制电压噪声属于平稳随机信号，地面实验时可通过分析控制电压噪声的PSD来评价加速度计分辨率[2,4-5]，将PSD在相应带宽内积分便可得到这一带宽内噪声水平。

采用商用仪器进行PSD估计时需要实时在线分析，分析时间长、频域分辨率低、成本高，且只能估计电压信号。为此本文提出了一种线下PSD估计方法，利用LabVIEW编写的采集程序和数字万用表组成简易采集系统长时间采集加速度计控制电压信号，再利用MATLAB进行PSD估计。采集到离散的噪声信号方法相对简单，关键是如何根据采集的离散数据获得真实的PSD。对PSD定义文献中不统一[6-7]，只有与噪声对应的PSD估计表达式才能反映真实噪声水平。文献[7-8]对PSD表达式做了修正，但未说明与噪声水平的关系，也没有通过实验验证PSD估计正确性。为此本文重点分析了信号分辨率、标准差与PSD关系，给出PSD估计的标准表达式，并给出利用MATLAB计算PSD的方法，利用该方法与HP35670A动态分析仪结果进行对比，验证方法的有效性，最后利用上述方法对本实验室研制的静电悬浮加速度计进行PSD估计。

1 静电悬浮加速度计工作原理

如图1所示，检测质量与电极构成差动电容，依靠检测电路和反馈电路产生静电力将检测质量悬浮在电极框中心，反馈电压大小反映了外界输入加速度大小。检测质量与周围电极共形成6对差动电容，可实现3个平动和3个转动的六自由度测量。

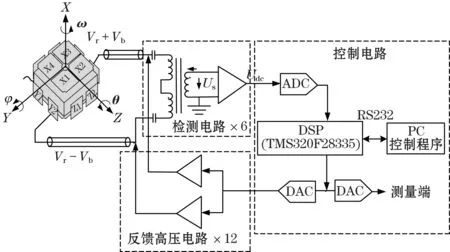
图1 静电悬浮加速度工作原理

实际测量加速度可表示为

am=ain+adtb=KscalVb

(1)

式中：am为测量加速度，可根据标度因子Kscal和控制电压Vb计算；ain为实际加速度；adtb为加速度噪声，由地基振动噪声、电路噪声、表头金丝噪声、轴间耦合噪声等因素组成。

因此加速度计分辨率被噪声所限制，尤其是地基振动噪声影响[9]。可根据加速度计噪声水平估计地面实验能够达到的分辨率。

2 数据采集系统及PSD估计原理

利用LabVIEW编写的数据采集程序，实现数字万用表与计算机的串口通信，构成简易数据采集系统，采集噪声数据，再利用MATLAB编程进行PSD分析，原理如图2。LabVIEW数据采集程序主要利用"VISA Serial"模块配置串口波特率等信息，利用串口写和串口读模块对串口进行操作。

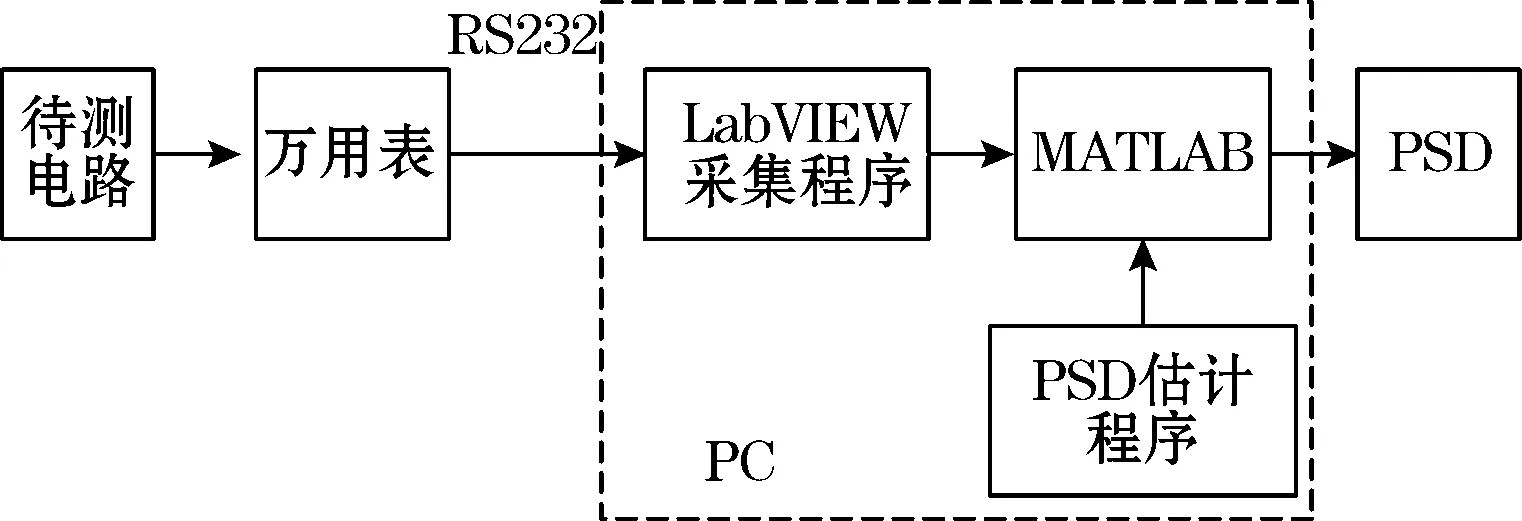
图2 简易PSD估计原理

为准确给出静电悬浮加速度计分辨率与PSD关系，有必要对相关原理进行推导。

2.1 功率谱、某一点实际功率与PSD关系

通常采用单一样本、有限N个数据做功率谱估计，如式(2)所示[6,10]：

(2)

按照式(2)定义，功率谱的求法是将采样得到的离散数据x(n)做FFT得到X(k)，再求其模的平方除以采样点数N作为功率谱的近似估计[10]，即：

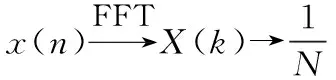
(3)

式中SNd为双边功率谱，实际物理系统负频率没有实际意义，通常定义单边功率谱SNs，其表达式如下：

(4)

设离散信号x(n)=Asin(2πfkn/Fs)，Fs为采样频率，FFT得到的fk处频域幅值X(k)与时域幅值A关系为

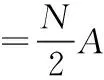
(5)

系数2是因为FFT后得到的为双边幅值谱。设P(k)为频率点fk处真实功率，在fk处时域功率与频域功率应该相等，且功率以有效值的平方表示，即：

(6)

对比式(4)，可知SNs(k)与P(k)关系为

(7)

即k点处单边功率谱为实际功率的N倍。

PSD定义为单位带宽内的功率。若幅值单位为V，则PSD单位为V2/Hz或V2/rad，如式(8)所示：

(8)

式中：Δf为频率间隔，即频率分辨率；ΔP为这一带宽内的功率，对于PSD为定值且连续的平稳随机信号。

可知频率间隔Δf越大，ΔP越大，二者相除结果保持不变。又由频率分辨率表达式Δf=Fs/N可知，对于平稳随机信号PSD与采样频率和采样点数无关。

对于频谱是线谱的周期信号，如正弦信号，其功率在特征频率f0处有最大值，远远大于附近频率功率，这一频率间隔内的功率等于正弦信号功率，因此在f0附近，正弦信号PSD值随频率间隔增大而减小，所以周期信号不适合做PSD分析[4]。

联立式(6～8)可得PSD表达式为：

(9)

其中，假设N为偶数，k=0～N/2，即PSD等于fk处功率除以频率分辨率，也等于功率谱除上采样频率。

国际上通常采用PSD的算术平方根值root PSD表示PSD[2,4]，即：

(10)

若x(n)为单位为g，则root PSD单位为g/Hz1/2。

2.2 自相关函数、总功率及均方值的关系

广义平稳、各态遍历的离散随机信号的数字特征均可以用单一样本的时间平均代替集总平均，其自相关函数rx(m)、总功率Pm和均方值Ψ2(x)定义分别为[6]：

(11)

(12)

当m=0时，联立式(11)和式(12)有如下关系式成立：

(13)

平稳随机信号可以看成无限个不同频率、不同幅值的正弦信号叠加，因此对于离散正弦序列上述关系仍然成立。

2.3 信号噪声标准差与PSD关系

由维纳-辛钦定理[6,10]可知功率信号x(n)的自相关函数和功率谱是一对傅里叶变换对，即：

(14)

当m=0时，由式(13)、式(14)得：

(15)

即该平稳随机过程的自相关函数在m=0点取值等于总功率、等于均方值，也等于功率谱在整个带宽内积分。

又由数理统计原理可知，对于平稳随机序列，有均方值等于方差减去均值的平方，即：

(16)

当信号均值为零时，即μx=0，有:

(17)

方差的平方根即为信号标准差，常用来衡量信号噪声水平。

因此对于功率谱在(-π,π)内积分除上2π等于信号的总功率，也等于零均值信号的方差，反映的这一频带内噪声大小。维纳-辛钦定理对于周期信号也成立[11]，周期信号频谱在频域上为离散谱。

式(15)中Sx(ejω)为功率谱，Sx(ejω)/(2π)应为PSD，且为双边PSD，因此有：

(18)

令ω=2πk/N，则：dω=2πdk/N，其中dk=1，代入式(15)得：

(19)

即PSD对带宽(-π,π)内积分结果为信号总功率。

若采用真实频率f来表示PSD，由角频率与实际频率关系[6]：ω=2πf/Fs，代入式(15)得：

(20)

式中Sf(ej2πf/Fs)/Fs为按照式(9)定义的PSD值，即：

(21)

又由fk=kFs/N，得df=Fsdk/N，代入式(20)得：

(22)

即PSD对整个实际频率内积分结果为总功率值。

结合式(15)、式(17)和式(22)得：

(23)

即对于均值为零的平稳随机信号，整个频带内PSD积分结果与总功率、均方值以及方差(标准差平方)相等。

采用式(23)给出的PSD值，对PSD在整个频带积分，或者直接从PSD图上用PSD平均值乘上对应带宽，就得到这一带宽内的总功率，开方后即可得到噪声标准差，直观地估算噪声水平。若PSD计算方法选取不恰当，会造成积分结果不等于方差值，得不到真正的噪声水平。

若求均值为零、带宽为f1～f2频率段内信号噪声水平为

(24)

若采用root PSD表示，式(24)修正为

(25)

即根据root PSD图，将其值平方后与带宽相乘，再开方便可估算这一频带内噪声水平。

3 PSD估计方法选择及分析工具

式(9)给出了PSD求取方法，即利用FFT求取x(n)的离散傅里叶变换X(k)，取其模平方除上归一化系数,再乘以2倍换成单边谱表达式，最后再除以采样频率Fs。也等于功率谱除以采样频率。式(9)称为周期图法PSD估计。

功率谱估计方法有经典和现代估计法，经典的功率谱估计方法主要有周期图法、自相关法及韦尔奇法(Welch法)；现代功率谱估计法有ARMA模型、AR模型、MA模型等[6]。对于平稳随机信号，不同方法得到的功率谱只是分辨率和标注差上差异，积分后得到的噪声水平不会有数量级上的差别。这里以经典功率谱分析法中Welch法和周期图法为例分析。

3.1 Welch法功率谱估计法

设数据x(n)长度M=N×L，N为每一个分段区间长度，L为分段数(窗长度)，则Welch法功率谱估计为[12]：

(26)

(27)

式中ωn为使用的窗函数。

当窗函数为矩形窗时：

(28)

(29)

将式(26)除以采样频率Fs，并乘以2倍，并联立式(28)、式(29)得：

(30)

对比式(30)和式(9)，可见式(30)得到的是一个分段数据长度N上的周期图法单边PSD的估计。若再按照式(27)平均，得到的便是Welch法单边PSD估计即：

(31)

若采用窗函数是其他窗，如汉明窗，有：

(32)

(33)

可证明仍然有：

(34)

即分子分母由于加入窗函数而引入的比例系数一致，近似互相抵消。虽然加窗会引起PSD值在某一点处存在误差，但整个带宽内积分仍然为渐进无偏估计。

3.2 MATLAB自带PSD估计函数

进行PSD估计时，即可按照式(9)利用FFT编程计算，也可以利用MATLAB(7.1版本)自带的PSD函数进行分析。MATLAB采用Welch法进行PSD估计的命令主要有"pwelch"和"psd"，利用周期图法进行PSD估计的命令为"periodogram"。其中"pwelch"和"periodogram"内部算法是按照式(30)和式(31)来计算的，而函数命令"psd"给出的是双边功率谱，应按式(35)修正得到PSD[7]：

(35)

采用上述函数对白噪声进行PSD估计，结果如图3，图中纵坐标采用root PSD表示,N=2 048，Fs=1 024 Hz，矩形窗；Welch法分段长度N/4，段重叠率0.5。按式(25)积分求总功率结果见表1。

图3 不同方法计算白噪声PSD结果

pwelchperiodiagrmimprovedpsd数理法0.082730.082310.082750.08236

由图3可知，"pwelch"和"psd"由于采取分段处理，窗口长度M小于数据长度N，使得PSD分辨率下降，但PSD方差性能得到改善，曲线起伏变小。周期图法PSD估计，分辨率高但方差性能不好，因此Welch法PSD估计是牺牲分辨率换取方差性能的改善。由表2可知，三种方法求得的整个带宽内功率与数理统计方法得到功率(方差)近似相等。综合考虑，Welch法估计的PSD方差性能得到了很好改善，可以增大点数克服分辨率下降影响，只要积分后总功率偏差在允许范围内，Welch法PSD估计得到比较好的估计结果，因此采用MATLAB命令"pwelch"进行Welch法PSD估计。

4 实验研究

4.1 PSD估计方法正确性验证

为验证上述PSD分析方法的正确性，对检测电路输出电压噪声进行PSD分析，分别采用上述方法(以下简称"Welch法")和HP35670A动态分析仪(以下简称"HP35670A")PSD分析结果进行对比，如图4所示。图中，HP35670A线数M=1600，fBW=1.562 5 Hz；Welch法采样点数N=4 096×3,Fs=4 Hz，分段长度(窗口长度)分别为N/3，段重叠率0.5；二者均采用矩形窗，频率分辨率均为9.77×10-4Hz。HP35670A给出0～fBW内PSD，Welch给出0～Fs/2内PSD。

图4 Welch法和HP35670A计算PSD结果对比

由图4可知，在同样采样频率下，采用不同方法得到的PSD值在低频段(f<0.5 Hz)十分吻合，因此在我们关心的0.001～0.1 Hz带宽内采用Welch法可以得到真实的PSD；在频率大于0.5 Hz时Welch法得到的PSD略小于HP35670A得到的值，这可能是万用表采样频率不够高的原因。

将图4中PSD值在0.001～0.5 Hz内积分比较其总功率值，并与方差对比。需要注意的是Welch法进行PSD前先去除均值，HP35670A积分时去除第一个直流量数据点。结果如表2。可见，不同方法在相同带宽内得到的总功率与数理法求得的方差十分接近，计算偏差没有数量级的差异，因此偏差不会影响噪声估计水平。因此本文提出的简易PSD估计方法能够对噪声进行PSD估计，反映真实噪声水平。

表2 不同方法得到的总功率对比 V2

4.2 静电悬浮加速度计X1、Y、Z2向PSD估计

采用上述方法对实验研制的静电悬浮加速度计加速度噪声进行PSD估计，X1、Y、Z2三个通道加速度噪声PSD分析结果如图5所示。图中，Fs=1 Hz,N=1 024，分段数N/2，段重叠率0.5，矩形窗。

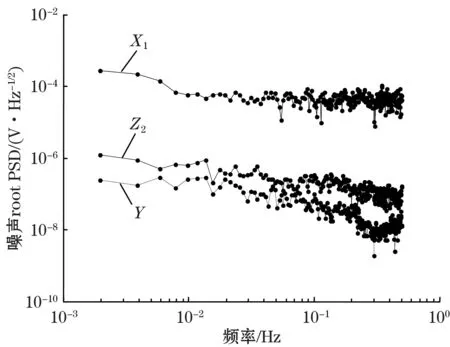
图5 静电悬浮加速度噪声PSD

由图5可见，由于竖直X方向为高压悬浮方向，加速度噪声PSD最大，水平敏感方向Y/Z噪声较小。将加速度PSD在相应带宽内积分，求取噪声的标准差，即反映加速度计的分辨率，结果如表3所示。可见目前我们实验室研制的静电悬浮加速度计原理样机的水平Y向加速度噪声水平在0.1 Hz处为3.29×10-8g/ Hz1/2，在0.001 Hz～0.1 Hz分辨率4.21×10-8g，更高精度的静电悬浮加速度计正在研制当中。

表3 静电悬浮加速度计不同轴噪声性能比较

5 结论

本文提出了一种简易PSD估计方法，重点对噪声PSD与加速度计分辨率关系进行了详细推导，给出了PSD正确计算公式和计算方法，通过与HP35670A动态分析仪PSD估计结果对比，验证了该方法的有效性。相比于商用仪器，该方法具有成本低，可线下处理，可获得更高频率分辨率，可分析非电压信号的PSD等优点。

最后利用该方法对静电悬浮加速度计原理样机加速度噪声进行了分析，得到了X1、Y和Z2通道PSD在0.1 Hz处分别为：8.07×10-5g/ Hz1/2、3.29×10-8g/ Hz1/2和2.39×10-7g/ Hz1/2；在带宽0.001～0.1 Hz内对PSD积分得到加速度分辨率分别为4.64×10-5g、4.21×10-8g和1.51×10-7g。

[1] WISE J O,BURKE W J,SUTTON E K.Globally averaged exos- pheric temperatures derived from CHAMP and GRACE accelero- meter measurements.Journal of Geophysical Research:Space Physics,2012,117(A4):A04312.

[2] TOUBOUL P,FOULON B,CHRISTOPHE B,et al.CHAMP,GR- ACE,GOCE Instruments and Beyond.Geodesy for Planet Earth,2012,215-221.

[3] BOCK H,JAGGI A,BEUTLER G,et al.GOCE:precise orbit deter- mination for the entire mission.Journal of Geodesy,2014,88(11):1047-1060.

[4] 薛大同.静电悬浮加速度计噪声测试数据的频谱分析方法.空间科学学报,2008,28(1):55-63.

[5] 胡广书.数字信号处理.北京:清华大学出版社,2003:470-496.

[6] 赵若红，傅继阳，吴玖荣，等.Matlab内建psd函数在工程随机振动谱分析中的修正方法.暨南大学学报：自然科学版,2007,28(5):435-439.

[7] 彭兢，金长江.在 MATLAB 中模拟平衡随机过程.北京航空航天大学学报,2001,27(5):585-588.

[8] ZHOU Z B,LIU L,TU H B,et al.Seismic noise limit for ground -based performance measurements of an inertial sensor using a torsion balance.Classical and Quantum Gravity,2010,27(17):175012.

[9] HAYES M H.Statistical digital signal processing and modeling.John Wiley & Sons,1996:95-99.

[10] 徐科军，黄云志，林逸榕，等.信号分析与处理.北京:清华大学出版社,2006:191-194.

[11] WELCH P D.The use of fast Fourier transform for the estimation of power spectra:a method based on time averaging over short,mod- ified periodograms.IEEE Transactions on audio and electroa- coustics,1967,15(2):70-73.

Method for Resolution Estimation of Electrostatically SuspendedAccelerometer Based on Power Spectrum Density (PSD)

LIU Shuang,LIU Yun-feng,DONG Jing-xin

(MOE Key Laboratory for High-precision Navigation Technology,Department ofPrecision Instruments,Tsinghua University,Beijing 100084,China)

Power spectrum density (PSD) estimation is always used to evaluate the resolution of electrostatically suspended accelerometer(ESA).Commercial instrument for the PSD estimation need online estimating，and there are some other shortcomings,such as low frequency resolution and high cost.So a simple method for PSD estimation was proposed.The theory and formation of the method were given,so was the relation between PSD and resolution of ESA.The results of PSD,which were got by this method and HP35670A dynamic analyzer,show that this method was valid.At last,the PSD inX1,YandZ2channels of ESA using this method was evaluated.The noise PSD at 0.1 Hz are 8.07×10-5,3.29×10-8and 2.39×10-7g/Hz1/2,respectively.The resolution in the 0.001～0.1 Hz are 4.64×10-5g,4.21×10-8gand 1.51×10-7grespectively.

power spectrum density estimation;Wiener-Khinchin theorem;welch method;electrostatically suspended accelerometer

清华大学自主科研计划(20091081243)

2014-12-03 收修改稿日期：2015-07-28

U666.1

A

1002-1841(2014)10-0030-05

刘爽(1985—)，博士研究生，主要从事空间高精度静电悬浮加速度计关键技术研究。E-mail：345196170@qq.com