振动主动控制中加速度信号的积分方法

王 震，孙玉东

(中国船舶科学研究中心船舶振动噪声重点实验室，江苏无锡 214082)



振动主动控制中加速度信号的积分方法

王 震，孙玉东

(中国船舶科学研究中心船舶振动噪声重点实验室，江苏无锡 214082)

在采用速度反馈的振动主动控制系统中，利用DSP系统对加速度信号进行时域积分获得速度信号。速度反馈振动主动控制系统采用的速度信号相位必须准确，为获取正确的速度信号，提出了积分初值的确定方法，在不采用滤波的情况下，将积分结果减去其均值实现了直流量和趋势项的去除。在DSP系统中验证了该方法的有效性，积分得到的速度信号的幅度和相位与实际值保持一致。

振动主动控制；加速度；数值积分；速度反馈

0 引言

机械系统中，表征系统振动的物理量有加速度、速度和位移。在许多振动测试系统中，由于受到环境和传感器安装条件的限制，位移和速度无法测量，此时需要通过对加速度信号积分获得速度信号获得速度信号[1-2]。在建筑结构的半主动控制中，多以结构的速度反应作为状态反馈，但是工程实际中会出现测量不准以及误差积累等问题[3]。而采集振动加速度信号简单且可靠，因此常采用通过加速度信号进行积分得到速度信号[4]。对加速度信号进行积分有硬件积分和软件积分2种方法。硬件积分所存在的问题是积分后的信号精度会下降，幅值和相位得不到保证，甚至产生畸变[5]。软件积分分为时域积分和频域积分，频域积分算法复杂，运算量大，在控制系统中可能造成较大的时延，不满足系统实时性的要求。因此研究并实现加速度信号的实时时域积分具有重要的现实意义。

在直接速度反馈控制系统中使用的速度信号需要与实际的速度信号相位保持一致，因此在积分过程中需要确定速度信号的初值，文中对此提出了积分初值确定的方法。在积分的过程中，由于传感器信号中的直流分量的影响，积分所得的速度信号会含有一次趋势项。传统的趋势项去除的方法有高通滤波法、EMD分解法和曲线拟合法[6]。高通滤波会导致积分得到的速度信号的相位滞后[7]，EMD分解法和曲线拟合法不满足实时性要求，均会造成控制系统不稳定。系统通过求取积分所得速度信号的均值实现一次趋势项的去除，试验结果证实该系统能够获得正确的速度信号。

1 加速度信号的数值积分

1．1 数值积分

设振动加速度信号为a(t)，则振动速度信号为

(1)

式中：v′(t)为v(t)的原函数；v0为初始速度。

数值积分的公式有很多，常用的有梯形公式，辛普森公式和牛顿-柯特斯公式。由于数值求积公式的阶数越高，积分所得结果的精度越高，因此选择三阶多项式进行加速度信号的积分。令加速度信号的采样值为a(i)(i=1，2，…，n)；通过对当前的加速度值和以前的加速度值拟合得到当前的速度增量dvi[8]，即：

(2)

式中：α0=T/24；α1=-5T/24；α2=19T/24；α3=9T/24；T为系统的采样间隔。

当前时刻的速度通过下式计算：

vi=vi-1+dvi

(3)

根据递推关系得速度值的递推公式如下：

(4)

1．2 速度初值的确定

在速度反馈振动主动控制系统中需要获得正确的速度信号，就需要获得正确的速度初值。对于单频信号，加速度为极大值时刻的速度值为零，这样可以间接得到速度信号的初值，然而对于多频信号和宽带信号则不能采用该方法。现有文献往往没有探讨初值确定的方法。

对式(1)左右两侧求均值，并取离散形式，可以得到：

(5)

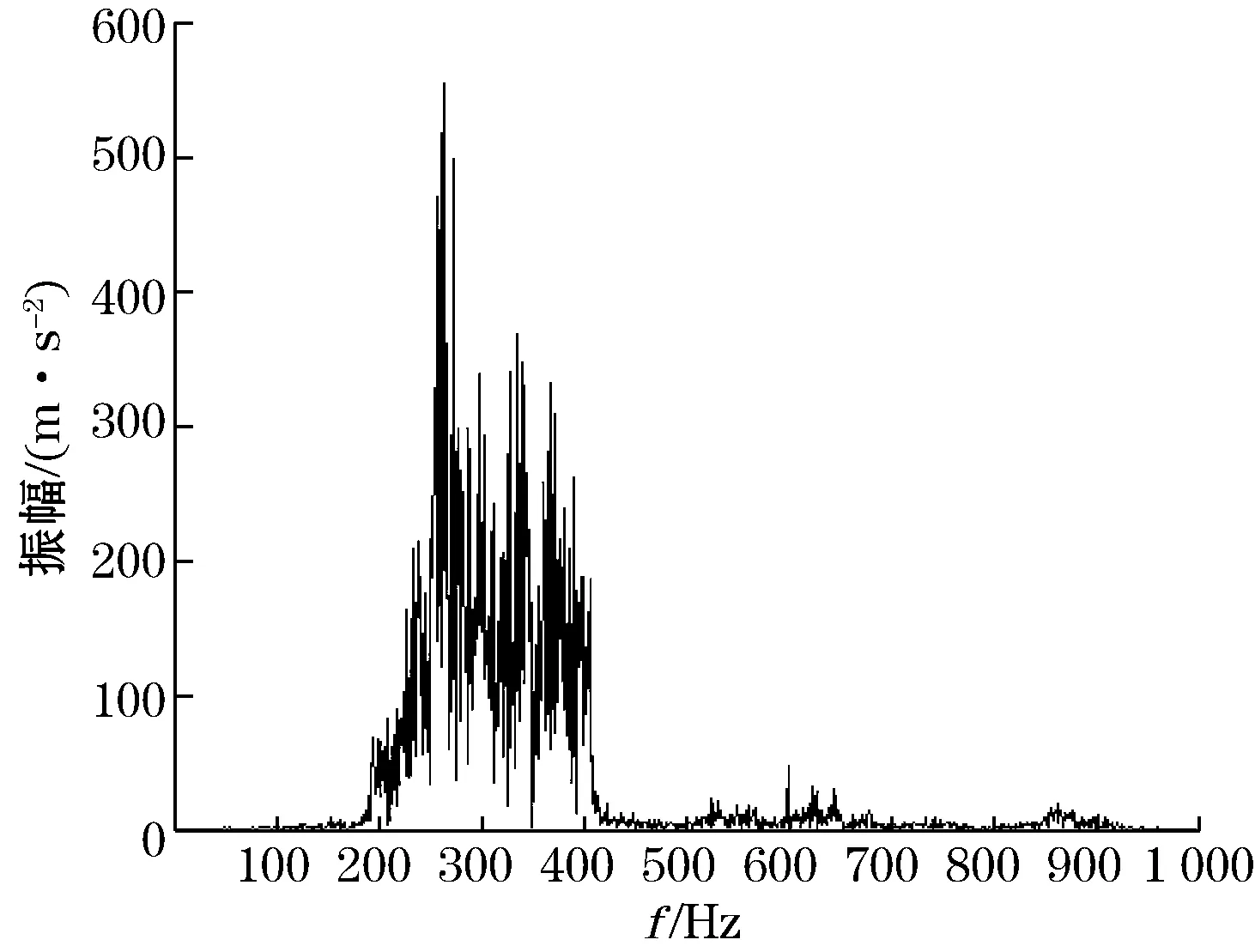
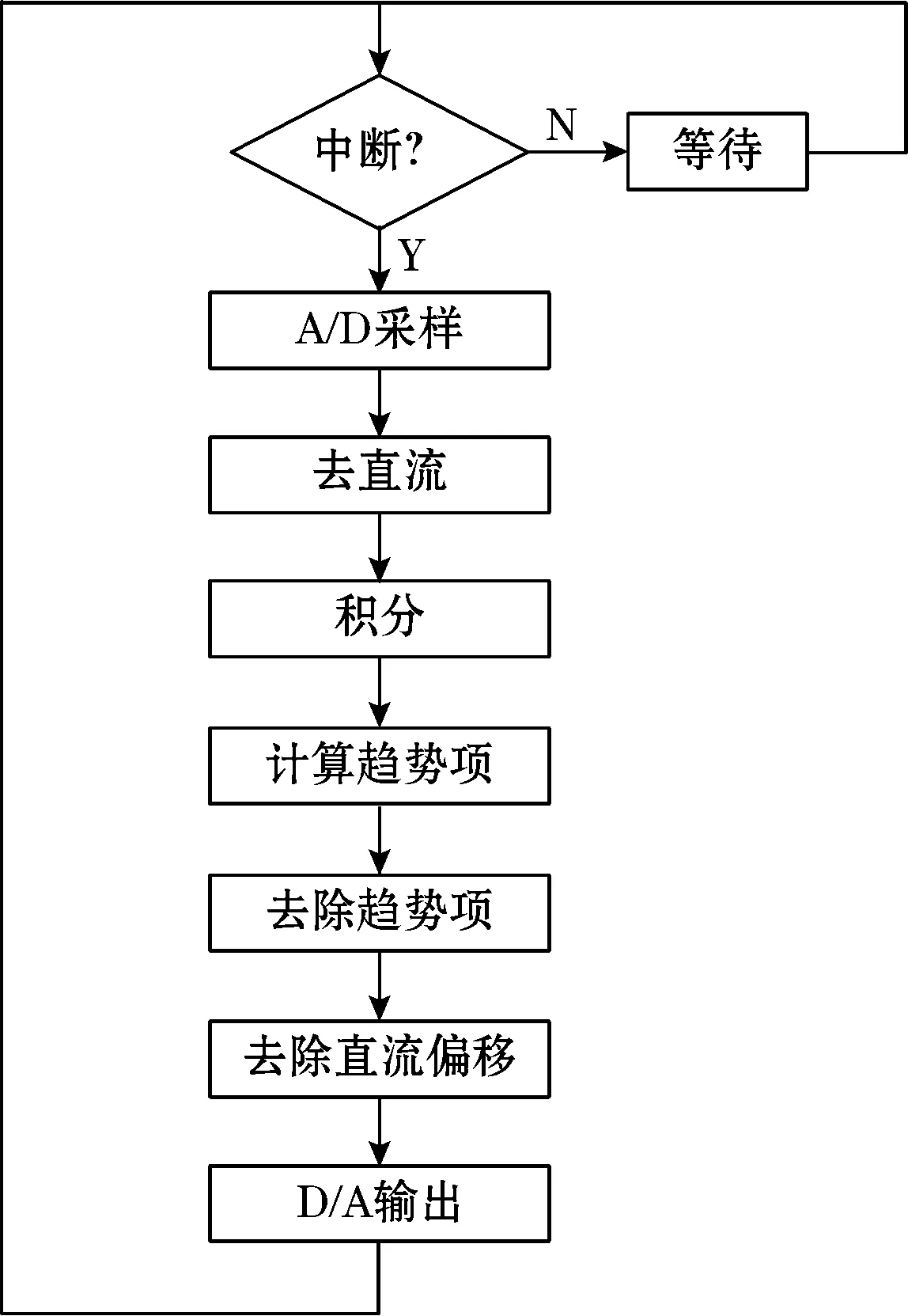
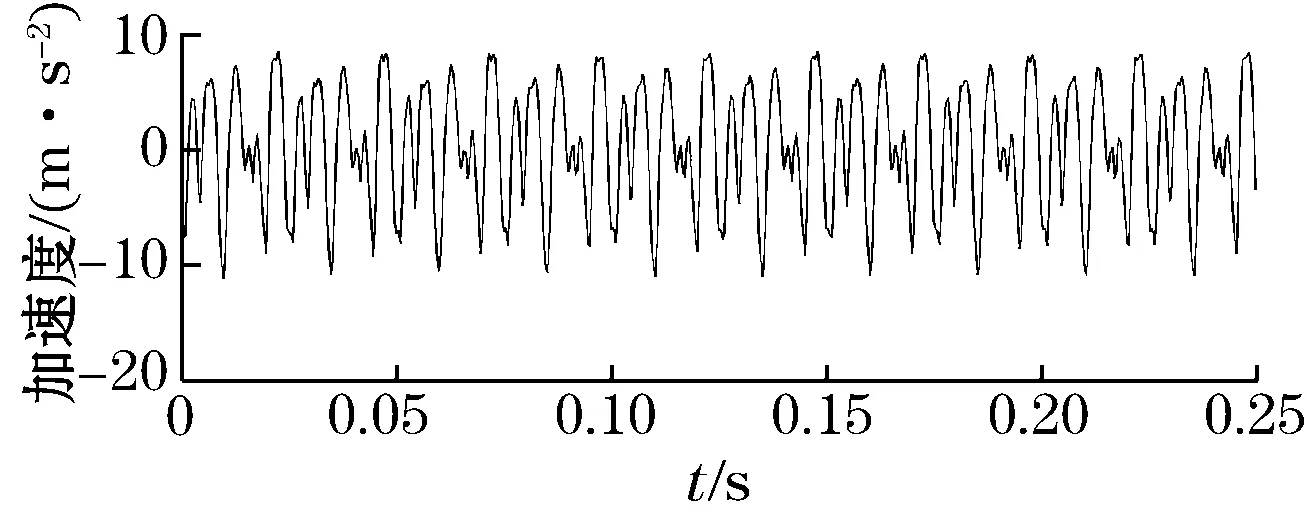
由于在实际的振动系统中，振动信号由不同频率的正弦信号组成，因此整周期的速度信号的均值为零。设速度信号1个周期有n个采样点，对N个速度信号取均值，令N=an+b，且0

(6)

(7)

(8)

2 趋势项及其消除

实际的系统中，采样得到的振动加速度信号含有直流分量，即a(t)=a′(t)+ε，加入直流分量之后，式(1)和式(4)分别变成

(9)

(10)

式(10)中，直流分量随着积分产生的累积量iTε称为趋势项。产生趋势项的原因是多样的，主要包含几个方面：

(1)传感器的零点漂移；

(2)信号采集系统采集的信号的直流量[9]；

(3)加速度信号中含有极低频的噪声信号，没能经过高通滤波器完全滤除。

由于直流分量和趋势项的存在，导致实际积分结果的误差很大，需要进行软件修正，去除直流量和趋势项才能得到正确的振动速度信号。

目前常用的去除趋势项的方法主要有高通滤波法，EMD分解法和拟合多项式3种方法。高通滤波会改变速度信号的相位信息，造成控制系统不稳定。EMD分解法算法复杂，运算量大，不适合应用于实时控制系统。多项式拟合存在的问题是需要合理地设置每一次进行多项式拟合所用的数据点的数目，这需要一定的经验，通常反复操作才可以取得一个最优的结果[10]，这也限制了其不能应用于实时控制系统。文中通过求取速度信号的均值从而间接获得趋势项并对其进行消除。

N个由式(10)计算得到的速度信号的均值为

(11)

(12)

将式(12)代入式(11)可得：

(13)

3 DSP系统软件流程

控制系统主控芯片为数字信号处理器TMS320F2812.该型DSP为32位定点DSP，系统工作频率最高可达150 MHz．A/D转换器为AD7656，该款A/D转换器芯片集成了6个16位精度的A/D转换器。D/A转换器为AD5754，该款D/A转换器芯片集成了4个16位精度的D/A转换器。

图1为DSP系统运行的程序的流程图，该程序的核心是加速度信号的一次积分。使用DSP的定时器0产生中断信号，系统接受中断申请之后驱动AD7656对电荷放大器输出的加速度信号进行采样。通过设置定时器0的计数值可以控制中断系统产生中断的时间间隔，进而实现所需要的采样频率。系统采样频率设置为10 kHz。

图1 DSP系统软件流程

由于不能使用滤波器，系统在采集到加速度信号之后要通过软件修正方法去除加速度信号中的直流分量。去除直流分量的方法即为减去加速度信号的均值。

当DSP系统获得足够量的一次积分的速度值之后通过求其均值，处理得到趋势项，并在经一次积分得到的速度值上减去该值。根据系统的采样频率对一次积分得到的速度值进行分段，对每一小段数据点求均值得到速度值中的直流分量，用于对每一小段数据点进行处理。经过以上处理之后能够得到正确的速度值，通过A/D转换器AD5754输出。

4 试验验证

系统在实际的试验环境中进行了测试。试验设备包括信号采集仪PULSE，功率放大器BK2712，电荷放大器BK2626，电荷型加速度传感器BK4517，一块铝板和激振机BK4825。试验设备的连接如图2所示，铝板通过橡胶与地面相连。信号源输出信号经过功率放大器放大之后驱动激振机引起铝板的振动。加速度传感器检测平板的振动，输出信号经电荷放大器传输给DSP系统和信号采集仪PULSE。

图2 试验系统示意图

试验系统分别验证了对单频、多频和宽带加速度信号进行积分的试验效果。单频信号采用100 Hz的正弦波信号，多频信号采用含有120 Hz正弦波和200 Hz正弦波合成的信号，宽频信号采用带宽为200～400 Hz，频率间隔为3 Hz的正弦波信号构成。

图3为100 Hz的加速度信号及其积分所得的速度信号的时域波形，图4为相应的频谱图。从图中可以清楚地看出该加速度信号存在直流分量，积分程序有效地去除了加速度信号中的直流分量所产生的趋势项和直流偏移。通过与信号采集仪PULSE自带的积分功能积分得到的速度信号进行对比，发现积分所得速度信号的幅度值与真实的速度信号的幅度值一致，两者的相位大致保持一致，说明DSP系统积分得到的速度信号与实际的速度信号的相位基本一致。

(a)100 Hz的加速度信号

(b)积分所得速度信号图3 单频加速度及速度信号时域波形

图5为含有120 Hz和200 Hz两个频率成分的加速度信号及其积分所得的速度信号的时域波形。积分所得速度信号没有明显的波形畸变。图6为图5中加速度信号和速度信号的频谱图。通过与信号采集仪PULSE自带的积分功能积分得到的速度信号进行对比，发现DSP系统输出的速度信号中各频率成分的相位与实际速度信号的相位基本一致。

(a)加速度信号频谱图

(b)积分所得速度信号频谱图图4 单频加速度和速度信号频谱图

(a)120 Hz和200 Hz的加速度信号

(b)积分所得速度信号图5 多频加速度及速度信号时域波形

(a)加速度信号频谱图

(b)积分所得速度信号频谱图图6 多频加速度和速度信号幅频特性曲线

图7和图8分别为宽频加速度信号及其积分所得速度信号的时域波形，图9和图10分别为宽带加速度信号及其积分所得速度信号的频谱图。加速度信号的频率范围为200～400 Hz，频率间隔为3 Hz。通过Labshop软件对比两个信号的幅度信息和相位信息，可以验证该系统对于宽频信号的加速度积分同样正确。

5 结论

针对速度反馈振动主动控制系统，利用DSP控制系统和加速度传感器，在不使用滤波器的限制下，实现了加速度信号的时域积分。提出并论证了积分公式中速度初值的确定方法，随后提出了应用于实时控制系统的趋势项去除方法。去除趋势项的方法是在数值积分结果中减去积分结果的均值。该方法在DSP系统中进行了试验验证。结果表明：该系统对于单频信号、多频信号和宽频信号均能实现由加速度信号到速度信号的积分。积分结果有效地去除了加速度信号中的直流量及由此产生的趋势项，积分所得速度信号没有明显的波形畸变，所得速度信号的幅值与相位与实际速度信号的幅度与相位一致。

图7 宽带加速度信号时域波形

图8 宽带速度信号时域波形

图9 宽带加速度信号幅频特性曲线

图10 宽带速度信号幅频特性曲线

[1] 温广瑞，李杨，廖与禾，等．基于精确信息重构的故障转子系统振动加速度信号积分方法．机械工程学报，2013，49(8)：1-9．

[2] 耿保平，马震岳，王溢波，等．用于水电站振动信号的积分方法．振动、测试与振动，2011，31(5)：610-613．

[3] 代泽兵，黄金枝，郭自兴．加速度反馈磁流变阻尼器半主动控制．上海交通大学学报，2002，26(11)：1949-1955．

[4] TOM B，ARTHUR B．Active vibration control for underwater signature reduction of a navy ship．The 17th International Congress on Sound&Vibration，Cario，2010．

[5] 傅蕾，唐锡宽．状态监测系统分析软件精度提高的几点措施．清华大学学报，1998，38(8)：111-113．

[6] 陈隽，李杰．振动信号趋势项提取的几种方法及其比较．福州大学学报，2005，33(z1)：42-45．

[7] 胡小峰，叶庆泰，彭晓春．基于自适应滤波的悬臂梁振动速度反馈控制．机械强度，2004，26(3)：256-259．

[8] CHU S Y，SOONG T T，REINHORN A M．Active，Hybrid，and Semi-active Structural Control：A Design and Implementation Handbook．New York：Wiley，2005．

[9] 段智育，贾民平，许云飞，等．振动故障信号的软件积分研究与应用．机械制造与研究，2007，26(2)：79-81．

[10] 张永强，宋建江，屠良尧，等．软件数值积分误差原因分析及改进办法．机械强度，2006，28(3)：419-423.

Numerical Integration Method of Acceleration Signal in Active Vibration Control

WANG Zhen，SUN Yu-dong

(National Key Laboratory of Ship Vibration and Noise，China Ship Science Research Center，Wuxi 214082，China)

In the active vibration control system with velocity feedback control,the velocity signal is obtained by doing numerical integration of acceleration signal from acceleration sensor on a digital signal processing system.The velocity signal of the active vibration control system must be required with correct phase.To achieve correct velocity signal,an algorithm to acquire the correct initial phase value was proposed,constant value and the trend of error were eliminated without using digital or analog filter.The experiment shows that the algorithm is correct and it can provide correct velocity signal for the velocity feedback active vibration control system.

active vibration control;acceleration;numerical integration;velocity feedback

2013-11-09 收修改稿日期：2014-10-26

TH825

A

1002-1841(2015)02-0100-04

王震(1990—)，在读硕士研究生，主要从事振动噪声控制的研究。E-mail：wangzhen0130@126．com 孙玉东(1965—)，研究员，博士，主要从事船舶和水下航行体及机械与管路系统振动噪声研究。E-mail：wxsyd@tom．com