一类具有社团性质的二分网络

王剑凌 ，陈庆华

（1.福建江夏学院数理教研部，福建福州，350108；2.福建师范大学数学与计算机科学学院，福建福州， 350117）

复杂网络由节点和边组成，节点代表元素，边代表元素间的相互作用。复杂网络广泛应用于经济、工程、生物等社会的各个领域，比如，国与国之间的经济合作关系可以描述为世界贸易网，新陈代谢网能量化蛋白质之间的相互作用，人与人之间的相互关系构成人际关系网等。复杂网络在现实生活中发挥着举足轻重的作用，成为近年来学者研究的热点。

实证表明大多数实际网络具有一些共同的特征：网络规模庞大且结构复杂，演化过程具有随机性；网络是开放的，不断增加节点和边，实现网络增长；任意两个节点之间存在短路径，平均路径长度呈对数增长，且有明显的群聚趋势；网络具有幂律尾部，节点间度相关，存在极少数中枢点；随机去除有少数连边的节点，不会改变网络的拓扑结构。

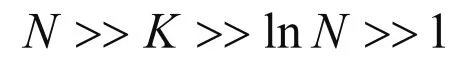
在此基础上，不少学者对模型进一步改进，更接近实际网络，如局部世界网络[3]、加权网络[4,5]等模型。Chen等考虑到节点的初始吸引力、重新布线等因素，对模型进行扩展，来研究无标度网络的生成机制[6]。Guillaume等提出很多实际网络都可视为二分网络，尤其是演员——电影、学生——课程、科研人员——文章等具有二分图结构的网络[7]。Xu等提出的社团网络，考虑到科学家合作关系不仅局限在同一领域，还有不同领域间的合作[8]。Furuya等根据医学院提供的处方记录，提出了DPN网络来描述药物之间的关系[9]。此外，对度分布的计算也有四种常见的方法：平均场方法[10]、率方程方法[11]、主方程方法[12]、马氏链方法[13,14]。本文基于Xu等的社团网络和Furuya等的DPN网络，提出一类具有社团性质的二分网络，来描述医生与药物之间的关系。

一、演化模型

初始时刻，⊥中有M个孤立的社团，每个社团有n1个孤立的点， 中有n2个孤立的点，在⊥与之间有m条边。

1.以概率p在⊥中随机选择一个区域加入新点，新点与 中n0个点连接的概率为

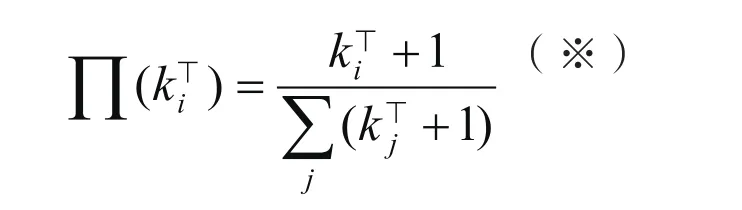
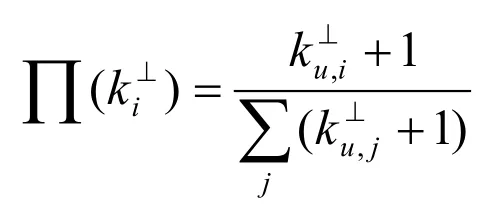
3.以概率r（=1-p-q）在⊥中随机选择一个区域中的一点，此点与中n0个点连接的概率同（※）

二、主要结论

定理2.1⊥的外部度分布具有幂律尾部，即

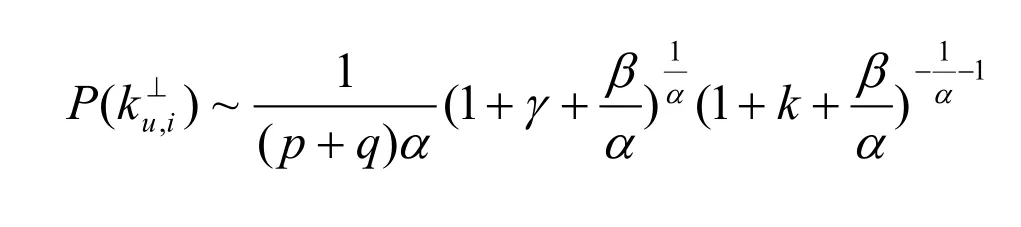
证明：在t时刻，的点数为，总点数为

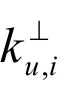
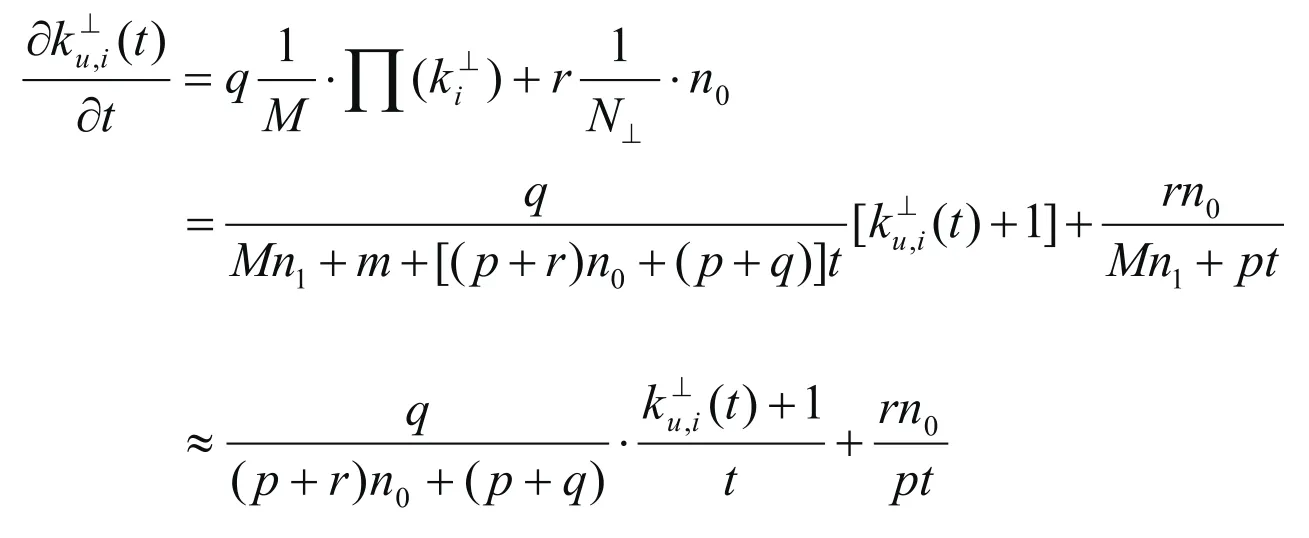
根据平均场方法的假设，点i进入系统的时间ti服从[0,t]上的均匀分布，则有

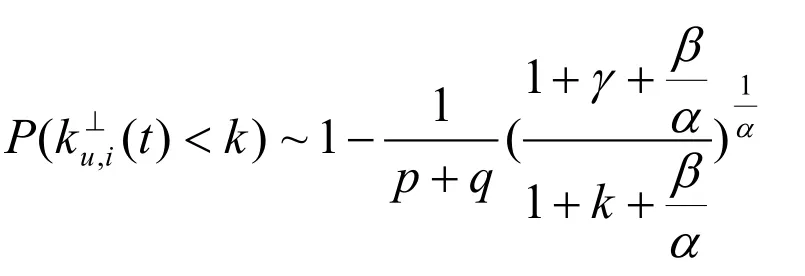
证明：在t时刻，的点数为，总点数为

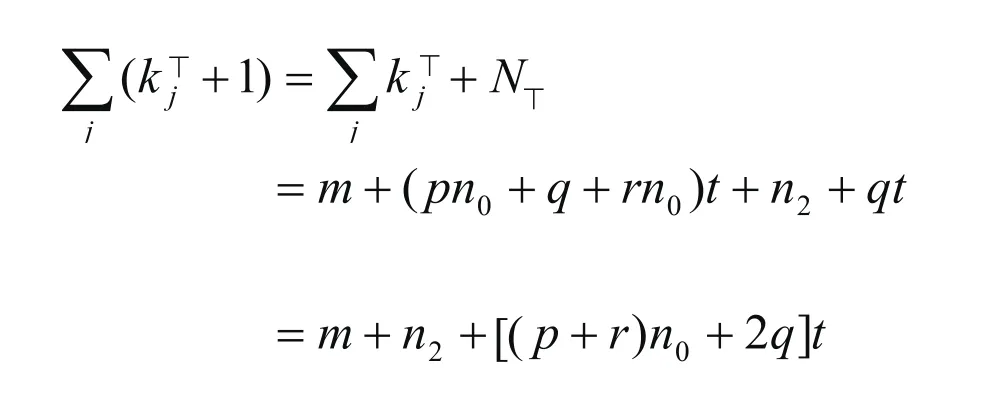
根据平均场方法的假设，点i进入系统的时间服从[0,t]上的均匀分布，则有

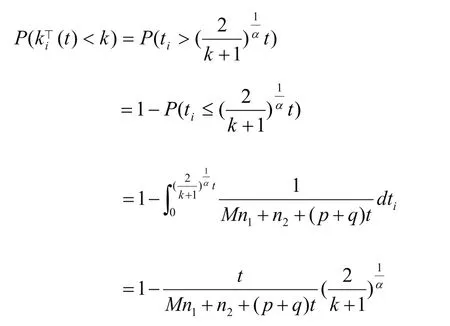
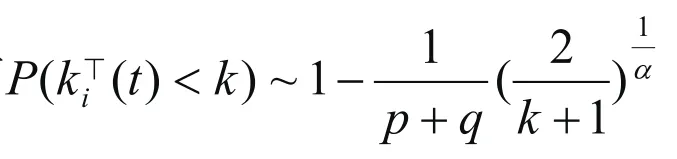
本文提出一类具有社团性质的二分网络，含有可调节的参数p,q,r，解析结果表明⊥和的外部度分布都具有幂律尾部。

[1]Watts D J,Strogatz S H.Collective dynamics of small-world networks[J].Nature,1998,393:440.

[2]Barabási A L,Albert R.Emergence of scaling in random networks[J].Science,1999,286:509-512.

[3]Li X,Chen G R.A local-world evolving network model[J].Physica A,2003,328:274-286.

[4]Yook S H,Jeong H,Barabási A L,Tu Y.Weighted evolving networks[J].Phys.Rev.Lett.,2001,86:5835-5838.

[5]Barrat A,Barthélemy M,Vespignani A.Modeling the evolution of weighted networks[J].Phys.Rev.E,2004,70:066149.

[6]Chen Q H,Shi D H.The modeling of scale free networks[J].Physica A,2004,335:240-248.

[7]Guillaume J L,Latapy M.Bipartite structure of all complex networks[J].Information Processing Letters,2004,90:215-221.

[8]Xu X J,Zhang X,Mendes J F F.Growing community networks with local events[J].Physica A,2009,388:1273-1278.

[9]Furuya S,Yakubo K.Scale-free property of local-world networks and their community structure[J].Physica A,2010,389:5878-5886.

[10]Barabási A L,Albert R,Jeong H.Mean-field theory for scale-free random networks[J].Physica A,1999,272:173-187.

[11]Krapivsky P L,Redner S,Leyvraz F.Connectivity of growing Random networks[J].Phys.Rev.Lett.,2000,85:4629-4632.

[12]Dorogovtsev S N,Mendes J F F,Samukhin A N.Structure of growing networks with preferential linking[J].Phys.Rev.Lett.,2000,85:4633-4636.

[13]Shi D H,Chen Q H.Markov chain-based numerical method for degree distributions of growing networks[J].Physical Review E,2005,71:036140.

[14]Chen Q H,Shi D H,Markov chains theory for scale free networks[J].Physica A,2006,360:121-133.