关于随机光滑点

赵世恩,赵 媛

(1.首都师范大学 初等教育学院,北京 100048;2.河北金融学院 基础部,河北 保定 071051)



关于随机光滑点

赵世恩1,赵 媛2

(1.首都师范大学 初等教育学院,北京 100048;2.河北金融学院 基础部,河北 保定 071051)

提出随机赋范模中随机光滑点的概念,利用随机赋范模与经典赋范空间的联系,给出了随机光滑点和经典光滑点的关系。最后,利用有限生成随机赋范模的代数结构,给出了几个随机光滑点的基本性质。这些结果将进一步丰富随机赋范模几何学已有的内容。

随机赋范模;随机共轭空间;随机光滑点;(ε,λ)-拓扑

0 引言

随机度量理论来源于概率度量空间理论[1],随机赋范模的概念是在随机度量理论的发展过程中提出来的,现在随机赋范模已成为随机度量理论的核心框架之一。当前采用的随机赋范模概念最终成型于文献[2]。在文献[1]中,随机度量空间中两点间的随机距离或向量的随机范数都采用非负随机变量来定义。文献[2]开始使用非负随机变量等价类来定义两点间的随机距离或向量的随机范数,这样虽然舍弃了一些概率论直观性,但从泛函分析的观点来看却带来了极大的方便。在随机赋范模上所赋予的一个重要拓扑是(ε,λ)-拓扑,从概率的角度来看是很自然的,但是这个拓扑不是局部凸的。因此，传统的共轭空间理论对于随机赋范模理论的发展是失效的。正因为如此,文献[2]开创性地提出了随机共轭空间的概念。随后,随机赋范模理论在随机共轭空间这一有利的工具下经历了快速的发展。

利用已有的关于随机赋范模理论的结果,对随机赋范模理论中的几何学做了进一步研究。首先，提出随机赋范模中随机光滑点的概念；其次,给出了随机光滑点和经典光滑点的关系；最后,给出关于随机光滑点的几个基本性质。

为了方便阅读,下面给出采用的记号:K表示实数域或复数域C;(Ω,,P)表示一个概率空间;L0(,K)表示(Ω,,P)上K-值-可测随机变量等价类所组成的代数;L0()=L0(,R)，L0()表示(Ω,,P)上广义-值-可测随机变量等价类所组成的集合。

1 预备知识

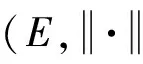
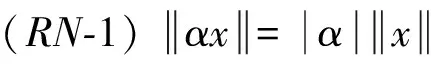
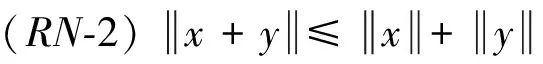
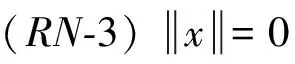
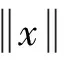
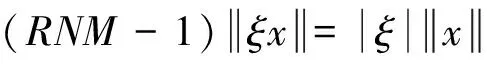
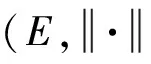
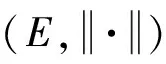
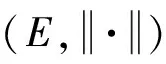
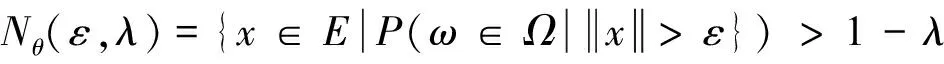
以及

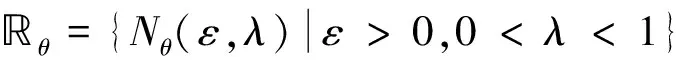
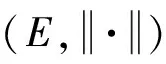
2 主要结果及其证明

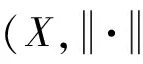
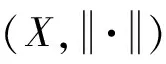
命题1[9]如果dimX=n,则AX依范数稠于X。

命题2[9-10]如果dimX=n,则存在AX中n个元素a1,a2,…,an,使得{fa1,fa2,…,fan}为X*的一组基。

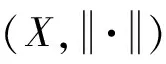
给出随机光滑点的概念以及主要结果的证明。

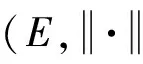
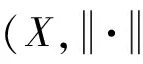
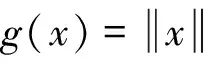
对于任意简单函数f:Ω→(n)′,因为{fx1,fx2,…,fxn}⊂(n)′为(n)′的一组基,容易证明f∈SpanL0{φ1,φ2,…,φn}。因此，在(ε,λ)-拓扑下SpanL0{φ1,φ2,…,φn}稠于L0(,(n)′)。又因为SpanL0{φ1,φ2,…,φn}在(ε,λ)-拓扑下是闭的,故有

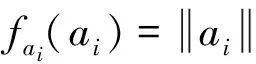
的元素。证毕。

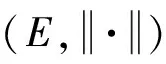
[1]SchweizerB,SklarA.ProbabilisticMetricSpaces[M].NewYork:Elsevier/North-Holland,1983.

[2]GuoTX.SomeBasicTheoriesofRandomNormedLinearSpacesandRandomInnerProductSpaces[J].ActaAnalFunctAppl,1999,1(2):160-184.

[3]GuoTX.RelationsBetweenSomeBasicResultsDerivedfromTwoKindsofTopologiesforARandomLocallyConvexModule[J].JFunctAnal,2010,258:3024-3047.

[4] Guo T X,Zeng X L.Random Strict Convexity and Random Uniform Convexity in Random Normed Modules[J].Nonlinear Anal Ser A:Theory,Methods and Applications,2010,73(5):1239-1263.

[5] Guo T X,Shi G.The Algebraic Structure of Finitely GeneratedL0(∑,K)-Modules and the Helly Theorem in Random Normed Modules[J].J Math Anal Appl,2011,381:833-842.

[7] Zhao S E,Guo T X.The Random Subreflexivity of Complete Random Normed Modules[J].Internat J Math,2012,23(3):1250047.

[8] 郭铁信,张霞.复完备随机内积模上的随机酉算子群的Stone表示定理[J].中国科学:数学,2012,42(3):181-202.

[9] Mazur S,Ulam S.Sur Les Transformations Isomatriques D’espaces Vectoriels Norms[J].Comptes Rendus Acad Sci Paris,1932,194:946-948.

[10] Figiel T.On Nonlinear Isometric Embeddings of Normed Linear Spaces[J].Serie des Sciences Math,Astr et Phys,1968,16(3):185-188.

国家自然科学基金项目(11401399);北京市自然科学基金项目(1144008)

赵世恩(1981-),男,河北张家口人,讲师,博士,研究方向为泛函分析.

2014-09-10

1672-6871(2015)04-0095-03

O177.92

A