MPU9250传感器的姿态检测与数据融合
刘春阳,徐军领,程洪涛,王东方,薛玉君
(河南科技大学 机电工程学院,河南 洛阳 471003)
MPU9250传感器的姿态检测与数据融合
刘春阳,徐军领,程洪涛,王东方,薛玉君
(河南科技大学 机电工程学院,河南 洛阳 471003)
设计了基于MPU9250多轴姿态传感器和MSP430F149单片机的姿态检测系统。利用传感器内部的陀螺仪、加速度计和电子罗盘,可以对3个轴的角速度、加速度、磁感应强度进行测量,进而解算成角度姿态。利用优化的卡尔曼滤波算法对解算的姿态角度进行了融合处理,融合后的数据有效地抑制了噪声,提高了角度姿态检测的准确性。设计的姿态检测系统每秒钟可以完成100次姿态检测与计算,具有体积小、响应快等特点,并应用于自平衡小车的姿态检测。
姿态检测;卡尔曼滤波;陀螺仪;加速度计;电子罗盘
0 引言
随着无人飞行器、虚拟现实装备、可穿戴装备等技术的发展,物体姿态检测成为获取姿态信息、实现精确运动控制的必要手段和前提条件。机械陀螺仪及光纤陀螺仪等高精度惯性导航传感器件价格昂贵[1]、体积较大,因此,在应用中大多利用微机电系统(MEMS)技术制造的陀螺仪、加速度计和电子罗盘等传感器进行姿态检测[2-3]。而单一传感器的姿态检测,容易因惯性器件的漂移和累计误差,导致测量精度的下降[4]。因此,通过多个传感器进行姿态检测,并借助数据融合算法提高姿态检测精度成为目前研究的热点[5]。
利用独立的陀螺仪、加速度计等多个传感器组合进行姿态检测,存在多个芯片占用空间大、姿态数据存在轴间误差、数据融合精度欠佳等不足[6-7]。因此,本文基于9轴姿态检测传感器MPU9250(内部集成陀螺仪、加速度计、电子罗盘),设计了以MSP430单片机为处理核心的姿态检测系统,由陀螺仪测量物体运动的角速度,进而解算成角度。利用加速度计和电子罗盘分别测量加速度和地磁场这两个不相关的三维矢量,作为物体姿态的观测矢量来校准陀螺仪的测量值。在数据融合方面,考虑到互补滤波在动态响应方面的不足,采用了卡尔曼滤波算法进行角度姿态估计,有效抑制了噪声,并提高了姿态角检测的准确性。
1 系统设计
设计的姿态检测系统以MSP430F149单片机为核心,通过姿态传感器MPU9250对运动姿态进行检测,以提供航向角、俯仰角和翻滚角等姿态信息。处理后的姿态角度信息可以显示在液晶屏上,也可以通过无线数据传输模块发送给远端的主机,并在上位机软件上完成数据的显示和运动曲线的绘制。此外,系统还设计了反馈控制接口,提供脉冲宽度调制(PWM)控制信号输出,可用于不同控制算法的验证研究。系统设计的框图如图1所示。
MPU9250为全球首例整合9轴运动姿态检测的数字传感器[8],消除了多传感器组合的轴间差问题,并减少了传感器的体积,降低了系统的功耗。MPU9250内部集成有3轴陀螺仪、3轴加速度计、3轴电子罗盘,输出信号都是16位的数字量;可以通过集成电路总线(IIC)接口和单片机进行数据交互,传输速率可达400 kHz/s。陀螺仪的角速度测量范围最高达±2 000 (°)/s,具有良好的动态响应特性。

图1 姿态检测系统设计框图
加速度计的测量范围最大为±16g(g为重力加速度),静态测量精度高。电子罗盘采用高灵敏度霍尔型传感器进行数据采集,磁感应强度测量范围为±4 800 μT,可用于对偏航角的辅助测量。
2 数据处理
2.1 角度的计算
传感器传输回来的数据分别代表3个轴测量的角速度、加速度和磁感应强度,需要解算成姿态角度信息,主要是俯仰角ρ(X轴与地面的角度)、翻滚角φ(Y轴与地面的角度)和航向角α(绕Z轴旋转的角度)。
陀螺仪测量的是旋转的角速度,通过积分就可以得到对应的角度值[7],计算公式如下:
θk=(ωk-ωbias_k)dt+θk-1,
(1)
其中:θk为当前时刻的角度值;θk-1为前一时刻的角度值;ωk为陀螺仪测量当前时刻的角速度;ωbias_k为当前时刻角速度的偏移量;dt为积分时间,即角度计算的采样周期。
加速度计测量3个轴的加速度分量,可利用三角函数关系解算角度姿态[9]:
(2)
其中:Ax、Ay、Az分别是X、Y、Z这3个轴的加速度分量;γ为Z轴与重力加速度的夹角;ρ为俯仰角;φ为翻滚角。
电子罗盘测量的是3个轴的磁感应强度,由于X、Y两轴的磁感应强度合成后总指向地磁北极,因此,可通过测量敏感轴与地磁北极的夹角来实现航向角的检测。电子罗盘在水平位置且无外加磁场干扰时,航向角可通过如下三角函数关系计算:

(3)
其中,Hx和Hy分别为X轴和Y轴输出的磁感应强度数据。
当电子罗盘不在水平位置的时候,可通过倾斜补偿方法,减小航向角检测的误差[10]。倾斜补偿公式为:
(4)

2.2 卡尔曼滤波
在角度姿态融合中,互补滤波和卡尔曼滤波是常见的处理算法,而从滤波效果来看,互补滤波的动态融合精度低,响应速度没有卡尔曼滤波快[11]。因此,系统设计中采用了卡尔曼滤波算法对角度姿态数据进行融合处理。
卡尔曼滤波是以系统的观测量作为滤波器的输入量,以系统状态量的估计值作为滤波器的输出量,利用系统噪声和观测噪声的统计特性进行最优估计的数据处理方法[12]。假设系统的状态方程和测量方差可用如下线性公式描述[13]:
(5)
其中:xk为状态向量;yk为观测向量;A为从k-1时刻到k时刻的状态转移矩阵;Uk为系统输入控制向量;B为输入控制向量的增益矩阵;H为状态量到观测量的增益矩阵;wk为输入噪声;vk为观测噪声。假定输入噪声和观测噪声都是服从正态分布,输入噪声的协方差为Q,观测噪声的协方差为R,则卡尔曼滤波递推公式可概括为5个核心公式[13]:
状态量的预估计,
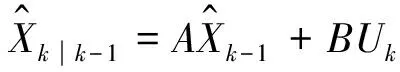
(6)
误差协方差预估计,
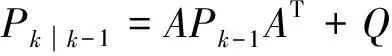
(7)
卡尔曼增益更新,
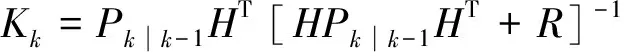
(8)
现状态估计值更新,
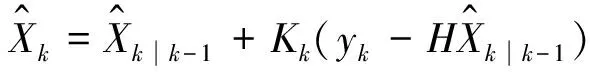
(9)
误差协方差更新,

(10)

对于姿态检测系统,陀螺仪的角度状态可用式(1)描述,加速度计和电子罗盘测量的对应角度值可作为观测反馈值。为了抑制陀螺仪的漂移,系统还需要对偏移量进行估计处理,所以系统的状态方程可用如下公式描述:
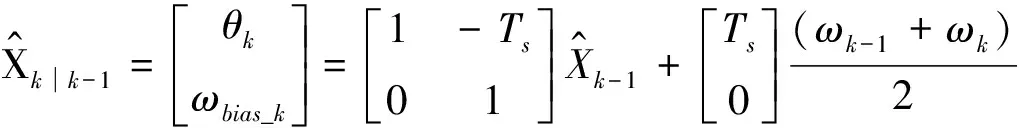
(11)
其中:Ts为采样周期;ωk和ωk-1分别为陀螺仪测量k时刻以及k-1时刻的角速度。
R和Q的取值会影响滤波的效果和响应速度:R取值越小,响应越快,收敛越迅速;Q取值越小,抑制噪声的能力越强,但收敛和响应变慢。在系统的软件处理程序中,优化后的卡尔曼滤波的各项系数设定初始值如下:
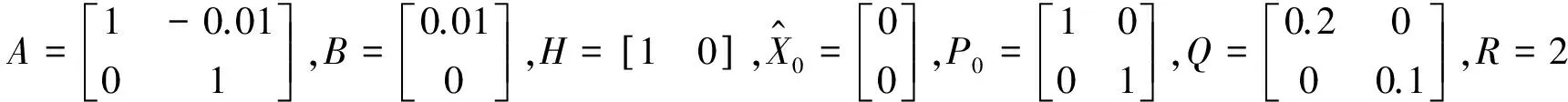
3 实验与分析
系统完成角度姿态数据的采集和处理后,将角度信息通过无线传输模块传输给主机,主机再传输给上位机,并利用自主设计的上位机软件进行显示和运动曲线绘制,便于对角度姿态的变化进行分析。
图2是对已知角度姿态的静态测量数据。利用实验室的角度分度装置,设置了0°和35°两个测试位置,利用系统采集传感器的数据,将卡尔曼滤波后所得数据与陀螺仪、加速度计分别测量的角度数据进行了比较。从图2a中可以看出:在0°位置,加速度计存在较明显的噪声,最大的噪声达到了±0.9°;而陀螺仪则存在较明显的漂移,随着时间的延长,测量角度累计误差增大;卡尔曼滤波后得到的俯仰角,在一定程度上抑制了加速度计的噪声,角度误差降低到±0.5°范围内,并且对陀螺仪的漂移也进行了修正,提高了角度姿态检测的准确性。图2b是在35°位置静止时俯仰角的测量曲线,卡尔曼滤波同样起到了很好的修正作用,降低了测量误差。测量结果验证了系统的测量姿态角度的可行性和准确性。
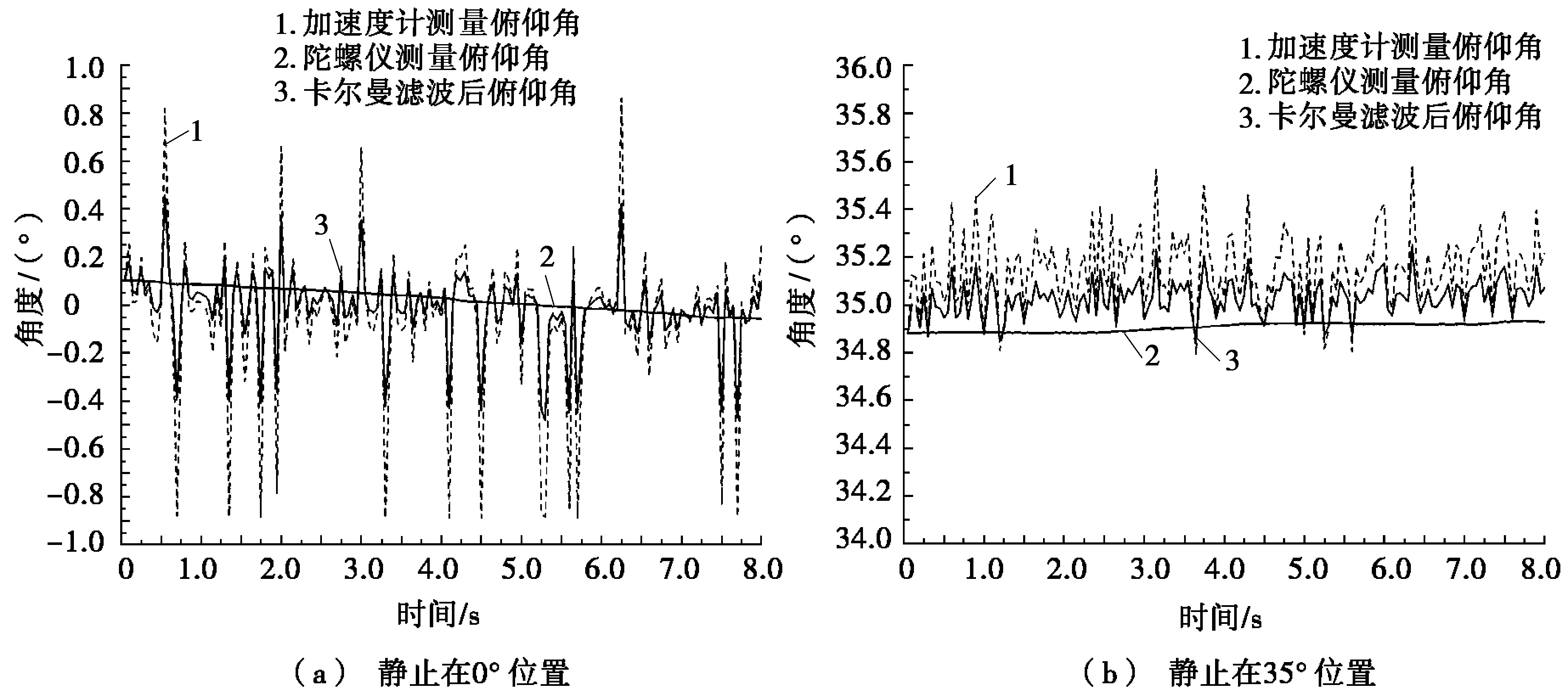
图2 静止状态下俯仰角的测量结果

图3 运动状态下卡尔曼滤波前后俯仰角检测结果比较
图3为运动状态下系统测量的俯仰角。随着传感器姿态的调整,陀螺仪和加速度计都及时跟踪了角度变化。从图3的局部放大数据可以看出:陀螺仪的动态响应更好;加速度计的噪声比较明显,并存在一定滞后现象;卡尔曼滤波对数据进行了有效的融合处理,满足了系统对姿态检测的要求。
通过实验分析,设计的姿态检测系统工作良好,经过卡尔曼滤波算法融合的数据能及时跟踪系统姿态的变化,并有效抑制了加速度计的噪声,降低了陀螺仪的漂移,提高了姿态检测的准确度。
4 结论
利用姿态检测传感器MPU9250和MSP430单片机搭建的姿态检测系统,实现了姿态角度检测的功能;并通过卡尔曼滤波算法对陀螺仪、加速度计、电子罗盘解算的角度信息进行了融合处理,提高了姿态角度检测的准确性。该系统具有响应快、接口丰富、实时性好等特点,并可应用于机器人、无人机姿态检测、惯性导航、虚拟现实装备等领域。
[1] 王巍.惯性技术研究现状及发展趋势[J].自动化学报,2013,39(6):723-729.
[2] 秦勇,臧希喆,王晓宇,等.基于MEMS惯性传感器的机器人姿态监测系统的研究[J].传感技术学报,2007,20(2):298-301.
[3] 夏圣,许勇.基于MEMS组合模块的姿态检测系统设计[J].单片机与嵌入式系统应用,2011(4):52-55.
[4] 梁建宏,田伟程,王田苗.基于ARM与低成本MEMS的AHRS设计[J].单片机与嵌入式系统应用,2012(5):1-4.
[5] 毕盛,闵华清,李淳,等.姿态传感器采集测试系统的设计与实现[J].计算机测量与控制,2011,19(7):1562-1564.
[6]FosterCC,ElkaimGH,SantaCUC.ExtensionofaTwo-StepCalibrationMethodologytoIncludeNonorthogonalSensorAxes[J].IEEETransactionsonAerospaceandEledtronicSystems,2008,44(3):1070-1078.
[7] 李伟,何鹏举,高社生.多传感器加权信息融合算法研究[J].西北工业大学学报,2010,28(5):674-678.
[8] MPU9250数据手册[EB/OL].[2015-01-23].http://www.invensense.com/mems/gyro/mpu9250.html.
[9] Kimberly T.Tilt Sensing Using Linear Accelerometers[J].Freescale Semiconductor Application Note,2007,6:1-7.
[10] 邵婷婷,马建仓,胡士峰,等.电子罗盘的倾斜与罗差补偿算法研究[J].传感技术学报,2007,20(6):1335-1337.
[11] 郜园园,阮晓钢,宋洪军,等.两轮自平衡机器人惯性传感器滤波问题的研究[J].传感技术学报,2010,23(5):696-700.
[12] 付梦印,邓志红,闫莉萍.Kalman滤波理论及其在导航系统中的应用[M].北京:科学出版社,2010:17-18.
[13] 杨凌霄,李晓阳.基于卡尔曼滤波的两轮自平衡车姿态检测方法[J].计算机仿真,2014,3(6):406-409.
河南省基础与前沿技术研究基金项目(142300413217);河南省教育厅基金项目(14B460028);河南科技大学青年基金项目(2012QN0025)
刘春阳(1982-),男,满族,河北承德人,讲师,博士,主要研究方向为精密测试技术.
2014-12-01
1672-6871(2015)04-0014-04
TP216
A

