独塔自锚式悬索桥车桥耦合振动响应研究

李洪泉,赵明帅,陈彦江

(北京工业大学 建筑工程学院，北京100124)



独塔自锚式悬索桥车桥耦合振动响应研究

李洪泉,赵明帅,陈彦江

(北京工业大学 建筑工程学院，北京100124)

选用基于ANSYS和MATLAB的分离迭代算法，将车辆和桥梁看作两个分离的子系统，分别采用虚功原理和有限元法推导了两者的振动方程；以车桥接触点位移协调关系和力的平衡关系为联系，研究了独塔自锚式悬索桥在不同的路面不平整度、车速、桥梁阻尼下的动力响应问题。研究表明：路面不平度对桥梁动力响应影响很大，冲击系数随车速呈波形变化，增大桥梁结构阻尼比对降低结构的动力响应影响较小；现有规范冲击系数取值对该类桥梁结构设计偏于不安全，建议规范独立地给出悬索桥冲击系数的规定，并考虑路面等级、车速的影响。

桥梁工程；自锚式悬索桥；车桥耦合；分离迭代算法；冲击系数

0 引 言

当汽车以一定的速度通过桥梁时，由于车辆自身各旋转部分的作用，以及速度、桥面不平顺等因素的影响，会引起车体悬架部分的振动，并通过具有一定弹性与阻尼作用的轮胎传递给桥面，引起桥梁的振动，而桥梁的振动又反过来影响车辆的振动，这种车桥之间振动状态相互影响、相互关联的问题就是车桥耦合振动问题[1]。

随着现代车桥耦合计算理论的繁荣发展，对桥梁模型的研究已从过去简单形式的桥梁向各种复杂形式进行了开展，如双层公路钢桁架梁桥、曲线梁桥、大跨连续体系梁桥、钢管混凝土拱桥、斜拉桥及悬索桥。自锚式悬索桥作为一种新型的桥梁结构形式，其不需专门设计锚碇、对地形和地质条件适应能力强以及结构造型美观等突出优点，使其在一些中小跨径的城市桥梁方案比选中很具竞争力，越来越受到工程界的青睐，然而有关该桥型在移动车辆荷载作用下的动力响应问题的研究相对较少。考虑到该桥型具有不同于地锚式悬索桥的结构形式和受力特征，其振动响应有一定的特殊性，因此，研究其在移动荷载作用下的动力响应问题就具有重要的理论价值和工程实际意义。

1 车桥耦合振动分析原理

目前基于时域法的车桥耦合振动分析方法主要有以下两种：①将车桥系统以接触点为界，分为车、桥两个子系统，以接触点处的位移协调条件和力的平衡关系为耦合关系，采用迭代法求解；②将车辆与桥梁的所有自由度联立在一起，建立统一的方程组采用直接积分法同步求解[2]。前者是一种近似的算法，仅在较小的积分时间步长上具有算法上的准确性，但其机理明确，思路清晰，可处理非线性问题，适用于分析复杂桥梁结构和精细车辆模型，因此，笔者采用该法进行求解。

1.1 车辆模型及其振动方程

目前对车辆的模拟主要有整车模型、半车模型、单轮车梁模型三种。半车模型认为车辆左右两侧的车轮以高度相关的方式运动，故把车辆简化为半车模型。同时，对于大跨度桥梁而言，车辆系统自身的动力特性对桥梁动力响应影响较小[3]，为计算简便，笔者拟采用平面双轴半车模型，如图1。

图1 双轴半车模型

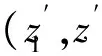
(1)

根据虚功原理，可推得车辆系统振动方程为：

(2)

若考虑桥面的不平度项，则fvi变为：

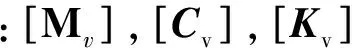
1.2 桥梁结构振动方程

自锚式悬索桥的有限元模型采用鱼骨式模型，桥梁结构的振动方程[4]可写成：

(3)

假定车轮与桥面始终保持接触，利用车桥接触点处的力和位移的协调条件[5]，可得桥梁结构在前、后车轮处受到的激励为：

(4)

1.3 桥面不平度的模拟

图2 路面不平度曲线

1.4 分析流程

笔者是通过MATLAB和ANSYS两个软件相互迭代实现车桥耦合分析流程的。将车桥耦合体系分成两个子体系——车辆振动方程和桥梁振动方程，基于MATLAB强大的数值计算功能求解车辆运动方程，利用ANSYS完全法瞬态动力分析求解桥梁运动方程，以力和位移的协调条件作为两者之间的耦合。具体分析流程如下：

1)首先对桥梁进行静力分析，同时计入大变形效应、应力刚化效应，以获得桥梁的初始平衡状态；

2)将车辆的重力荷载施加在桥梁上，作为对桥梁的初始迭代值，并利用ANSYS的完全法瞬态动力分析功能求解桥梁运动方程，以获得车桥接触点处(桥梁)的时间-位移、时间-速度向量，保存为外部文件；

3)在MATLAB软件中读入第2)步车桥接触点处(桥梁)的位移、速度向量，考虑不平度影响，计算车辆的外部激励向量；

4)根据第3)步中的车辆外部激励向量，考虑车辆的初始振动情况(假设车辆的初始振动由上桥前200 m获得)，利用Newmark-β法求解车辆振动方程，提取出车辆的时间-位移向量和时间-速度向量；

5)在MATLAB软件中根据式(4)计算桥梁受到的激励向量，保存为外部文件；

6)将前后两次得到的桥梁激励向量进行收敛分析，若不满足收敛条件，则代替第1)步中的重力荷载向量，即重复2)～5)步，直到满足收敛条件为止；

7)将满足收敛条件后的车辆对桥梁激励向量再次读入ANSYS内存中，求解并获得桥梁最终的动力响应。

1.5 算例验证

为验证笔者方法及自编程序的正确性，选取了文献[7]中的简支梁作为算例。车辆模型为双轴四自由度半车模型，如图1，参数如表1。简支梁的技术参数为：计算跨径40 m，单位长度质量1.2×104kg/m，抗弯刚度1.275×1011N·m2，泊松比0.2。不考虑桥梁阻尼与路面不平度的影响。

表1 车辆模型技术参数

分析在速度10，20，30，40，50 m/s下，以桥梁跨中挠度时程曲线为对比依据，计算结果列于图3。笔者计算结果与文献[7]给出的结果在不同速度下位移幅值及变化规律基本一致，说明了笔者提出的方法及程序的正确性，可以应用其进行车桥耦合振动方面的研究。

图3 笔者计算结果

2 自锚式悬索桥概况及有限元模型

2.1 工程概况

笔者以某独塔自锚式悬索桥为研究对象，其桥跨布置为35 m+135 m+165 m+35 m，双向6车道，主塔为高126.5 m的预应力混凝土结构，呈“种子”型，桥型布置见图4。加劲梁采用扁平钢箱梁，见图5。全桥共设两根主缆，横向间距为29.5 m，每根主缆由33股127丝Φ5.1 mm的镀锌高强钢丝组成，公称抗拉强度为1 670 MPa，成桥后设计主跨垂跨比为1∶12.5。主跨顺桥向(从左往右)共布设27对吊索，标准间距为9.0 m，主塔两侧的吊索距塔中心线11 m，单根吊索采用85丝Φ7 mm平行镀锌高强钢丝，端部1、27号吊索采用151丝Φ7 mm平行镀锌高强钢丝，两端均采用冷铸锚锚固体系。设计荷载标准为公路-Ⅰ级，人群荷载取4.5 kN/m2，设计时速为100 km/h。

图4 桥型布置图(单位：cm)

图5 主梁一般构造图(单位：cm)

2.2 有限元模型

根据相关设计文件，将二期恒载等效为梁体的线密度，运用大型通用软件ANSYS建立起全桥成桥状态的有限元模型，如图6。其中主缆及吊索采用只受拉的LINK10单元模拟，主梁、主塔采用BEAM44单元模拟，采用鱼骨式模型。模型中的约束条件为：桥塔与地基固结，塔顶与主缆耦合，主缆锚固点与主梁耦合，主梁在桥塔横梁处横向、竖向以及绕顺桥向、竖向转角自由度耦合，混凝土锚跨梁段在桥墩处横向、竖向以及绕顺桥向、竖向转角自由度耦合。对桥梁进行了模态分析，采用LANB法求得了其前100阶振型。表2列出了前10阶频率及其振型。

图6 全桥有限元模型

表2 前10阶振动频率及振型

(续表2)

3 自锚式悬索桥车桥耦合参数分析

3.1 动力冲击系数

根据2004年《公路桥涵设计通用规范》，汽车荷载的冲击系数可表示为：

(5)

式中:Yd,max、Yj,max分别为汽车过桥时桥梁结构的最大动力效应(位移或内力)和最大静力效应。

3.2 桥面不平度的影响

文献[8-9]指出，桥面不平度对车桥耦合有很大的影响，笔者选取了4种不平度等级，分别为理想、B级、C级、D级。选取了4种截面：长跨跨中的竖向位移(1号截面)、短跨跨中的竖向位移(2号截面)、长跨跨中的弯矩(3号截面)、长跨跨中的吊杆力(4号截面)。车辆参数见表1，车速为60 km/h，桥梁结构阻尼比为1.89%。限于篇幅仅列出1号截面的动力响应如图7，4种截面的动力冲击系数见图8。

图7 不同路面等级下1号截面动力响应

图8 冲击系数与不平度等级的关系

由图7、图8可以看出：①总体上讲，随着桥面状况的恶化，汽车对桥梁结构的冲击作用变大，桥梁结构的动力响应变大，波动性更加剧烈；且不平度等级越低，其冲击系数增大越快，说明路面不平度对车桥耦合有很大的影响，因此，无论对于新桥或旧桥，一定要重视路面质量的建设和管理；②在理想路面状态下，各关键截面得到的动力效应增加值较为平缓，变化不大，基本与静力影响线相当，是因为车辆行驶时受到的激励主要来自桥梁自身的下挠程度，数值较小，因此引起的车辆振动及其对桥梁的作用力亦较小。

3.3 车速的影响

车速从两个方面影响车桥耦合系统：一方面车速越大，车辆的动能越大，车桥耦合响应变大；另一方面车速越大，车桥相互作用的时间变短，车桥耦合响应变小[6]。考虑到以上两个因素作用是相反的，其振动响应随车速影响变化规律比较复杂。笔者选取了10 m/s(36 km/h)，15 m/s(54 km/h)，20 m/s(72 km/h)，25 m/s(90 km/h)，30 m/s(108 km/h)五个常见的行驶速度，不平度等级选为B级，桥梁结构阻尼比为1.89%，仅列出1号截面的动力响应如图9，4种截面的动力冲击系数如图10。

图9 不同速度下1号截面动力响应

图10 冲击系数与车辆行驶速度的关系

由图9、图10可以看出：在选取的车速范围内，随着车速的增大，不同截面位置所得到的冲击系数规律不尽相同：1号截面在15，30 m/s时出现了两个峰值，2号截面则在10，25 m/s时出现了峰值，3号截面是在15，30 m/s处出现了峰值，4号截面是在25 m/s处出现了峰值。

这是由于车速的变化，导致了车辆对桥梁激振力的频率也在发生变化，当其与桥梁某截面的振动频率一致时，便产生共振，使得该截面的冲击效应达到较大。对1、3号截面(长跨跨中位移、弯矩)而言，车速为30 m/s时激振力的频率为0.943 Hz，较接近主梁竖弯频率0.962 Hz，对应振型为竖向对称弯曲，使得冲击效应较为明显。

3.4 桥梁结构阻尼的影响

阻尼特性是结构的重要动力特性，反映了结构对外界输入能量耗散能力的大小，已有研究表明，结构的阻尼对车桥耦合振动有一定的影响。鉴于目前钢结构的实测阻尼比在0.030左右，选取了4组不同的阻尼比0，0.015，0.030，0.045进行分析，采用目前广泛应用的Rayleigh阻尼模型，不平度等级取为B级，车速取60 km/h，1号截面的动力响应如图11，4种截面的动力冲击系数见图12。

图11 不同阻尼比下1号截面动力响应

图12 冲击系数随桥梁结构阻尼比的关系

由图11、图12可以看出：随着阻尼比的增大，4个截面的冲击系数都表现出相同变化趋势，即它们均随着结构阻尼比的增大而减小，这是由于高阻尼体系使结构的耗能能力加强，在一定程度上可以降低结构的动力响应；但不同截面的变化范围不相同，在笔者考虑的阻尼比范围内，4号截面的变化范围最大，首先从阻尼比为0时的1.230变化到阻尼比为0.015时的1.094，变化较为剧烈，然后又较为平缓地变化到阻尼比为0.045时的1.065，说明较小的阻尼比对4号截面的动力响应影响较大，增大阻尼比并不能大幅降低其动力响应；其它3个截面的变化则较为平缓，从其动力响应图上可以看出，增大阻尼比对降低动力响应有一定影响，但影响较小。

3.5 规范冲击系数合理取值的初步探讨

根据现行的《公路桥涵设计通用规范》，该桥的冲击系数取值为1.05，而笔者在B级路面下得到的结果大部分超出了1.05，表明规范中冲击系数的取值对该类桥梁结构设计偏于不安全。究其原因，一是悬索桥属于柔性体系，其基频大多小于1.5 Hz，故按规范为1.05；二是冲击系数与路面等级、车速等有着本质的关系，而规范中只考虑了桥梁基频这一因素，显然是不合理的。

因此，建议规范将悬索桥这一桥型分离出来，独立地给出悬索桥冲击系数的规定，并考虑路面等级、车速的影响。

4 结 论

笔者基于ANSYS和MATLAB的分离迭代算法进行了自锚式悬索桥的车桥耦合振动响应研究，得到了如下的结论：

1)路面等级对振动响应影响很大，且路面等级越低，冲击系数值增大越快。

2)桥梁不同截面冲击系数随车速的变化规律不尽相同，基本呈波形变化。

3)增大桥梁结构阻尼对降低结构的动力响应影响较小。

4)现有规范冲击系数取值对桥梁结构设计偏于不安全，建议规范独立地给出悬索桥冲击系数的规定，并考虑路面等级、车速的影响。

5)长跨跨中位移的冲击系数均大于长跨跨中弯矩冲击系数，故设计时可以采用位移冲击系数为基准以偏于安全。

[1] 王永平,陈彦江,傅金科.单车荷载下简支梁桥的动力特性和响应的试验研究[J].土木工程学报,1995,28(5):39-46. Wang Yongping,Chen Yanjiang,Fu Jinke.Experimental and theoretical analysis of dynamic characteristics and response of highway bridge under single moving vehicle[J].China Civil Engineering Journal,1995,28(5):39-46.

[2] 谢秉敏,向中富,王小松,等.基于ANSYS的车桥耦合动力分析[J].重庆交通大学学报:自然科学版,2012,31(5):935-938. Xie Bingmin,Xiang Zhongfu,Wang Xiaosong,et al.Dynamic analysis method of vehicle-bridge coupling based on ANSYS[J].Journal of Chongqing Jiaotong University:Natural Science,2012,31(5):935-938.

[3] Tommy H T C,Guo L,Li Z X.Finite element modelling for fatigue stress analysis of large suspension bridges[J].Journal of Sound and Vibration,2003,261(3):443-464.

[4] 刘永建,刘世忠,米静,等.双层公路钢桁梁桥车桥耦合振动[J].交通运输工程学报,2012,12(6):20-28. Liu Yongjian,Liu Shizhong,Mi Jing,et al.Vehicle-bridge coupled vibration of highway double-deck steel truss bridge[J].Journal of Traffic and Transportation Engineering,2012,12(6):20-28.

[5] 童忠选.大跨度斜拉桥车桥耦合振动的动力性能分析[D].长沙:长沙理工大学,2013. Tong Zhongxuan.Dynamic Performance Analysis of Long-Span Cable-Stayed Bridge Coupled Vibration[D].Changsha:Changsha University of Science and Technology,2013.

[6] Hwang E S,Nowak A S.Simulation of dynamic load for bridges[J].Journal of Structural Engineering,ASCE,1991,117(5):1413-1434.

[7] 桂水荣,陈水生,许士强.移动荷载下简支梁桥3种车桥耦合模型研究[J].华东交通大学学报,2007,24(1):35-39. Gui Shuirong,Chen Shuisheng,Xu Shiqiang.Comparison of three models for vehicle bridge coupled vibration of simple beam bridge subjected to moving load[J].Journal of East China Jiaotong University,2007,24(1):35-39.

[8] 王达,韩万水,黄平明,等.桥面平整度对大跨度悬索桥车桥耦合振动的影响[J].长安大学学报:自然科学版,2009,29(4):53-58. Wang Da,Han Wanshui,Huang Pingming,et al.Influence of bridge surface roughness on vehicle-bridge coupled vibration of long-span suspension bridge[J].Journal of Chang’an University:Natural Science Edition,2009,29(4):53-58.

[9] 易晋生,顾安邦,王小松,等.车桥耦合振动理论在桥面不平度研究中的应用[J].重庆交通大学学报:自然科学版,2013,32(4):560-563. Yi Jinsheng,Gu Anbang,Wang Xiaosong,et al.Application of vehicle-bridge coupling vibrations theory in the study of bridge surface roughness[J].Journal of Chongqing Jiaotong University:Natural Science,2013,32(4):560-563.

Research on Vehicle-Bridge Coupling Vibration of Self-Anchored Suspension Bridge with Single-Tower

Li Hongquan, Zhao Mingshuai, Chen Yanjiang

(College of Architecture and Civil Engineering, Beijing University of Technology, Beijing 100124, China)

Based on separated iterative algorithm of ANSYS and MATLAB, the motion equations of the vehicle and the bridge which were regarded as two separated subsystems were derived by virtual work principle and finite element method respectively. The displacement coordination condition and force balance relation at contact point were taken into consideration, in order to study the responses of self-anchored suspension bridge with single-tower under various road roughness, vehicle speed and bridge damping. Results indicate grade of road roughness has great influence on dynamic response of bridge. The impact factor behaves wavelike at different speeds. With increase of damping, the response tends to diminish in little degree. In addition, impact factor in current specification tends to be unsafe for structure design of this type of bridge. It is advised that the impact factor of suspension bridge should be regulated separately, considering the effects of road roughness and speed.

bridge engineering; self-anchored suspension bridge; vehicle-bridge coupling; separated iterative algorithm; impact factor

2014-05-09；

2014-09-12

李洪泉(1956—)，男，黑龙江哈尔滨人，教授，博士，主要从事工程抗震减灾方面的研究。E-mail：lhqqq@bjut.edu.cn

10.3969/j.issn.1674-0696.2015.03.01

U441+.3

A

1674-0696(2015)03-001-06