矩形带肋钢板-混凝土复合梁裂缝宽度计算方法
王晓东,魏文龙,唐 亮
(1.武汉理工大学,湖北 武汉 430070;2.西藏自治区交通勘察设计研究院,西藏 拉萨 850001;3.重庆交通大学 土木建筑学院,重庆 400074)
矩形带肋钢板-混凝土复合梁裂缝宽度计算方法
王晓东1,2,魏文龙3,唐 亮3
(1.武汉理工大学,湖北 武汉 430070;2.西藏自治区交通勘察设计研究院,西藏 拉萨 850001;3.重庆交通大学 土木建筑学院,重庆 400074)
参照普通钢筋混凝土裂缝计算的黏结-滑移理论,推导了适用于矩形带肋钢板-混凝土复合梁(Ribbed Steel-Concrete Composite Beam,RSCC梁)的裂缝间距公式;在理论上解释了在同等配筋率下RSCC梁的裂缝间距较普通钢筋混凝土梁小的试验现象;在加劲肋钢板顶部应变计算公式的基础上,参照普通钢筋混凝土裂缝计算的综合理论给出了RSCC梁的最大裂缝宽度计算公式;通过试验数据拟合得到了相关参数。
桥梁工程;裂缝宽度;开裂弯矩;带肋钢板-混凝土复合梁;增强机制
0 引 言
裂缝的出现会降低钢筋混凝土结构的刚度、耐久性,使结构挠度增加,限制了结构的使用范围。预应力钢筋混凝土结构较好地解决了大跨径、长区段的混凝土结构的开裂难题,但对连续梁和无铰拱拱脚等结构的负弯矩区段的混凝土结构局部区域的拉应力峰值过大,及沿构件长度方向拉应力迅速减小,通过较短区段即变化为压应力的问题至今没有较好的解决办法。目前常采用的方法有:增加结构构件的截面尺寸、在局部拉应力峰值区段施加预应力、拉应力较大区域粘贴钢板或FRP,这些方法在一定程度上解决了局部区域拉应力峰值过大所引起的混凝土结构开裂问题,但缺点和局限性也较为明显[1]。
自20世纪30年代以来,各国学者针对钢筋混凝土构件提出了各种不同的裂缝计算理论以及包括各种不同变量的、不同形式的裂缝计算公式。由于影响裂缝的因素较多,各国关于计算裂缝的公式也有着比较大的差别。从目前使用的裂缝计算理论来看,主要有粘结-滑移理论、无滑移理论及综合理论等3种裂缝计算理论。1936年R. Saligar[2]根据钢筋混凝土轴心受拉杆件的试验提出了粘结-滑移理论,一直被认为是经典的裂缝计算理论。20世纪60年代由J.F.Borges,等[3],G.D.Base[4]首先提出了无滑移理论,继而B.B.Broms[5-6]提出了基于综合理论的裂缝平均间距的公式,我国GB 50010—2010《混凝土结构设计规范》采用的是综合理论。
为达到较大地提高混凝土结构局部拉应力控制区域抗裂性能的目的,笔者依照纤维复合材料阻滞横向裂纹的基本原理,结合开孔钢板连接件的基本构造,提出了带肋钢板-混凝土受弯构件横截面,如图1,在构件的局部拉应力控制侧设置带肋钢板,在加劲肋板上按一定间距开孔,构件箍筋穿过加劲肋板上的开孔。带肋钢板、纵向钢筋和箍筋等形成带肋的强化钢板-钢筋整体骨架,再浇注混凝土即形成带肋钢板-混凝土复合结构。笔者主要探讨这种复合结构的裂缝宽度计算方法。
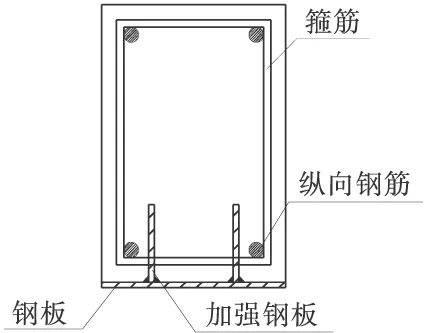
图1 带肋钢板-混凝土复合梁横截面构造
1 裂缝间距计算
受弯的矩形带肋钢板-混凝土复合梁如图2。

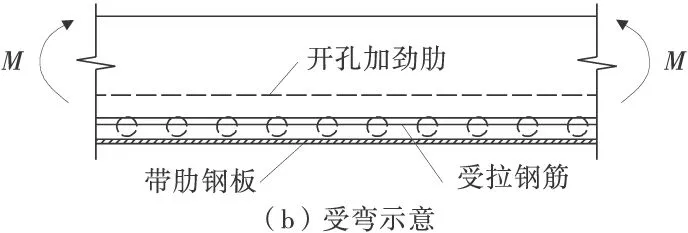
图2 矩形带肋钢板-混凝土复合梁受弯
参照钢筋混凝土裂缝计算的粘结-滑移理论[7],推导复合梁的裂缝间距。对矩形带肋钢板-混凝土复合梁受弯作如下基本假设:
1)取截面下部的h/2部分为受拉区;
2)截面开裂后,裂缝处受拉区混凝土退出工作,应力释放为0;
3)截面开裂后,未开裂截面混凝土拉应力大小沿截面高度不变,均为抗拉强度值ft;
4)自裂缝截面沿梁轴线,钢筋和带肋钢板与混凝土的黏结应力传递长度相同,均为l,即假设最小裂缝间距为l;
5)不考虑开孔加劲肋开孔高度范围内的钢板作用。
取长度为l、高度为h/2的一段矩形带肋钢板-混凝土复合梁为隔离体,隔离体一端为裂缝截面,另一端为未开裂截面,如图3。
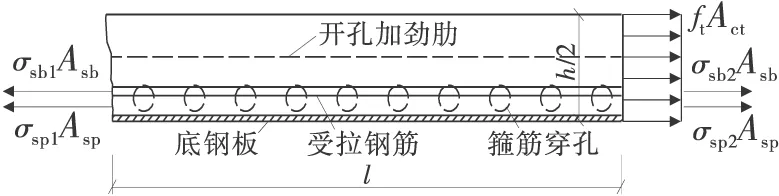
图3 RSCC梁受拉区隔离体受力示意
由受力平衡条件可得:
σsb1Asb+σsp1Asp=σsb2Asb+σsp2Asp+ftAct
(1)
在受拉区隔离体中单独取出钢筋作为隔离体,其受力如图4。

图4 钢筋隔离体受力示意
钢筋左右两端的拉力大小不平衡,因此由沿钢筋长度方向的黏结力来平衡,由受力平衡有:
(2)

同理,在受拉区隔离体中单独取出带肋钢板作为隔离体,其受力如图5。
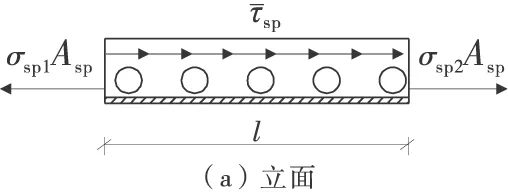
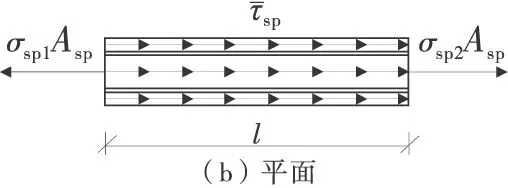
图5 带肋钢板隔离体受力示意
带肋钢板左右两端的拉力大小不平衡,因此由长度方向的粘结力来平衡,由受力平衡有:
(3)

整理式(1)~式(3)可得:
(4)
式中:ρ为截面的综合配筋(钢)率,ρ=(Asb+Asp)/Act;d为受拉钢筋直径。

(5)
令de=ηd,称de为设置了带肋钢板后的钢板和受拉钢筋的综合等效直径,则式(5)变换为:
(6)
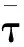
(7)
令总的配钢面积为As=Asb+Asp。
钢与混凝土接触面的总周长为u=usb+usp=nπd+b+4(hs-D),则等效直径de为:
(8)
对于相同截面、相同配筋率的普通钢筋混凝土梁,即配钢量As相同的条件下,假设所配钢筋直径为dRC,钢筋数量为nRC,则钢筋总周长为uRC=nRCπdRC,同时有
相同面积下,矩形的周长比圆形的周长大,因此设置了带肋钢板的RSCC梁中钢与混凝土接触总周长u,较只配置了受拉钢筋的普通钢筋混凝土梁中的钢筋总周长uRC大,于是有
可以得到
(9)
式(9)在理论上说明了,在相同配筋率下RSCC复合梁的裂缝间距较普通钢筋混凝土要小,同时也验证了文献[9]中的试验现象。再由无滑移理论,考虑加劲肋到混凝土表面的距离c对裂缝间距的影响,笔者提出综合考虑粘结-滑移理论和无滑移理论的裂缝间距计算式
(10)
2 加劲肋钢板顶部应变计算
在实验中,试验梁的起裂位置在高度上与纵向加劲肋顶位置所对应的高度基本相同,因此笔者主要讨论梁侧面对应于加劲肋顶的裂缝宽度。
结合RSCC梁受弯试验现象作以下基本假设:
1)RSCC梁受弯开裂后,横截面沿高度方向的宏观应变分布仍然满足平截面假定;
2)截面开裂后,裂缝处受拉区混凝土退出工作,应力释放为0;
3)RSCC梁带裂缝工作时,受力较小,带肋底钢板、加劲肋钢板、纵向受力钢筋和受压区混凝土应力、应变均处于线弹性阶段;
4)带肋钢板全部位于受拉区,即横截面中性轴位于加劲肋以上的混凝土范围内。
由基本假定,可得RSCC梁裂缝截面应力、应变分布如图6。
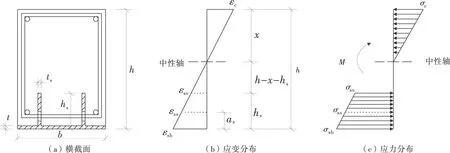
图6 RSCC梁裂缝截面应力、应变分布
2.1 几何关系
根据图6(b)的应变分布,可得到如式(11)的几何关系:
(11)
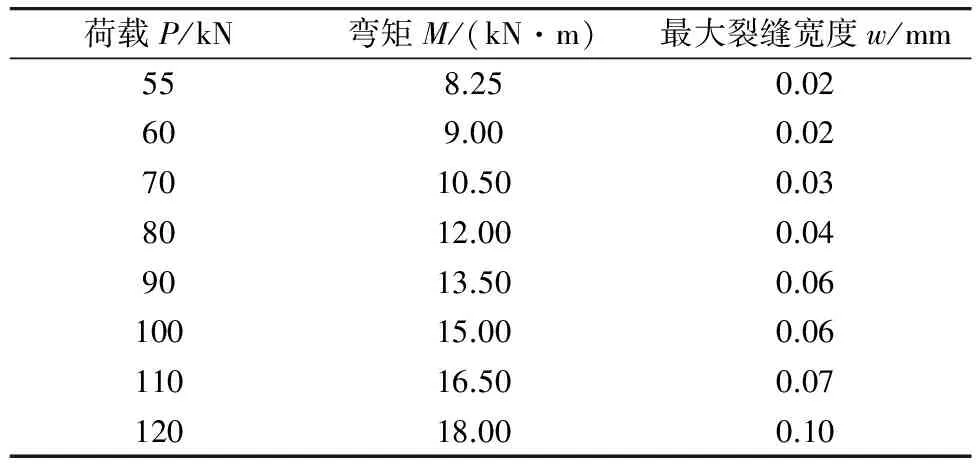
式中:εsu为加劲肋钢板顶部应变;εsb为底钢板应变,因底钢板厚度t< 2.2 物理关系 受压区边缘混凝土的应力大小 (12) 加劲肋钢板顶部应力大小 σsu=Esεsu (13) 加劲肋钢板底部应力大小,与底钢板应力大小相同 (14) 受拉钢筋应力大小 (15) 2.3 静力平衡条件 2.3.1 水平方向受力平衡 (16) 式中:b为截面宽度;hs为加劲肋高度;ts为加劲肋厚度;t为底钢板厚度;Ass为受拉钢筋截面总面积。 将式(12)~式(15)代入式(16),可得: (17) 式中:αE=Es/Ec。 2.3.2 截面力矩平衡 设截面所受弯矩为M,截面各部分力对截面中性轴取矩,可得: (18) 联立式(12)~式(15)、式(17)~式(18)可得裂缝处加劲肋钢板顶部应变计算式 (19) 在得到裂缝间距l和加劲肋钢板顶部应变εsu后,平均裂缝宽度计算式为 (20) 考虑混凝土裂缝间距和裂缝宽度的离散性,引入最大裂缝宽度与平均裂缝宽度的比值cp=ωmax/ωm,由裂缝试验数据统计,按95%的保证率取cp=1.645[13]。则对于矩形带肋钢板-混凝土复合梁,最大裂缝宽度计算式为 (21) 本次研究前期进行了5片RSCC试验梁,1片用于比较的常规粘贴钢板的钢筋混凝土梁和1片同配筋普通钢筋混凝土试验梁的受弯试验[9]。纯弯加载试验如图7,采用三分点对称加载的方式。反力架安放于加载位置,使用千斤顶进行加载,千斤顶置于反力架和试验梁之间,荷载通过分配梁传递到梁顶加载点。 图7 纯弯试验加载 试验结果显示,RSCC试验梁的开裂弯矩较普通钢筋混凝土试验梁提高了2倍多,在同等配筋率下,RSCC复合梁较普通钢筋混凝土梁能显著提高梁自身的开裂弯矩和开裂荷载。RSCC试验梁荷载试验数据如表1,由此可回归得到试验参数k1的具体数值。 表1 RSCC试验梁荷载-裂缝宽度 计算出各级荷载下的加劲肋钢板顶部应变εsu,和裂缝间加劲肋钢板应变不均匀系数φsr,以两者乘积φsrεsu为自变量,各级荷载下的最大裂缝宽度为因变量,k1为系数,应用MATLAB曲线拟合工具箱,拟合得到k1=4.4,拟合效果见图8。 图8 平均应变-最大裂缝宽度拟合 即有矩形带肋钢板-混凝土复合梁最大裂缝宽度计算公式: (22) 参照普通钢筋混凝土裂缝计算的粘结-滑移理论,考虑加劲肋到混凝土表面的距离c对裂缝的影响,提出综合考虑粘结-滑移理论和无滑移理论的裂缝间距公式,从理论上说明了在相同配筋率下,RSCC复合梁的裂缝间距较普通钢筋混凝土要小,同时也验证和解释了试验中的相关现象。在基本力学假设的前提下,推导了RSCC梁开裂截面加劲肋钢板顶部应变计算公式。在这两者的基础上,参照普通钢筋混凝土裂缝计算的综合理论给出了RSCC梁的最大裂缝宽度计算公式,并通过试验数据拟合得到了相关参数,为相关工程实践和研究工作提供了较好的参考。 [1] 高轩能,周期源,陈明华.黏钢加固RC梁承载性能的理论和试验研究[J].土木工程学报,2006,39(8):38-44.GaoXuanneng,ZhouQiyuan,ChenMinghua.TheoreticalandexperimentalresearchonbearingbehaviorofRCbeamsstrengthenedbybondedsteelplates[J].ChinaCivilEngineeringJournal,2006,39(8):38-44. [2] Saligar R.High grade steel in reinforced concrete[C]// 2nd Congress of IABSE.Berlin-Munich:IABSE Publication,1936:678-692. [3] Borges J F,Lima J A.Formation of Cracks in Beams with Low Percentage of Reinforcement [M].Stockholm:RILEM,1957:1125- 1136. [4] Base G D.Crack Control in Reinforced Concrete-Present Position[M].Melbourne:Symposium on Serviceability of Concrete,1975:452-466. [5] Broms B B.Stress distribution in reinforced members with tension cracks[J].American Concrete Institute,1965,62(9):1095-1108. [6] Broms B B.Crack width and spacing in reinforced concrete members [J].American Concrete Institute,1965,62(10):1237-1256. [7] 王传志,滕智明.钢筋混凝土结构理论[M].北京:中国建筑工业出版社,1985:304-307. Wang Chuanzhi,Teng Zhiming.Reinforced Concrete Structure Theory[M].Beijing:China Architecture & Building Press,1985:304-307. [8] 范亮.钢箱-混凝土组合拱截面受力行为与设计原理研究[D].成都:西南交通大学,2010:73-76. Fan Liang.Study on The Mechanical Behaviors and Design Principles of Steel Box-Concrete Composite Arch Sections[D].Chengdu:Southwest Jiaotong University,2010:73-76. [9] 徐勇,周志祥.带肋钢板-混凝土组合受弯构件抗裂性能试验研究[J].建筑结构,2014,9(9):29-33. Xu Yong,Zhou Zhixiang.Experimental study on the cracking resistance of steel plate reinforced concrete section with perforated stiffening rib plates [J].Chinese Journal of Building Structure,2014,9(9):29-33. [10] Hyung K R,Sung P C,Young J K,et al.Crack control of a steel and concrete composite plate girder with prefabricated slabs under hogging moments[J].Engineering Structures,2005,27(11):1613-1624. [11] Ziari A,Kianoush M R.Investigation of direct tension cracking and leakage in RC elements[J].Engineering Structures,2009,31(2):466-474. [12] Theiner Y,Hofstetter G.Numerical prediction of crack propagation and crack widths in concrete structures[J].Engineering Structures,2013,57(3):306-326. [13] Colotti V,Spadea G.An analytical model for crack control in reinforced concrete elements under combined forces[J].Cement and Concrete Composites,2005,27(4):503-514. [14] 姚国文,陈勇.在役桁式组合拱桥承载力评估与加固方法研究[J].重庆交通大学学报:自然科学版,2012,31(增刊1):696-699. Yao Guowen,Chen Yong.Evaluation of load capacity and strengthening methods for deteriorating trussed combination arch bridges[J].Journal of Chongqing Jiaotong University:Natural Science,2012,31(Sup1):696-699. Crack Width Calculation Method of Ribbed Steel-Concrete Composite Beam Wang Xiaodong1, 2, Wei Wenlong3, Tang Liang3 (1. Wuhan University of Technology, Wuhan 430070, Hubei, China; 2. Traffic Survey & Design Institute of Tibet Autonomous Region, Lhasa 850001, Tibet, China; 3. School of Civil Engineering & Architecture, Chongqing Jiaotong University, Chongqing 400074, China) Referring to the bond-slip theory of reinforced concrete cracks calculation method, crack spacing formula of the rectangular Ribbed Steel-Concrete Composite beam (RSCC beam) and strain formula of the top of stiffen plate were developed. The formulas explain the phenomena: the crack spacing of RSCC beam is smaller than that of ordinary reinforced concrete beams in the experiment. Referring to the calculation of ordinary reinforced concrete cracks comprehensive theory, the formula for calculating the maximum crack width of RSCC beam was derived. bridge engineering;crack width; cracking moment; ribbed steel-concrete composite beam; enhancement mechanism 10.3969/j.issn.1674-0696.2015.03.04 2014-09-14; 2014-10-29 国家自然科学基金项目(11302271);重庆市应用开发计划项目(cstc2013yykfB0123);重庆交通大学山区桥梁与隧道工程国家重点实验室培育基地开放基金项目(CQSLBF-Y13-8) 王晓东(1972—),男,山东胶州人,高级工程师,主要从事组合结构设计方面的研究。E-mail:tibetxd@qq.com。 U441 A 1674-0696(2015)03-016-05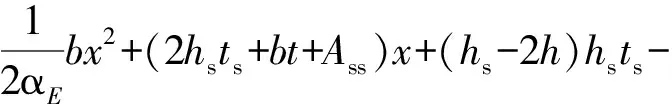
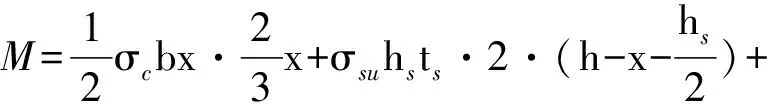
3 裂缝宽度计算



4 结 语

