“三十六计”对小学数学设问策略的一些启示

陈贻胜

摘 要：在小学数学教学活动中，教师可巧妙运用“三十六计”中所蕴含的智慧和策略，对学生回答问题进行科学设问，在识微见几中找准思维支点；在侧翼出击中培养创新精神；在蓄势而发中孕育破竹之气；在先退后进中共舞师生角色，以调整教学流程，修正教学方向，确保教学的高效顺畅，提高课堂教学的有效性。

关键词：小学数学；课堂教学；科学理答；教学流程；教学方向；有效性

中图分类号：G623.5 文献标识码：A 文章编号：1009-010X（2015）05-0059-05

堪称“益智之荟萃、谋略之大成”的《三十六计》是我国古代卓越的军事思想和丰富的斗争经验总结，虽无准确的年代和撰者可考，但其中的韬略计谋所折射的智慧至今仍在众多领域有效地沿用，教育教学亦不例外。教学活动中，教师如能巧妙运用“三十六计”中所蕴含的智慧和策略，对学生回答问题进行科学设问，有利于及时厘清教学线索，调整教学流程，修正教学方向，也有利于教师及时调控课堂，关注教学细节，确保教学的高效顺畅，提高课堂教学的有效性。

一、识微见几，以本为先

“经正而后纬成，理定而后辞扬。”明确问题的本质属性和关键症结是有效解决问题的重要前提。教师应在把握数学知识本质和知识发展主线的基础上科学地提出问题，并围绕问题本质进行设问，有效找准思维的支点，使学生对新知的认识由浅入深，进而掌握问题的实质。

（一）擒贼擒王

教学新知从关键处入手，就起到了提纲挈领的作用，能促进教学目标的有效达成。因此，教师应在“擒王”二字上着力，通过问题情境抓住关键信息设计问题，并有效理答，采取引问、追问等方式，让学生在不断渐进的“补充—明晰”过程中加深理解新知。

例如，进行“折扣”教学时，出示商场几个专柜促销广告：

师：以上信息，你对哪个词语不太熟悉？（生答“八折”）

师：猜一猜，八折是什么意思？

生1：“八折”表示现价是原价的。

师：能举个例子吗？

生1：假如某件商品原价10元，现价只需8元；某件商品原价100元，现价只需80元。

师：“八折”还能用别的数表示吗？

生2：还可以说成现价是原价的80%。

师：谁能用百分数和分数解释一下“三折”和“七五折”的意思？

生3：“三折”就是现价是原价的，也就是30%。

生4：“七五折”就是现价是原价的，也是75%。

师：真不错，居然还用上这样的分数。那么“几折”到底表示什么意思？

生5：“几折”就是现价是原价的十分之几，也就是百分之几十。

（二）釜底抽薪

算法多样化是“以人为本”教育思想的重要表现，但在处理算法多样化与算法优化的关系上，许多教师往往陷入跋前疐后的两难境地。由于一味追求算法多样化，教学中往往出现放任自流、一发难收的现象。此时，教师应通过追问，洞察学生思维的原点，再通过转问，巧妙摒弃干扰学生思维的相关信息，以“抽薪止沸，剪草除根”聚焦问题关键，挖掘信息内涵，厘清思路，理顺思维，优化算法。正如叶澜教授所说“没有聚焦的发散是没有价值的，聚焦的目的是为了促进学生发展。”

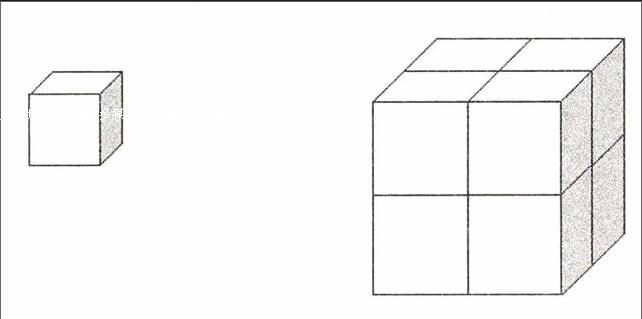
例如“正方体表面积”练习教学：如图，用8个表面积都是16平方厘米的小正方体拼成一个大正方体，大正方体表面积是多少平方厘米？

师：谁能说说你是怎么想的？

生1：先求小正方体一个面的面积，再计算大正方体表面积， 16÷6×4×6=64平方厘米。

生2：用8个小正方体表面积总和减去每个小正方体隐藏的表面积， 16×8-（16÷6）×3×8=64平方厘米。

生3：8个小正方体露在外面的面积之和就是大正方体表面积，16÷2×8=64平方厘米。

师：如果不知道小正方体表面积，能推算出大小正方体的表面积的关系吗？

生5：大正方体一个面的面积就是小正方体表面积的，×6=4，即大正方体表面积是小正方体的4倍。

生6：小正方体表面有6个小正方形，大正方体表面有24个小正方形，24÷6=4，大正方体表面积是小正方体的4倍。

生7：从正面看，小正方体有1个小正方形，大正方体有4个小正方形，其他的面也是这样，因此，大正方体表面积是小正方体的4倍。

师：如果小正方体表面积是16平方厘米，你最喜欢哪种算法？

生：16×4=64平方厘米。

二、侧翼出击，以迂为直

数学学习是两点之间的一条曲线。曲无定线，但过程应该是美的，正如《数学课程标准（2011版）》所指出的，数学活动经验需要在“做”的过程中积淀，是在数学学习活动过程中逐步积累的。因为有困惑，所以有曲折；因为有经历，才会有经验。引导学生经历数学的过程，往往以迂回策略去获取，以变换角度去思索，更有利于培养学生创新精神。

（一）声东击西

由于小学生心理发展不成熟，如果没有外界的刺激，他们往往会对新生知识坚持一些片面或是错误的理解，甚至会表现出“不撞南墙不回头”的精神。因此，把外在刺激与学生原有反映结构之间建立联系，才是学习活动的实质。教师在教学中可直接把“南墙”毫不避讳地展现出来，让学生“撞一撞”，“声言击东，其实击西”，及时采取提示、逆转的理答策略，让思维在错误与正确之间进行激烈交锋。

师：大家喜欢哪种方法？为什么喜欢这种方法？

生1：第一种方法算起来简单，只用计算4÷2，第二种方法要把除法转化成乘法，还要把除数变换成它的倒数。

师：如果把这张纸的平均分成3份，每份是这张纸的几分之几？你能用第一种方法试着解决吗？（当学生列出算式但不得其解，就问：有什么问题吗？）

生2： 4÷3的商不是整数。

师：那你现在还觉得第一种方法简单吗？

生3：我想用第二种方法试一试。

师；看来大家得重新研究了，还是再来折一折吧！

（二）欲擒故纵

《孙子兵法之军争篇》中“以迂为直，以患为利”这句话告诉我们，教师可以不直面学生认知盲点，采取旁敲侧击以达成教学目标。“欲擒故纵”则正是如此。与“声东击西”不同的是，前者侧重先否定一种思路再另辟蹊径，后者侧重两种思路的并举。“擒”为达成目标，“纵”为教学手段。

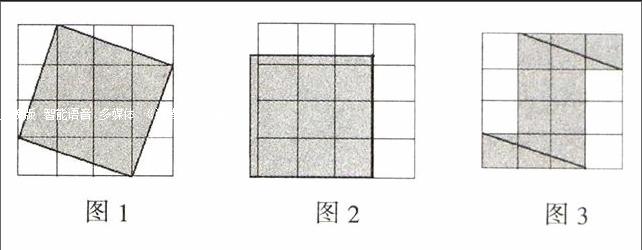
例如，“分数的再认识”练习教学：用分数表示图中的涂色部分（如右图1）。

师：谁能把自己的想法表达出来？

生1：涂色部分是正方形，边长是3，面积就是9，而整个图形的面积是16，所以，涂色部分占整个图形的■。（大部分学生表示同意）

教师不置可否，而是漫不经心地说： 涂色正方形站姿歪斜，大家若能不厌其烦地去观察，让它端正姿势，岂不更好？

生2：可以把涂色图形旋转，刚好与大正方形的9个空格重合。

师：你能从图形旋转上去思考，不错！

教师演示课件（如下图2），旋转后学生惊呼：啊，怎么会这样！

师：能找到刚才大家的想法错在哪吗？

生3：涂色正方形的边是直角三角形的斜边，比3格要长一些。

师：不错，但是旋转的方法应该给我们很多启示，不妨从图形的旋转和剪拼上再想想看。

三、蓄势而发，因势而为

蓄势者，方显破竹之气；顺势者，方能舒展思维。“用教材教”的理念告诉我们，教师只有对教材反复审视和科学重组，顺学生生活经验之“势”，顺学生认知特点之“势”，顺教师教学风格之“势”，才可能因势而为，顺藤摸瓜。

（一）浑水摸鱼

“浑水”是指学生回答模糊，虽没有明显错误但又不能指向问题核心的一种问题反馈现象，“摸鱼”是指教师应及时充当引导者和合作者的角色，在学生形形色色的片面回答中进行科学梳理，积极寻求有价值的反馈信息，帮助学生过滤和明晰，促进学生建构新知。教师运用此策略忌讳“隔岸观火”，置身事外。

例如“认识角”教学，教师设计了摸角的体验活动，采用肢体语言进行理答，让抽象和具体对接，使体验与建构同行。过程如下：先让学生在装有些许物品的袋子里摸角，体验角的感觉，然后教师在学生提示下摸角。

师：谁能给老师提示一下摸到角的感觉呢？

生1：角是尖尖的，很扎手。

教师摸出一个钉子，随即摇头。

生2：顺着尖头摸，会分有两边的。

教师摸出了一支铅笔，还是摇头。

生3：两边不能是圆圆的，而是摸起来有点割手的。

教师又在袋子里摸出了一片树叶，显得有些着急。

生齐声：角的两边还应该是直直的。

教师在学生的提示下终于摸出了角。

（二）顺手牵羊

教学中，由于学习个体的差异，一些学生的回答往往会偏离既定的轨道，此时教师放任自流，学生会渐行渐远。古人云，“遇时不疑。”机遇稍纵即逝，教师要以敏锐的洞察力果断获取有价值的线索，通过提示、过渡、转问的方式重新导向，引导学生进入绿色的探索之道。

例如“乘法估算”教学，出示图片：学生排队做操，大约有多少学生？问题一提出，大部分学生立即数了起来。

生1：每行有16人，有6行，共有96人。

生2：题目提出是大约有多少人，所以应该说大约是100人。

生3：数起来这么方便，干嘛要说大约人数呢？

人数少就不用估计了吗？学生的估算意识在哪里？

教师顺势引导：如果我们学校的学生都来到操场上做操，估计有多少人，你还要数吗？

生3：那数起来就太麻烦了。

生4：可以先数一个班的人数，再看全校一共有几个班？

生3反驳说：可是每个班的人数不一样呀？

师顺便插话：那看来没办法估计全校人数了。

生4申辩说：反正是估，只要大约数字就行了。

师：除了先估计一个班的人数，还可以通过什么来估计？

生5：可以先数每一行有多少人，再看有几行。

四、先退后进，以探定导

教学活动中，除了让学生获取具体的数学知识和结论之外，更重要的目的是其数学思维得到发展，这在某种意义上更依赖于学生对于数学活动的参与，对于具体数学对象的直接经验。学习主体地位要突出，教师自然要让位于学生的探究，要做到毫不眷恋地退出，而在学生的探究即将受阻时，又要适时地介入，运用巧妙的手段为学生的探究搭建有效的“脚手架”。

（一）以逸待劳

“劳”即以学生的自主探究为中心，“逸”就是要老师静观其变，“待”当然不是指消极被动地等待，而是知道时机不成熟时要能勇敢地退，在学生逐渐明确问题本质时，再通过提示性的过渡语引导学生提升认知。

例如“圆的认识”教学，教师让学生拿出一张圆形纸片，找出它的圆心、半径和直径。学生操作后汇报如下：

生1：（边演示边介绍）对折再对折，交叉点就是圆心。

生2：我是用圆规在圆纸片上比划出来的。

生3：一直对折下去，展开后就会发现许多半径。通过折痕重合就知道半径都是相等的。

生4：我在圆片上画出了许多条半径，如果我不停地画下去，就会画出无数条半径。我量了量，半径都是相等的。

生5：我是用圆规比出来的。圆规两脚间的距离其实就是半径的长度，所以应该都是相等的。

生6：通过圆心的折痕就是直径。像这样把圆纸片多次对折，就会折出许多条直径，所以直径也有无数条。

生7：对。每一条直径里面都包含两条半径。

师此时才插话并引导：居然有这么多的发现，真是了不起。看来动手操作是发现数学知识的好方法。既然半径和直径是有联系的，谁能用简洁的话说一说两者之间的关系呢？

生8：直径是半径的2倍，半径是直径的。

师：别急着下结论，先动手比一比再说吧。可以自己比，也可以和周围同学互相比。

由于学生之间的圆大小不一致，通过学生的动手比较，很快就认识到“同一圆内”或“相等的圆内”才是这一结论的前提。

（二）金蝉脱壳

如果说“以逸待劳”是教师与生共舞，那么“金蝉脱壳”则是教师顺势而退。当课堂已经属于学生的天地时，教师的引导应戛然而止，坚定地从“壳”里走出，这样教师因完成自我而更加美丽，学生因不断超越而显得无比精彩。

生：不一定！如果小明的零花钱比小芳多，小明可能就捐得多了。

师：能举例说一说吗？

师：很有道理，看来小明捐的钱一定比小芳多。

众生：不一定，还有其他可能。

师：是吗？我都搞糊涂了！干脆来捋一捋，男生扮演小明，女生扮演小芳，每人拿出课前准备的不同张数的小正方形纸片，假若每张表示10元，数一数自己的“零花钱”，再想好你零花钱的或，然后比一比。

“求木之长者，必固其根本；欲流之远者，必浚其泉源。”根须植，源必浚。课堂是促进学生发展的主要阵地，理答是学生获取发展的有效途径。无论是哪种理答策略，最终都是积极引导学生在“学会”的过程中向“会学”迈进。教师在追寻更有效的教学道路上求索，需要不断研究和反思更有效的设问行为，赋予课堂更多的精彩，也赋予学生更广阔的发展空间。

参考文献：

[1]李汉秋.《孙子兵法》与《三十六计》品读[M].云南：云南教育出版社，2008：96～180.

[2]陈超群.小学数学教师理答行为的观察研究[J].中小学数学（小学版），2013，（7～8）：6～7.

[3]王光明，范文贵.新版课程标准解析与教学指导（小学数学）[M].北京：北京师范大学出版社，2012：143.

[4]劳凯声.教育学[M].天津：南开大学出版社，2001：115.

[5]范艳华.以学定教，以教导学教学模式和课型的选择和应用（小学数学）[M].长春：东北师范大学出版社，2014：14.