数学思维灵活性的培养

杜连友

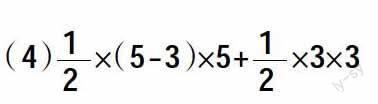
摘 要：思维品质主要包括敏捷性、灵活性、深刻性、独创性和判断性五个方面。这五个方面反映了人与人之间思维的个性差异，是确定一个人智力水平能力的主要指标。培养思维品质是发展思维能力的突破点，是提高教育质量的途径。由此可见，我们在数学教学中必须把培养数学思维品质这一工作放在至关重要的位置。

关键词：数学；思维；品质；灵活性；培养

思维的灵活性集中反映了从一种思维方向迅速转移到另一种思维方向的能力。从数学角度考虑，它至少应有以下特点：（1）起点灵活；（2）思维过程灵活；（3）概括迁移能力强。所以，为了让学生思维灵活，就必须设法让学生的思维在以下几方面下功夫。

一、启发学生多角度思考，多途径解题，做到起点灵活

引导学生解题的第一的环节便是启发学生从多角度去思考，多途径去想办法解题，做到起点灵活。

例1. 某工人4小时加工零件20个，照这样计算，12小时加工零件多少个？

正归一法：30÷5×14=60（个）

反归一法：12÷（4÷20）=60（个）

倍比法：20×（12÷4）=60（个）

比例法：解：设12小时加工零件x个，20 ∶ 4=x ∶ 12

例2. 两个正方形，一个边长是5厘米，另一个边长是3厘米，求阴影部分的面积，通过引导学生从不同角度不同方法思考可得以下解法。

（1）5×5+3×3-5×5÷2-（5+3）×3÷2

（2）（3+5+3）×5÷2-（5+3）×3÷2-（5-3）×3

（3）[5×5+3×3+（5-3）×3]-5×5÷2-（5+3）×3÷2-（5-3）×3

（4）×（5-3）×5+×3×3

在数学教学中，有意识地收集这样的题目，并时时有意识地训练学生，使他们养成从多角度考虑问题，多途径解决问题的习惯，从而达到起点灵活的目的。

二、克服定势，根据新的信息，及时调整解题策略，做到思维过程灵活

例3. 某工厂有男工80人，女工20人，男女工共有多少人？

把“女工20人”这一条件隐藏起来，变为间接条件放入题中，逐层补充新的条件：（1）女工比男工少60人，（2）男工比女工多60人，（3）男工是女工的4倍，（4）女工比男工的2倍少140人。

引導学生将前后变化的题目进行认真分析，从其结构、数量关系等方面寻找联系和变化，捕捉解题规律。

三、注意概括总结，努力促进迁移，做到灵活学习

灵活地学习，就应该善于在已知的数学关系中得出关系，在学习新的数学知识时，又善于综合、分析，通过概括，促进知识的系统化，从而适用于新的情境。

以上三种方面粗略地论述了数学思维灵活培养的问题，其方法是多种多样的。总之，在数学教学中，只要时时有意识地训练学生，就一定能培养学生的思维灵活性，使他的智力得到充分地发展。

编辑 郑 淼