具有阶段结构的捕食系统的全局渐近稳定性

傅秋月， 魏凤英

(福州大学数学与计算机科学学院， 福建 福州 350116)

具有阶段结构的捕食系统的全局渐近稳定性

傅秋月， 魏凤英

(福州大学数学与计算机科学学院， 福建 福州 350116)

研究一类捕食者与食饵均具有阶段结构的捕食模型的稳定性. 通过分析模型的特征根， 得到了非负平衡点局部稳定性的条件. 利用比较定理、 迭代方法等性质证明了非负平衡点的全局渐近稳定性. 并举实例说明所得结果的有效性.

全局渐近稳定性； 阶段结构； 捕食系统； 平衡点

0 引言

自然界中物种是多种多样的， 它们之间存在着很多种关系.例如捕食关系， 寄生关系， 竞争关系， 互惠合作关系等. 在这些关系中， 捕食关系是影响自然选择的主要因素之一， 它推动生态系统的稳定运行. 由于捕食系统存在的普遍性， 捕食者和食饵的动力学关系将继续成为生物数学上的主要研究课题[1-8]. 徐瑞等[2]研究了捕食者具有阶段结构的L-V时滞捕食系统

通过分析特征方程， 他们得到了非负平衡点局部稳定的条件， 并得到时滞τ超过某特定值τ0后， 正平衡点出现Hopf分支， 同时， 利用迭代方法证明了非负平衡点的全局稳定性.

近年来， 对于捕食者与食饵均具有阶段结构的捕食模型的动力学行为的研究较少[3, 5]. 桂占吉等[3]研究了具有阶段结构的捕食模型的稳定性及成年食饵种群的捕获， 并得到了正平衡点全局渐近稳定的充分条件和食饵种群的最大捕获量. 同时， 具有阶段结构的两种群竞争系统的动力学关系得到了许多学者的广泛研究[7-8]. 宋新宇等[7]研究了具阶段结构及成年捕获的两种群竞争模型:

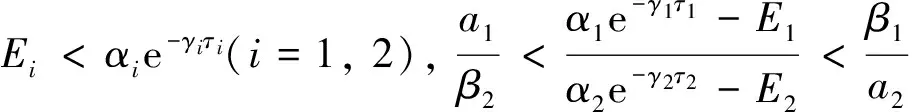
的非负平衡点的稳定性， 其中x1(t),x2(t)分别表示幼年食饵和成年食饵种群在t时刻的密度；y1(t),y2(t)分别表示幼年捕食者和成年捕食者种群在t时刻的密度；a11,a21,a22,b1,b2,r1,α,β,γ都是正常数；r1为幼年食饵的内禀增长率;a11和a21分别表示幼年食饵和成年食饵种群的死亡率；a22为成年食饵的种内竞争率；β为成年捕食者捕食成年食饵的捕获系数；τ1,τ2分别表示幼年食饵、 幼年捕食者成长为成年食饵与成年捕食者的时间； e-a11τ1x2(t-τ1)表示幼年食饵在t-τ1时刻出生， 并且在t时刻存活并转化为成年食饵的数量；α/β表示捕获成年食饵的营养转化率；γ和b1分别表示幼年和成年捕食者的死亡率；b2表示成年捕食者的过度拥挤所至死亡率； e-γτ2x2(t-τ2)y2(t-τ2)表示在t-τ2时刻出生的幼年捕食者在t时刻仍然存活， 且在t时刻转化为成年捕食者的数量.

1 预备知识

系统(3)的初始条件为

x1(θ)=φ1(θ),x2(θ)=φ2(θ),y1(θ)=φ3(θ),y2(θ)=φ4(θ),φi(θ)>0 (i=1, 2, 3, 4)

其中:θ∈[-τ, 0],τ=max{τ1,τ2}.R-=(-∞, 0],R+=[0, +∞).φi(θ)∈C([-τ, 0],R+)(i=1, 2, 3, 4)

由初始值的连续性， 进一步要求

引理1 对任意t≥0， 满足初值条件(4)～(5)的系统(3)的解为正解.

引理2 对任意t≥0， 满足初值条件(4)～(5)的系统(3)的正解为一致有界.

引理1的证明过程类似于文[2]定理2.1， 引理2的证明过程类似于文[3]引理1， 此处从略.

2 系统(3)的平衡点及其稳定性

本文假设以下条件成立

平衡点E0处的特征方程为(λ+a11)(λ+γ)(λ+b1)[λ+a21-r1e-τ1(λ+a11)]=0， 若(H1)成立， 则E0是稳定的； 若(H2)成立， 则E0是不稳定的.

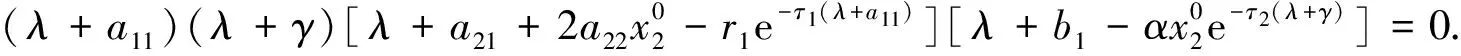
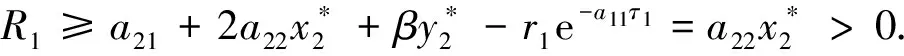
由比较定理， 存在T1>0, 使得x2(t)T1. 所以

应用引理3和比较定理， 存在T2>T‴1, 使得x2(t)T2， 于是

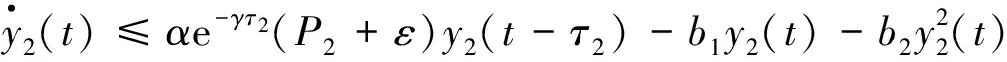
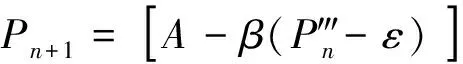
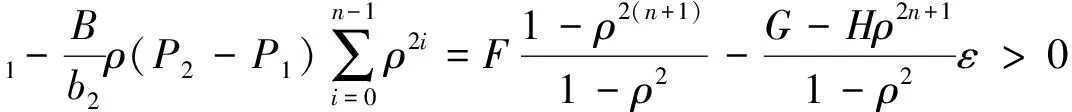
定理2 若(H1)成立， 则系统(3)的平衡点E0(0, 0, 0, 0)是全局渐近稳定的.

定理2， 定理3的证明过程类似于文[7]定理3.2, 3.3的证明过程， 此处从略.

3 数值模拟

考虑捕食者与食饵均具有阶段结构的捕食系统

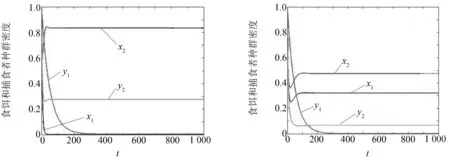
图全局渐近稳定( τ1=0.01, τ2=0.1)

4 结论

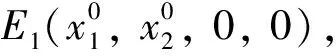
[1] Cushing J M. Periodic time-dependent predator-prey systems[J]. SIAM J Appl Math, 1977, 32(1): 82-95.

[2] Xu Rui, Chaplain M A J, Davidson F A. Global stability of a Lotka-Volterra type predator-prey model with stage structure and time delay[J]. Appl Math Comput, 2004, 159(3): 863-880.

[3] Gui Zhanji, Ge Weigao. The effect of harvesting on a predator-prey system with stage structure[J]. Ecol Modelling, 2005, 187(2/3): 329-340.

[4] Cai Liming, Song Xinyu. Permanence and stability of a predator-prey system with stage structure for predator[J]. J Comput Appl Math, 2007, 201(2): 356-366.

[5] 马智慧， 李自珍， 王淑璠. 具有阶段结构的捕食-食饵模型[J]. 兰州大学学报: 自然科学版， 2008, 44(2): 103-106.

[6] 热孜娅·托合提, 滕志东. 一类捕食者具有阶段结构的捕食被捕食系统的持久性[J]. 新疆大学学报: 自然科学版, 2012, 29(2): 157-162.

[7] Song Xinyu, Chen Lansun. Optimal harvesting and stability for a two-species competitive system with stage structure[J]. Math Biosci, 2001, 170(2)： 173-186.

[8] Liu Shengqiang, Chen Lansun, Luo Guilie,etal. Asymptotic behaviors of competitive Lotka-Volterra system with stage structure[J]. J Math Anal Appl, 2002, 271(1): 124-138.

(责任编辑： 林晓)

Globally asymptotic stability of predator-prey systems with stage structure

FU Qiuyue, WEI Fengying

(College of Mathematics and Computer Science， Fuzhou University， Fuzhou， Fujian 350116， China)

The stability of a kind of predator-prey models with stage structure for both predators and preys is considered in this paper. By analyzing the characteristic roots of the models, the conditions of local stability for nonnegative equilibrium are derived. By the comparison theorem and iteration method, we prove that nonnegative equilibrium of the models are globally asymptotic stable. An example is given to illustrate the effectiveness of our results．

globally asymptotic stability； stage structure； predator-prey systems； equilibrium

10.7631/issn.1000-2243.2015.04.0440

1000-2243(2015)04-0440-05

2013-05-05

魏凤英 (1976- ), 教授, 主要从事随机微分方程及生物数学研究， weifengying@fzu.edu.cn

国家自然科学基金资助项目(11201075); 福建省自然科学基金资助项目 (2010J01005)

O175.14

A