圆端形钢管混凝土轴压短柱的机理分析
谢恩普, 王志滨, 林 盛, 周继忠
(1. 福州大学土木工程学院, 福建 福州 350116; 2. 福建工程学院土木工程学院, 福建 福州 350118)
圆端形钢管混凝土轴压短柱的机理分析
谢恩普1, 王志滨1, 林 盛1, 周继忠2
(1. 福州大学土木工程学院, 福建 福州 350116; 2. 福建工程学院土木工程学院, 福建 福州 350118)
基于有限元软件ABAQUS对圆端形钢管混凝土轴压短柱进行分析. 分析表明: 圆端形钢管对核心混凝土的约束效果介于圆钢管和矩形钢管之间; 钢管对核心混凝土的约束作用主要分布于圆弧段; 圆端形钢管混凝土柱的承载力、 峰值应变和延性均介于圆钢管混凝土柱和矩形钢管混凝土柱之间; 圆端形钢管混凝土构件承载力和延性随着钢管强度、 含钢率、 加劲肋厚度和加劲肋数量的提高而提高; 随着混凝土强度的提高, 其承载力提高但延性下降.
圆端形钢管混凝土; 轴压; 约束力; 延性
0 引言
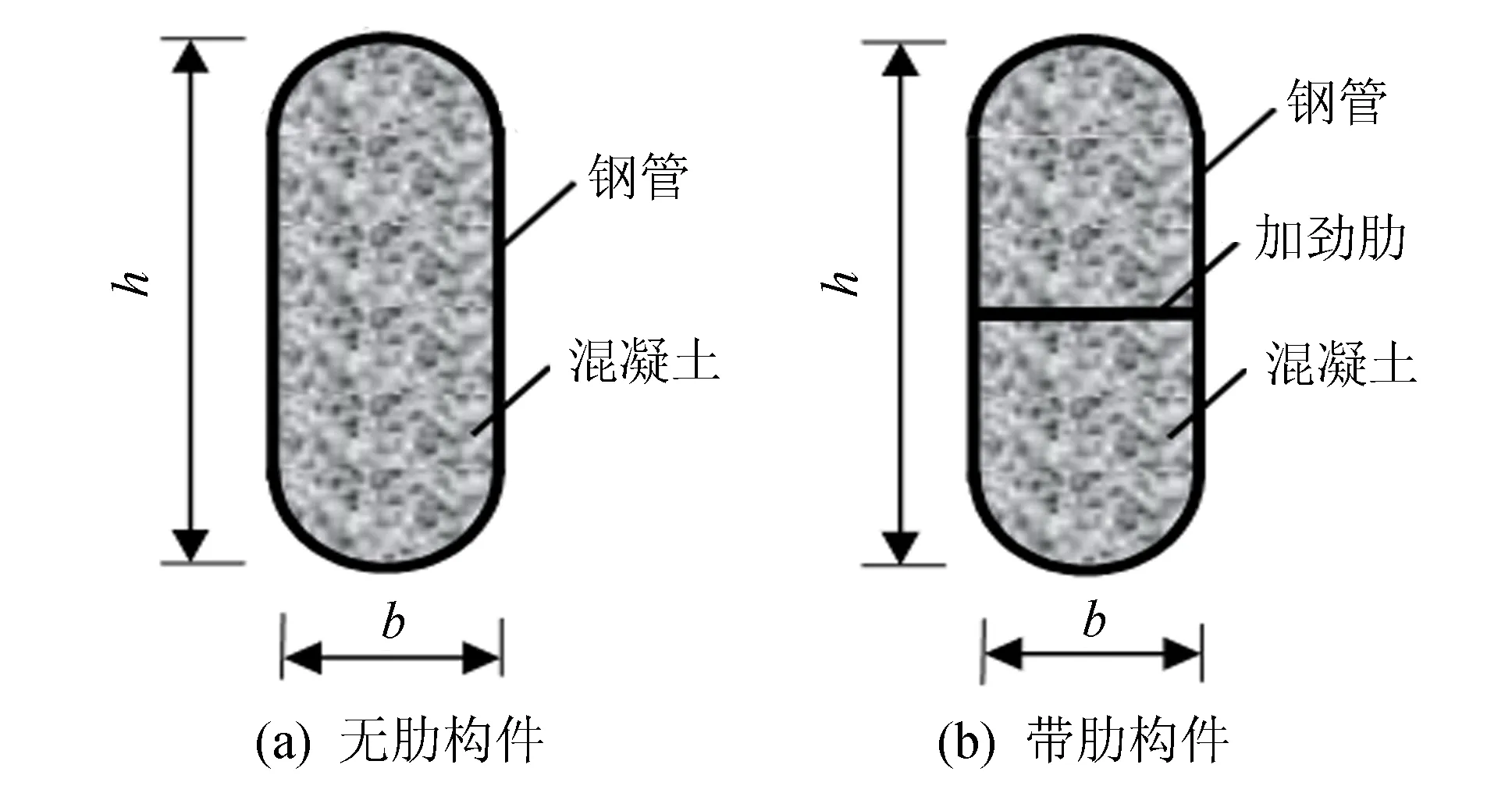
图1 典型圆端形钢管混凝土构件截面Fig.1 Cross-sections of typical concrete-filled round-end steel RHS columns
钢管混凝土由于承载力高、 抗震性能好和施工方便等特点已被广泛应用于桥梁工程中[1]. 同时, 为保证桥梁的横桥向刚度和顺桥向刚度相差不大, 桥梁的桥墩和立柱一般设计成圆端形截面. 圆端形钢管混凝土柱(典型截面形式如图1所示)同时具有以上两者的优点, 因此, 在人行天桥和市政工程的高架桥中有着广阔的应用前景. 该类新型构件已被应用于厦门杏林湾路段平台的边墩中.
文献[2]建议该类构件的构造措施. 文献[3]实测了实桥中圆端形钢管混凝土双肢主塔的应力分布.
文献[4]进行了圆端形中空夹层混凝土轴压直、 斜短柱的试验研究, 其钢管采用不锈钢管. 笔者所在的课题组进行了一系列圆端形钢管混凝土轴压短柱的试验研究, 并建议了精度较高的有限元模型, 最终建议了实用的承载力简化计算公式[5]. 在以上研究的基础上, 笔者认为尚需进一步开展深入的机理分析和参数分析.
1 有限元模型
1.1 材料本构
钢材采用文献[1]建议的二次塑流模型. 并采用ABAQUS的塑形损伤模型模拟混凝土, 混凝土单轴受压应力-应变关系为文献[1]建议的矩形钢管混凝土本构, 使用时将圆端形截面视为截面高、 宽分别为h和b, 截面转角半径为b/2的带转角的矩形截面. 混凝土模型具体如下:
式中各参数的计算方法详见文献[1].
1.2 接触关系、 单元种类以及边界条件
采用“硬接触”模拟钢管与混凝土的法向接触行为. 采用“库伦摩擦”模型模拟钢管与混凝土的切向接触行为, 摩擦系数μ取为0.6. 模型中钢管和纵向加劲肋采用S4R壳单元, 混凝土采用C3D8R实体单元. 除上端面的轴向位移外, 约束构件上下端面的其余5个自由度. 采用位移加载的控制模式, 在构件上端面施加轴向位移. 由于构件绕其弱轴的长细比较大, 在轴压力作用下构件可能发生整体稳定破坏. 因此, 在模型中取1/1 000杆长作为该类构件的初始偏心距[6].
1.3 模型验证
文献[5]已验证该模型的正确性, 图2仅列出部分模拟结果和试验实测结果的对比. 由图2可见, 该模型可用于圆端形钢管混凝土轴压短柱的受力全过程的模拟, 也可用于进一步的机理分析和参数分析.
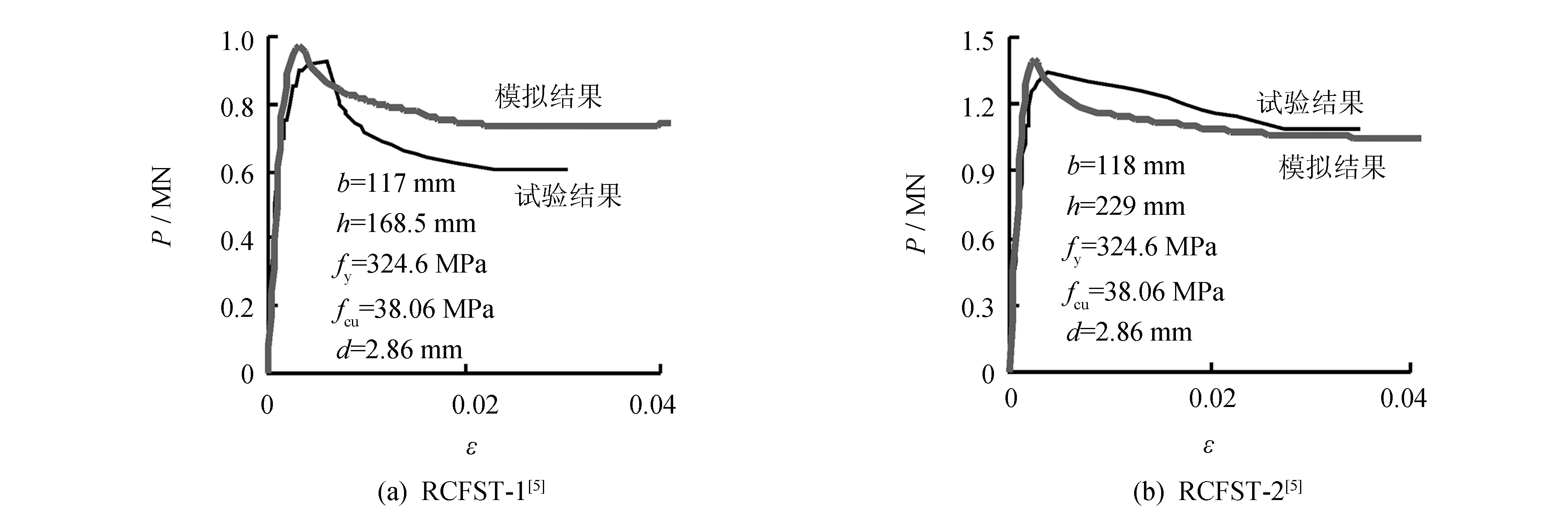
图2 P-ε曲线Fig.2 P-ε curves
2 机理分析
为深入分析圆端形钢管混凝土柱的工作机理, 首先进行典型构件的数值模拟. 典型算例基本参数为: 截面高度h=1 600 mm; 截面宽度b=800 mm; 构件长度l=4 800 mm; 钢管采用Q345; 混凝土采用C50; 截面含钢率为0.1; 钢管壁厚d=26 mm. 同时还给出了典型构件的对比空钢管的数值模拟结果.
2.1 破坏模态
钢管混凝土和对比空钢管的破坏模态列于图3中, 以上两种典型算例的破坏模态与文献[4]实测破坏模态较为接近. 空钢管发生交替向内和向外的严重局部屈曲. 由于受到核心混凝土的支撑作用, 钢管混凝土构件仅在跨中出现轻微的向外局部屈曲.
2.2 受力全过程分析
图4为典型算例的荷载-轴向应变关系曲线. 由图4可知: 峰值荷载作用时, 混凝土和钢管分别承担了60.79%和39.21%的荷载. 核心混凝土的峰值应变决定了构件的整体峰值应变, 典型算例的峰值应变为0.003 1, 该值大于素混凝土的峰值应变0.002 2, 这说明钢管的约束作用可改善混凝土的变形能力. 因为钢管存在环向应力, 故钢管屈服时其纵向应力小于345 MPa, 而空钢管的纵向应力等于345 MPa, 因此钢管混凝土达到峰值荷载时钢管所分担的荷载略小于空钢管的承载力. 由于受到核心混凝土的支撑作用, 钢管的峰值应变、 剩余承载力和延性明显高于对比空钢管.
由图4还可发现: 圆端形钢管混凝土轴压短柱的荷载-轴向应变曲线大致可分为三个阶段: ①弹性段OA,A点处钢管的纵向应力达到其比例极限; ②强化段AB,B点为峰值荷载; ③软化段BC,C点时轴向应变达到0.01.

图3 破坏模态Fig.3 Failure modes

图4 典型算例轴向荷载-应变关系曲线Fig.4 P-ε curves of typical numerical example
2.3 混凝土的应力状态
图5给出了典型构件跨中截面的混凝土纵向应力分布图, 图中fc为混凝土圆柱体强度. 由图5可发现如下规律: ① 混凝土的应力随着轴向应变的增大而增大. ② 峰值荷载作用时, 混凝土的纵向应力值均大于其圆柱体强度, 最大纵向应力值比圆柱体强度高47.6%, 原因是钢管对核心混凝土的约束作用有效的提高了混凝土的峰值应力. ③ 越靠近钢管圆弧段中点(O点), 混凝土的纵向应力值越大; 越靠近钢管平直段的中点(O′点), 混凝土的纵向应力值越小. 原因是钢管圆弧段对核心混凝土的约束作用大于钢管平直段. ④ 峰值荷载后混凝土软化, 其应力值明显下降, 但圆弧段范围内的混凝土的应力值仍然大于其圆柱体强度.

图5 混凝土应力分布Fig.5 Stress distribution of the concrete
2.4 钢管的应力状态
图6给出了典型构件的钢管纵向应力云图. 由图6可知: 由于端部受到约束, 端部的应力较小.A点时, 跨中截面的钢管应力值接近其比例极限. 峰值荷载作用时(B点), 钢管完全屈服, 在跨中截面由于环向应力的存在(最大值61.18 MPa), 其最大纵向应力值为325.5 MPa, 该值小于其屈服强度(fy=345 MPa). 当纵向应变达到0.01(C点)时, 由于局部屈曲的影响, 跨中截面的应力分布不均匀, 最大值为361 MPa, 最小值为68.02 MPa.

图6 钢管的应力分布(单位: MPa)Fig.6 Stress distribution of the steel tube(unit: MPa)
2.5 相互作用分析
图7给出了典型构件的法向接触应力分布图. 由图7可发现如下规律: ① 法向接触应力随着轴向应变的增大而增大. ② 整个钢管圆弧段的接触力分布较为均匀, 最大值出现在切点(O点)附近; 越靠近钢管平直段的中点(O′点), 接触应力越小. 这也是图5中钢管圆弧段范围混凝土峰值应力值较大的原因. ③ 峰值荷载作用后圆弧段范围内的接触应力进一步增大, 但钢管平直段范围内的接触应力明显减小. 原因是此时平直段钢管发生局部屈曲(如图3所示), 钢管和混凝土之间发生剥离.

图7 混凝土与钢管接触应力(单位: MPa)Fig.7 Contact stress between the concrete and the steel tube (unit: MPa)

图8 接触应力-轴向应变关系曲线Fig.8 Contact stress versus longitudinal strain curves
图8给出了钢管圆弧段中点、 圆弧段四分点和切点处混凝土-钢管之间法向接触应力-轴向应变曲线. 由图8可知: ①轴向应变小于0.006时, 法向接触应力值随轴向应变的增大而增大; 钢管圆弧段中点和四分点处的接触应力值大于切点处. ②轴向应变达到0.006后, 圆弧段的接触应力值的增速放缓; 切点处的接触应力值迅速下降. 原因是轴向应变达到0.006后钢管进入屈服阶段, 此时, 钢管环向应力和约束力的增速放缓. 而钢管切点因靠近钢管平直段, 受钢管局部屈曲的影响, 该处的约束力出现突降现象.
2.6 圆钢管混凝土、 矩形钢管混凝土和圆端形钢管混凝土的对比

图9 截面形状对P-ε关系曲线的影响Fig.9 Influence of cross sections on P-ε curves
为进一步分析截面形状对钢管混凝土轴压短柱力学性能的影响规律, 图9给出圆钢管混凝土、 圆端形钢管混凝土和同截面高宽比的矩形钢管混凝土荷载-轴向应变关系曲线. 其中, 组成钢管混凝土构件的混凝土面积、 钢管面积以及材料强度均相同.
由图9可发现如下规律: ① 圆形、 圆端形和矩形钢管混凝土峰值应变分别为0.005 9、 0.003 1和0.001 8. 这说明尽管圆端形钢管混凝土的峰值应变比圆钢管混凝土低47.6%, 但却比矩形钢管混凝土高68.8%. ② 圆钢管混凝土、 圆端形钢管混凝土和矩形钢管混凝土的极限承载力分别为93.619、 84.305和73.116 MN. 这说明, 尽管圆端形钢管混凝土的极限承载力比圆钢管混凝土低10%左右, 但却比矩形钢管混凝土高15.3%.
通过输出峰值荷载作用时的约束力, 可求得矩形钢管混凝土、 圆形钢管混凝土和圆端形钢管混凝土在峰值荷载作用时的平均约束力分别为2.79、 6.19和3.29 MPa. 这说明圆端形钢管对核心混凝土的约束效果介于矩形和圆形钢管之间, 也就解释了图9中圆端形钢管混凝土的峰值应变和承载力低于圆钢管混凝土, 但却高于矩形钢管混凝土的现象.
文献[6]中介绍了如下延性系数(DI)的计算方法:
其中:ε85%为荷载下降到极限荷载的85%时对应的轴向应变;εy=ε75%/0.75,ε75%为荷载上升到75%的极限荷载时对应的轴向应变.
通过图9三个典型算例的计算可知: 圆钢管混凝土达到0.04时承载力仍保持在85%以上, 因此其延性系数为无穷大; 圆端形钢管混凝土和矩形钢管混凝土的延性系数分别为2.425和2.33. 这说明尽管圆端形钢管混凝土的延性低于圆钢管混凝土, 但其延性系数仍比矩形钢管混凝土高4%左右.
3 参数分析
采用以上有限元模型对圆端形钢管混凝土轴压短柱进行参数分析. 主要参数包括混凝土强度、 钢管屈服强度、 加劲肋厚度、 截面含钢率和截面高宽比等. 除特别强调外, 典型算例的基本参数与上节机理分析典型算例均相同. 图10~图15给出了各参数对该类构件荷载(P)-轴向应变(ε)关系曲线的影响规律.

图10 钢管强度对P-ε曲线的 影响Fig.10 Influence of steel strength on P-ε curves

图11 混凝土强度对P-ε曲线的 影响Fig.11 Influence of concrete strength on P-ε curves

图12 截面含钢率对P-ε曲线的 影响Fig.12 Influence of steel ratio on P-ε curves

图13 加劲肋厚度对P-ε曲线的 影响Fig.13 Influence of stiffener thick- ness on P-ε curves
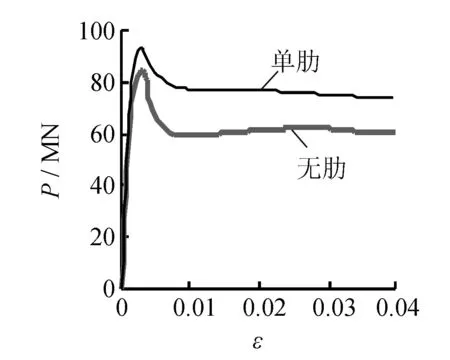
图14 肋数量对轴向P-ε 曲线的影响Fig.14 Influence of stiffener number on P-ε curves

图15 截面长宽比对P-ε曲线的 影响Fig.15 Influence of sectional aspect ratio on P-ε curves
由以上图形可看出: 当钢管屈服强度由235 MPa提高到500 MPa时, 构件承载力提高了46%, 承载力和峰值应变均得到了显著提高; 当混凝土立方体抗压强度由30 MPa提高到70 MPa时, 构件的承载力提高了54.5%; 当α由0.04提高到0.15时, 构件的承载力提高了56.7%; 当加劲肋数量由0提高到1时, 构件的承载力提高了13.4%, 且带肋构件的延性明显大于无肋构件; 当截面高宽比由1.5提高到2.5时, 构件的承载力仅下降了3.8%, 但其延性明显下降.
4 结语
1) 圆端形钢管混凝土中的钢管可对核心混凝土形成良好的约束, 有效约束主要集中在钢管圆弧段.
2) 内置混凝土可有效提高钢管的峰值应变、 剩余承载力和延性.
3) 圆端形钢管对核心混凝土的约束效果介于圆钢管和矩形钢管之间, 其承载力、 峰值应变和延性也介于圆钢管混凝土和矩形钢管混凝土之间.
4) 圆端形钢管混凝土轴压短柱的承载力和延性随着钢管强度、 含钢率、 加劲肋数量和加劲肋厚度的提高而提高; 随着混凝土强度的增大, 其承载力提高但延性下降; 随着截面高宽比的增大, 构件承载力和延性均降低.
[1] 韩林海. 钢管混凝土结构-理论与实践[M]. 2版. 北京: 科学出版社, 2007.
[2] 严定国, 黄纳新, 陈勇. 无砟轨道下1~80 m下乘式钢管混凝土拱桥设计[J]. 铁道工程学报, 2007, 12(Sup): 236-239.
[3] 谢建雄, 蔡崇华, 卢哲安, 任志刚. 微膨胀钢管混凝土双肢柱试验研究与数值模拟[J]. 武汉大学学报: 工学版, 2010, 43(4): 485-489.
[4] Han Linhai, Ren Qingxin, Li Wei. Test on stub stainless steel-concrete-carbon steel double skin tubular columns[J]. Journal of Constructional Steel Research, 2011, 67(9): 437-452.
[5] 王志滨, 陈靖, 谢恩普. 圆端形钢管混凝土柱的轴压力学性能研究[J]. 建筑结构学报, 2014, 35 (7): 123-130.
[6] Vivian W Y T, Wang Zhibin, Tao Zhong. Behaviour of recycled aggregate concrete filled stainless steel stub columns[J]. Materials and Structures, 2014, 47(1/2): 293-310.
(责任编辑: 沈芸)
Mechanism analysis on concrete-filled round-end steel tubular stub columns under axial load
XIE Enpu1, WANG Zhibin1, LIN Sheng1, ZHOU Jizhong2
(1. College of Civil Engineering, Fuzhou University, Fuzhou, Fujian 350116, China;2. College of Civil Engineering, Fujian University of Technology, Fuzhou, Fujian 350118, China)
The analysis on concrete-filled round-end steel tubular (CFREST) stub column under axial compression were carried out using finite element software ABAQUS. The analysis results indicate that: the confinement effect provided by the round-end steel tube is between those provided by circular and rectangular steel tubes. The confinement effect provided by the round-end steel tube on the core concrete is mainly distributed in arc segment. The strength, peak strain and ductility of the CFREST column are between those of the CFST column with circular and rectangular cross-sections. For CFREST columns, the strength and ductility increase with the increasing of the steel strength, steel ratio, stiffener thickness and the number of stiffeners. As the concrete strength increases, the strength increases but the ductility drops.
concrete-filled round-end steel tubular column; axial load; confinement; ductility
10.7631/issn.1000-2243.2015.04.0517
1000-2243(2015)04-0517-06
2014-01-28
王志滨(1979-), 博士, 讲师, 主要从事组合结构研究, wangzhibin@fzu.edu.cn
国家自然科学基金资助项目(51308124); 福建省自然科学基金资助项目(2013J05073, 2012D075)
TU352.1
A

