基于ACO-LSSVM燃煤碳元素分析的锅炉CO2排放量计算

许巧玲, 王彦端， 林伟豪, 梁 航， 万 晋

(1. 福州大学石油化工学院， 福建 福州 350116； 2. 福建省锅炉压力容器检验研究院， 福建 福州 350008)

基于ACO-LSSVM燃煤碳元素分析的锅炉CO2排放量计算

许巧玲1, 王彦端1， 林伟豪2, 梁 航2， 万 晋1

(1. 福州大学石油化工学院， 福建 福州 350116； 2. 福建省锅炉压力容器检验研究院， 福建 福州 350008)

针对生产实际中无法对燃煤组分进行在线检测分析的问题， 建立了基于最小二乘支持向量机的燃煤的碳含量预测模型. 以工业锅炉燃煤的相关工业分析数据作为模型的输入， 并采用蚁群算法对最小二乘支持向量机相关参数进行寻优以提高模型的建模精度. 应用该模型对福建地区工业锅炉燃煤的碳元素含量进行预测， 预测结果的最大误差为1.18%， 平均误差为0.64%. 和传统多元逐步回归预测方法相比， 该预测模型具有较高的预测精度， 为工业锅炉二氧化碳排放量的科学计算奠定了基础.

锅炉； CO2排放量； 最小二乘支持向量机； 碳元素含量

0 引言

二氧化碳是导致温室效应的主要气体. 据统计， 自1986年起， 我国煤炭燃烧产生的CO2排放量， 占所有碳排放总量的40%左右[1]. 工业锅炉的燃料以煤炭为主， 燃料的不完全燃烧， 致使其热效率水平低下， CO2排放量大幅上升， 造成了严重的能源浪费和环境污染. 因此， 准确实时地测算锅炉的碳排放量， 不仅有助于锅炉用户建立煤耗损失的概念， 也为评价锅炉运行的经济性和安全性提供依据.

在计算燃煤设备碳排放量时， 人们采用了碳排放系数， 其原理是根据煤耗量乘以相应的系数从而得到碳排放量的值， 如国家发改委制定的锅炉碳排放系数为0.67. 具体计算时， 还应考虑锅炉的类型和燃煤品种进行相应的修正. 文献[2]给出的碳排放估算公式考虑了不同燃烧用煤的品种特性， 但没有将排烟温度、 飞灰含碳量等影响热效率的重要参数引入式中； 文献[3]给出的CO2排放量计算方法， 未就公式中有关参数的来源进行明确阐述， 如煤的含碳量、 热效率和固体未完全燃烧损失等， 因而在具体应用时存在较大的局限性； 文献[4]在推导CO2排放量计算方法时， 固体未完全燃烧损失仅与入炉煤质有关， 未考虑锅炉的实际运行工况， 该方法计算所需的烟气体积和空气体积也不易获取. 在前人工作的基础上， 本研究通过新的途径对碳排放计算方法进行研究， 以期提高碳排放的计算精度.

在大多数CO2排放量的计算方法中， 煤的碳元素含量是一个重要参数. 但实际上， 大多数锅炉用户仅对入炉煤质进行工业分析以获得煤的发热量等值， 而较少分析煤的元素组成. 只有大型电站锅炉和煤矿公司才有条件对煤的元素组成进行试验分析. 该实验过程冗长， 操作繁杂， 微小的操作失误都可能导致分析数据的误差. 基于ACO-LSSVM软测量模型， 利用煤的工业分析值预测煤的干燥无灰基固定碳含量Cdaf， 通过换算公式计算得到收到基碳元素含量Car， 取得了较好的效果.

1 基于ACO-LSSVM的煤碳含量分析

1.1 最小二乘支持向量机(LSSVM)

支持向量机(SVM)是Suykens等[5]提出的一种机器学习方法， 而LSSVM则将样本误差的二范数作为损失函数， 代替了标准SVM使用的二次规划方法， 从而提高模型的鲁棒性能及泛化能力.

假设有n维非线性相关的向量构成的样本. 可以表示如下:

式中: 输入参数xi为煤的工业分析所得参数值； 参数yi作为它的输出. 通过非线性映射将样本集合映射到高维的Hibert空间φ(xi). 构造出最优决策函数：

它满足约束条件：

通过构造Lagrange泛函：

再根据优化条件， 函数L(·)对各变量的偏导数为零， 利用核函数K(x,xi)取代高维映射空间中复杂的点积运算. 最终转化为求解方程：

最后得到的拟合公式为：

1.2 蚁群优化算法(ACO)

蚁群算法最早由Dorigo和Collrni在1991年提出. 许多学者以旅行商问题(TSP)为基本问题， 与其他的常用启发性方法作了多方面的对比. 对若干典型的对称型和非对称型TSP问题， 先后采用了退火算法、 遗传算法、 神经网络等多种算法进行求解， 蚁群算法的结果好于一般算法[6-7]. 优化LSSVM模型的本质是应用蚁群算法处理连续优化问题， 从而找出最优的正规化参数和高斯核函数(γ，σ2)组合， 使得目标函数达到最小值. 优化步骤如下：

① 建立待优化的目标函数：

式中：yi为第i个样本的真实值；yfi为第i个样本的预测值. 设约束集为：γ∈(γmin，γmax)和σ∈(σmin，σmax).

② 确定蚂蚁数和最大迭代次数， 设定蚂蚁位置即(γ，σ2)的集合.

③ 计算出每个蚂蚁的信息素大小[8]:

式中为避免信息素趋近于0，f(x)应进行修正.

④ 根据信息素大小， 进行迭代计算， 求解最优蚂蚁位置， 最终获得最优参数(γ，σ2).

1.3 ACO-LSSVM建模步骤

工业分析得到的参数有灰分Ad、 挥发份Vdaf和固定碳FCad等， 不同基准下的各参数值通过换算公式计算得到. 固定碳FCad可通过公式FCad=100-Mad-Aad-Vad计算得到. 为提高预测精度， 拟将煤炭按照烟煤、 无烟煤、 褐煤和贫煤四种类型分别建模：

① 确定模型输入量, 输入变量xi为煤的水分、 灰分和挥发份；

② 优化模型参数, 按1.2节的步骤 ①～④ 对模型的参数进行优化选择； 优化过程设置： 蚁群规模为20， 最大迭代次数为100， 正规化参数γ∈[1, 512]， 高斯核函数σ∈[1, 512]；

③ 采用ACO优化后的模型参数， 建立LSSVM模型；

④ 输入新的变量， 由LSSVM模型计算， 获得碳含量预测值.

2 CO2排放量计算方法

在完全燃烧情况下， 1 kg的碳在标准状态下将产生体积为1.867 L的CO2. 少量不完全燃烧的碳反应生成的CO体积与等量的碳完全燃烧产生的CO2体积相当， 并且在大气中CO会进一步氧化成CO2， 因此将这部分CO按照完全燃烧反应进行计算. 由此， 煤燃烧生成的CO2体积可用公式(9)表示：

式中:CR为煤燃烧之后实际利用的碳含量(kg·h-1)，CR的计算如下：

式中:B为煤的消耗量(kg·h-1)；Car为煤的收到基碳含量， 可应用前述基于ACO-LSSVM的煤碳含量分析方法计算得到Cdaf， 进而得到Car.

上式中的Glz、Glm、Gfh和Gyd分别为单位时间内炉渣、 漏煤、 飞灰和烟道中灰分的质量(kg ·h-1)；Clz、Clm、Cfh和Cyd分别为其对应的可燃物的碳含量.

目前， 对于炉渣和飞灰量的大小， 都设有限定值， 但无法就其中的碳含量作明确规定， 大部分锅炉受条件限制未进行飞灰和炉渣含碳量分析. 在燃烧效率低下的情况下， 锅炉飞灰和炉渣的含碳量甚至高达15%(质量分数).

固体未完全燃烧热损失q4可按式(12)求得：

式中:Qnet为煤的低位发热量.

由公式(10)、 (11)和(12)得到：

CR=B(Car-Qnetq4/32

q4还可以从锅炉的反平衡热效率计算公式得到：

式中:q2为排烟热损失；q3为气体不完全燃烧损失；q5为散热损失；q6为灰渣物理热损失. 以工业锅炉为例， 式中η表示为：

式中:D为蒸汽流量；hs为蒸汽焓；hw为给水焓.

将公式(13)、 (14)和(15)代到公式(9)得到下列CO2排放量的计算公式：

式中，q2采用文献[10]的方法计算得到；q3和q5按常用方法处理. 计算q6所需要的炉渣份额， 在不具备实验条件时， 可以通过查询统计数据库获得， 或采用设计规定值. 结合前文分析， CO2排放量的计算流程如图1所示.

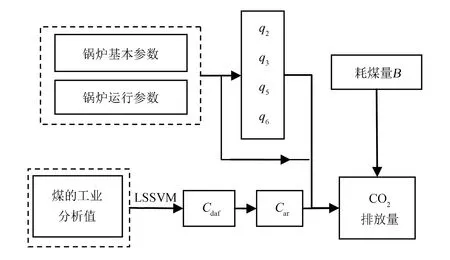
图1 CO2排放量计算流程图Fig.1 The flow chart of CO2 emissions calculation

3 实例分析

3.1 应用ACO-LSSVM的含碳量计算

采用120组无烟煤数据作为模型的输入， 通过ACO优化计算， 模型最优参数为γ=84.136，σ2=146.269， 由此建立ACO-LSSVM模型. 将该方法得到的数据结果与文献[9]采用的多元逐步回归(MRA)计算方法得到的数据进行对比， 两种方法的训练曲线如图2所示. 进一步应用训练得到的模型对福建地区部分煤矿煤的碳元素含量[10]进行预测， 计算结果如表1所示.

图2 两种方法的Car训练过程实际值与计算值曲线对比Fig.2 The contrast curve of the actual value and predicted value of the two Car training methods

表1 福建地区煤的碳元素含量预测情况

Tab.1 Predicted results of coal’Cdafin Fujian province

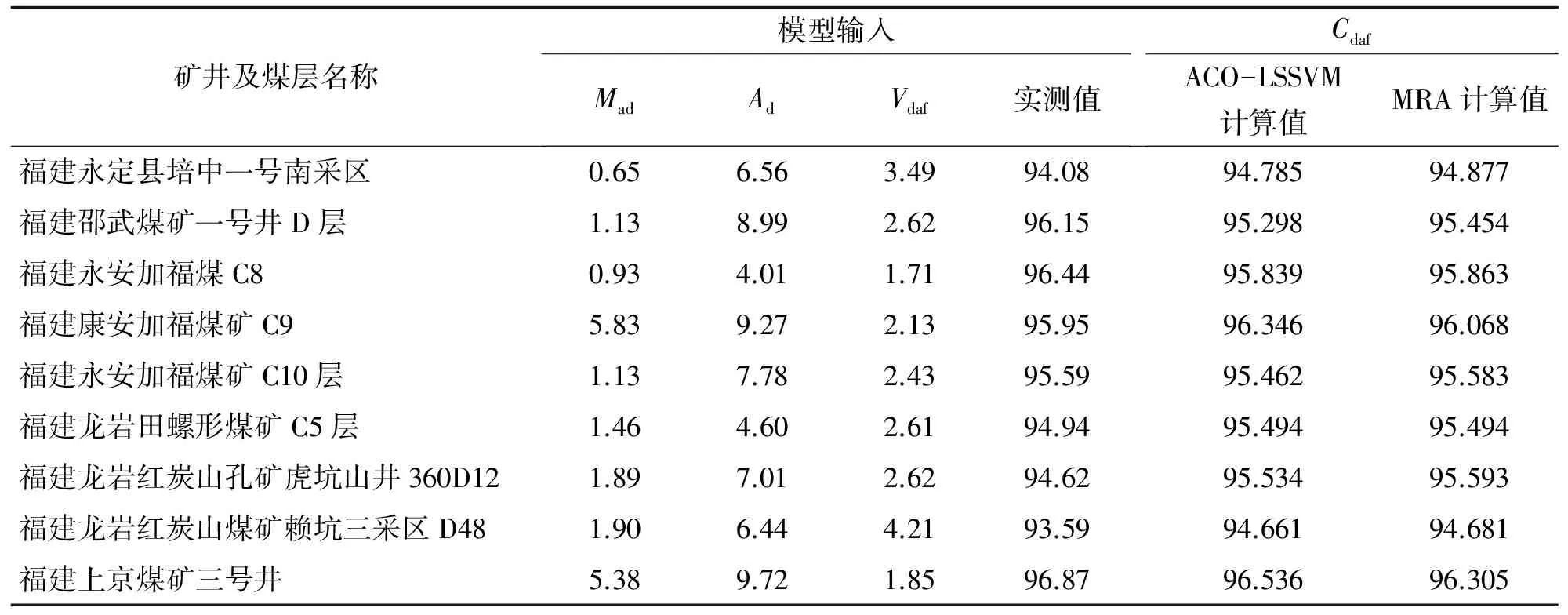
矿井及煤层名称模型输入MadAdVdaf实测值CdafACO-LSSVM计算值MRA计算值福建永定县培中一号南采区0．656．563．4994．0894．78594．877福建邵武煤矿一号井D层1．138．992．6296．1595．29895．454福建永安加福煤C80．934．011．7196．4495．83995．863福建康安加福煤矿C95．839．272．1395．9596．34696．068福建永安加福煤矿C10层1．137．782．4395．5995．46295．583福建龙岩田螺形煤矿C5层1．464．602．6194．9495．49495．494福建龙岩红炭山孔矿虎坑山井360D121．897．012．6294．6295．53495．593福建龙岩红炭山煤矿赖坑三采区D481．906．444．2193．5994．66194．681福建上京煤矿三号井5．389．721．8596．8796．53696．305

分别采用RSME、 MPE和MNE这3个误差指标， 对比这两种方法的性能， 结果见表2.

平方根误差:

最大误差：

最小误差：

表2 两种方法性能指标对比

由表2可知, 经过蚁群算法优化参数的LSSVM模型得出的煤质Cdaf值具有较高的精度. 其最大误差为1.18%， 平均误差为0.64%.

3.2 CO2排放量计算

以一台型号为SHL10-1.57-WII的工业锅炉为例进行碳排放量计算. 该锅炉蒸汽平均温度为160.4 ℃， 给水平均温度为41.2 ℃， 燃用福建永安加福无烟煤， 煤的工业分析数据为Mad=0.65%(以下均为质量分数)、Ad=6.56%、Vdaf=3.49%， 煤的发热量Qnet=33 185 J·g-1. 应用前文的ACO-LSSVM方法计算得到Cdaf=94.785%， 气体不完全燃烧损失q3取为0.8%， 额定状态下的散热损失q5取为1.7%， 灰渣物理热损失q6取设计值为0.5%. 得到简化的碳排放量计算公式， 如下式所示.

将在线采集的8个小时段的锅炉运行参数数据， 包括给煤量、 烟气含氧量、 排烟温度、 蒸汽流量等代入上式， 其中， 对q2的计算采用文献[11] 的方法. 得到该锅炉的碳排放量， 具体结果见表3.

通过以上锅炉碳排放量计算模型， 利用煤的工业分析数据和在线采集的锅炉运行参数， 计算得到的碳排放量具有较高的精度和计算速度. 为计算锅炉的碳排放提供了一种新的方法途径.

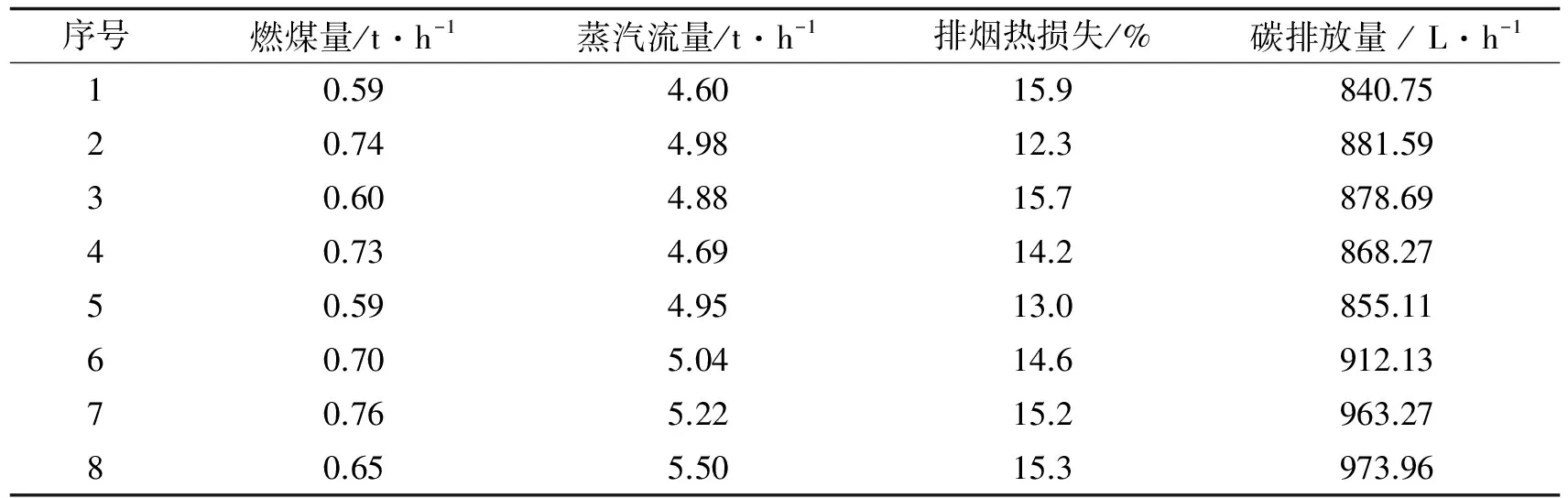
表3 8个小时段锅炉碳排放量计算结果

4 结论

1) 提出的ACO-LSSVM方法， 通过煤的工业分析值预测出含碳量， 较MRA方法有效地降低RSME值， 提高了预测精度.

2) 以输入参数的获取作为推导的突破点， 获得了较为准确的CO2排放量计算模型. 该公式可方便地应用于锅炉在线监测系统， 将锅炉节能减排工作带入一个新的高度.

3) 蚁群算法优化最小二乘支持向量机的最优参数组合： 正规化参数γ=84.136， 高斯核函数σ2=146.269.

4) 通过对输入参数进行相应的调整， 即可将模型应用于不同类型的锅炉.

[1] 中华人民共和国国家统计局. 中国能源统计年鉴[J]． 北京： 中国统计局出版社, 2011．

[2] 李静波, 樊石磊. 火电厂脱硫技术浅析[J]. 内蒙古环境科学, 2010, 22(4):19-24.

[3] 梅国栋， 韩瑞国． 锅炉二氧化碳排放量的计算及其减少途径[J]. 城市环境与城市生态， 2000， 13(4)： 52-54．

[4] 房靖华， 赵玉兰， 曾涛方． 燃煤锅炉的CO2排放计算和讨论[J]． 煤炭转化， 1999， 22(1)： 63-64．

[5] Johan A K Suykens. Nonlinear modeling and support vector machines[C]//Proceedings of the 18th IEEE Instrumentation and Measurement Technology Conference. Budspest: [s.n.]， 2001: 287-294.

[6] 马良， 朱刚， 宁爱冰． 蚁群优化算法[M]． 北京： 科学出版社， 2008．

[7] 董改芳, 付学良. 蚁群优化算法的研究与改进[J]. 内蒙古农业大学学报： 自然科学版, 2012, 33(2): 185-188.

[8] 马卫 ， 朱庆保． 求解函数优化问题的快速连续蚁群算法[J]． 电子学报， 2008， 36(11)： 2 120-2 124．

[9] 李太兴， 张婷， 刘振刚． 基于MATLAB的煤质元素分析通用计算模型研究[J]．锅炉技术， 2007， 38(5)： 22-24．

[10] 陈鹏． 中国煤炭性质、 分类和利用[M]． 北京： 化学工业出版社， 2001．

[11] 李智， 蔡九菊， 曹福毅, 等. 电站锅炉效率在线计算方法[J]． 节能， 2005(3)： 28-29．

(责任编辑： 洪江星)

Calculation of CO2emissions in boilers based on ACO-LSSVM method for carbon element analysis of coal

XU Qiaoling1, WANG Yanduan1， LIN Weihao2, LIANG Hang2, WAN Jin1

(1. College of Chemical Engineering, Fuzhou University, Fuzhou, Fujian 350116, China;2. Fujian Province Special Equipment Inspection Institute, Fuzhou, Fujian 350008, China)

The carbon content of coal is one of the important parameters in calculating emissions of carbon dioxide in industrial coal boilers, but it is difficult to be measured quickly or accurately during the boilers operation. Based on the element analysis of coal from laboratory, a LSSVM (least-squares support vector machine) model for predicting the carbon content of coal is developed. Ant colony algorithm optimization is used to optimize the parameters in LSSVM in order to improve the accuracy of the model. Propose predictive model is applied to predict the carbon content of coal that comes from Fujian region, the maximum error and average error of the prediction results are 1.18% and 0.64%， respectively. Comparing proposed method with multivariate stepwise regression method, the results show that this method has higher simulation accuracy. This carbon element analysis model provides solid basis for calculating emissions of carbon dioxide in industrial boilers.

boiler； CO2emissions； least square support vector machine； carbon content

10.7631/issn.1000-2243.2015.04.0548

1000-2243(2015)04-0548-06

2014-05-29

许巧玲(1956-), 教授， 主要从事工业过程控制及节能技术研究, zhhqxu@fzu.edu.cn

国家自然科学基金资助项目(60804027; 61374133); 福建省质量技术监督局科研专项资助项目(FJQI201212)

TK314

A