复杂产品设计决策中耦合因素处理的简便方法

李廖平， 陈 亮， 肖品辉

(福州大学机械工程及自动化学院， 福建 福州 350116)

复杂产品设计决策中耦合因素处理的简便方法

李廖平， 陈 亮， 肖品辉

(福州大学机械工程及自动化学院， 福建 福州 350116)

对复杂产品设计决策中耦合因素进行分析， 并利用已有的响应面法对耦合因素进行处理. 鉴于理想响应面的建立需要大量计算与迭代， 而且精度受拟合函数影响， 给出一种基于鲁棒思想的耦合因素处理方法. 其既可有效降低学科间的相互影响和耦合程度， 又可保证满意的设计决策结果， 计算简便. 最后以汽车盘式制动器的设计决策为例进行分析， 并将两种方法的结果进行对比， 表明了本文方法的可行性和有效性.

耦合； 多学科设计； 鲁棒设计； 设计决策； 盘式制动器

0 引言

随着科学技术的迅猛发展和市场竞争的不断加剧， 对工业产品的功能和性能提出了更高的要求， 从而增加了产品的复杂性. 而复杂产品的设计往往涉及多个学科领域， 需要综合考虑多学科彼此间的相互作用和协同效应， 进行协同设计决策来获得各方满意的设计方案. 因而， 复杂产品设计中存在着复杂的学科耦合关系， 学科间相互制约， 甚至存在矛盾冲突， 这使得最终设计方案的确定十分困难. 因此， 如何有效地处理学科间的耦合关系， 获得各学科均满意的设计解是复杂产品开发的核心问题之一.

对耦合因素的处理， 目前较为普遍的方式是利用试验设计的方法构建各个学科间的理想响应面(best reply correspondence, BRC)来对其他学科的设计决策进行预测和分析. Lewis等[1]结合飞行器中的多学科设计问题从合作、 非合作、 领导随从三种博弈情形进行一系列的探讨， 分别建立了相对应的博弈模型， 给出基于理性响应面的决策方法, 并结合相容决策支持问题(decision support problem, DSP)进行设计决策. Xiao[2]将博弈理论和设计能力指数相结合来指导多学科间的决策问题. Liang等[3]运用博弈理论对非合作的多学科问题进行研究， 并结合该方法运用到船舶舱室布局的设计中， 取得较理想的结果. Habbal等[4]运用纳什博弈对多学科设计进行求解， 并将此运用到热传递系统的设计中. 闫利军等[5]运用纳什博弈对非合作的多学科耦合问题进行建模， 提出一种协同决策方法， 利用一致性区间算法和设计性能指标对响应面技术进行改进.

本文基于对复杂产品设计中耦合特点的分析， 针对响应面法对耦合因素进行处理时， 能较好地解决复杂产品设计中的耦合问题， 但是理想响应面的建立需要大量的计算与迭代， 且精度受拟合函数影响. 为了减少设计过程中的计算成本以及拟合函数的精度对设计决策影响， 给出了一种基于鲁棒思想的耦合因素处理方法. 其计算简便， 可以有效降低学科间的相互干扰， 又可保证满意的设计结果. 最后, 以汽车盘式制动器设计为例， 对该方法的可行性和有效性进行了验证.

1 复杂产品设计决策中耦合因素分析

图1 复杂产品耦合系统Fig.1 Coupling systems of complex products

与传统的设计方法相比， 复杂产品设计决策的核心问题之一是学科间的耦合处理. 由于目前产品开发大都涉及到多个学科多个领域， 学科间相互交叉耦合， 这就大大增加了产品开发的困难. 涉及的学科越多， 耦合关系越复杂， 产品开发的成功率就越低. 一个简单复杂产品耦合系统如图1所示. 其中:X是设计变量；Y是耦合变量，Yij表示学科i对学科j的耦合变量；f是设计目标；g，h分别为不等式约束和等式约束.

在实际开发中， 由于地域、 学科的专业性以及资源共享上的障碍等原因， 各个学科的设计人员之间的信息交流存在障碍， 设计人员不得不在信息不确定的情况下进行设计决策. 各个学科根据自身的情况做出符合本学科满意的设计决策， 但同时学科的设计决策又对其他学科的设计决策产生影响.

2 耦合因素处理的响应面法

针对复杂产品的耦合问题较为普遍的处理方法是利用设计变量之间的相关性构建学科间的理想响应面(BRC). 通过理想响应面进行求解， 得出在满足各个学科设计期望基础上的较为理性的设计决策[2].

BRC的方法是通过穷举他方策略， 然后根据他方策略相应地制定自身策略的一个过程. 然而在实际产品设计中， 策略的穷举是无法实现的. 因此, 只能通过抽样的方法从无穷的策略中进行有限的选取， 并根据选取的策略来确定自身的策略， 然后对这些策略组合进行统计与分析， 这实质上是一个试验设计的过程. 此后， 通过对试验设计得到的大量数据进行分析， 就可以构建变量之间的相关关系， 拟合出变量间的函数表达式， 以此来构建一个近似的BRC.

假设Xi代表着隶属于第i个学科的设计变量， 而其它学科的耦合变量集统一表示为Yi以方便后续步骤的描述. BRC构建方法如下： 1) 对学科i， 寻找学科i所需的其他学科的设计变量Yi. 2) 对其他学科的设计变量Yi建立试验设计. 3) 对其他学科的设计变量Yi和学科i的设计变量Xi建立响应面模型. 4) 寻找BRC的交集作为多学科的非合作的均衡解.

BRC技术虽然是一种解决学科间耦合的有效方法， 但是在实际应用中存在2个不能忽视的缺点： 一是计算量大. 进行试验设计以及构建响应面需要大量的计算量， 使原本简单的问题复杂化. 二是精度受拟合函数影响.BRC的构建是通过对试验设计进行大量数据分析， 得到变量之间的相关关系， 拟合出变量Xi与Yi之间的函数表达式. 设计结果受到拟合精度的影响， 若拟合精度不理想， 有可能得到不合理的结果.

3 耦合因素处理的鲁棒方法

3.1 鲁棒设计

鲁棒设计是使产品的性能对外界干扰不敏感， 并使产品在其寿命周期内都能持续满意地工作的一种设计方法[6]. 鲁棒设计有两个目标： 一是使产品目标函数尽可能达到期望值； 二是使由于各种干扰因素引起的目标函数的波动尽可能小. 在鲁棒设计中， 将影响目标函数的因素分为两类： 可控因素与噪声因素. 可控因素是设计人员可以严格控制的因素， 在鲁棒设计中要求设计师选出这些因素的最佳取值， 以达到改进产品目标函数的目的； 而噪声因素或称为不可控因素则是对设计有影响且难以控制的因素， 它是造成产品质量特性变差的原因.

采用望小的优化模型， 因此目标函数的期望值一般为0或者最小值fmin， 鲁棒设计的数学模型如下：

3.2 耦合因素的鲁棒设计法

通过计算设计变量对各个学科的影响因子， 并对该影响因子进行模糊聚类， 根据设计变量与学科的相关性进行聚类划分. 通过聚类分析， 将设计变量分配给与之关系较为密切的各个学科， 则设计变量为各个学科的可控变量. 若设计变量是耦合变量, 同时影响多个学科的目标函数时， 则设计变量相对于与之关系较为密切的学科为可控变量， 而对于其他学科则为噪声变量. 通过此种方法将设计变量进行分配以达到解耦的目的， 降低了多学科耦合系统的复杂程度， 为解决较为复杂的耦合问题提供了一种思路.

鲁棒设计的基本原则是提高产品质量的同时减少设计、 生产以及使用过程中产生的偏差对产品质量的影响. 基于此种思想， 在多学科耦合问题中， 各个学科只需在各自的学科内降低噪声因素对目标函数的影响， 同时设计决策时只考虑可控因素对学科的影响， 则可以尽可能地减少其他学科对本学科的影响， 使自身学科获得较为满意的设计决策.

以图1为例， 学科1和学科2相互耦合， 学科1的可控因素为X1， 学科2的可控因素为X2. 由于学科1和学科2相互耦合， 则学科1的噪声变量为由学科2控制的Y21. 反之亦然， 学科2的噪声变量为学科1控制的Y12.

为了便于计算， 利用一阶泰勒展开对约束函数的偏差做近似处理：

由于变量X、Y分别为可控变量和噪声变量， 两者相互独立. 根据概率论的有关知识， 复杂产品耦合问题进行鲁棒处理后的目标方差可表示为：

通过此种方法可以降低学科间的耦合程度， 各个学科间的相互干涉情况被削弱， 同时学科对可控因素进行控制保证了学科自身的设计目标. 最终的设计决策有可能不是最好的， 但是却能在尽可能低的计算成本下让各个学科都满意.

在复杂产品耦合因素的鲁棒处理中， 优化目标有两个： 目标函数尽可能达到期望值与噪声变量的方差σ2尽可能最小. 因此， 鲁棒设计是双目标优化问题. 在鲁棒设计中， 目标函数f与方差σ2表示意义不同. 前者表示对产品性能的要求， 而方差σ2表示产品性能的稳健程度， 并且目标函数f与方差σ2的量纲大小一般不同. 因此， 本文认为统一目标函数法不能很好地表示目标函数f与方差σ2之间的关系. 针对上述问题， 对鲁棒设计的双目标问题采用字典排序的方式进行处理. 字典排序是一种表示偏好的方法. 假设有n个目标fi， 将n个目标fi按照字典排序的方式进行排列， 依次进行求解. 即将方差σ2设置为第一级， 目标函数f设置为第二级. 具体方法是： 先对方差σ2进行求解， 确定出部分设计变量值， 再对目标函数f进行计算求出剩下的解. [Y21L,Y21U]耦合因素处理的鲁棒设计模型如图2所示.

对学科1来说， 在知道噪声变量Y21的范围但不知道学科2会如何设计时， 学科1将噪声变量Y21看作不确定因素， 运用鲁棒设计， 使得Y21对学科1的目标函数性能波动的影响最小作为第一级目标， 目标函数尽可能达到期望值作为第二级目标. 这样则可以减轻Y21对学科1设计影响， 使得学科1对学科2的设计决策具有鲁棒性. 同理， 学科2也按照鲁棒设计进行设计则可以减轻学科1对其的影响. 通过此种方式学科进行设计决策时能对其他学科的不确定影响具有鲁棒性.

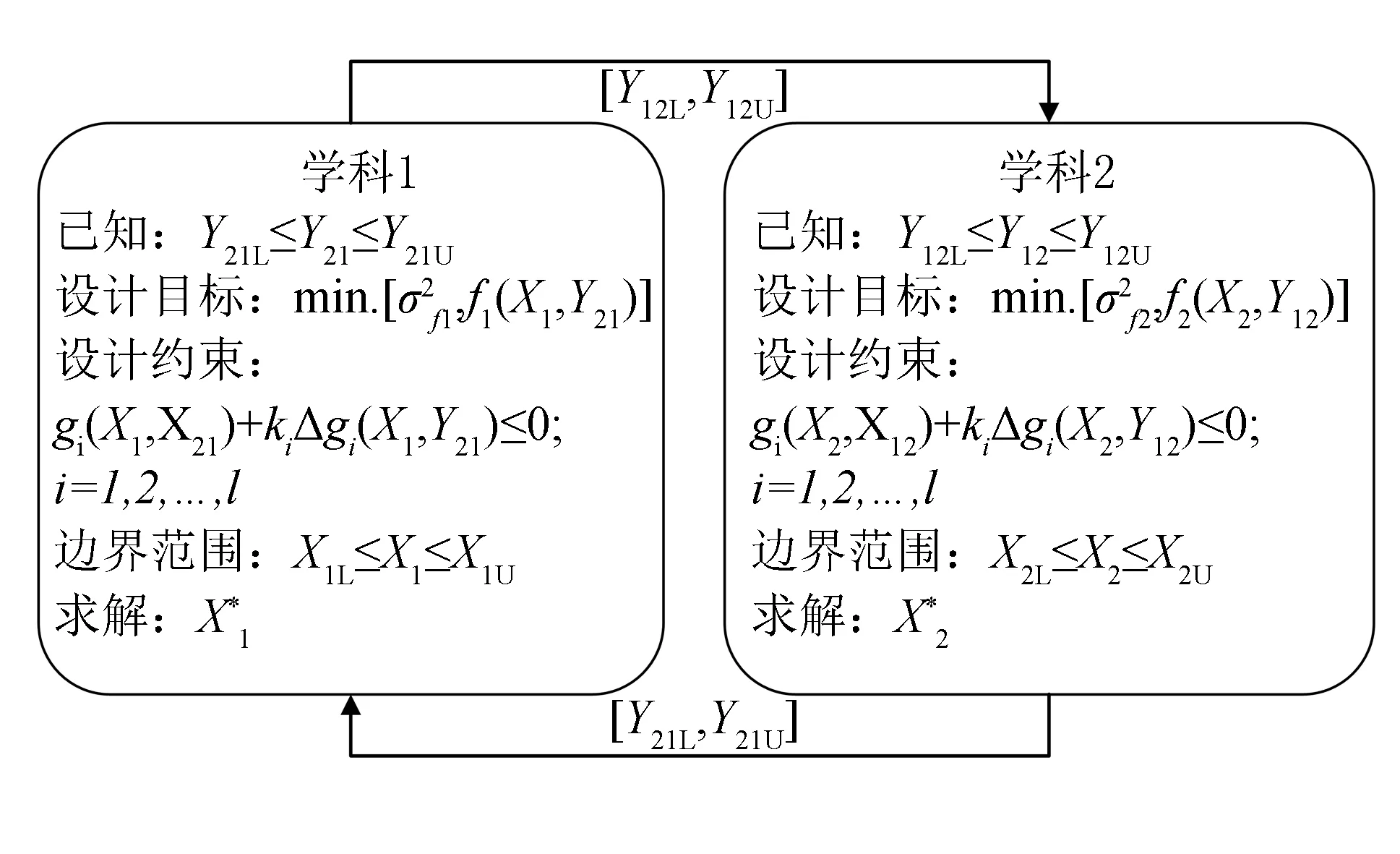
图2 多学科耦合系统的鲁棒处理模型 Fig.2 Robust processing model of multidisciplinary coupling systems

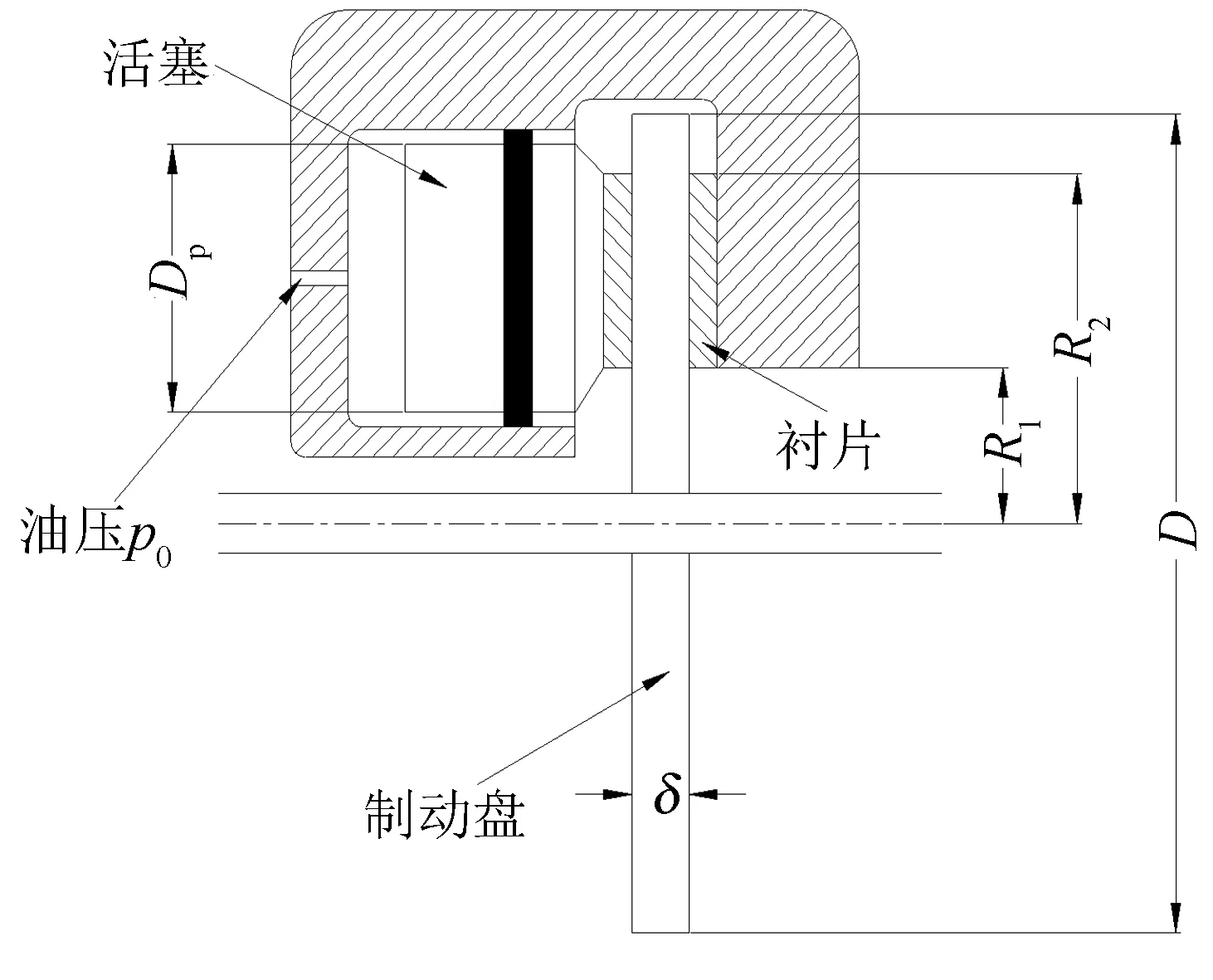
图3 浮钳盘式制动器的结构图 Fig.3 Structure of floating caliper disc brake

4 实例分析和比较

4.1 实例分析

设计如图3所示， 以汽车盘式制动器为例进行验证. 已知单个车轮承载质量W1=4 101 N， 制动初始速度v0=100 km·h-1， 制动初始角速度ω0=88.46 s-1， 轮胎滚动半径Rb=314 mm ， 制动盘最大直径Dmax=300 mm， 制动盘内径Dh=65 mm， 制动片和制动盘间的摩擦系数β=0.38， 车轮和路面间摩擦系数φ=1， 衬垫允许最大压力[qmax]=3.5 MPa， 油缸允许最大油压[pmax]=7 MPa， 油缸厚度τc=5 mm， 重力加速度为g， 制动衬片的密度为ρp=2 595 kg·m-3, 热工当量J=1 N·m·J-1, 油缸的中心在制动片的平均半径处的距离d=5 mm， 附着系数φ=1， 制动片不应与轮毂发生干涉的临界直径Dh=65， 制动盘的比热容为c=419 J·(kg·K)-1. 主要设计变量包括摩擦片内径R1， 摩擦片外径R2， 活塞直径Dp， 制动盘的1/2厚度δ， 摩擦片半角θ， 油压p0， 制动盘直径D， 各变量范围为70≤R1≤100， 100≤R2≤130， 40≤Dp≤70 ， 10≤δ≤20， 25≤θ≤45 ， 4≤p0≤7, 100≤D≤300. 制动器设计涉及三个学科： 运动学、 结构设计、 热力学. 其目标函数和约束条件分别见表1和表2.

表1 目标函数

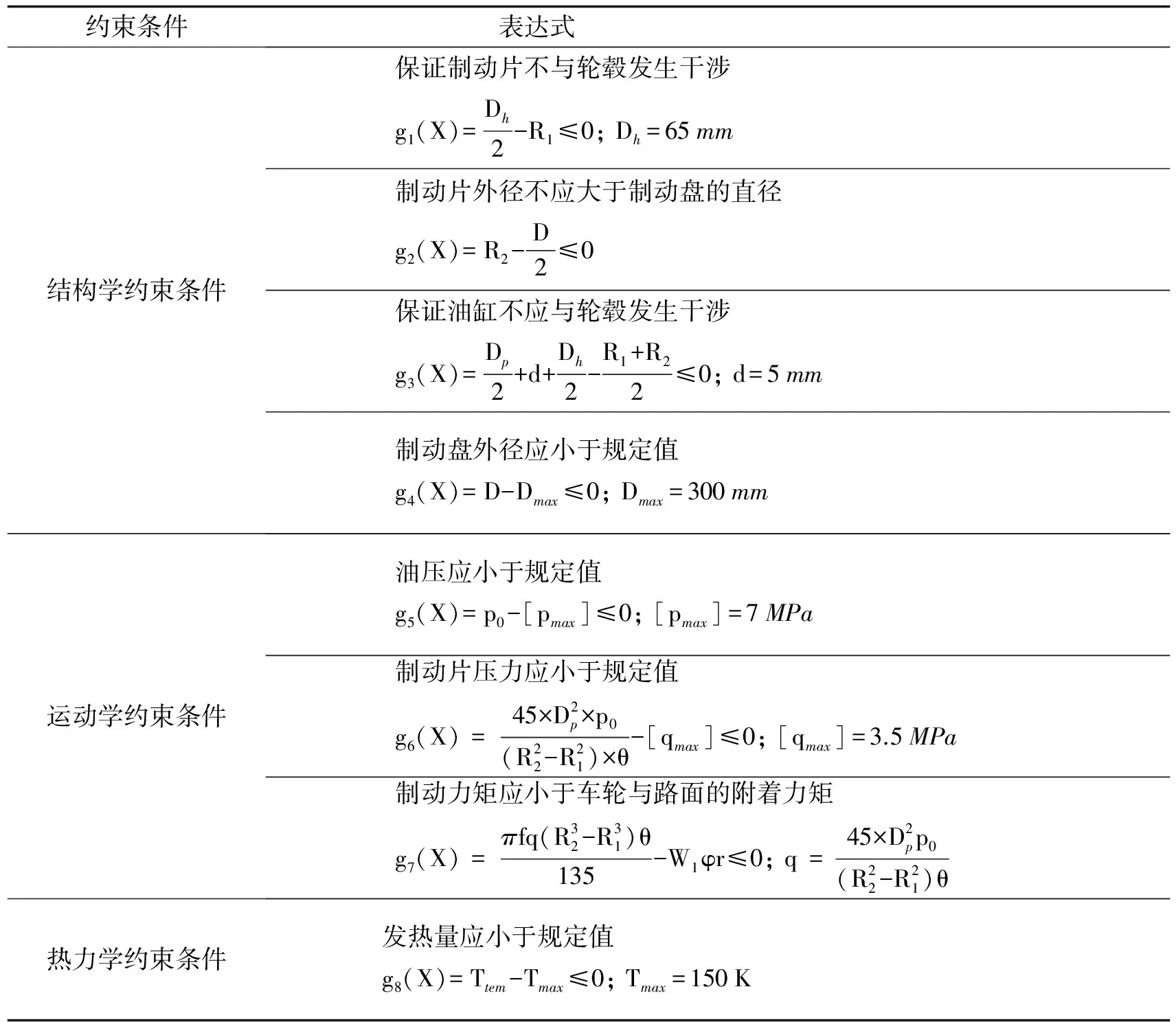
表2 约束条件

4.2 基于鲁棒思想的处理方法

图4 制动器多学科关系模型Fig.4 Multidisciplinary relation model of brakes

制动器设计涉及三个学科： 运动学(t)、 结构设计(m)、 热力学(T). 利用模糊聚类方法将设计变量划分给三个学科作为其可控因素.

运动学学科： 摩擦片内径(R1)， 摩擦片外径(R2)， 活塞直径(Dp)和油压(p0). 结构设计： 制动盘的1/2厚度(δ)和摩擦片半角(θ). 热力学学科： 制动盘直径(D). 利用前文的设计决策方法， 三个学科各自进行设计决策， 如图4所示.

1) 运动学学科进行设计决策. 对可控因素R1,R2,Dp,p0进行设计决策， 结果为R1=77.973 3，R2=124.963 3,Dp=61.784 6,p0=5.471 8.

2) 结构设计进行设计决策. 可控因素δ和θ. 热力学科控制的可控因素D对于结构设计学科是噪声因素， 因此结构设计学科的设计决策的目标有两个： 质量对噪声因素D的方差最小和质量m的最小. 先对方差进行求解， 得δ=10， 由运动学学科设计决策知R1=77.973 3，R2=124.963 3， 对质量进行求解得θ=25， 所以设计决策结果为δ=10,θ=25.

3) 热力学科进行设计决策. 可控因素D. 结构设计控制的可控因素δ对于热力学科是噪声因素， 因此热力学科的设计决策的目标有两个： 最高温度对噪声因素δ的方差最小和最高温度T的最小， 设计决策结果D=300.

综合上述结果， 可得三个学科的目标函数为t=2.836 9,m=2.587 8,T=79.183 9.

4.3 理想响应面法

令R1，R2，Dp，d,q,P0,D分别为x1,x2,x3,x4,x5,x6,x7.

1) 运动学科t理想响应面BRC1的建立. 由于运动学科t只与自身变量x1,x2,x3,x6相关， 而与其他策略方所控制的变量无关， 故对其进行优化求得的x1,x2,x3,x6即为该博弈方的理想响应面， 其结果为：

2) 结构设计m理想响应面BRC2的建立. 选取中心复合点试验方法进行数据的采集， 根据试验结果， 以二次多项式为拟合方程， 并运用Matlab进行非线性拟合， 得m的最终理想响应面为：

x5=26.267 81+0.065 616x1-0.076 036x2+0.221 57x3+0.609 93x6-0.020

3) 热力学T理想响应面BRC3的建立. 观察T的表达式可知， 其与变量x4和x7相关， 只需要针对x4进行试验设计即可， 由于T是关于x7的单调递减函数， 因此T的响应面为：

对三方的理想响应面求交得：

x1=78.030 3，x2=125.037 2，x3=62.348 8，x4=10.298 2，x5=32.749 9，x6=5.373 2，x7=300

观察上述变量可知， 其均处于各自的取值范围内， 将求得的非合作解带入各约束条件中进行校验， 得出该非合作解是一组可行解， 其求得的各目标函数值为：t=2.832 9，m=2.709 7，T=76.857 4.

可见， 得到的结果与理想响应面法得到的结果十分接近， 由此可说明本文方法的有效性.

5 结语

借用鲁棒思想对复杂产品的耦合问题进行设计决策， 其原理是通过减少噪声因素对学科的影响， 从而使学科性能稳定且符合设计要求. 而理想响应面法则是通过对其他学科设计决策的预测， 利用试验设计的手段列出设计因素之间的相关性， 从而得到复杂产品的设计决策. 虽然两种方法的原理、 手段不同， 但是其设计的出发点相同， 均是为了得到在不确定环境下复杂产品设计决策结果， 通过例子验证了方法的有效性. 本文方法最大的优点是克服了理想响应面法计算量大且受拟合函数精度影响的缺点. 在产品开发初期， 能在不投入大量计算时间与资金的前提下得到较为合适的设计决策.

[1] Lewis K, Mistree F. Modeling interactions in multidisciplinary design: a game theoretic approach[J]. AIAA Journal, 1997, 35(8): 1 387-1 392.

[2] Xiao A. Collaborative multidisciplinary decision making in a distributed environment[D]. Atlanta: Georgia Institute of Technology, 2003.

[3] Liang Z X, Yan L, Shang J Z. Ship cabin layout design using game theory[J]. Journal of Marine Science and Technology, 2008, 13(4): 446-454.

[4] Habbal A, Petersson J, Thellner M. Multidisciplinary topology optimization solved as a nash game[J]. International Journal for Numerical Methods in Engineering, 2004, 61(7): 949-963.

[5] 闫利军, 李宗斌, 袁小阳, 等. 鲁棒的多学科设计协同决策方法[J]. 机械工程学报, 2010, 46(5): 168-176.

[6] 崔玉莲, 吴纬. 鲁棒设计综述[J]. 质量与可靠性, 2010(4): 10-13.

(编辑： 蒋培玉)

The simple method to deal with the coupling factors in complex product design

LI Liaoping, CHEN Liang, XIAO Pinhui

(School of Mechanical Engineering and Automation, Fuzhou University, Fuzhou, Fujian 350116, China)

Analyzes the coupling factors in the complex product design decisions， using the existing response surface method to deal with coupling factors. In view of the establishing of ideal response surface needs a large number of calculation and iteration, and the accuracy are influenced by fitting function, a simple and effective method to process coupling factors based on robust ideas is given, which not only can effectively reduce the mutual influence and the coupling degree between disciplines, but also can ensure the satisfying results of design decisions. Finally, a car disc brake design decisions is given as an example, which shows the feasibility and effectiveness of the method presented in this paper by comparing the results of two methods.

coupling; multidisciplinary design; robust design; design decision; cisc brake

10.7631/issn.1000-2243.2015.04.0506

1000-2243(2015)04-0506-06

2014-10-13

陈亮(1963-), 教授, 主要从事现代设计理论与方法、 CADCAE和制造业信息化等研究, chenliang@fzu.edu.cn

国家自然科学基金资助项目(50875049)； 福建省自然科学基金资助项目(2014J01184)

TH122

A