一类二维分数阶偏微分方程解的适定性
苏延辉
(福州大学数学与计算机科学学院, 福建 福州 350116)
一类二维分数阶偏微分方程解的适定性
苏延辉
(福州大学数学与计算机科学学院, 福建 福州 350116)
研究一类二维分数阶偏微分方程的边值问题, 主要包括两方面内容: 一是研究了合适的分数阶Sobolev 空间及分数阶算子的性质; 二是发展了一个弱解的理论框架, 并建立了弱解的适定性理论. 这是构造数值方法(如有限元和谱方法等)求解二维分数阶偏微分方程的理论基础.
分数阶导数; 弱解; 变分形式; 适定性
0 引言
分数阶偏微分方程在现代科学中发挥着越来越重要的作用. 现代的研究表明, 很多重要的物理和生物系统均可以由分数阶偏微分方程来描述. 近年来出现大量的关于分数阶偏微分方程的理论分析和数值研究[1-6]. 但相对于整数阶方程的研究, 分数阶方程的研究是相当不完备的. 分数阶偏微分方程的主要困难在于: 1)分数阶算子是非局部算子; 2)分数阶算子F的伴随算子不是-F.
在文献[1-2]中, Ervin和Roop研究了分数阶导数空间并在有界区间和有界凸区域情形对稳态分数阶扩散方程的变分解提出了一个理论框架. 然而, 他们没有研究弱解的适定性. 在文献[3-4]中, Li和Xu研究了定义在有界区间上的分数阶Sobolev空间并对时空分数阶方程提出了弱解策略, 并证明了弱解的适定性. 更进一步, 他们针对弱解策略提出了数值计算的谱方法并进行了误差分析.
基于上述工作, 本文考虑二维凸区域上的分数阶空间, 主要包括两方面内容: 一是研究分数阶算子的性质, 发展一类分数阶偏微分方程变分解的理论框架. 二是证明弱解的存在性、 唯一性和适定性, 这是构造数值方法(例如有限元法和谱方法等)的理论基础.
1 问题及函数空间
1.1 基本定义
用Ω表示R2中光滑的有界凸区域, 用O表示一个区域, 它或者表示Ω或者表示R2. 在没有混淆的前提下, 符号O,Ω或R2略去不写. 设c为独立于任何函数的正常数, 令A 定义1 设v∈R2为单位向量, 则存在唯一的θ∈[0, 2π) 使得v=(cosθ, sinθ)∈R2. 设u(x,y)为R2上的函数, 其分数阶积分定义为: 设n-1≤s 这里Γ(·)为Gamma函数. 设n-1≤s 1.2 问题与预备引理 在讨论适定性之前, 首先引入一些有用的空间并建立这些空间的相关性质. 令 引理1 设Ω′,Ω如上, 对任意s∈(0, 1),u∈Hs(Ω), 则 证毕. 可以证明上述线性泛函是连续的. 利用以上引理, 可以证明如下基本结果。 由式(2), {vn}为L2(O)中的Cauchy列, 从而∃v∈L2(O)使得 一方面, 对μ-几乎处处的θ∈[0, 2π), 有: 另一方面, 由引理3及式(3), 有: 从而得到 利用定理1, 文献[4]中的相关引理作如下推广: 从而式(9)成立. 证毕. [1]ErvinVJ,RoopJP.Variationalformulationforthestationaryfractionaladvectiondispersionequation[J].NumerMethPDE, 2007, 22(2): 558-576. [2]ErvinVJ,RoopJP.VariationalsolutionoffractionaladvectiondispersionequationsonboundeddomainsinRd[J]. Numer Meth P D E, 2007, 23(2): 256-281. [3] Li X J, Xu C J. A space-time spectral method for the time fractional diffusion equation[J]. SIAM J Numer Anal, 2009, 47(3): 2 108-2 131. [4] Li X J, Xu C J. Existence and uniqueness of the weak solution of the space-time fractional diffusion equation and a spectral method approximation[J]. Commun Comput Phys, 2010, 8(5): 1 016-1 051. [5] Lin Y M, Xu C J. Finite difference/spectral approximation for the time fractional diffusion equations[J]. J Comput Phys, 2007, 225(2): 1 533-1 552. [6] Wyss W. The fractional diffusion equation [J]. J Math Phys, 1996, 27(11): 2 782-2 785. (编辑: 蒋培玉) Well-posedness of the 2D-fractional partial differential equations SU Yanhui (College of Mathematics and Computer Science, Fuzhou University, Fuzhou, Fujian 350116, China) We investigate the boundary value problem of two-dimensional fractional partial differential equations (FEPDEs). The main contributions of this work are twofold: first, we investigate suitable fractional Sobolev spaces for fractional partial differential equations and study the properties of the fractional operator. Then, we develop a theoretical framework of weak solutions and establish the well-posedness of the weak solutions. Consequently, this work provides the theory for constructing numerical method such as finite element method and spectral method for solving the fractional partial differential equations. fractional derivative; weak solution; variation formulation; well-posedness 10.7631/issn.1000-2243.2015.04.0435 1000-2243(2015)04-0435-05 2014-12-17 苏延辉(1981-), 讲师, 主要从事几何偏微分方程的研究,suyh@fzu.edu.cn 国家自然科学基金资助项目(11226081); 福建省自然科学基金资助项目(2013J05003) O241.8; O175.2 A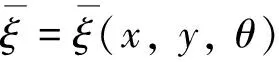
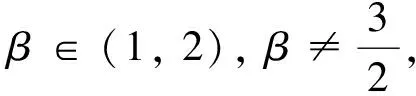

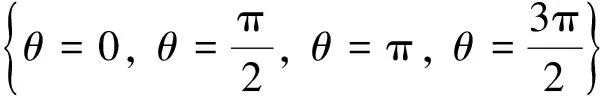


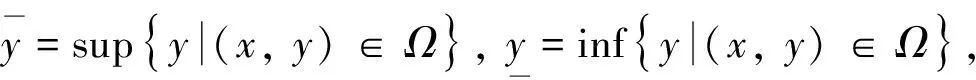






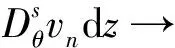







2 分数阶偏微分方程弱解的适定性




