当前估算教学：存在问题与解决策略

郑庆全

（1．齐鲁师范学院，山东 济南 250013；2．山东省基础教育课程研究中心，山东 济南 250013）

当前估算教学：存在问题与解决策略

郑庆全1，2

（1．齐鲁师范学院，山东 济南 250013；2．山东省基础教育课程研究中心，山东 济南 250013）

当前的估算教学引起了广泛关注，存在着诸多困惑．通过调查梳理出内容理解和教学认识方面存在如下问题：本体性内容的逻辑关系认识不明确、与其它内容之间的关系认识不清、应用条件认识不足、估算结果的科学评价标准不清楚、教和学的认识模糊，教学的阶段要求不明确．针对以上问题提出了“把握估算课程价值，确保育人价值实现；正确定位估算课程内容及其教学；坚持估算的特殊教学原则；把握估算课程内容特征，采取针对性的教学策略”的解决策略和“深入研读课标及其解读，把握课程的基本要求；整体梳理估算课程内容，有序逐步实现达标”的建议．

估算教学；问题；策略

自20世纪70年代以来，世界各发达国家开始把估算作为数学基本修养的一部分而引入中小学数学课程[1～2]．在国内，估算内容是在20世纪90年代以后的小学数学大纲和教材中首次作为选学内容引入的．在新一轮课程改革中的义务阶段数学课标实验版把估算作为必学内容，在2011年修订版中又进行了调整以进一步明确和清晰．在针对2011年课标修订版的山东省小学数学教师全员远程研修中，估算教学作为突出的困惑问题被广大教师提了出来，这里拟在对这些困惑初步梳理的基础上，明确存在的问题，进一步提出解决的策略建议．

1 当前估算教学中存在的问题

通过借助2012年山东省小学数学教师全员远程研修的网上在线平台调查了解到，估算教学在实践中存在着许多困惑．

1.1 现象描述

估算虽在小学数学课程内容中所占比重不大，但一线教师和学生存在的困惑却不少．比如，

（1）为了“估算”而“估算”．如教学中常要求学生估算“325+186≈、234-75≈”．感受必然是：教师在带着孩子“走教案”，让学生做什么学生就做什么，几乎没有体验与参与；学估算只是老师让学生估学生就估，只在课堂上有用． 由此，学生的估算学习必然是“教师让‘估’就‘估’，教师让精确计算就精确计算”，对“为什么要估算”“什么时候需要估算”，学生很茫然，他们体验不到“估算”的必要性，也不能正确选择何时估算何时精确计算．显然，这种“估算”教学的实际与课标的要求相去甚远．

（2）估算方法的多样化使教师不知如何评价．如262+173+208+145，262可估成300，也可估成200；145可估成150，也可估成100，所以估算结果莫衷一是．于是，“那么多的估算方法，到底哪个对啊？”这样的问题经常见到．

（3）仅把“估算”看作一种具体的技能教给学生．如，常让学生解决这样的问题：“电话机（148元）比自行车（350元）大约便宜多少元？”要求学生不能精确到百位，要精确到十位进行估算，以追求比较精确的结果．这样“估算的结果最接近精确数就是最好的估算吗？”的问题就出现了．

（4）如何表征估算成为困惑的问题．如，当估算以“解决问题”形式出现的时候，要不要列算式呢？怎么列算式？而参考书和课本上都没有，教师由于自身理解的不同，就出现了比较混乱的教学现象．

因此，估算教学的现状被教师们形象地描述为“三很”：教材很重视、教师很为难、学生很迷惑．

1.2 问题梳理

上述现象暴露出了当前估算教学中存在的一些问题，这些问题集中在对估算课程内容的理解和教学的认识及要求等方面．

1.2.1 内容理解

（1）本体性内容的逻辑关系认识不明确．

虽然估算的课程目标和内容标准在课标中已经比较明确，但是具体的知识层面内容则需要通过教材来呈现，由于教材版本较多，许多教材在编排上没有很好体现估算，导致估算的逻辑体系不太明确，教学素材有些混乱．从教学素材内容角度来讲，主要有3类估算：一是纯数学类估算，主要是直接给出数据来估算运算结果，要根据数据特点来估算，这在教材中主要安排在各种运算内容的学习中，表现为要求估算；二是应用类估算，常见形式是在应用题中，这种情况的最大特点是情境；三是计算时的估算，即检验结果是否正确，这种情况是应用估算监控笔算，此时估算通常表现为两种形式，先估算再笔算和先笔算再估算，这样就可通过估算来检验笔算，有助于学生养成检验习惯．其中，前两者是常见估算情境，这些情境本身可能就对估算提出了精确度要求；而计算时的估算目的是预估计算结果或者检验计算结果．这3类估算在教材中分散编排在各章节中，而且又需要根据不同具体情况灵活选择，从而导致师生对它们本身逻辑关系不明确．

（2）与其它内容之间的关系认识不清．

对于估算，有许多内容与其有密切关系，理清这些关系，能够反映数学学习和教学的整体联系思想，从而促进学生的数学理解．比如，估算与数感的培养以及实际生活的情境有密切关系，这是课标培训比较重视的方面．在国培课标培训中，有专家明确指出，估算是与具体情境联系在一起的，脱离具体情境不谈估算，估算是解决问题的一种策略．通过培训，教师们在这些方面是比较明确的．然而，对于估算和口算、精算、以及近似计算的区别和联系则比较困惑．在现实中的表现是，估算学习中发现许多学生在精算基础上再进行四舍五入得到估算结果，而评价中只关注结果却忽略了估算过程，从而导致学生的估算学习完全违背了课标要求的估算教学的要义．

（3）应用条件认识不足．

教学中经常见到的一种情况是：学生不知道在什么情况下选择用估算，而这时通过老师的教学传递给学生的信息是：一看见有“大约”“大概”等字样，就开始用估算来解决．例如这道题：

一个小型企业每月大约产生35千克垃圾，某村有3个小型企业，一年大约要产生多少垃圾？

对这个问题，许多学生是这样解答的：35×3=105，105 ×12=1 260，此解答显然是精算而不是估算，虽然本题中出现了“大约”字样．特别需要指出的是，“大约、够不够、能不能”这类表述的词语并不是要求估算的标志，不要一看到这些词就误认为是要求估算．其实，估算仅是解决问题的辅助策略之一，是为解决问题提供参考的．那么，这道题用估算来解答可不可以？单就数学题目的解决来讲，这是不合适的．但是作为解决这一问题的辅助手段是可以的：一个小型企业每月大约生产35千克垃圾，3个小型企业一个月大约100千克，这样的话一年就大约生产垃圾1 200千克，然后就可以对问题有一个初步结果，但这个结果是不能作为这一问题的答案的，这一问题的答案只能是精算的结果．虽然学生将35×3的结果自动地看作100是一种良好数感的体现，但这里的估算仅是一种解决问题的辅助手段而已．因此下面的认识是不妥的：认为这一问题有两种解决方法，一种是估算，一种是精算，只是精确度不同，由于估算的精确度低一些，所以两种方法相比较而言，精算比估算的方法要好．

（4）估算结果的科学评价标准不清楚．

由于估算结果的特点是不精确，因此会有多个结果，这些结果虽然没有对错之分，但是有精确度高低之分，所以这给估算的学习评价造成了困难．有相当一部分教师简单地用精算的评价标准去评价估算的结果，导致出现许多困惑．比如，若要求估算192+219的结果，有如下一些解答：

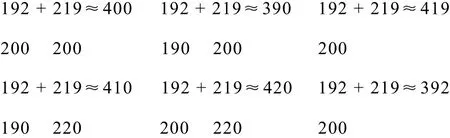
这些解答中，有的是估两个数，有的是估一个数，有的以百为单位，有的以十为单位．教师如何评价呢？首先必须肯定，这6种估算方法都是对的．其次，本题目涉及到量级的选择问题．课标中第一学段要求是“能结合具体情境，选择适当的单位进行简单的估算”，怎么理解适当的单位？对单位来讲，主要有两方面：一是计量单位，一是计数单位．这个题目涉及到计数单位的选择问题．这里的适当指的是要结合具体情境．对本题来讲，计数单位选择十或者百都是正确的，只不过精确度不同．因此，评价估算的好坏，虽然可以把精确程度作为标准之一，但不是唯一标准，有时问题情境发挥着重要作用，比如限制时间等．

1.2.2 教学认识和要求

（1）教和学的认识模糊．

什么是估算？它与精算（笔算）有何联系？为什么学估算？学估算有什么用处？在什么情况下用精算、什么情况下用估算？这些问题在学生和教师中比较常见，反映了很多一线教师和学生对估算的认识比较模糊，加之估算方法多样，估算学习评价标准不明确，而其它内容的评价标准不能简单地移植适用，这导致学生认为估算“只在课堂上有用”，而何时估算取却决于教师让估就估，缺乏对估算需要情境的认识．其实，估算的主要目的是做出一种判断或决定；就估算与精算的关系而言，估算是高于精确计算的一种综合能力，它与口算和数感具有密切的关系，估算课程内容主要涉及估算策略和估算方法．

（2）教学的阶段要求不明确．

估算的课程内容是有难度的，主要由3个因素决定：一是数字的特点，比如整十和整百要容易一些；二是所用的运算种类决定的，比如，一般来讲，乘法要比加法难一些，除法比乘法难一些；三是要求的精确度决定的，要求的精确度越高，越需要进行多次调整，这样就增加了难度．从难度上可以看到对于估算教学的阶段性要求，调查中发现，许多老师对估算的阶段教学要求不明确．如以下问题（人教版小学数学三年级上册第70页的估算教学）就是教学的一个难点：

每张门票8元，29个同学参观，带250元够吗？

教材中呈现的解法是：“因为29接近30，30×8=240．所以29×8≈240（元）”．教材设计这个题目的目的是让学生结合具体情境进行估算并解释估算过程，使学生体会到估算的必要性，进而找出可以把这个数看成最接近的整十、整百的数来估算的方法．即把29×8估算成30×8，刚好可以解决问题．这样，题目出得好，数字选得也好，让学生体验到了估算的价值，也就达到了教学的目的．因此，估算教学中，设计好的题目，斟酌好的数据，提出好的问题，对于在解决问题过程中培养学生的估算意识很重要．

但是，在教学中，许多老师则又把数据29改成32，这时仍用刚才的方法估算，取估算值240进行判断，就会造成估算结果与实际相矛盾的情况，这表明估算在这里暂时失效，但这是正常的．然而，对问题解决来讲还没有最终完成，还需要进一步思考：32比30多还是少？多多少或者少多少？仍然可以做出判断：在多2的情况下，会比估计值多2 ×8=16元，再考虑到240元，带250元显然是不够了．这里其实涉及到估算的二次调整问题，对三年级的学生来讲，难度就增加了，因此把这样需要二次调整能够有效解决的问题应放在更高的年级（对原题来讲，由于是把29×8估算成30×8，因此没必要考虑二次调整的问题），而对三年级学生就没必要，这里重要的是三年级学生估算意识的培养问题．本来题目是好题目，数据是好数据，一个题目解决一个问题，对三年级学生来讲，这样的问题就可以不讲，但是对个别学生的疑问应该耐心地给他们解答，如果听不懂的话，就告知题目的结果，要他们在课下或者查找相关材料进行学习，切不可非要一股脑把所有问题都集中到一起，这样由于集中了难点给学生的估算学习带来了更大的困难，因此估算的教学有个阶段性和发展性，不能一蹴而就．

2 解决策略

仔细研究问题出现的原因将有利于问题的解决，下面将在分析原因的基础上寻求解决问题的策略．

2.1 原因分析

虽然估算内容占数与代数领域的比重很小，但是却为什么会出现这么多的问题？其原因是多方面的，这里把主要原因归结如下：

（1）课程标准中对估算的课程内容界定不明确，系统性不强．

尽管2011版的义务数学课程标准对估算内容和要求做了进一步的修订、明确和深化，但是对于估算来讲，这些内容还是显得比较单薄．如，2011版的数学课程标准在学段课程目标和学段课程内容中分别对估算提出的要求是：

学段课程目标：第一学段：（知识技能·1）在具体情境中，能选择适当的单位进行简单的估算；（数学思考·1）在运用数及适当的度量单位描述现实生活中的简单现象，以及对运算结果进行估计的过程中，发展数感[3]．第二学段：（知识技能·1）理解估算的意义[3]．

学段课程内容：第一学段：（数与代数·数的运算·6）能结合具体情境，选择适当的单位进行简单估算，体会估算在生活中的作用（参见例6）[1]．第二学段：（数与代数·数的运算·9）在解决问题的过程中，能选择合适的方法进行估算（参见例26、例27）[3]．

由以上可以看出，尽管课标中对估算课程内容和要求有些界定，但是对教师来讲仍显得不明确，系统性不强．比如，在加、减、乘、除等各种计算中如何利用估算预估或者检验结果正确性等内容则在课标中的相关部分中都没有涉及．

（2）教师对估算课程内容理解不深且缺乏相应教学经验借鉴．

“教师对估算内容不熟悉、教学经验积累单薄以及过分追求估算解决问题的结果”也导致以上问题的出现．由于估算内容是在新一轮（第八次）基础教育课程改革中新添加的必学内容，所以教师在这方面缺乏成功的教学经验借鉴，而且易把以往一些关于精算的教学经验不适当地迁移到估算教学内容中．比如，许多老师认为估算的结果有唯一答案，当面对学生的许多答案时不知如何评判；当估算对解决问题无效时不知如何评判甚至对估算结果感到无法接受，等等．

（3）缺乏关于估算教学的专题性系统参考材料和针对性系统性的指导．

关于估算教学虽然已有许多研究，如有一些集中在估算能力、估算策略和估算意识方面[4～6]．从中国基础教育期刊全文数据库（1994—2012）中精确搜关键词“估算”共有5 616条记录，精确搜关键词“估算教学”共有349条记录；精确搜篇名“估算”共有1 540条记录，精确搜篇名“估算教学”共有222条记录．但是对于估算及其教学的专题性系统性研究和对估算及其教学的针对性系统性指导的研究明显不足，尚需作进一步研究和探讨．

（4）以往精算教学的思想根深蒂固地影响了估算的学习和教学．

在教学中经常见到，很多学生在做估算的题目时，会先把准确值算出来，再利用准确值来估算．究其原因，一是有些学生对估算的意义不理解，以为用正确值来估计是一个高明的办法，实际上是不明白为什么要估算；二是有些题目用笔算也很简单，学生觉得不需要估算就直接可以得出正确值，没必要用估算；三是教学时一般先学计算准确值，这样就使得学生有了先入为主的印象，影响了估算的学习．这样的估算教学，显然是与课标的要求是背道而驰的．事实上，课标中的估算是指在一定的范围内对计算结果的大致估计，它是在不要求准确值或者难以求出准确值的情况下，在允许范围内迅速找出的计算结果，目的是及时做出决策．因此，估算要比一般的计算要求更高，它更加挑战思维，要求学生要有良好的数感和灵活综合运用所学知识的能力．

2.2 策略建议

针对当前估算教学中的问题，结合原因分析，提出如下策略建议：

2.2.1 解决策略

（1）把握估算教学价值，确保育人价值实现．

估算的重要性日益突出，“随着社会的发展，人们越来越注意到估算的重要性．在很多情况下，估算结果与精算结果是同样适用的，甚至比精算结果更可取”[7]．估算课程内容在实验版和修订版课标中的确定和保持，标志着对估算教育价值的认可：应用估算不仅可以支持探索笔算方法，而且可以预测、解释计算结果、监控笔算的得数，表现为先估算再笔算和笔算后再估算等；同时，估算又是应用解决实际问题较广的一种有效方法．在数学课程中强调估算的主要原因，“一是与数学应用有关，毕竟日常生活中经常遇到的是估算而不是精确的计算，估算可以使数字与真实生活情境联结起来，不至于使数字失去意义，并能判断数字在情境中需要的精确程度；二是源自对数意识（数感）的重视．事实上，估算涉及理解数字大小、小数与分数系统、修正调整数字的能力．而这些能力均包含在数意识的几项特征中，因此，估算与数意识密切相关．若能拥有良好的估算能力，则对促进数意识亦有帮助”[8]．另外，估算作为检验精算是否正确的一种方法也是一个不可忽视的原因．

（2）正确定位估算与估算教学．

关于估算教学中出现的问题，要注意区分两个方面的问题：一是关于估算内容本身的问题；二是估算教学中的问题，前者反映的是学术数学层面，而后者反映的是课程数学层面．在教学中需要正确定位估算与估算教学．

学术数学定位．从数学的角度来看，估算是在算的基础上进行数量化的判断，它是一种从模糊到逐渐清晰的数量化过程，是一种在算基础上的合理假设和猜测．估算课程内容的学术数学定位有利于保证其正确性和合理性．这一定位主要是为估算的教学寻找科学的根据，尽管估算的课程内容与实际生活有密切的联系，但是作为课程的估算应该是有它的科学性的，离开的科学性是不能作为课程内容的，其科学性就来源于学术的数学，学术的数学保证估算课程内容的科学性．

课程数学定位．课程数学的估算定位，强调培养学生的估算意识、估算技能、估算能力和估算习惯（自动化）．在教学中，要注意根据估算目的尽可能追求估算结果的精确性、追求估算过程的合理性、追求估算评价的导向性．这一定位主要是从教育的视角来考虑的，即要从学生认知的视角来看待估算的课程内容，要结合学生的认知水平对估算的课程内容做出取舍，要进行教学法加工．

（3）坚持估算的特殊教学原则．

目前情况下，面对估算部分课程内容的教学，应该坚持哪些原则呢？

一是小学生认知水平性原则．估算的一些内容是受到学生已有的知识经验制约的[9]，要根据学生已有的知识经验来确定估算教学内容与方式，要注意多进行学情调研，切实把握学生的认知特点，有针对性地进行估算教学．

二是生活实际性原则．估算与生活具有密切的关系，自觉地运用估算有利于解决生活中的问题．教学中可以充分利用这一特点，贴近学生的现实，进行贴近学生生活的针对性地估算教学．“创设更多的机会接触现实生活和生产实践中的数学问题，使学生意识到在他们周围的某些事物中存在着数学问题，体会到估算的必要性和优越性．”[4]

三是估算意识渗透性原则．估算作为一种解决问题的策略，重要的是具有应用估算的意识，因此在估算教学中要特别注意渗透估算意识，帮助学生逐步养成自觉运用估算辅助解决问题或者正确及时做出决策的习惯．

四是直观性原则．数学的学科特点是具有抽象性，抽象性的数学课程内容非常需要直观性的解读，估算教学也不例外，特别是对低年级的估算教学，要善于借助合适的情境和呈现方式，在估算的过程中要注意运用以上提出的表征方式，这样的直观性教学有利于学生估算的学习．

（4）把握估算课程内容特征，采取针对性的教学策略．

一般来讲，估算内容具有4个基本特征：综合运算、方法多样、估算结果多种、应用广泛（主要为决策服务）．综合运算突出了估算在综合性的同时具有运算的特点；方法多样是指可以根据问题不同特点采用不同方法进行估算；估算结果多种是指估算结果不唯一，只有好坏之分而无对错之分，而区分结果好坏的一般标准是能否解决问题或者精确程度；应用广泛（主要为决策服务）是指一般强调直观整体上快速把握事情的全局，以利于做出决策及时处理面临的问题．针对这些特征，在估算教学中要注意选择针对性的教学策略．

一是要注意选择好的情境和问题．估算离不开情境，只有适合的情境才是估算教学所需要的，否则，估算教学就失去了应有之义，更达不到课标对估算教学的要求．同时要注意选择好的估算题目，要注意仔细斟酌题目中的数据，想清楚通过这些数据解决什么问题，这样才能确保真正的估算教学．

二是要注意估算教学的阶段性．估算教学内容中是有难度之分的，影响这种难度的主要因素有问题本身的难度、所用运算的难度和调整改进的难度．要注意按照课标的要求和学生的认知水平，恰当定位估算教学内容的难易程度，确保对估算意识和估算能力的培养要做到心中有数，循序渐进．

三是要对估算学习进行合理的评价．估算学习的评价之所以引起关注，主要是因为估算策略的多样化和结果的不唯一．对估算的评价，要注意引导学生对估算的策略进行优化，对估算的结果进行调整．估算学习的评价不是简单地对估算结果进行对错判断，而是要全面、科学和及时地对学生估算学习进程中的策略和结果做出评价，在评价时要注意评判估算结果好坏的标准：一是与估算的过程与方法有关系，对于一个估算问题，可以用多种方法进行估算，这些方法具有好坏之分而没有对错之分，好坏的标准是能否解决问题和精确程度；二是估算过程中要注意根据即时获得的信息进行及时的调整，确保估算能为正确决策提供帮助；三是估算的学习评价最好要求学生参与进来，让他们表达自己的看法，最后形成共识，这样有利于学生对估算内容的学习．“加强对估算的教学评价，虽然估算不同于精确计算，没有固定的答案，考查具有一定的难度，但评价的形式是多样的，因此可以采取不同的评价方式，在教学过程中评价，并把这些评价结果作为期末评价学生数学成绩的一个方面．”[4]

2.2.2 做法建议

（1）深入研读课标及其解读，切实把握教学的基本要求．

通过课标修订版的完善和课标解读，估算内容进一步得到了明确和深化，比如第一、二学段的课程内容标准分别是：能结合具体情境，选择适当的单位进行简单估算，体会估算在生活中的作用；在解决问题的过程中，能选择合适的方法进行估算．关于两个学段对于估算的要求，在课标解读中特别指出两者侧重点不同：

“第一学段的估算强调在具体的情境中选择合适的单位，例6中是选择了1 000人作单位．一般来说，估计教室的长度时，通常以‘米’为单位；估计书本的长度时，通常以‘厘米’为单位．也可以用身边熟悉的物体的长度为单位，如步长、臂长等，进而体会估算在生活中的作用．第二学段强调学生在解决问题的过程中，选择合适的方法进行估算．这个问题可以是实际问题，也可以是数学本身的问题．课标中的两个例子，一个是现实问题，一个是纯数学问题．例27就是一个数学问题．也可以鼓励学生用自己的方法进行估算．”[10]

又如，对于估算和精算的关系问题，在2011年版课标解读中做了解释：

估算在解决实际问题中经常用到，估算与精算相互补充，在实际运用中有不同的功能．对于一些问题可能只需要估算，没有必要一定要精算．如购物时，选择一些物品后，先估计一下大约需要多少钱，自己带的钱是否足够（课标例6）[10]．有时在精算的过程中也用到估算．如乘法运算时先估计结果是几位数，可以简单判断结果是否正确[10]．

以上这些解读或者解释，有利于教师明确和深入理解课标对培养学生的估算意识、估算技能、估算能力以及灵活选择合理的算法来解决问题的基本要求．

（2）整体梳理估算课程内容，逐步有序实现达标．

估算的课程内容在教材中比较分散，往往安排在相应的精确运算内容中，而在教学时则需要整体梳理估算各部分内容，以利于有序逐步实现课标中的要求．梳理方式方法有多种，比如可以大致归纳为如下几个方面：

一是估算概念、过程和策略问题．关于估算概念，有两种描述：一是侧重于发生过程，认为估算是通过心算而得到问题合理的近似答案的过程，具有“以快速的心算为主要计算方式，以合理的猜测代替精确的计算结果，心算、数概念及各种计算技巧的综合运用”的特点；二是侧重于本质层面，认为估算是指无法或没必要进行精确的数字处理或数字运算，只对其中的一种数量关系进行合理推断的一种能力，估算有时也是为了检验精算是否正确的一种方法；针对估算过程的调查研究认为，“在7年级学生直至成人中，好的估算者使用3种估算过程：一是精简，改变数据资料，即通过对数字的四舍五入、截断取值和兼容等相关的技能把数字重新改变成在心理上更友善的形式．如，用6+8+4来估算632+879+453，或用7 200÷60来估算7 431÷58；二是转化，改变问题的结构，即把数学结构改变为一个更容易的形式，如使用4×80来估算78+82+77+79的和，或者在估算百分数时转换为小数或分数；三是补偿，反映数学的变化，也即在心算之前或之后对结果进行补偿调整，使估算结果更接近精确值”[6]；针对估算策略研究显示，“一个好的估算者至少拥有3种策略（Sowder，1992）：一是重组，改变数字数据以改变心算；二是转换，把原来结构转成更易处理的形式；三是调整，计算中及计算后，可调整估计值至较接近的近似值．”[8]“研究表明，估算策略技能的短期指导、干预对四～五年级（10岁左右）儿童的估算策略选择有更大的影响”[6]．以上这些研究，有助于教师深刻理解估算的教学内容，从而提高对估算教学的认识．

二是估算的表征问题．估算中，有一个非常值得研究的问题就是表征问题，因为表征涉及到的是估算思维过程的呈现，因此对于估算学习、教学和研究具有重要意义．所谓估算表征，就是在进行估算时怎样即时记录估算的思考过程．在教学中怎样表征估算比较好呢？下面的做法值得

参考：

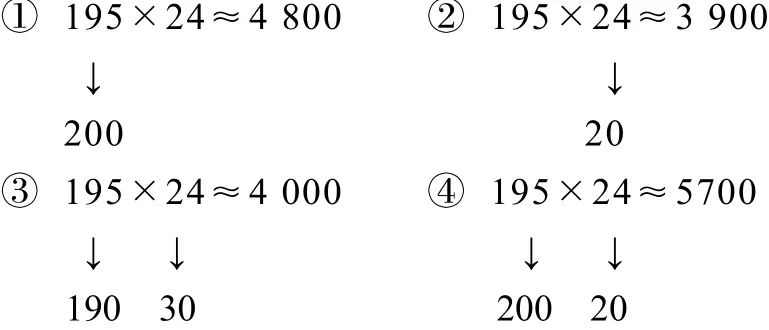
以上表征中，用“↓”表示把某数估为某值，没有估的数值就不用标出；用“≈”表示估算的结果．如①中表示把195估为200．初步的教学实践表明，这样的表征能够很好地暴露和展示估算的思考过程，有利于学生和教师对估算的学习和教学，同时有利于研究估算及其教学．

三是估算与其它知识之间的联系问题．若把估算当作孤立的点知识进行教学，肯定达不到课标要求的效果，这就需要建立估算与相关知识的联系．目前在估算的教材编写和教学中这一问题尤其突出．事实上，估算与其它知识具有密切的关系：估算是与精确计算（笔算、口算）相伴随的数的运算；估算是一种粗略的近似计算；估算可以渗透到测、计和算的各种情境中；从应用的视角来讲，不必要运用精算的时候大多可用估算来解决实际问题，可能也正是因为估算有情境要求才显出其不同于精算的教学价值．

四是估算的应用情境和估算意识的培养问题．估算的教学离不开估算的情境，何时用估算往往由问题的情境来决定．要注意根据情境来决定是否选择估算来思考和解决问题，“由于估算一般都与实际问题有关，因此，估算技能的训练应注意设置有意义的背景．研究表明，背景的使用在两个方面提高了学生的能力：首先，估算背景可以帮助学生克服将在该背景中所需的运算概念化的困难（如某数乘以比1小的数得到“更小的”数）；其次，估算背景还可以帮助学生回避运算规则的回答（如在使用小数时，能够在小数点后截去基本上没有意义的数位）（Morgan, 1988）．”[8]同时，要注意根据估算的情境灵活选择对已有数值的处理方法：大估、小估与大小估，必要时根据问题具体情况进行调整．估算的应用与估算意识具有密切的关系，一般来讲，估算意识越强，越有利于选择估算策略迅速做出决策或者解决问题，因此培养学生的估算意识有利于学生养成运用估算解决问题的习惯，同时也可以培养学生的数感．

五是关于估算结果与评价的问题．与精算最大的不同是估算的结果不唯一，其结果是一种模糊粗略直观的近似值，而且大多不准确，有时准确程度未必明确．估算结果与精确值的关系可以用精确度来衡量，一般来讲，越好的估算，精确度越高，但也有例外，比如估算结果还与目的、情境有关系．估算结果的评价是一个现实问题，估算虽然没有正误之分，但有好坏之别．那么，怎样的估算是好的或者好的估算的标准是什么？一般来讲，好的估算应该具备：估算的根据合理、策略方法科学（合自身的逻辑）和有利于达到解决问题的目的．估算的根据合理是指进行估算时要有根据，而且这一根据是有一定道理的；估算的策略方法科学是指估算合自身的逻辑，能够有助于正确地解决问题；估算有利于达到解决问题的目的是指估算的结果要尽可能地精确，能够有效地解决问题．

六是关于估算技能和能力的问题．估算技能是一种用估算来解决问题的本领，而多种估算技能的联合用来解决问题的本领则是估算能力．有研究者指出，“在学生估算之前，教师应首先让学生对数量做敏锐的判断．例如，对中年级学生而言，应该多让学生在解题前自己判断3 169+5 312与8 000哪个较大，而不只是机械地求出精确总和．事实上，估算是一种相当复杂的技能，若学生在发展上尚未达到估算能力，教师应避免估算技能的直接教学，否则将沦为没有理解的背诵．此外，估算的重点不在求出估计值，而是学习判断需要有多接近精确值（Sowder，1989）．因此，估算是决定答案是否合理的一种能力，这也是数感的特征之一．”[8]所以，估算能力是一种高于精确计算的综合能力，有些问题运用估算未必简单，特别是涉及二次甚至是多次调整的问题．例如，

一座桥限重3吨．一辆货车装了6箱货物，每箱285千克，车重986千克．这辆车可以安全过桥吗？

在本题中，若把285估成300，用“大估”法，得到的结果应比实际大，结合本题（桥限重）来讲是能够得到正确结论，即能安全过桥．而如果把285改为310千克，用“小估”法，得到的结论是能过；如果改为340千克，用“小估”法，得到的结论是不能过．事实上，要解决这些问题就需要估算的二次调整：若把310千克估成300千克，300×6=1 800千克，10千克×6=60千克，合起来也不超过2 000千克，再与986千克（不足1吨）合起来，不超过3吨，得到的结论是能过；而把340千克估成300千克，300×6=1 800千克，40千克×6=240千克，合起来超过2 000千克，还多40千克，再与986千克（比1吨少14千克）合起来整体估计，超过3吨，得到的结论是不能过．这种情况下问题虽然解决了，但太麻烦，甚至可能还不如用精算快，这样就不能体现出用估算解决问题的好处．在教学中若遇到这种情况，就需要根据实际情况灵活处理，而不一定必须要求用估算来解决这一问题了．［参 考 文 献］

[1] 马立平．美国小学数学内容结构之批评[J]．数学教育学报，2012，21（4）：1-4．

[2] 徐群飞．中美学生估算能力研究[J]．数学教育学报，2012，21（1）：73-75．

[3] 中华人民共和国教育部．义务教育数学课程标准（2011年版）[M]．北京：北京师范大学出版社，2012．

[4] 徐群飞，李俊．中小学生估算意识及策略的调查研究[J]．数学教育学报，2006，15（3）：64-67．

[5] 张云仙．学业不良生与学优生估算能力对比研究[J]．数学教育学报，2008，17（4）：49-52．

[6] 陈丽兰．小学四～六年级儿童估算策略选择的干预研究[J]．数学教育学报，2011，20（3）：63-66．

[7] 陈丽兰，刘鸣，曹景明．儿童估算策略选择研究述评及展望[J]．数学教育学报，2009，18（3）：83-86．

[8] 鲍建生，周超．数学学习的心理基础与过程[M]．上海：上海教育出版社，2009．

[9] 陈丽兰．9～12岁儿童估算策略选择的发展特点[J]．数学教育学报，2012，21（1）：48-51．

[10] 教育部基础教育课程教材专家工作委员会．义务教育数学课程标准解读：2011年版[M]．北京：北京师范大学出版社，2012．

Teaching on Estimation: Problems and Strategies

ZHENG Qing-quan
(1. Qilu Normal University, Shandong Jinan 250013, China; 2. Basic Education Curriculum Rensearch Centre of Shandong Province, Shandong Jinan 250013, China)

Teaching on estimation has attracted attention widely, there is a lot of confusion in the current teaching practice. Through the investigation some problems are found in content understanding the teaching cognition: logic of the content itself is not definite, understanding of the relationship between other knowledge is not clear, the application conditions of knowledge are lack, evaluation criteria to the results of estimation is not clear, understanding on teaching and learning is fuzzyand stage requirements on teaching are not clear. Some resolution strategies proposed to some problems above are: grasping estimation instructional value to ensure the realization of the value on educating people; correcting the positioning of the estimation and estimation on teaching; adhering to the special principles about estimation on teaching; grasping estimation courses content features, targeting strategies on teaching. Some suggestion is: studying deeply curriculum standards and their interpretation, grasping the basic requirements of teaching; arranging estimates course content overall, realizating the standards orderly and progressively.

teaching on estimation; problems; strategies

G420

：A

：1004-9894（2015）03-0096-06

[责任编校：周学智]

2014-12-26

山东省教育科学“十一五”规划2010年度课题——数学创新性教学的理论与实践研究（2010GG 224）

郑庆全（1972—），男，山东蒙阴人，博士，副教授，曲阜师范大学兼职硕士生导师，主要从事数学课程与教学论和教师教育研究．