“3+4”试点班中职生数学焦虑状况的调查研究

施 俊，陈建东，袁德正，丁先文

（江苏理工学院 数理学院，江苏 常州 213001）

“3+4”试点班中职生数学焦虑状况的调查研究

施 俊，陈建东，袁德正，丁先文

（江苏理工学院 数理学院，江苏 常州 213001）

数学焦虑是影响学生数学学习的重要非智力因素，基于中职与本科“3+4”分段培养模式的试点班中职生数学基础薄弱，对他们的数学焦虑的调查研究意义更加重大．通过调查发现，应试焦虑、解题焦虑、学习焦虑和应用焦虑是试点班学生数学焦虑的主要来源；数学学科认识、数学自我效能感、数学学习归因方式和数学学习兴趣是试点班学生数学焦虑的主要成因．

试点班；中职生；数学焦虑；因子分析法

1 研究背景

为了满足社会经济发展和产业转型升级对高端技能型人才的亟需，全国加快了推进现代职业教育体系建设的步伐，各地先后启动了现代职业教育体系建设试点项目．如2012年江苏省立足于探索中等职业教育与高等职业教育、中等职业教育与应用型本科教育、五年制（或三年制）高等职业教育与应用型本科教育分段培养的人才培养模式，按照“专业对接、课程体系衔接、实践导向、中高职与本科一体”的建设思路，在苏州、无锡、常州、南京和南通5个实验区的一些中高职校和本科院校设立了试点班，具体探索中高职与本科分段培养机制．中职与本科“3+4”分段培养就是其中的一种试点培养模式．

中职与本科“3+4”分段培养，即学生在中职校进行3年中等职业教育，再到应用型本科院校完成4年本科教育．它将取消中等职业学校毕业生升入应用型本科的统一考试，改由对接本科将教学要求渗透到中职校，学生只需通过重要基础课程（语、数、外）、专业核心课程和技能水平等的转段审核，即可升学进入本科院校接受本科教育，是一种培养高端技能型人才的人才培养模式．

中职与本科“3+4”分段培养模式的实施，关键是课程体系的科学合理的衔接，数学作为一门重要基础课程，对于试点班的中职生是至关重要的，学习好坏直接影响本科阶段的进一步学习、后续专业课程的学习和思维能力的培养．在没有升学外部压力情况下，鉴于数学内容的高度抽象性、应用的广泛性等特点，容易使许多数学基础本来就不怎么好的试点班中职学生对数学的学习望而生畏，缺乏应有的兴趣和信心，甚至可能产生不当的焦虑情绪（即数学焦虑）．数学焦虑是由数学问题和情境而引起的病态恐惧症，是在学习数学的过程中产生的恐惧感、急躁感等不良的情绪反应[1]．它是影响数学学习的重要的非智力因素，是一种负性情绪，是由数学而产生的认知性恐惧情绪，会导致学生逃避数学，造成学生数学学业成绩的低落[2]．它能影响学生对自己能力的判断，使自己的数学学习效能感降低，学习自信心降低，不同的数学焦虑水平其数学成绩有显著的差异[3]．过高或过低的数学焦虑都影响数学活动的进行，不利于数学学习，并且长期的数学焦虑会使学生形成消极的数学态度，而消极的数学态度又会导致错误数学观的形成．适度的焦虑是一种正常的心理状态，它可以推动人积极向上，应付即将发生的危机，是个体不断进取的内在动力，适度的焦虑可取得最佳的学习效率[4]．所以，研究试点班学生数学焦虑状况，客观地认识学生数学焦虑程度、分析数学焦虑成因，以帮助调节和指导学生不适当的数学焦虑，进行有效的数学学习，提高数学成绩，培养必要的数学思维能力，是此研究的目的．

2 研究方法

2.1 研究目的

试图调查试点班学生的数学焦虑程度及来自于学生自身（数学学科认识、学习动机、数学自我效能感、数学学习归因方式、学习兴趣、学习习惯方法、学习态度等）和教师（教学方法和行为方式）的影响因素，对调查结果进行统计分析，探索有效的教学策略，促进试点班中职数学与大学数学教学的更好对接．

2.2 研究工具

调查要构建两个量表：数学焦虑量表和数学焦虑成因量表．数学焦虑量表是研究学生数学焦虑水平的工具，通过度量学生在各种具体数学情境（如上课、考试等）中表现出的数学焦虑程度，综合分析其数学焦虑水平．数学焦虑成因量表是考察影响数学焦虑水平的主要内源性和外源性因素，即学生自身的特征和教师行为，如数学学科认识、学习动机、数学自我效能感、数学学习归因方式、学习兴趣、学习习惯方法、学习态度、教师教学等．两者在构建方法上基本类似．2.2.1 数学焦虑量表的构建

根据有关文献[5～11]结合研究目的针对试点班中职生特点自编了数学焦虑问卷，为了初步考察自编问卷的结构和检验每一项目的质量，随机抽取了江苏省武进中等专业学校计算机网络技术专业、汽车运用与维修专业两个试点班90人进行了预试，用SPSS 21.0对预测数据进行了项目分析和初步的因子分析，删除了一些因子负荷较小的题目．另一方面，对因子负荷矩阵进行分析发现，一些项目在不同的因子上有相近的负荷，说明区分度不高，也予以删除．最后，形成了数学焦虑问卷，该问卷共分11个内涵无交叉重叠的维度：学科焦虑、课堂焦虑、应试焦虑、考试结果焦虑、解题焦虑、学习焦虑、应用焦虑、被观察焦虑、观察焦虑、教师焦虑和家长焦虑．学科焦虑，是指对数学学科的认识或感受而引起的畏惧心理，如“只要提到数学，我就感到头疼”；课堂焦虑是特指等待上数学课及在上数学课的过程中产生的焦虑情绪，如“上数学课时，总是怕听不懂”；应试焦虑是指在数学考试及其相关情境中的焦虑表现，如“在数学考试时我常因为过度紧张而把应该会的却忘记了或做错了”；考试结果焦虑，是指由别人对自己考试成绩不佳的态度所引起的焦虑情绪或者自己对考试结果的担忧，如“我担心老师公布数学成绩”；解题焦虑，指在已有数学知识技能的基础上解答数学问题的过程中产生的畏惧情绪，如“我害怕应用题，担心题目读不懂”；学习焦虑，特指学习新的内容的过程中产生的焦躁情绪，如“当我学习一个定理的证明或一个公式的推导时，我会焦虑”；应用焦虑，特指在专业课学习中用到数学知识时产生的焦虑，如“在数控机床加工的手工编程中，老师要求利用参数方程来准确描述零件轮廓的几何形状时，我很紧张”；被观察焦虑，指被别人注意到自己回答问题或解题时产生的焦虑情绪，如“当老师提问或上黑板板演，结果答不出来或答错了，我会很紧张”；观察焦虑，指看到或听到别人讨论数学问题时产生的焦虑情绪，如“听到同学们讨论数学题时，我会紧张”；教师焦虑，是指因教师对自己数学学习的要求、期望和态度所引起的焦虑心理，如“如果数学老师对我的期望高，我会觉得压力很大”；家长焦虑，是指因父母对自己的数学学习的要求、期望和态度所引起的焦虑心理，如“我担心父母对我的数学成绩感到失望”．采用内部一致性信度和分半信度对问卷进行信度检验，各维度筛选出一个与整个问卷的一致性系数最高的题目，形成了由11个问题构成的数学焦虑量表，各维度问题及总问卷的内部一致性系数分别为0.694 2、0.629 3、0.627 8、0.729 6、0.589 7、0.614 8、0.668 7、0.529 2、0.642 8、0.724 3、0.591 8、0.782 2，总调查问卷分半信度为0.752 7，有较好的结构效度．

数学焦虑问卷题目得分采用Likert 5级评分法．“完全符合”得5分，“基本符合”得4分，“无法确定”得3分，“基本不符合”得2分，“完全不符合”得1分．每题只有一个答案．

2.2.2 数学焦虑成因量表的构建

类似于数学焦虑量表，另构建了数学焦虑成因问卷，该问卷涉及因素：教师教学方法和行为方式、数学学科认识、学习动机、数学自我效能感、数学学习归因方式、学习兴趣、学习习惯方法和学习态度等，共35个题目，各因素内部一致性系数分别为0.556 8、0.682 9、0.729 8、0.623 8、0.612 5、0.738 2、0.581 4、0.692 7．

数学焦虑成因问卷题目得分也采用Likert 5级评分法．每题只有一个答案，要求学生选择最符合自己观点或情况的一项．得分选项同数学焦虑问卷．

2.3 研究对象的施测分析

目前，与江苏理工学院进行中职与本科“3+4”分段培养的中职校一共有6所，于2014年5月—2014年7月采用问卷调查法在江苏省无锡机电高等职业技术学校、江苏省无锡旅游商贸高等职业技术学校、江苏省宜兴中等专业学校和江苏省武进中等专业学校、江苏省镇江高等职业技术学校和江苏省扬州商务高等职业学校6所中职校的2013级数控技术、计算机网络技术、汽车运用与维修、电气自动化技术、工艺美术、国际贸易和旅游管理等专业的634名试点班学生进行了一次数学焦虑测评，共发放调查卷634份，收回618份，剔除作答不全和无效的16份，有效率95%．

全部数据统计分析由SPSS 21.0完成，运用因子分析法进行探索性分析．

针对数学焦虑量表中的调查数据，由于不存在度量单位，直接利用协方差矩阵进行因子分析，取特征值均大于1的公因子且累计方差贡献率大于80%的公因子，经过方差极大旋转，最终获得6个因子，计算结果如表1．

表1 公因子方差

表1是提取的6个公因子在11个焦虑维度上的方差贡献及其贡献率，表2是公因子的总方差贡献及其贡献率，表3是6个公因子和11个焦虑维度之间的数学关系．

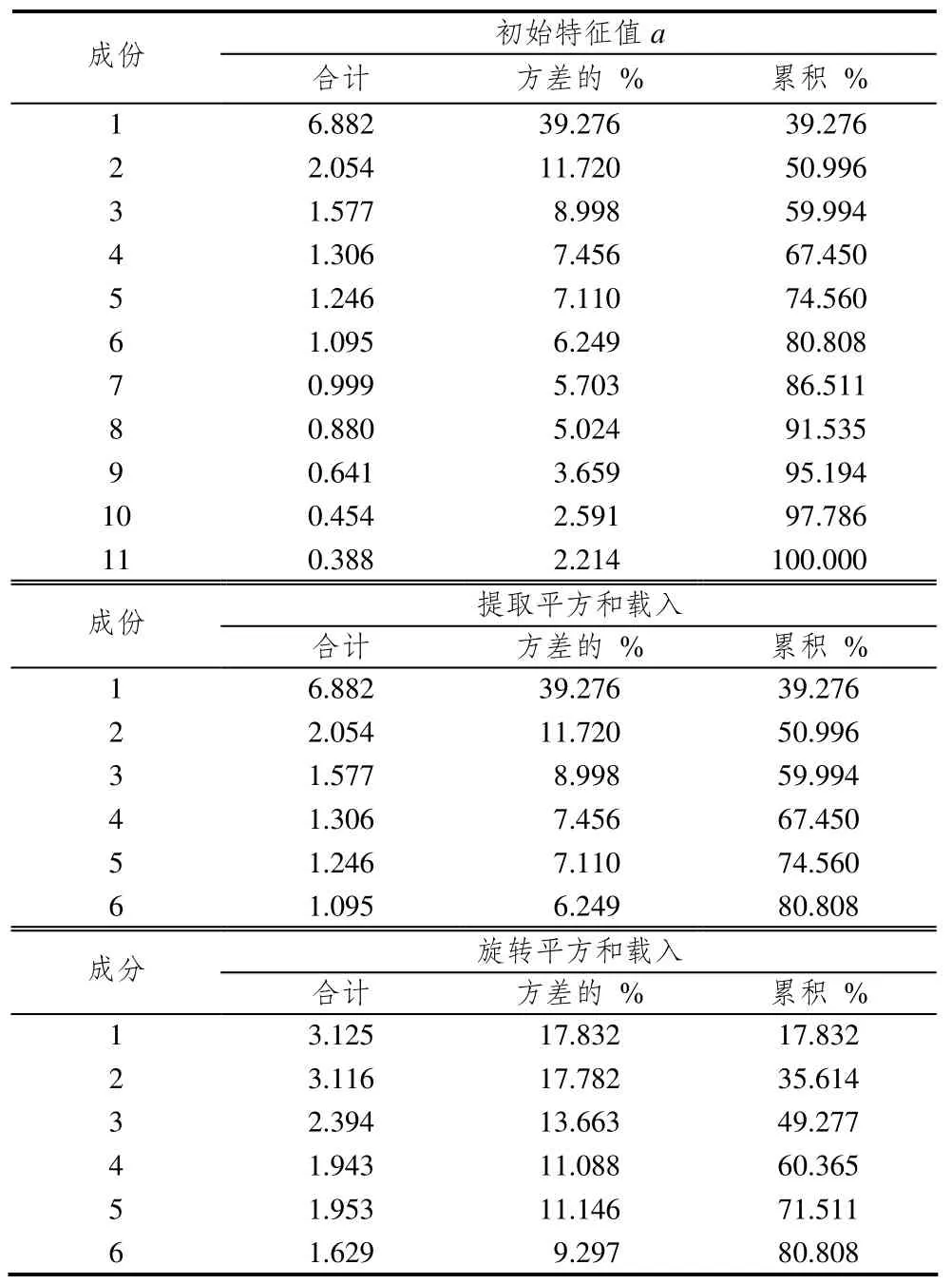
表2 总方差

3 研究结果

通过表1—表3中的因子特征值，旋转成份矩阵系数和得分公式[12～13]，合并计算得出下面的数学焦虑综合得分公式（非标准化）：

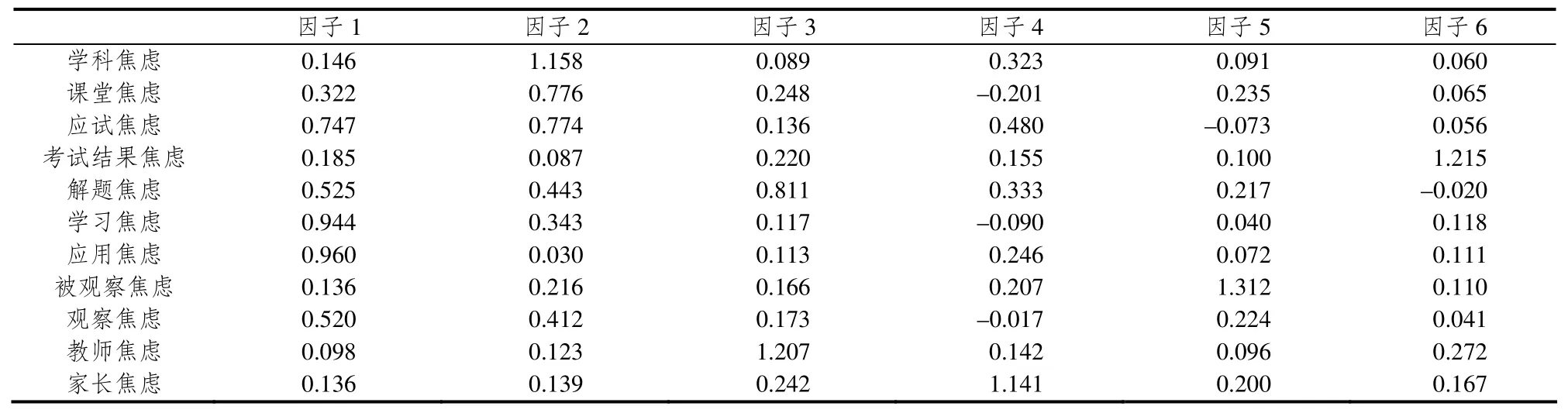
表3 旋转成份表

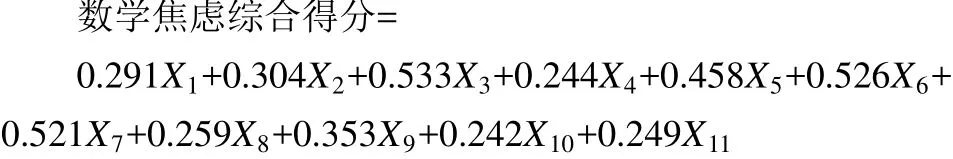
其中，X1–X11是指数学焦虑量表中的11个焦虑维度．

根据被测学生数学学习焦虑综合得分，对学生的数学焦虑进行划分，将焦虑得分在1—2分之间统称为低度数学焦虑，记为等级I；4分以上属于高度数学焦虑，记为等级Ⅲ；其余属于中度数学焦虑，记为等级Ⅱ．统计结果见表4．由表4可以看出：大多数学生的数学焦虑是适度的（II级焦虑为74%），对其数学学习是有益的．低度焦虑和高度焦虑之和达到了约26%．这部分学生不容忽视，后又由这些学生的数学任课教师对他们进行了深入访谈，了解到：高度数学焦虑者39人中，31人的数学成绩相对较差，在班级里处于中等偏下，只有8人数学成绩中等，他们中大多数数学学习目标明确，学习态度也较端正，但学不得法对数学不感兴趣；低度数学焦虑者116人中，61人的数学成绩较差，在班级里处于末等，对数学学习不感兴趣，对数学学习抱着无所谓的态度，有13人数学成绩中等，有42人数学成绩较优秀，他们数学学习目标明确，学习态度也较端正，具有良好的学习习惯和高效的学习方法，对数学有浓厚的兴趣．

表4 试点班数学焦虑统计

统计结果表明：试点班学生的总体数学焦虑处于中等偏下水平；各个焦虑维度都在专业方面没有显著性差异，男生和女生在数学焦虑方面不存在显著差异．从数学焦虑综合得分公式中可以看出，在11个维度中，应试焦虑、解题焦虑、学习焦虑和应用焦虑的系数较大，对评价学生数学焦虑水平的影响程度较大，考试结果焦虑、被观察焦虑、教师焦虑和家长焦虑的系数相对较小，对评价学生的焦虑水平影响较小．因此可见，应试焦虑、解题焦虑、学习焦虑和应用焦虑是影响试点班学生数学焦虑的重要来源．

4 相关分析

针对数学焦虑成因量表，先利用因子分析构建各个成因的综合得分，然后计算它们与数学焦虑的相关系数，为了减少评分取值的影响，采用Kendell相关系数[12～13]，结果见表5．

4.1 数学学科认识与数学焦虑

试点班学生的数学学科观念与数学焦虑呈负相关（相关系数为–0.357），且显著性水平小于0.01，这表明数学观的认识程度影响数学焦虑的水平．对数学学科的认识越清晰，越不容易进入高焦虑状态；对数学学科的认识越迷茫，越有可能进入高焦虑或低焦虑状态．因此，有必要提高学生对数学学科的认识．

4.2 数学自我效能感与数学焦虑

试点班的数学自我效能感与数学焦虑存在显著相关（相关系数为–0.312），且显著性水平小于0.01，这说明数学自我效能感越强，越容易达到适度的数学焦虑．因此，提高学生的数学学习成就感能有效平衡其数学焦虑．

4.3 数学学习归因方式与数学焦虑

试点班的数学学习归因方式与数学焦虑存在显著相关（相关系数为–0.285），且显著性水平小于0.01，这说明积极的归因方式，会影响数学焦虑水平．因此，教师应积极帮助学生改进其数学学习的归因方式．

4.4 数学学习兴趣与数学焦虑

试点班的数学学习兴趣与数学焦虑呈显著相关（相关系数为–0.158），且显著性水平小于0.05，这说明兴趣可以帮助学生数学焦虑水平达到适度．

4.5 数学学习动机与数学焦虑

试点班学生的数学学习动机与数学焦虑呈显著负相关（相关系数为–0.139），这说明数学学习动机对数学焦虑有一定的影响，在一定程度上学生若能积极主动进行数学学习，将会有助于其达到适当的焦虑水平．

4.6 数学学习习惯及方法与数学焦虑

试点班的数学学习习惯方法与数学焦虑显著相关（相关系数为–0.135），这在一定程度上说明好的数学学习习惯和方法对学生的数学学习是有帮助的．

4.7 数学学习态度与数学焦虑

试点班的数学学习态度与数学焦虑呈显著负相关（相关系数为–0.135），这一定程度上说明好的数学学习态度对学生的数学学习也是有帮助的．

4.8 教师教学行为与数学焦虑

教师的教学方法和行为方式是影响试点班学生数学焦虑的重要外源性因素．教师的教学方法和行为方式与数学焦虑呈显著负相关（相关系数为–0.122），数学教师幽默风趣、和蔼可亲的教学风格可以提高数学课堂效率，使教学内容易于接受，数学教师的表扬与鼓励可以激发学生对数学的兴趣和积极性，数学教师高明的教学水平可以确立学生正确的数学观以及学好数学的信心．

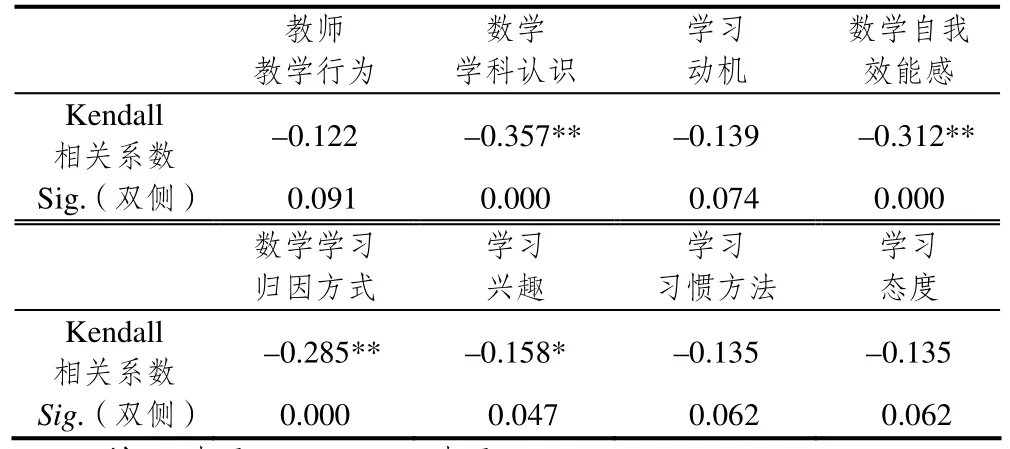
表5 数学焦虑相关因素分析

综上，教师教学行为、数学学科认识、学习动机、数学自我效能感、数学学习归因方式、学习兴趣、学习习惯方法、学习态度与试点班学生的数学焦虑均呈负相关，这些都是影响学生数学焦虑的重要成因．尤其是数学学科认识、数学自我效能感、数学学习归因方式的显著性水平小于0.01，学习兴趣相关性的显著性水平小于0.05，这4个因素是试点班学生数学焦虑的主要成因．

5 教学建议

文[14]分别从学生心理治疗的、数学学科特征（趣味性、应用性等）、教学语言和行为及学习方式等角度给出了预防和消除数学焦虑的策略：帮助学生分析焦虑的真正内容和根源；消除学生对数学的神秘感和恐惧感；使用暗示技术和鼓励合作学习．文[7]提出通过创设“趣、新、活”的课堂学习情境、营造轻松愉悦的学习氛围、在教学各环节实施分层次教学有效调整中职生不适度的数学焦虑．这些调节学生数学焦虑的方法具有普遍适用性，当然也适合“3+4”试点班学生．另外，针对研究结论进一步提出几点教学建议．

5.1 培养正确的数学观和积极的数学学习归因方式

研究中发现数学学习观、知识观与数学焦虑呈极为显著的负相关，因此，教师在数学课堂教学中应该潜移默化地培养学生树立正确的数学知识观和数学学习观．

积极的数学学习归因有利于增强学生学习的自信心、消除数学焦虑情绪，正确看待学习上的成败，客观分析学习成败的原因，积极寻求科学有效的学习方法和更加端正的学习态度．所以，数学教师在平时的教学和管理工作中要注意引导学生形成正确的数学学习归因观念．

5.2 增强学生数学自我效能感

试点班学生在初中时期多数数学成绩不够理想，大多数存在自卑心理，早已丧失了自信心，数学焦虑水平较高，而数学自我效能感与数学焦虑相关性相当明显，因此，必须增强学生数学自我效能感，树立学好数学的信心．一方面要善于运用鼓励教育，用平等的、亲切的语气、鼓励的语言与学生交流，用宽容的态度感染学生，教师应该清楚地告诉学生：在数学学习上人人都会犯错．学生出错时应耐心引导指正，使他们能够在教师的帮助下顺利掌握学习内容，从而在数学学习中体会到成就感，达到增强数学自我效能感的目的；另一方面要巧用赏识教育，赏识学生是维护学生尊严的体现．如在课堂上较容易的问题，鼓励基础较差的学生积极发言，让他们获得成功表现的机会，及时表扬，增强其自信心．

5.3 优化课堂教学方法和内容

数学是试点班的一门重要核心基础课，对学生升入本科进一步学习和专业课的学习都是至关重要．而这些学生数学基础普遍较普通高中生要差一些，对数学学习的兴趣自然就不高，越是对数学产生浓厚兴趣的学生越不易产生数学焦虑，越是对数学没有兴趣或兴趣极低的学生，越容易产生数学焦虑[15]．显然，让学生感受数学的实用性，了解数学的价值，体会数学的奥妙是提高学生数学学习兴趣的有效途径．因此，在教学中教师本着“数学课要满足专业核心课程的需要，为专业核心课程服务”的主导思想，本着“必需，够用”的原则，精心设计教学内容．数学教师在课堂教学过程中不要刻意追求学科体系的完整性，淡化纯形式化的理论推导与证明，注重基本概念的理解、基本数学方法的掌握与实际应用的介绍，尽量能将数学知识与专业背景、实际应用有机结合．比如，可以与专业课教师合作共同发掘一些运用数学知识解决的简单专业问题，融入到数学教学当中．另外，数学教师还要在教学方法的设计等方面多下功夫，一要注重知识产生背景的设计，注重概念形成过程的建构，比如可以充分利用现代教学手段创设教学情境，将抽象的深奥的数学知识具体化、直观化、动态化、趣味化，打破数学的神秘感，激发学生对数学学习的兴趣．二要根据学生的认知结构和规律，针对他们活泼、好奇、好胜等心理特征，充分引入竞争机制、善用鼓励，激发他们的数学学习积极性和兴趣．

5.4 严格过程性考核机制

对于试点班学生，由于学习环境宽松，多数自控能力较差、数学基础薄弱、数学学习兴趣不高，所以数学学习的内部动机整体不强．另外，由于不需要进行选拔性考试，没有升学压力，数学学习的外部动机也不高．这就导致很多同学数学焦虑水平很低，不利于数学学习，所以，必须严格过程性考核机制，将每学期期末成绩纳入转段考核中，适当增加点压力．

5.5 重视学习习惯和方法的培养

试点班学生中有许多学生解题缺乏周密思考，一般没有预习和复习的习惯，上课注意力集中时间较短，更没有做笔记、整理笔记和归纳总结的习惯，也缺乏有效的学习方法．因此，数学教师不仅要为学生明确学习目标，激发学生的学习兴趣，还要帮助学生养成良好的学习习惯，教给学生一些较有效的数学学习方法，使学生在获得必要的基础知识的同时，进一步掌握一些基本的数学思想和方法，发展抽象思维和逻辑推理能力，培养熟练的运算能力、综合运用知识分析问题和解决问题的能力．

5.6 帮助数学学差生拟定焦虑转化策略

调查反映，高度数学焦虑的学差生一般学习态度较好，但知识结构凌乱，也不完整，更没有好的学习习惯．低度数学焦虑的学差生有相当一部分处于“学习脱轨”和“恶性循环”状态，学习没有兴趣，对数学学习抱无所谓的态度．因此，要优化外部环境，激活外部机制，选点切入，多管齐下．数学教师应做好以下工作：

（1）重视数学学差生的焦虑状况，提高对转化数学学差生的认识，转化学差生是实施中职与本科“3+4”分段培养模式，培养高端技能型人才的需要；（2）关心同情学差生，善于激励后进生，树立转化的信心；（3）对学差生进行诊断，查找其原因，了解学差生的个性特征，明确学差生的类型，对症下药；（4）进行情感沟通，取得学差生的信任，和他们交朋友；（5）帮助学差生制定适合他们的学习目标，进行知识技能、思考方法、学习方法等全方位指导，由易到难，小步子、小转弯、小坡度；（6）发现学差生有进步，要及时表扬和鼓励；（7）培养学差生正确的数学学科观念、积极的数学学习归因和正确的自我效能感，关注他们的数学焦虑水平；（8）允许学差生有反复，要有耐心，必要时要发动其他学生、家长等帮助．

[1] 王凤葵，罗增儒．数学焦虑的研究概况[J]．数学教育学报，2002，11（1）：39–42．

[2] 胡传辉，肖慧．数学焦虑影响因素探析及教育启示[J]．教学与管理，2007，（6）：76–77．

[3] 熊建华．中学生数学焦虑及相关因素的调查研究[J]．数学教育学报，2008，17（3）：52–54．

[4] 李荣，吕传汉．“数学情境与提出问题”教学模式对缓解贵州初中生数学焦虑的探究[J]．数学教育学报，2004，13（4）：88–89．

[5] 肖慧．中学生数学焦虑及其内源性影响因素研究[D]．南京师范大学，2007．

[6] 熊建华．中学生数学焦虑及相关因素的调查研究[D]．南京师范大学，2005．

[7] 蔡国菁．中等职业学校学生数学焦虑的成因与对策[D]．山东师范大学，2009．

[8] 周洁．高职学生数学焦虑的现状与成因[D]．华东师范大学，2010．

[9] 刘人瑞．中职生数学学习的现状及教学策略研究[D]．东北师范大学，2012．

[10] 彭乃霞，廖爽，陈亚萍．非数学专业大学生数学焦虑成因分析及对策研究[J]．数学教育学报，2011，20（3）：47–50．

[11] 李顺雨，田澜，李宏翰．高中生数学学习适应性问卷的初步编制[J]．数学教育学报，2013，22（4）：62–65．

[12] 方开泰．实用多元统计分析[M]．上海：华东师范大学出版社，1989．

[13] 朱建平．应用多元统计分析（第二版）[M]．北京：科学出版社，2012．

[14] 谢明初．数学学习焦虑的预防与消除[J]．数学教育学报，2002，11（1）：43–45.

[15] 罗新兵，王凤葵，罗增儒．中学生数学焦虑的调查与分析[J]．数学教育学报，2008，17（5）：48–50．

Investigations on Mathematics Anxiety of Secondary Vocational School Students of the Pilot Classes Based on “3+4”

SHI Jun, CHEN Jian-dong, YUAN De-zheng, DING Xian-wen
(College of Mathematics and Physics, Jiangsu University of Technology, Jiangsu Changzhou 213001, China)

Mathematics anxiety is an important non-intelligence factors affecting student learning mathematics, the pilot class students base on "3+4" staged cultivation mode of secondary vocational and undergraduate education is weak in mathematics, it is more significant to research of their mathematics anxiety. Through investigations, it can be concluded that exam anxiety, problem solving anxiety, learning anxiety and application anxiety are the main source of the pilot class students mathematics anxiety; cognition of mathematics subject, mathematics self-efficacy, mathematics study attribution style and interest to mathematics study are the main causes of the pilot class students mathematics anxiety.

pilot class; secondary vocational school students; mathematics anxiety; factor analysis

G420

：A

：1004–9894（2015）03–0091–05

[责任编校：陈隽]

2015–01–04

2013年江苏理工学院教学改革与研究项目——职业高中数学与大学数学教学衔接研究（JG13021）

：施俊（1976—），男，山西朔州人，硕士，讲师，主要从事数学教学与课程论研究.