中美高中数学教材的习题比较及启示——以PEP教材与UCSMP教材中平面向量章节为例

林 丹，胡典顺

（华中师范大学 数学与统计学学院，湖北 武汉 430079）

中美高中数学教材的习题比较及启示
——以PEP教材与UCSMP教材中平面向量章节为例

林 丹，胡典顺

（华中师范大学 数学与统计学学院，湖北 武汉 430079）

教材建设是中国新一轮数学课程改革的重要标志，是改革理念和要求的具体体现．通过对人教版高中数学教材与美国UCSMP教材中向量章节习题的比较发现，UCSMP教材的习题呈现方式丰富，编排具有层次性，素材来源与实际生活更紧密，注重较高认知水平的培养，注重习题的探索性和开放性，难度较大；人教版教材习题类型丰富，较高认知水平习题较少，难度恰当，注重基础性，探索性、开放性问题较少．在教材编写中，人教版高中数学教材可以适当考虑丰富习题的呈现方式，提高较高认知水平习题比例，增加探索性和开放性习题，注重习题背景的多样化，紧密联系生活实际．

数学教材比较；平面向量；习题；启示

1 问题提出

教材建设是中国新一轮数学课程改革的重要标志，是改革理念和要求的具体体现[1～2]．习题是中学数学教材的重要组成部分，习题配置在一定程度上反映了数学教材编者的价值取向和编写风格，习题对学生数学概念的理解、数学技能的掌握和数学思想方法的掌握具有不可估量的作用，也对数学课堂教学产生不可忽视的影响．对中美两国高中数学教材中的习题进行比较，分析两国教材在习题配置方面不同的风格、倾向及特色，对中国的数学教学改革和高中数学教材习题的编写是很有必要的．

人民教育出版社出版的教材在中国得到广泛的使用．在美国，每年有几百万中小学生使用The University of Chicago School Mathematics Project教材（以下简称“UCSMP教材”），该系列教材是体现美国课程改革及发展方案的典型代表．UCSMP教材强调基本训练，重视能力培养，着眼于数学应用意识和问题解决[3]．向量是近代数学中重要和基本的数学概念之一，是沟通代数、几何与三角函数的桥梁．在新一轮数学课程改革的背景下，《普通高中数学课程标准（实验）》中平面向量知识的份量进一步增加．向量又具有数形结合的重要特征，既有几何特点又有代数意义，是数学教材中非常重要的数学知识．因此，选取人民教育出版社《普通高中数学课程标准实验教科书（A版）》（2007版）中必修4[4]（以下简称“PEP教材”）和UCSMP教材（2010版）第六册[5]中平面向量部分作为比较内容，研究中美两国这部分知识习题的配置情况，为教材平面向量部分的习题编写提供参考建议．

2 研究方法

PEP教材中平面向量的知识是安排在必修4第二章，UCSMP教材中平面向量的知识安排在第六册第十二章前4个小节（后面4个小节的内容是空间向量，由于这里主要是比较平面向量的知识，所以不考虑UCSMP教材中空间向量的知识）．采用文本质性分析与定量刻画相结合的研究方法，从习题的呈现方式、数量、类型、认知水平以及难易程度5个方面进行比较研究．

（1）习题的呈现方式：根据教材中的习题栏目设置进行详细分析．

（2）习题数量：UCSMP教材和PEP教材中的习题均有两种形式：含有一个小问题的习题和含有多个小问题的习题．例如UCSMP教材以阿拉伯数字1，2，3……标注习题题号，用小写字母a，b，c……表示下设的小问题题号；PEP教材也以阿拉伯数字1，2，3……标注习题题号，但是用（1），（2），（3）……表示下设的小问题题号．为统一标准，以阿拉伯数字1，2，3……出现的次数为准来统计习题数目，即以大题计，一题多问的按照一题计算，考虑到习题类型中的题型也需要统计题目，判断题和选择题以小题计算．

（3）习题类型：将习题分为：选择、填空、判断、解答、证明、作图等6种常见题型，并对它们分别进行统计．统计方法同习题数统计方法．

（4）习题的认知水平：布卢姆等的《教育目标分类学》在认知领域有6大类别：知识、领会、运用、分析、综合、评价．他的分类理论由于缺乏可靠的实证，其在连续性和层次性方面存在漏洞．鉴于此，顾泠沅等先后两次（1990，2007）进行大样本测试，从大量外显行为所表征的教学目标中析取内隐主要因素，由此确定目标框架的层次并研究分类的连续性[6]．最后经过改造，数学认知水平分析框架分为4层次架构：水平1：计算——操作性记忆水平；水平2：概念——概念性记忆水平；水平3：领会——说明性理解水平；水平4：分析——探究性理解水平．其中，水平1、2为记忆水平，为较低认知水平．水平3、4为理解水平，属于较高认知水平，第4水平通常称作高认知水平．水平1层次的习题只需要学生按照教材所明确要求的程序或方法进行基本的运算；水平2层次的习题是考察学生对课本概念、规则、表达形式记忆的题目；水平3层次的习题需要学生理解概念、定理、法则等的内涵和外延，从而能够根据课本例题，选择合适的数学方法，灵活运用所学知识解决一些常规问题；水平4层次的习题需要学生对之前没有接触过或没有现成解决方案的非常规问题（开放题、探究题）进行分析，创造性地解决问题[7]．

（5）习题难度：根据相关学者建立的综合难度模型[8]，对两版教材平面向量章节中的习题进行统计分析，其中包含了5个难度因素：探究、背景、运算、推理、知识含量，具体如下表1所示：

表1 综合难度因素表

计算习题综合难度时采用如下计算公式：

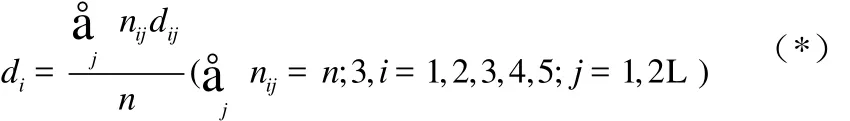
3 研究结果与分析

3.1 习题呈现方式

习题的呈现方式在一定程度上体现了教材编写的特色，两版教材的主要习题呈现方式如表2所示．

表2 两版教材习题呈现方式的比较

分析表2可知，PEP教材习题形式多样．如“练习”、“习题”、“复习参考题”等．练习题是对所学知识和例题的进一步深化，起到练习的作用；习题一般位于某一大节之后，起到巩固和综合的作用，一般是根据相关度较高的知识点模块分为A组和B组两类，B组习题难度大于A组习题；复习参考题位于章节最后，题量较大，一般也分为A组和B组，B组习题难度也大于A组，主要是考查学生对整章知识的掌握程度．另外，还有在教材正文中以“观察”、“思考”、“探究”、“讨论”等形式呈现的问题．

UCSMP教材一般是每节后习题、自我测试题和每章末尾的总复习参考题．章节后习题主要分为4个部分：巩固类题（Covering the reading）、应用类题（Applying the Mathematics）、复习类题（Review）、探索类题（Exploration）．巩固类题主要是覆盖教材内容的一些基本题，通过做这类题让学生掌握教材中所述的一些基本的数学概念、公式及定理；应用类题是把所学到的数学内容应用到具体的实例中去；复习问题主要是一些综合性题目，让学生加深对所学内容的理解，不仅包括本章所学内容，通常还包括对之前各章所学知识的巩固应用；探索类题是一些多解性或开放性的题目，有些还需要学生自己动手收集数据，加以分析并设计解题方案，这显然是UCSMP教材习题呈现的一大特色．每一章之后，UCSMP教材还有一个自我测试题（Progress Self-Test），题量适中，之后就是一个章末复习题（Chapter Review），题量较大，分为4个部分：技能检测题（Skills）、性质检测题（Properties）、应用检测题（Uses）、表达检测题（Representations）．每部分的题量都较适中，均涵盖了本章中的基本内容和重难点知识，从4个部分分层次来考查学生对知识的掌握情况．另外，UCSMP教材每小节习题中的每一题都在题目后用小括号注明所用的知识在哪一章节，章末复习题中每个部分也是分别设置各个小目标，比如技能检测题中设目标A、B、C、D（Object A、Object B、Object C、Object D），每个目标都注明了涉及的知识在哪个章节．

总的来说，UCSMP教材的习题呈现方式是比较完善的，教材对习题进行细化分层，并进行弹性处理．另外，习题难度呈现阶梯状，体现了不同层次学生的选择，为学生提供更多的选择空间．由此可见，UCSMP教材在习题的呈现方式上要比PEP教材更具有多样性．

3.2 习题数量

两版教材平面向量的习题数量统计情况如表3所示．在习题数量方面，PEP教材在这一章中设置的总习题数量为140道，平均每节为28道；UCSMP教材为135道，每节为34道，两版教材习题的数量分布差异不显著（χ2（1, N=337）=0.461，p>0.1）．两套教材都设置了较多的习题，均重视习题训练对学生学习知识和方法的作用．PEP教材在每节后习题训练的安排上相对较少，一共是63道，占45%，而UCSMP教材在每节后习题数量为84道，所占比例为62.2%，但是PEP教材中“练习”部分的习题要求在课堂当中完成．PEP教材中习题部分A组的题目要远远多于B组，强调基础性原则．UCSMP教材巩固类题（Covering the reading）所占的题目最多，这部分类似于PEP教材中的习题A组，学生通过课前预习、教师讲解之后，大多都可以独立完成此类题目，题量占其次的是复习类题．最后，PEP教材、UCSMP教材中的章末复习题所占比例分别为26.4%、29.6%，数量相差不多．

表3 两版教材“平面向量”习题数量比较

3.3 习题类型

两个版本平面向量习题类型统计具体情况如图1所示：

图1 两版教材习题类型折线图

从统计数据来看，在习题的类型上，两版教材题型都较丰富，两版教材习题类型分布有显著差异（χ2（5, N=275）=23.22，p<0.001），其中选择题、填空题、判断题等题型两版教材配置的题量都较少，特别是UCSMP教材的填空题为0道，选择题只有2道，而且还是多项选择题，判断题也只有1道．PEP教材这3者类型的题目数量要更多，选择题、填空题、判断题所占比例分别为9.3%、2.9%、5.7%，但PEP教材的选择题基本只出现在章末复习题，判断题也是相似的情形．两个版本的教材中，比例最高的仍然是传统题型解答题，PEP教材和UCSMP教材解答题各占习题总量的比例分别为60%、69.6%，由此可见，UCSMP教材解答题数量多于PEP教材；其次是作图题和证明题，PEP教材和UCSMP教材证明题所占比例为11.4%、7.4%，作图题所占比例为10.7%、20.7%．因此，证明题数量PEP教材比UCSMP教材多，作图题的比例PEP教材要比UCSMP教材少10%．向量作为连接代数和几何的工具，其图形属性不容忽视．

3.4 习题认知水平

根据以上数学认知水平分析框架，对两版教材平面向量的习题进行统计分析，具体如表4所示：

表4 两版教材“平面向量”习题认知水平比较

从上表可知，两版教材习题认知水平分布有显著差异（χ2（3, N=275）=16.01，p<0.01）．水平1：计算——操作性记忆水平两版教材题目数量所占比例相似，说明两版教材的习题与例题匹配程度较高，学生可以参照例题、模仿例题进行解答．水平2：概念——概念性记忆水平的题目，PEP教材的题目要比UCSMP教材高18.7%．把水平1和水平2的题目合计，PEP教材中记忆水平（较低认知水平）的习题占65.7%，UCSMP教材记忆水平的习题占41.8%，比PEP教材低23.9%．水平3：领会——说明性理解水平的题目，UCSMP教材要比UCSMP教材高4.8%．水平4：分析——探究性理解水平的题目比例相差较大，UCSMP教材要比UCSMP教材高7.1%．水平3和水平4题目合计，PEP教材中理解水平（较高认知水平）的习题比UCSMP教材低23.9%．整体来看，PEP教材记忆水平的习题明显多于UCSMP教材，主要是PEP教材水平2的习题明显多于UCSMP教材，水平4的习题明显少于UCSMP教材．

3.5 习题难度

以下对两版教材平面向量部分的习题难度进行分析，为此，先根据表1中的水平划分，对两版教材中的习题逐一进行鉴定，并利用公式（*）计算每个难度因素的加权平均，其结果如表5所示．

由统计数据可知，在五个因素方面两版教材具有显著性差异（χ2（4, N=17）=15.56，p<0.01），具体分析如下：

（1）探究因素方面，两版教材具有显著性差异（χ2（2, N=275）=9.231，p<0.01）．PEP较注重“识记”，所占比例高达41.4%，比UCSMP教材高12.5%，体现了PEP教材抓基础的特性，UCSMP教材却更专注于“理解”和“探究”层次，“理解”层次所占比例要比PEP教材高3.5%，“探究”层次所占比例要比PEP教材高9%．另外，两版教材的加权平均之后的难度值也相差0.21，由于UCSMP教材知识呈现以问题为载体，以问题解决为导向，因此习题中探究因素难度相比于PEP教材要大一些．

（2）背景因素方面，两版教材具有显著性差异（χ2（3, N=275）=33.022，p<0.001）．PEP教材中没有实际背景的例习题要比UCSMP教材高出13.7%，而PEP教材涉及“个人生活”的习题占2.8%，UCSMP教材中涉及这方面的习题占9.6%，另外，UCSMP教材在涉及“公共常识”和“科学情境”的习题所占比例也大于PEP教材．由此可见，UCSMP教材中的习题更关注与学生的个人生活和公共生活方面的联系，而PEP教材在这方面相对来说比较薄弱．

（3）运算因素方面，两版教材差异不显著（χ2（3, N=275）=1.098，p>0.5）．学生运算能力的培养主要体现在“简单符号运算”水平，其中“复杂符号运算”水平层次，两版教材的习题所占比例均比较低，分别为10.0%、14.1%，相对来说UCSMP教材中在复杂符号运算水平要高4.1%，其中很大一部分原因在于复习题中涉及了之前所学的知识．两版教材运算因素方面的难度水平相差不大，这也说明两版教材注重的都是基本运算的掌握，而弱化了对复杂运算的要求．

（4）推理因素方面，两版教材差异不显著（χ2（3, N=275）=2.454，p>0.25）．占比例较多的都是“无推理”水平，PEP教材所占比例为55.7%，UCSMP教材所占比例为46.7%．一方面是因为“平面向量”知识学生刚接触，所以涉及到的“复杂推理”并不是很多；另一方面是两版教材当中计算题和作图题多一些，导致无推理题占的比例相对多一些．相对UCSMP教材来说，PEP教材中的习题在推理方面明显比UCSMP教材的要简单一些．主要是UCSMP教材比较注重知识的探究应用以及学生的数学能力的培养，特别是学生解决数学问题的能力，所以设置较多的“探索题”和“推理题”．

（5）知识含量方面，两版教材具有显著性差异（χ2（2, N=275）=6.022，p<0.05）．两版教材均在“单个知识点”方面所占比例最高，其次是“两个知识点”方面．由于“平面向量”的知识学生刚接触，PEP教材更多的是落实基础性原则，所以在这方面的难度要略小于UCSMP教材．UCSMP教材在这方面难度更大主要是因为其教材每章节后面的“复习类题”当中的题目综合性都比较强，这些题都是对前面所学内容的巩固和应用，有时还会与本小节知识综合考查学生的掌握程度．

总体来说，UCSMP教材难度要大于PEP教材，部分习题难度较大，综合性强，需要学生具有良好的基础和较强的数学思维能力．而PEP教材在习题方面坚持以基础题为主、中档题为辅、适当涉及难度较大的综合题和开放题，在保证问题数量的同时更要保证问题的质量．

表5 习题难度的比较

4 启 示

4.1 适当丰富习题呈现方式

习题既是知识的应用，又是知识和能力的再生．习题的设置在很大程度上会影响学生对数学知识的理解及其数学思维的形成过程[9]．PEP教材虽然对习题进行了分层次处理，但没有根据不同的知识技能目标，进行更加细致具体的分层处理．UCSMP教材的节习题分为“巩固题”、“应用题”、“复习题”、“探索题”等，对章复习题又以“技能”、“性质”、“应用”、“表达”4个方面分层次呈现，具有较完善的习题呈现方式，还根据各个层次的不同目标具体分配数量不同的习题．在教材编写中，中国教材应该结合向量知识内容的特点，在保持层次性、重基础等特色的同时，可参考UCSMP教材当中的习题呈现方式，根据不同的目标对习题更加细化分层，在节习题的设置上尽量涵盖知识技能、理解应用、巩固复习、探究拓展等目标的习题，增加习题的层次感和目的性．

4.2 提高较高认知水平习题比例增加探索性和开放性习题

根据以上研究发现，PEP教材安排了较多处于水平2——概念性记忆水平的题目，说明中国教材对主要概念、公式、定理等给予了充分重视，但UCSMP教材较高认知水平（水平3和水平4）的习题比例要远多于PEP教材，习题形式也更丰富．水平3和水平4的习题要求学生在掌握概念、定理等知识的基础上解决一些更复杂的问题，尤其是水平4——探究性理解水平的习题，学生需要根据不同的问题情境，创造性地解决一些非常规的问题．PEP教材需要在注重双基、重视概念练习的前提下，学习借鉴UCSMP教材习题重视较高数学认知水平的培养，降低与例题形式完全相同、直接模仿例题解答的练习题比例，提高较高认知水平练习题，重视向量知识与其他数学领域知识联系的做法，设置多样化的习题，给学生提供一些非常规问题、开放题（结论开放或过程开放）、探索题等．由于“探索题”和“开放题”不一定有唯一的解法和结论，这就有助于培养学生的观察、分析、综合、类比、归纳、猜想等综合解决问题的能力，数学教材中设置这样一些习题就能够更有效地引导和组织学生在经历观察、实验、比较、分析、抽象概况等活动中，在相互合作交流中，对现实生活中蕴含的数学模式进行思考和交流，不断提高学生用数学解决实际问题的能力，培养学生的创新能力和提出猜想、构造模型、推理证明并一般化等高水平数学能力[7]．

4.3 注重习题背景的多样化紧密联系生活实际

《普通高中数学课程标准（实验）》指出：高中数学课程应力求使学生体验数学在解决实际问题中的作用、数学与日常生活及其他学科的联系，促进学生逐步形成和发展数学应用意识并提高实践能力．新课程理念强调要把数学与现实生活相联系，特别是与学生的个人生活相联系，帮助学生学会“有用的数学”[9]．相对来说，PEP教材习题的选材与现实生活联系的比较少，习题基本上都是纯数学问题，较少有生活情景．而UCSMP教材中的习题背景涉及科学、经济、物理、生物、化学、营养学等各个学科内容的相关知识，而且注重与学生的实际生活经验相联系．空洞的数字符号是不会容易让学生产生兴趣的，在教材编写中应尽量让习题选材密切联系生活实际，特别是重视联系学生个人的生活实际，创设更多的与学生息息相关的问题情境．设计富有挑战性和趣味性的活动，使学生有更多的机会从周围熟悉的事物中学习数学和理解数学，在认识、学习和应用数学知识的过程中，感受数学与生活实际的密切联系．尽管PEP教材将平面向量的应用及与其他章节或学科的交叉部分置于同一节中，统一向学生介绍，这些应用涉及的更多是与物理相关的问题，但这远远不够[10]．

总之，对比中美高中数学教材中的习题，可以发现美国数学教育中许多新的理念已经渗透到UCSMP教材中．中国数学教材的编写应当认真研究这些教材的特色、特点，将美国成功的做法吸收到新教材中．当然，这种吸收不是简单的抄袭，而是合理的吸收[11]．

[1] 孙晓天．近年来我国中小学数学教材建设述要[J]．数学教育学报，2008，17（4）：6-10．

[2] 叶立军，王晓楠．中美高中数学教材比较研究[J]．数学教育学报，2012，21（2）：49-52．

[3] 王申怀．美国UCSMP教材（第六册）介绍[J]．数学教育学报，1997，6（1）：66-70．

[4] 章建跃．普通高中课程标准实验教材数学（选修2-2）[M]．北京：人民教育出版社，2007．

[5] UCSMP. Precalculus and Discrete Mathematics [M]. Chicago: The McGraw Hill Companies, 2010．

[6] 沈兰，郑润洲．变革的见证：顾泠沅与青浦教学实验年[M]．上海：上海教育出版社，2008．

[7] 高文君，鲍建生．中美教材习题的数学认知水平比较[J]．数学教育学报，2009，18（4）：57-60．

[8] 鲍建生．中英两国初中数学期望课程综合难度的比较[J]．全球教育展望，2002，（9）：48-52．

[9] 张笑谦，胡典顺．中澳高中数学教材的比较及启示[J]．数学教育学报，2013，22（2）：71-75．

[10] 张笑谦，胡典顺．澳大利亚VCE课程与PEP高中数学教材平面向量章节的比较与思考[J]．数学通报，2013，（10）：22-27．

[11] 李善良．论中小学数学教材编写的基本原则[J]．数学教育学报，2007，16（1）：70-73．

Comparative Study on Exercises of Chinese and American Mathematical Teaching Materials——A Case Study of Plane Vector Chapters from Chinese PEP Edition High School and American UCSMP Edition Teaching Materials

LIN Dan, HU Dian-shun
(School of Mathematics and Statistics, Central China Normal University, Hubei Wuhan 430079, China)

The reconstruction of teaching materials is an important mark of a new round of China’s reform of the mathematical curriculum, which also concretely represents the requirement and principle of the reform. By contrast of exercises of plane vector chapters from Chinese PEP edition high school and American UCSMP edition teaching materials, it can be found that the exercises from UCSMP edition textbooks are represented in various ways and redacted in different levels, are more closely connected to life and the cultivation of higher cognitive level, more open and thought-provoking, whereas are also more difficult. While the exercises from Chinese PEP edition high school textbooks are abundant in types, but not abundant in higher cognitive level, which makes them better from the perspective of difficulty. However, it shows an inadequacy of open and thought-provoking questions. In the compiling of teaching materials, PEP may consider to enrich the ways of presentation, improve the proportion of exercises of the higher cognitive level, add more exploratory questions, pay attention to the diversity of background of exercises and strengthen their connection to life.

contrast of mathematical teaching materials; plane vector; exercises; enlightenment

G40-059.3

：A

：1004–9894（2015）03–0063–05

[责任编校：张楠]

2015–01–20

湖北省教学研究项目——数学师范生拔尖创新人才培养的理论与实践（2013090）；中央高校基本科研业务费专项资金资助——数学问题提出与数学教育改革：跨国比较研究（CCNU13F021）；华中师范大学研究生教学改革研究项目——免费师范生攻读教育硕士培养模式的改革研究与实践（2013JG18）；华中师范大学教师教育学院研究专项资助（2012JS07）；湖北省教育科学“十二五”规划2013年度立项课题——数学问题提出与数学教育改革：跨国比较研究（2013B015）

林丹（1991—），女，江西赣州人，硕士，主要从事数学课程和教学论的研究．胡典顺为本文通讯作者．