概念图在评价数学概念性理解中的应用

金海月

（南京师范大学 教师教育学院，江苏 南京 210097）

概念图在评价数学概念性理解中的应用

金海月

（南京师范大学 教师教育学院，江苏 南京 210097）

概念图能够从概念间的相互关系以及知识组织结构等角度提供有关概念性理解的丰富信息．采用社会网络分析法对概念图进行数据处理，并对比分析概念图与传统评价方式在评价数学概念性理解上的异同，可以为相关数学概念的教学提供有价值的信息；对概念图作为评价工具的应用性研究也将为新课程所倡导的发展性评价方式的探索与实践提供参考．

概念性理解；初中数学；评价；概念图；社会网络分析法

概念性理解是数学教育的一个重要目标．关于数学学习的教育心理学研究充分肯定了概念性理解在数学学习中的重要性，认为概念性理解是学生灵活运用知识及在不同背景条件下恰当应用知识的前提条件[1]．教育工作者们在评价学生的概念性理解水平上投注了大量精力[2～5]．在众多方法中，概念图被认为是一种有效的评价方式，它能够从概念间的相互关系以及知识组织结构等角度提供有关概念性理解的丰富信息[6～8]，并能在评价过程中促进学生对知识的整合．国内关于概念图在评价学生数学概念性理解方面的实证研究较少，且现有的概念图分析方法没有充分发挥其图式表征的优势．下面的研究将致力于探讨以下两部分内容：（1）结合概念图及传统评价方式了解学生数学概念性理解的现状；（2）采用社会网络分析这一跨学科的方法对概念图进行数据处理，并对比分析概念图与传统评价方式的异同．

1 核心概念

1.1 概念性理解

教育研究者们用概念性理解（Conceptual Understanding）来强调某知识领域概念间的关系，其表征一般为有联系的层次网络结构．Kilpatrick等人将数学中的概念性理解定义为“对数学概念、应用及关系的掌握”[9]．结合R. Skemp对数学概念形成的层次结构的刻画[10]以及认知心理学领域对数学理解和概念性知识（Conceptual Knowledge）的描述[11～13]，将数学概念性理解细分为3个维度：① 单个概念：包括定义、例和反例以及不同的表征形式；② 概念间的相互联系：包括等值抽象、弱抽象、强抽象和广义抽象等逻辑关系，还包括包含、归类、变换、类比等本体论关系；③ 应用：侧重指对概念及其关系应用的原理性认识，不包括操作层面的程序性知识．

1.2 概 念 图

概念图指由J. D. Novak等人基于有意义学习理论开发的一种能形象刻画某知识领域中概念及其关系的图解[14]．在概念图中，结点对应着代表各种概念的重要术语名词，连线代表一对概念之间的关系，连线上的连接词则表示该连线具何种关系，两个结点与一个带连接词的连线共同构成一个命题．概念图能够有效地刻画学生头脑中的知识组织结构，它区别于其他评价方式的一个重要特征是其外显的图式结构．但现有的概念图分析方法局限于对其中结点、连线、命题和整体结构的定性描述以及定量打分[15]，没有充分发挥概念图的图式表征优势．下面将借助社会网络分析法对概念图作进一步分析．

1.3 社会网络分析法（Social Network Analysis，简称SNA）SNA是社会学中的一种研究方法，一般用以研究社会实体间的关系以及这些关系的模式和含义[16]．例如，用网络观点来充分理解和模拟公司间的业务往来，分析个体的受欢迎程度、影响、派系等．将社会实体间的网络关系研究类推到数学概念领域，可以从学生认知角度研究概念的核心程度，不同概念间的从属结构、紧密关系等．

2 理论基础

关于数学概念学习的心理学研究中具有代表性的是R. Skemp的数学概念形成的层次结构模型[10]和喻平的CPFS结构理论[17～18]．R. Skemp将数学概念分为初等概念（primary concept）和高层次概念（higher-order concept）．初等概念指能够从直接经验中获得的概念，如自然数；高层次概念指在概念关系或一组概念共有特性基础上抽象出来的概念，如质数．除了初等概念，所有的数学概念都是在其他概念的基础上抽象出来的，概念的形成过程决定了数学概念间的逻辑层次关系，这也是数学课程设计的主要依据．喻平的CPFS结构理论依据概念间的等价或抽象关系提出概念域和概念系的概念．概念域指某个概念的一些等价定义在学习头脑中形成的知识网络，概念系是指一组有着直接或间接抽象关系的概念在学习者头脑中形成的概念网络．类似的还有命题域和命题系．概念域、概念系、命题域和命题系一起简称为CPFS结构．二者的共同之处是认为数学概念（知识）是按层次网络形式组织的．R. Skemp是从数学概念形成的客观历程角度对概念间的层次关系进行阐述；喻平的CPFS结构理论是从学习心理学的角度出发，认为学习者需要从多角度，在多背景下深入理解概念，在头脑中形成完善的概念体系，才能及时、有效地调用适当的模式去解决问题．R. Skemp的数学概念形成的层次结构模型和喻平的CPFS结构理论为概念图在评价数学概念性理解的应用提供了理论基础．

3 国内外研究现状

关于概念图在评价概念性理解方面的应用，国外的研究主要集中在科学领域，例如物理、生物．研究者们利用概念图探测学生的概念理解情况以及跟踪学生头脑中概念体系的发展（如文[19～20]）．国内有关概念图的研究则主要是对国外文献的综述，缺乏实证性研究．尽管在数学领域的此类研究相对较少，概念图的相关理论和研究方法同样适用于评价数学概念性理解．Mansfield等人利用概念图调查了澳大利亚几个小学的学生关于平面图形相关概念的理解情况[21～22]．他们认为概念图能够有效地反映学生概念性理解中的知识缺失和理解性错误，并且在构建概念图的过程中，学生有机会反思概念间的联系，从而加深对相关概念的理解．Afamasaga-Fuata’I在其编著的《数学中的概念图：从研究到实践》[23]一书中介绍了多个利用概念图评价学习者数学概念发展的个案研究．研究显示概念图能够很好地刻画学习者不同阶段的概念性理解情况，同时，也能够反映不同学习者在概念性理解上的特征和差异．

现有研究中对概念图的定量分析主要沿用了Novak的方法，即依据概念图的概念、命题、分支、交叉连接和层级结构这几个方面进行定量打分．此类定量打分的方法使得概念图能够应用在大规模的终结性评价中，但是它极大地限制了概念图的图式优势；仅凭分数，尤其是累积分，很难反映出学生的概念性理解情况[24]．因此，部分研究者倾向于对概念图作定性描述．但定性描述很难同时处理较多学生的概念图．鉴于以上考虑，研究采用定量与定性相结合的方式，同时借助跨学科的社会网络分析法对概念图进行分析．

4 研究方法

研究旨在考查概念图在评价数学概念性理解方面的应用，了解学生数学概念性理解的现状．

4.1 研究对象

研究采用便利取样的方法选取了江苏省某初级中学二年级的一个班级，共计48名学生作为被试．在调查之前，先对被试进行了详细的概念图构图培训，旨在让他们了解概念图的定义和基本用途，并能够掌握构建有意义的概念图的步骤及方法．培训之后，对被试的概念图构图技能进行测验，结果显示被试已基本掌握培训内容，具备构建有意义概念图的能力．

4.2 研究材料

概念性理解的测试材料由3类测试卷组成：概念定义测试卷、概念构图测试卷以及传统题卷．概念定义测试卷以表格的形式呈现，要求学生写出所给数学概念的定义，并举例及反例．概念构图测试卷要求学生用所给的10个核心概念构建一个概念图，呈现所给概念间的相互关系．该测试卷包括两条提示语：（1）请尽可能多地构建概念间的有意义连接；（2）请尽可能使用完整准确的连接词．传统题卷则以传统考试题的形式侧重考查学生对相关数学概念及其应用的掌握情况．

4.3 数据收集

概念定义测试卷和概念构图测试卷是一起施测的，给时45分钟．首先要求被试在15分钟内完成概念定义测试卷；之后是概念构图测试卷，要求被试就概念定义测试卷中所给概念构建一个概念图．传统题卷则安排在上述测试的第二天，要求被试在45分钟内完成．

4.4 数据分析

研究采用两种方法对学生构建的概念图进行分析．一种是源于Novak的传统分析法：有效命题赋值计分，所有命题得分的总和即为概念图的命题得分．另一种是社会网络分析法，主要考虑单个概念的出度、入度，成对概念的连线情况，以及整体概念图的组织结构．例如，图1中A、B、C、D、E共计5个概念，从概念A出发有两条连线（A→B及A→D），但图中没有连线指向A；因此，A的出度为2，入度为0. 概念E与另4个概念之间没有连线，因此，E的出度和入度均为0. 在学生构建的概念图中，若某概念的出度和入度均为0，则表示学生不能有效地建立它与其他相关概念之间的联系，也即意味着学生对该概念的理解有所欠缺．

表1是上述A、B、C、D、E 5个概念的出度和入度情况统计；表2是图1中成对概念的关联情况．若A、C两个概念间的关系是重要且需要学生掌握的（例如，等腰三角形和等边三角形），但表2中“从A到C”或“从C到A”对应数据均为0，则表示学生不熟悉或没有掌握这两个概念间的关系．

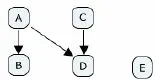
图1 概念图举例

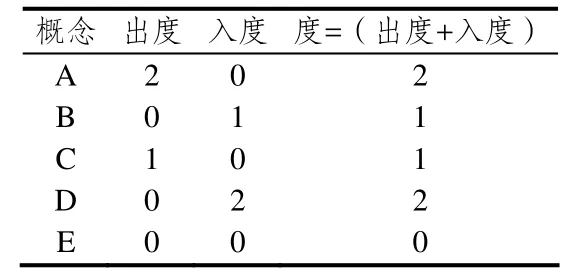
表1 概念的出度、入度和度

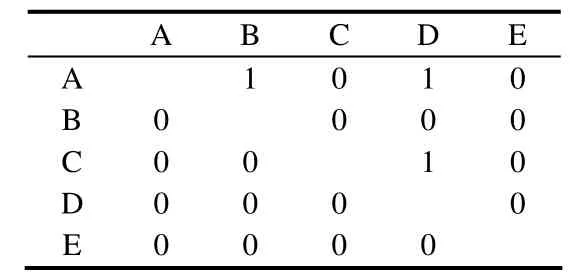
表2 成对概念的关联情况

图1所示的概念图中的连线数为3（包括A→B、A→D及C→D），相关概念数为5（A、B、C、D、E），该图的密度则为3/5=0.6．密度与Novak的有效命题得分是刻画概念图整体属性的不同指标，二者相关但不等同．

综合Novak的传统分析法以及社会网络分析法可以更好地刻画概念图的相关属性，详见表3．

概念定义测试卷和传统题卷的评分相对比较直接．

概念定义测试卷中每个正确定义给2分，部分正确的定义给1分，错误0分；正确的例子给2分，错误的0分；正确的反例2分，错误0分．因此，概念定义测试卷的满分为(2+2+2)×10=60．

传统题卷的满分为100分，题型包括判断题、选择题、填空题和简答题几种类型，各种题型的给分及分布都较为接近于传统试题．

表3 概念图分析方法

5 研究结果与讨论

5.1 单个概念

表4中的概念按照总连线数由大到小降序排列．其中“可接受命题比”的计算如下：设T为总连线数（忽略箭头方向），C为标注正确连接词的连线数，P为标注部分正确连接词的连线数，则“可接受命题比”=(2C+P)/2T，反映了学生对某概念相关关系理解的正确程度．

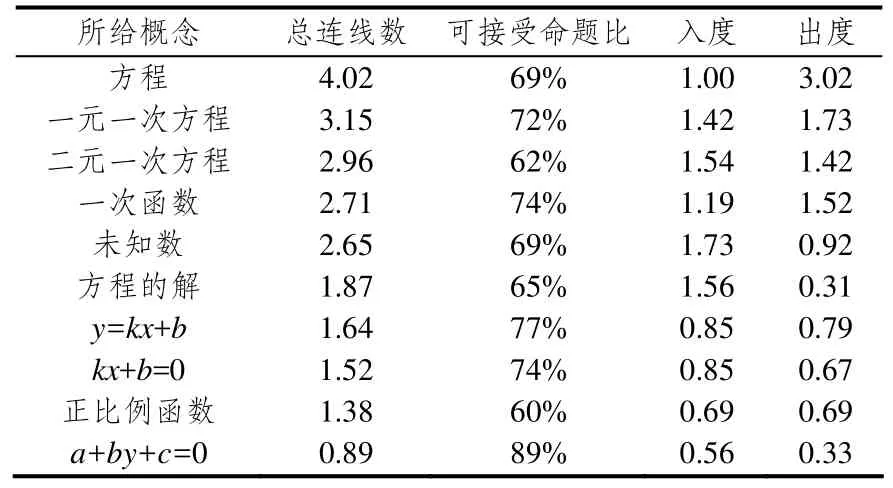
表4 单个概念的连线均值

“方程”作为这10个概念的总括性概念，学生最易于从“方程”出发联想到其他相关概念（出度3.02）．通过对比发现，“一元一次方程”、“二元一次方程”和“一次函数”的平均总连线数都高于它们对应的符号表征“kx+b=0”，“ax+by+c=0”和“y=kx+b ”．例如“二元一次方程”总连线数为2.96，而“ax+by+c=0”的总连线数仅为0.89．一方面，可能是学生更为熟悉这3个概念的文字表征；另一方面，由于所给的10个概念中，仅有3个是概念的符号表征，其余7个均为文字表征，学生可能更易于在相同表征间建立联系．

表4中10个概念的可接受命题比介于60%（正比例函数）和89%（ax+by+c=0）之间，略低于预期．除了对概念的错误理解外，学生在连线上标注的不完整或仅部分正确的连接词也是导致较低分值的一个原因．例如，学生在概念图中仅标注“（正比例函数）是一种特殊的（一次函数）”，按照评分标准，这样的命题属于“部分正确”赋值1分，应说明如何特殊，如“（正比例函数）是图像经过坐标原点的一类（一次函数）”．在前期概念构图培训中，已对培训者强调要用详细完整的连接词标注关系，否则在评分时视作对概念关系理解不深刻．

5.2 成对概念

表5中每对概念所对应的单元格中有两个数字，以斜线隔开．斜线前的数字代表所建连接总数，斜线后的数字代表所建连接中连接词标注正确或部分正确的连线数．以从“一元一次方程”到“一次函数”的连线情况为例：12/7表示在48名学生的概念图中，有12名学生画出了从“一元一次方程”到“一次函数”的连线，其中7名学生在连线上标注了正确或部分正确的连接词．由于在培训中已强调连接词的必要性，学生概念图中的所有连线都有标注，因此12-7=5即为标注错误连接词的连线数．

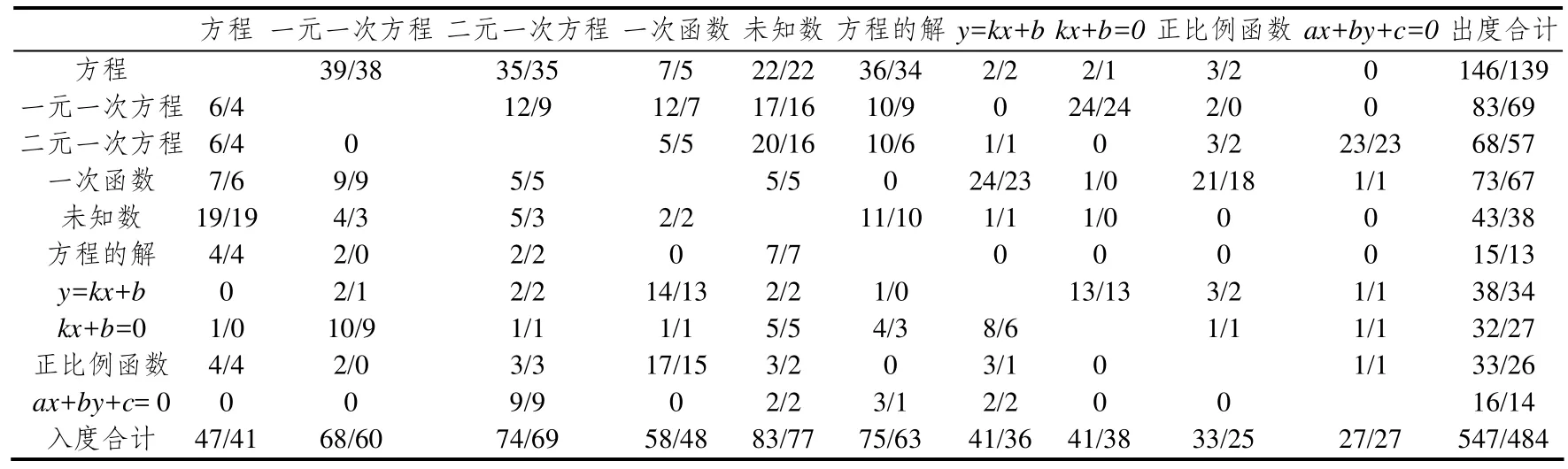
表5 成对概念的连线情况

表格的最后一行是各概念的入度合计，斜线前的数值除以学生数48即为表4中对应概念的入度．同样，表中最后一列是各概念的出度合计，斜线前的数值除以48即为表4中对应概念的出度．表5右下角的547/479则表示48名学生建立的547条连线中，有484条标注了正确或部分正确的连接词，547-484=63条连线标注了错误连接词．通过表格中斜线前后的数字对比能在一定程度上获知学生对某概念或某关系的熟识程度和掌握情况．

如表5所示，有50%左右的学生能够较为正确地建立“一元一次方程”“二元一次方程”与它们相应表达式之间的联系，但是在它们与其它概念的联系中出现了或多或少的错误．例如，从“二元一次方程”到“未知数”的连线总数为20，但有4个的连接词标注错误．学生将“二元一次方程”与“一元二次方程”混淆，认为“二元一次方程”中只有一个未知数且未知数的次数为2．在构建概念图时，学生需要用自己的语言来描述概念间的关系．因此，通过学生构建的概念图，研究者能收集到传统测试中不常发现的概念性错误．

5.3 聚合概念图（Collective Map）

聚合概念图是在表4和表5数据的基础上构造出的．图中各概念的位置由研究者参照教材中体现出的各概念的数学逻辑层次安排，自上而下，由一般到特殊，整体到部分．

图中代表概念的圆圈大小依据表4中对应概念的总连线数而定，总连线数越多，圆圈越大；代表连线的→分为粗线、细线和虚线3类．粗线表示超过50%的学生都建立了该联系，属强连接；细线代表少于50%但多于25%的学生建立了该联系，属中度连接；而虚线则表示少于25%的学生建立了该联系，属弱连接．

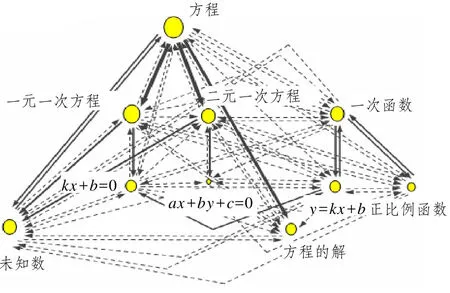
图2 聚合概念图（Collective Map）

如图2所示，图中仅有3条粗线标注的连线，大部分连线为细线或虚线，表示学生对所给概念的组织方式存在差异，交集较少．3条粗线和多数细线的方向都是自上而下，反映了学生习惯于由一般概念联系到特殊概念，或是由整体联想到部分．所给的10个概念被大致分为了左右两个子群，右侧子群中的一次函数、正比例函数以及y=kx+b与概念图中其他概念的联系较弱．两个子群的联系主要是通过“y=kx +b ”以及“kx+b=0”建立的，例如有学生标注“kx+b=0的解是y=kx+b与x轴交点的坐标”．研究者没有采用教材中常见的表达式“ax+b=0”也是为了与一次函数表达式“y=kx+b”更为接近，进而暗示学生二者关系的存在．尽管如此，大多数学生还是不能建立起方程与函数的有意义联系．该弱连接提醒教师在教学中需加强干预，帮助学生建立方程和函数间的有效联系，以便于他们更好地理解抽象的函数概念．将同样的方法应用于其他数学知识领域，获知学生头脑中概念组织规律或是认知结构中存在的缺陷，亦能为教材编制者提供信息，以便他们有针对性地改善教材．

5.4 三类测试卷的相关性分析

概念定义测试卷、概念构图测试卷以及传统题卷都检测了学生数学概念性理解的一个或多个侧面．概念图得分与概念定义测试卷和传统题卷的得分均呈显著性相关，并且概念图的命题得分与概念定义测试卷和传统题卷的相关性明显高于概念图的密度与它们的相关性，说明与密度相比，概念图的命题得分能够更好地反映学生概念图的质量．由于概念定义测试卷中，学生举例及反例时的正确率较高，不能有效地区分学生对概念的理解情况，概念图与这两者的相关系数相对较低，介于0.382～0.582之间．

表6 三类测试卷的相关性分析（Spearman系数）

6 总 结

概念定义测试、概念构图测试以及传统题3类试题在评价数学概念性理解上各有优势．概念图所揭示的学生的概念性理解现状与另两类测试存在交集，但亦有不同．例如，概念图中的一些连接词是概念的定义，这是与概念定义测试卷相通的部分．但是，在概念图中，学生很少提及相关概念的例或反例，也不涉及概念在解题中的应用；而概念图所反映出的学生对概念的一些错误理解以及概念的组织结构是其他非开放性测试所不能揭示的．概念图在评价数学概念性理解上优势凸显的同时，研究结果也发现学生会在概念构图时规避一些自己不熟悉或不确定的内容，因此，概念图也存在局限性，它不能全面地揭示学生对某领域内相关概念联系的理解．结合不同类型的测试有助于教育研究者获得有关学生概念性理解的更为完整的信息．

[1] Bransford J D, Brown A L, Cocking R R. How People Learn: Brain, Mind, Experience, and School [M]. Washington, DC: National Academy Press, 1999.

[2] Castellón L B, Burr, Kitchen R S. English Language Learners’ Conceptual Understanding of Fractions [A]. In: K Téllez, J Moschkovich, M Civil. Latinos/as and Mathematics Education: Research on Learning and Teaching in Classroomsand Communities [C]. Charlotte, NC: Information Age, 2011.

[3] Niemi D. Assessing Conceptual Understanding in Mathematics: Representations, Problem Solutions, Justifications, and Explanations [J]. The Journal of Educational Research, 1996, 89(6): 351–363.

[4] 高雪芬，鲍建生．大学生对微分概念的理解及认知方式分析[J]．数学教育学报，2013，22（1）：40–43．

[5] 李善良．关于数学概念表征层次的研究[J]．数学教育学报，2005，14（4）：35–37．

[6] Novak J D. The Development of the Concept Mapping Tool and the Evolution of a New Model for Education: Implications for Mathematics Education [J]. Focus on Learning Problems in Mathematics, 2006, 28 (3–4): 3–31.

[7] White R T, Gunstone R. Probing understanding [M]. Philadelphia, PA: The Falmer Press, 1992.

[8] 王兄，汤服成．概念图及其在数学学习中的现实意义[J]．数学教育学报，2004，13（3）：16–18．

[9] Kilpatrick J, Swafford J, Findell B. Adding it up: Helping Children Learn Mathematics [M]. Washington, DC: National Academic Press, 2001.

[10] Skemp R. The Psychology of learning Mathematics [M]. Middlesex, UK: Penguin Books, 1971, 1986.

[11] Hiebert J, Lefevre P. Conceptual and Procedural Knowledge in Mathematics: An Introductory Analysis [A]. In: J Hiebert. Conceptual and Procedural Knowledge: The Case of Mathematics [C]. Hillsdale, NJ: Lawrence Erlbaum Associates, 1986.

[12] Piaget J. The Development of Thought: Equilibration of Cognitive Structures [M]. New York, NY: Viking Press, 1977.

[13] Skemp R. Relational Understanding and Instrumental Understanding [J]. Arithmetic Teacher, 1976, 26(3): 9–15.

[14] Novak J D, Gowin D B. Learning How to Learn [M]. Cambridge, London: Cambridge University Press, 1984.

[15] 刘荣玄，罗贤强，徐向阳．关于概念图在数学教学评价中的应用研究问题[J]．数学教育学报，2011，20（4）：51–54．

[16] Wasserman S, Faust K. Social network analysis: Methods and applications [M]. New York: Cambridge University Press, 1994.

[17] 李渺．试论个体CPFS结构与数学理解的关系[J]．数学教育学报，2006，15（4）：29–32．

[18] 喻平，单墫．数学学习心理的CPFS结构理论[J]．数学教育学报，2003，12（1）：12–16．

[19] Hough S, O’Rode N, Terman N. Using Concept Maps to Assess Change in Teachers’ Understanding of Algebra: A Respectful Approach [J]. Journal of Mathematics Teacher Education, 2007, (10): 23–41.

[20] Williams C G. Using concept maps to determine differences in the concept image of function held by students in reform and traditional calculus classes [D]. Berkeley: University of California, 1994.

[21] Mansfield H, Happs J. Using Concept Maps to Explore Students’ Understanding in Geometry [N]. Paper Presented at the Thirteenth Annual Conference of the International Group for the Psychology of Mathematics Education, Paris, 1989.

[22] Mansfield H, Happs J. Concept maps. [J]. The Australian Mathematics Teacher, 1991, 47(3): 30–33.

[23] Afamasaga-Fuata’I K. Concept Mapping in Mathematics: Research into Practice [M]. New York, NY: Springer, 2009.

[24] Kinchin J M, Hay D B. How a Qualitative Approach to Concept Map Analysis Can Be Used to Aid Learning by Illustrating Patterns of Conceptual Development [J]. Educational Research, 2000, (42): 43–57.

Using Concept Map to Assess Conceptual Understanding in Mathematics

JIN Hai-yue
(College of Teacher Education, Nanjing Normal University, Jiangsu Nanjing 210097, China)

Concept map is a viable assessment technique that can provide rich information about students’ conceptual understanding especially about the connections between concepts and their organizational structure. This study employed a method，termed Social Network Analysis, from social science for analyzing student-constructed concept map and compared concept map with traditional measurements of conceptual understanding. The findings from this study about students’ conceptual understanding of certain mathematical concepts would provide research-based information for teaching. The use of concept map as an assessment technique would also be useful reference for the exploration of developmental evaluations in mathematics.

conceptual understanding; secondary mathematics; assessment; concept map; social network analysis

G420

：A

：1004–9894（2015）03–0055–05

[责任编校：陈隽]

2015–01–09

教育部人文社会科学研究规划基金项目——我国农村中小学教师的TPACK及其教学表现研究（14YJA880054）；南京师范大学人文社会科学青年科研人才培育基金项目——职前教师学科知识的调查研究（14QNPY01）

金海月（1982—），女，江苏海安人，博士，讲师，主要从事数学课程与教学论及教育测量与评价研究．