具有广泛学习策略的回溯搜索优化算法

李牧东，赵 辉，翁兴伟

（空军工程大学航空航天工程学院，陕西西安710038）

具有广泛学习策略的回溯搜索优化算法

李牧东，赵 辉，翁兴伟

（空军工程大学航空航天工程学院，陕西西安710038）

回溯搜索优化算法（backtracking search optimization algorithm，BSA）是一种新型的进化算法。同其他进化算法类似，该算法仍存在收敛速度较慢的缺点。针对这一问题，在详细分析该算法原理的基础上，提出了具有广泛学习策略的改进算法。为了充分利用种群搜索到的较优位置，该策略首先利用提出的最优学习进化方程，通过与引入的随机进化方程之间随机选择来提高算法的收敛速度和搜索精度；另一方面，该策略利用提出的最优学习搜索方程，通过控制种群的搜索方向，促使种群尽快收敛至全局最优解。最后对20个复杂测试函数进行了仿真实验，并与其他3种目前流行的算法进行了比较，统计结果和Wilcoxon符号秩检验结果均表明，所提出的改进算法在收敛速度以及搜索精度方面具有明显优势。

回溯搜索优化算法；广泛学习策略；Wilcoxon符号秩检验；函数优化

0 引 言

在过去的二十年中，元启发式优化算法以其结构简单、求解效率高等特点得到了前所未有的发展，例如众所周知的遗传算法（genetic algorithm，GA）［1］，蚁群算法（ant colony optimization，ACO）［2］和粒子群算法（particle swarm optimization，PSO）［3］等，并在网络优化、智能识别、图像处理以及多目标优化处理等众多领域都得到了广泛的应用。然而，随着多模态、高维、非线性优化问题的出现，对全局优化算法提出了更大的挑战。对此，学者们在对现有元启发式优化技术研究的基础上，提出了大量的改进算法以及新的优化算法，以期提高算法的优化性能。文献［4］通过利用PSO算法搜索过程中粒子的较优解，对搜索方程加以改进，提高了算法的收敛速度；文献［5］通过模拟生物的进化模型提出了差分进化（differential evolution，DE）算法；文献［6］在DE算法的基础上通过引入自适应进化策略提高了算法的性能；文献［7- 9］通过模拟生物的觅食行为分别提出了人工蜂群（artificial bee colony，ABC）算法、布谷鸟搜索（cuckoo search，CK）算法以及森林狼（grey wolf optimize，GWO）算法等新型元启发式优化算法。

回溯搜索优化算法（backtracking search optimization algorithm，BSA）是Cicicioglu于2013年提出的一种新的进化算法［10］。不同于其他进化算法，该算法通过产生实验种群并控制搜索方向和搜索边界大大提高了算法的优化效率，同时，由于该算法仅有一个控制参数，因此操作更加简单。文献［10］通过对不同类型测试函数的仿真实验，证明了该算法具有较好的优化性能。

但是，由于BSA在优化过程中需要对函数进行足够多次数的评价，算法才会逐渐收敛，因此算法消耗较大，同时存在收敛速度慢的缺点。针对这一问题，本文提出了一种新的改进BSA。受文献［11- 12］的启发，首先利用种群当前最优解和较优解信息，提出了广泛学习策略，并在此基础上对算法中的差分进化策略加以改进；其次，为了进一步提高算法的收敛速度，对BSA产生的新种群进行最优学习操作，从而使种群中的个体尽快跳出局部最优点。仿真实验表明该算法能够有效地提高优化性能和效率，是一种可行的优化算法。

1 BSA

BSA是一种基于种群的进化算法，该算法同其他进化算法类似，共分为5个步骤，分别为种群初始化、历史种群设置、种群进化、种群交叉和选择。

（1）种群初始化

由于BSA的性能受种群初始值影响很小，故在该算法中采用随机产生种群的方法进行初始化，即

式中，Pop为种群，i∈［1，2，3，…，N］且j∈［1，2，3，…，D］，N是种群个数，D是种群维数；low和up分别为搜索区间的下界和上界；U是随机均匀分布函数。

（2）历史种群设置

在BSA中，通过设置历史种群OPop来计算搜索方向，按照式（1）对其进行初始化。在算法循环开始时，当随机数a小于随机数b时，OPop＝Pop并将OPop中种群的位置进行随机排列。通过对历史种群的这一操作实现了该算法对种群位置的记忆功能。

（3）种群进化

通过式（2）产生新的种群：

式中，F为控制搜索方向矩阵（OPop－Pop）幅度的参数，且Fi＝3·rand，i∈［1，2，…，N］，rand是［0，1］的随机数。

（4）种群交叉

BSA提出了一种新的种群交叉策略，通过设置混合比例参数来控制种群间交叉的粒子个数，具体公式如下：

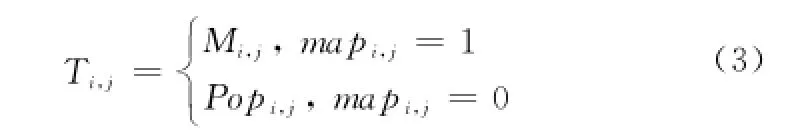
式中，map为N×D的二元整数矩阵，初始赋值为1，具体计算公式如下：

式中，randi（D）为从［0，D］中随机取一个整数，mr为混合比例参数，且mr＝1；rand，a，b为［0，1］的随机数；u为随机排序后且u∈［1，2，3，…，D］的整数向量。不同于DE算法的交叉策略，BSA通过利用mr·rand·D和randi（D）有效控制了新种群T中元素的个数，当a＜b时，mapi为多个具有随机位置的二元向量；反之，mapi为仅有一个元素为0的二元向量。

在新种群产生后，对种群中的元素进行边界控制，若种群中的元素超出搜索边界，则按式（1）产生新的种群。

（5）选择

通过贪婪选择机制在新种群T与初始种群Pop中选择适应度值较好的种群个体，并记录当前最优解和对应的解向量，同时更新初始种群，完成一次迭代。重复上述过程，直到满足循环终止条件，最后输出最优解。

2 具有广泛学习策略的BSA改进算法

通过对BSA的原理分析可知，该算法在循环初期具有较好的探索能力，然而随着迭代次数的增多，BSA容易陷入局部最优，导致算法收敛速度减慢，对于较复杂的多峰函数，存在无法搜索到最优值的缺点。另一方面，BSA中仅仅通过设置历史种群对种群的搜索方向加以控制，这也是导致其收敛速度减慢的原因。对此，本文提出了广泛学习策略，通过学习种群当前搜索到的最优信息来控制算法的搜索方向，具体包括最优学习进化方程和最优学习搜索方程；另一方面，考虑到保持BSA的探索能力，改进算法设置了两种不同的进化方程，具体改进如下。

2.1 最优学习进化方程

文献［11］在研究现有DE算法进化策略的基础上，提出了一种新的进化策略，即“DE／current-to-gr_best／1”进化搜索策略，如式（5）所示。该策略通过从当前种群选取的p%个种群个体中选出较优的个体作为控制算法搜索方向的控制向量，有效地提高了算法的收敛速度。

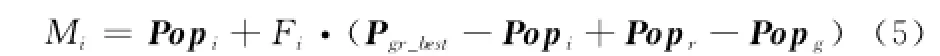
式中，Pgr_best为选取的较优个体，i，r，g∈［1，2，3，…，N］且它们之间互不相等。同时文献［4］提出了利用种群当前最优解信息的方法改善了PSO算法的优化性能。本文在文献［11］的基础上，通过充分学习种群个体当前搜索到的最优信息，对式（5）加以改进，提出了最优学习进化方程：

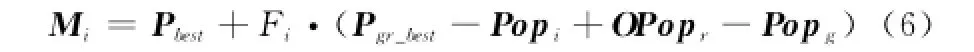
式中，Pbest为当前种群搜索到的最优位置；OPop是历史记录种群。同时为了避免算法陷入局部最优，本文引入“DE／rand／2”进化策略：

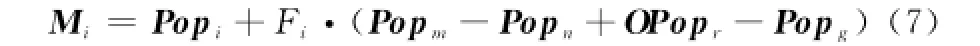
式中，i，m，n，r，g∈［1，2，3，…，N］且它们之间互不相等；OPop是历史记录种群。通过随机选择式（6）和式（7）平衡算法的探索与开发能力。

2.2 最优学习搜索方程

文献［12］针对ABC算法收敛速度慢、搜索精度不高的问题，受到文献［4］的启发，提出了最优引导搜索方程，改善了ABC算法的优化性能：

式中，φi，j和μi，j分别为［－1，1］和［0，1.5］的随机数；Popbest，j为当前最优解向量的第j维。

考虑到种群在完成最优学习随机差分进化操作之后，种群需要对搜索空间进一步搜索，以期快速搜索到全局最优解，因此在式（8）的基础上提出了最优学习搜索方程：

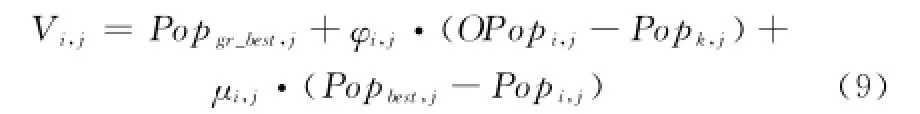
式中，Popgr_best是从更新后的Pop种群中随机选取p%后，选出较优的种群个体作为进一步搜索的方向引导向量；OPop是历史记录种群。该方程在式（8）的基础上，进一步提高了方程的开发能力，对快速收敛至全局最优解具有明显作用。

2.3 改进算法流程

由于BSA存在收敛速度慢，容易陷入局部最优的缺点，结合本文提出的最优学习策略，提出了一种新的BSA改进算法。该算法首先通过随机选择两种不同的随机进化方程，分别为“DE／rand／2”和本文提出的最优学习进化方程，对种群进行初始搜索；随后对优化后的种群采用最优学习搜索方程进行进一步的优化操作，使其快速跳出局部最优，提高其收敛速度。下面给出了BSA改进算法的流程：

（1）种群初始化

（2）while不满足算法终止条件do

（3） for i＝1 to N do

（4） if rand＜rand do

（5） mapi，u（1∶｜mr·rand·D｜）＝0

（6）Mi＝Pbest＋（mapi·Fi）·（Pgr_best－Popi＋OPopr－Popg）

（7） else do

（8） mapi，randi（D）＝0

（9）Mi＝Popi＋（mapi·Fi）·（Popm－Popn＋OPopr－Popg）

（10） end if

（11） end for

（12）贪婪选择机制选出较优的解并更新Pop

（13） for i from 1 to N

（14） 利用式（9）产生新的优化种群V

（15） end for

（16）贪婪选择机制选出较优的解并更新Pop

（17）end while

（18）输出最优值和最优解向量

3 仿真实验

为了验证本文提出的BSA改进算法（后简称CLBSA）的有效性，对CEC 2005［12］中的20个复杂实数优化问题进行了测试仿真，同时与标准BSA、文献［4］提出的CLPSO算法以及文献［6］提出的DE改进算法SADE进行了比较。其中F1～F5为单模函数，F6～F12为标准多模函数，F13～F14为扩展的多模函数，F15～F20是具有混合结构的复杂函数。相比于一般的测试函数，CEC 2005中所用到的测试函数能较好地测试算法的优化性能，表1给出了20个函数的基本信息，包括函数名称、搜索区间、函数维数以及最优值，其他关于函数的详细描述可以参见文献［12］。在仿真中，设置种群个数为30，最大评价次数为150 000，算法精度GolErr＝1e－14（即优化得到的全局最优值与理论最优值差的绝对值小于GolErr或者达到最大评价次数时，算法终止）在BSA和CLBSA中，控制参数mr＝1，p%＝20%；其他两种比较算法按照文献［4］和文献［6］的参数设置方法进行设置。

表1 20个测试函数的基本描述

本文采用Matlab R2013a进行仿真，运行环境为Intel（R）Core（TM）i5- 3470处理器，3．46G内存。仿真针对同一测试函数，每个算法独立运行30次，比较了4种算法对20个测试函数的统计平均值和方差。另外，为了更好地对实验结果进行分析，本文引入了文献［13］采用的优化算法比较分析方法，即Wilcoxon符号秩检验。该检验方法是一种成对比较方法，能够有效检验出不同算法存在的明显差异。在本文中通过将CLBSA分别与其他算法分别比较得出统计数据，其中，将30次独立运行的最优值作为算法间比较的样本数据，信息显著水平设置为0．05。

表2给出了4种算法在20种测试函数下基于30次独立运行的统计平均值（Mean）和方差（Std）。从表2中可以看出，CLBSA无论从收敛精度还是算法稳定性方面，相比于BSA，除了在函数F1，F3，F13和F16外，均有明显提高，其中在函数F1的优化方面，CLBSA和BSA性能相当。相比于CLPSO算法，可以看出，除了函数F1，F7外，CLBSA在收敛精度和算法稳定性方面均优于CLPSO算法，其中，对F1函数的优化表现出相当的性能，在函数F7的优化方面，CLBSA在收敛精度方面与CLPSO算法相当，但算法稳定性优于CLPSO算法。相比于SADE算法，CLBSA除了函数F1，F4，F5和F7，均表现出了明显较优的优化性能，其中在函数F1，F4和F7优化中，CLBSA表现出了较优的稳定性。

表2 4种算法对20种测试函数的测试结果

图1 4种不同算法关于8个测试函数随函数评价次数变化的收敛曲线

为了进一步说明CLBSA算法的有效性，图1给出了4种算法的收敛曲线。由于篇幅限制，本文列出了典型的8种测试函数的收敛曲线。从图1中可以看出，相比于BSA、 CLPSO算法，本文的改进算法具有明显较快的收敛速度；相比于SADE算法，本文算法除对函数F1和F9的收敛过程略差外，对于其他函数的收敛过程均优于SADE算法。

为了更加清楚地比较4种算法的优化性能，表3给出了Wilcoxon符号秩检验的检验结果。其中“R＋”表示CLBSA样本数据中优于其他算法的符号数；“R－”表示不如其相比较算法的符号数；“＋”表示假设不成立（两种算法存在明显差异），CLBSA表现出更好的性能；“－”表示假设不成立（两种算法存在明显差异），CLBSA表现出较差的性能；“＝”表示假设成立，即两种算法没有较大差异。各统计值的具体计算原理可参见文献［13］。从表3中可以看出，相比于CLPSO算法，本文算法仅对F1函数优化中与其性能并无明显差异，而在其他函数的优化方面明显优于CLPSO算法；相比于SADE算法，在函数F1、F2和F7的优化过程中，本文算法与其并无明显差异，在函数F16的优化中，SADE算法优于本文算法，而在其他函数的优化方面，本文算法表现出了明显优于SADE算法的优化性能；相比于BSA算法，在F3、F15、F16和F18的优化过程中，性能优于本文算法，在函数F1和F2的优化中，本文算法与其优化性能相当，而对于其他函数的优化方面，本文算法表现出明显优于BSA的性能。因此，相比于其他3种算法，CLBSA在对CEC 2005中的20个测试函数的试验结果可以说明其改进的有效性。

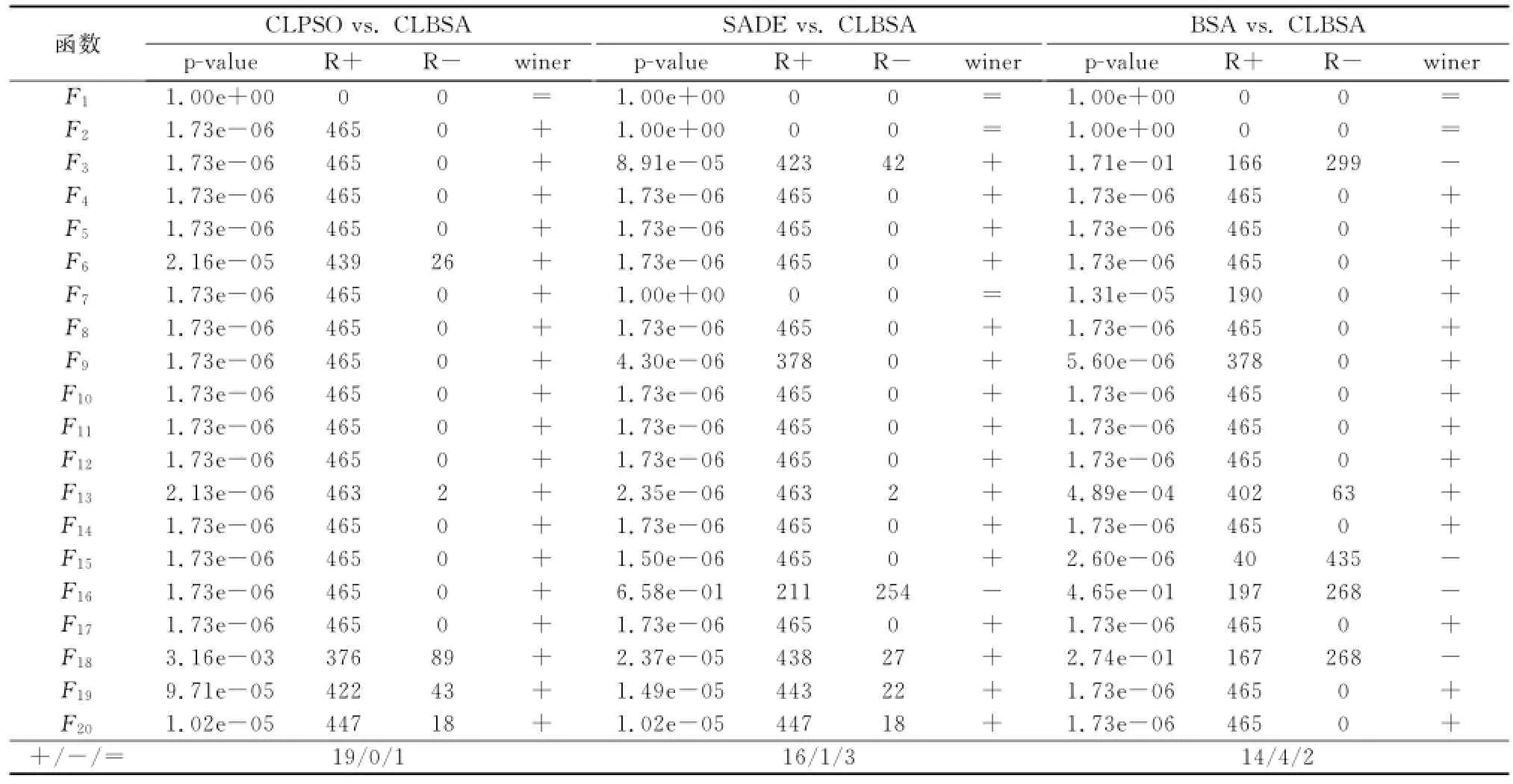
表3 基于30次独立运行的20个测试函数最优值双边Wilcoxon符号秩检验结果

4 结 论

为了解决标准BSA收敛速度慢和搜索精度不高的问题，本文提出了基于广泛学习策略的改进算法，该策略主要由最优学习进化方程和最优学习搜索方程组成，实现了对BSA两部分的改进。通过对CEC 2005中20个复杂测试函数的统计结果和Wilcoxon符号秩检验结果可以看出，相比于其他3种优化算法，本文提出的BSA改进算法有效提高了算法的搜索性能，是一种提高BSA收敛速度的可行解决方案。

另一方面，如何利用改进的优化算法解决多目标优化问题以及动态优化问题是下一步需要研究的方向。

［1］Holland J．Adaptation in natural and artificial systems［M］．Cambridge，MA：MIT Press，1992．

［2］Dorigo M，Stutzle T．Ant colony optimization［M］．Cambridge，MA：MIT Press，2004．

［3］Kennedy J，Eberhart R．Particle swarm optimization［C］∥Proc. of the IEEE International Conference on Neural Networks，1995：1942- 1948.

［4］Liang J J，Qin A K，Suganthan P N，et al．Comprehensive learning particle swarm optimizer for global optimization of multimodal functions［J］.IEEE Trans.on Evolutionary Computation，2006，10（3）：281- 295.

［5］Price K V，Storn R，Lampinen J．Differential evolution：a practical approach to global optimization［M］．Berlin：Springer Press，2005．

［6］Zhang J Q，Sanderson A C．SADE：adaptive differential evolution with optional external archive［J］.IEEE Trans.on Evolutionary Computation，2009，13（5）：945- 958.

［7］Karaboga D，Akay B．A comparative study of artificial bee colony algorithm［J］.Applied Mathematics and Computation，2009，214（12）：108- 132.

［8］Yang X S，Deb S．Cuckoo search via levy flights［C］∥Proc.of the World Congress on Nature and Biologically Inspired Computing，2009：210- 214.

［9］Seyedali M，Seyed M M，Andrew L．Grey wolf optimizer［J］. Advances in Engineering Software，2014，69：46- 61.

［10］Pinar C．Backtracking search optimization algorithm for numerical optimization problems［J］.Applied Mathematics and Computation，2013，219（15）：8121- 8144.

［11］Minhazul I S，Das S，Ghosh S，et al．An adaptive differential evolution algorithm with novel mutation and crossover strategies for global numerical optimization［J］.IEEE Trans.on Systems，Man，and Cybernetics—Part B：Cybernetics，2012，42（2）：482- 500.

［12］Suganthan P N，Hansen N，Liang J J，et al．Problem definitions and evaluation criteria for the CEC 2005 special session on real-parameter optimization［R］．Singapore：Nanyang Technological University，2005．

［13］Derrac J，Garcia S，Molina D，et al．A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms［J］. Swarm Evolution Computation，2011，1（1）：3- 18.

Backtracking search optimization algorithm with comprehensive learning strategy

LI Mu-dong，ZHAO Hui，WENG Xing-wei
（School of Aeronautics and Astronautics，Air Force Engineering University，Xi’an 710038，China）

The backtracking search optimization algorithm（BSA）is a novel evolution algorithm．However，the BSA has the problem of low convergence speed as the same as the other evolution algorithms．Aiming at this problem，an improved BSA with the comprehensive learning strategy is proposed based on detailed analysis of BSA．The strategy is used for making full use of the better solutions that the population obtains．Firstly，the global best learning equation is proposed and the random evolution equation is introduced in the strategy．They are chosen randomly so as to improve the convergence speed and precision of the improved algorithm．Secondly，in order to control the search direction，the global best search equation is proposed in the strategy so as to reach the global best solution as fast as possible．Finally，20 complex benchmarks and other three popular algorithms are compared to illustrate the superiority of BSA with comprehensive learning strategy．The experimental results and the Wilcoxon signed ranks test results show that the BSA with comprehensive learning strategy outperformed the other three algorithms in terms of convergence speed and precision．

backtracking search optimization algorithm（BSA）；comprehensive learning strategy；Wilcoxon signed ranks test；function optimization

TP 13

A

10．3969／j．issn．1001-506X．2015．04．36

李牧东（1987-），男，博士研究生，主要研究方向为最优化理论与方法、无人飞行器武器系统总体技术。E-mail：lmd422＠163．com

1001-506X（2015）04-0958-06

2014- 05- 13；

2014- 09- 25；网络优先出版日期：2014- 11- 05。

网络优先出版地址：http：／／w ww．cnki．net／kcms／detail／11．2422．TN．20141105．1633．011．html

航空科学基金（20105169016）；中国博士后基金（2012M5211807）资助课题

赵 辉（1974-），男，教授，博士，主要研究方向为武器系统与运用工程、最优化方法。E-mail：zhao_kgy＠163．com

翁兴伟（1980-），男，副教授，博士，主要研究方向为武器系统与运用工程、最优化方法。E-mail：liuziyang_kgy＠163．com